利用初等函数求解BISHOP法

史建芳

(忻州师范学院 五寨分院,山西 忻州 036200)

利用初等函数求解BISHOP法

史建芳

(忻州师范学院 五寨分院,山西 忻州 036200)

BISHOP法求解边坡问题是被广泛使用的一种方法，但是传统的BISHOP法是连加数学模型，在施工工程中计算量较大、计算精度降低,不利于工程实际中的使用。初等函数是分析学中最为常见的函数，工程人员使用较为简单的设备便可以计算。针对传统BISHOP法的连加数学模型，利用微分工具将其转化为初等函数的形式，并根据初等函数的相关性质，探究BISHOP法边坡问题的数理关系，从而有效地避免传统BISHOP法浩繁的计算量和函数发散的风险。

初等函数；连加数学模型；积分形式；BISHOP法

BISHOP法是边坡分析中的经典算法[1]，相较于Fellenius法、Janbu法、Sarma法、Morgenstern & Price法、Spencer法。BISHOP法的计算精度更高、计算思路更加清晰，被认为是计算边坡问题的最优方法，也代表了边坡问题最小安全系数的正确解。

但是，传统BISHOP法是连加数学模型，在计算的时候，需要对边坡进行分块，然后逐次累加，在累加的基础上，再进行滑弧的遍历。如此一来，计算量便十分浩繁[2]。同时，由于分块对于精度有着不可忽视的影响，导致传统BISHOP法在精度上不能精确。相关研究学者试图利用初等函数对传统的BISHOP法进行改进，这些改进是建立在新的假设的基础上，由于这些新的假设并不符合工程实际，其计算方法也较为复杂，导致改进后的BISHOP法计算复杂度反而增加，降低了计算效率[3]。

本文针对传统意义上的BISHOP法，利用数学上的微分工具，将传统BISHOP法的连加数学模型转化为用初等函数表示的积分数学模型。对初等函数进行分析，探究BISHOP法边坡问题数理上的相关隐含规律[4]。

1 传统BISHOP法的数学模型

1.1 传统BISHOP法数学模型的构建

图1是传统BISHOP法的土条分块示意图，其中，每一个土条的编号为i；i号土条下端滑弧的长度为li；i号土条的重量为Wi；i号土条下端滑弧中点的法线与圆心的夹角为θi，θi可为正也可以为负；滑弧所在的圆心为点O；滑弧的半径为R；为作用在土条滑弧上的抗剪力；为作用在土条滑弧上的有效法向反力；uili为孔隙水压力；Ei为土条左侧侧的法向力；Ei+1为土条右侧侧的法向力。

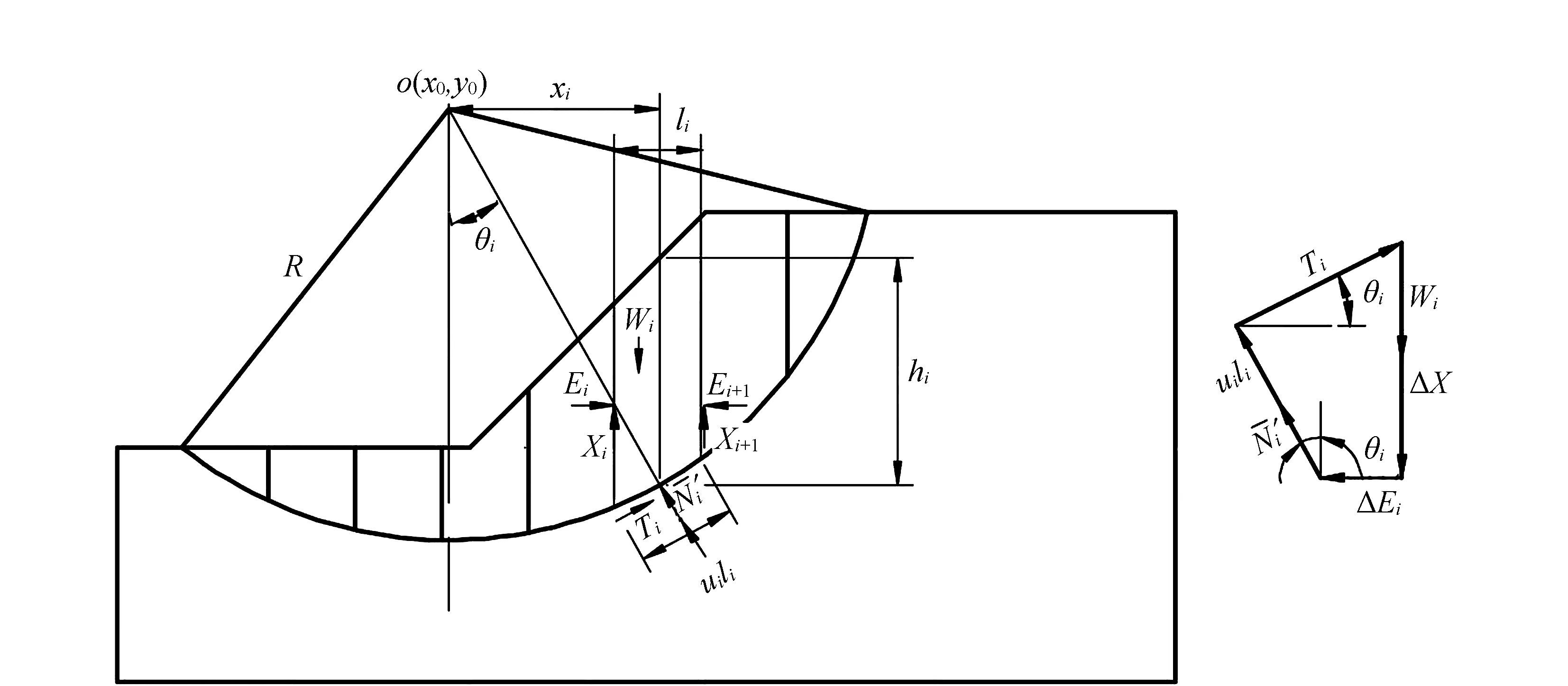
图1 传统数学模型

在土条的竖直方向，有

(1)

抗剪力为

(2)

可以表示为

(3)

其中

(4)

因为对圆心存在力矩平衡，故而

R.

(5)

联立式(2)、式(3)、式(4)、式(5)，得到

(6)

令ΔXi均为0，有

(7)

因为

ui=γhiB,

(8)

式(7)可以写成

(9)

式中：γ为重度[5]。

1.2 传统BISHOP法数学模型的缺点

传统连加数学模型是基于土条划分的，土条划分的情况必然会对最终结果造成影响[6]。以文献[15]为例：均质土坡的坡高H=50m，重度γ=20kN/m3，坡比tanα=1∶3.25，内摩擦角tanφ=0.2，黏聚力c=60kPa。先根据不同的分条数量N，分别进行最小安全系数Ks的求解，绘制图形如图2所示。

图2 分条数量N对最小安全系数的影响

根据图2，当N=3时，Ks≈1.705；当N=45时，Ks≈1.365，误差高达25%。说明传统BISHOP的连加数学模型对土条划分条数N有着很强的依赖性[7]。

2 基于初等函数的BISHOP积分形式求解

图3中，H是坡高；O是坐标原点，坡脚在其右上方处，水平距离为1.5H，竖直距离为H；O′是滑弧的圆心，R为滑弧的半径；α为坡角；区域D为坡底、坡面和坡顶与滑弧所围成区域；黑色条带部分为土条；i是土条的编号；θi是第i号土条的底面中点的法线与铅垂线的夹角，若θi位于铅垂线的左边则为负；若θi位于铅垂线的右边则为正[8]。

图3 计算坐标系

图4中，dσ是微分单元，θ是dσ的底部中点的法线与铅垂线的夹角。根据图4，可以将滑弧的方程写作：

(x-x0)2+(y-y0)2=R2.

(10)

对于θ，有

(11)

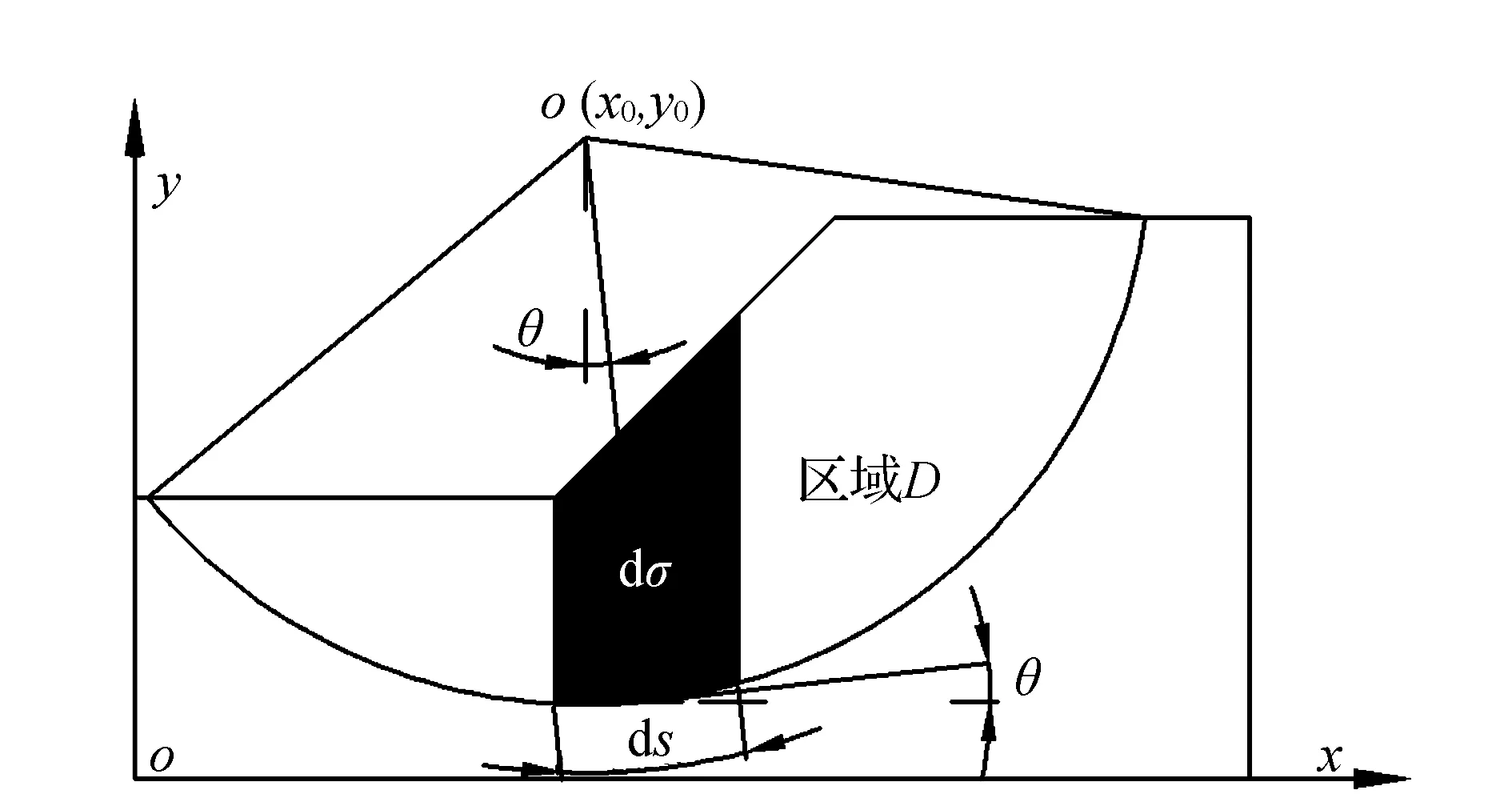
图4 土坡微分形式

所以，θ的正弦和余弦可以表示为

(12)

所以，

(13)

其中：f(x)是坡面函数：

(14)

∑Wisinθi可写作

∑Wisinθi=

x.

(15)

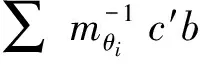
x.

(16)

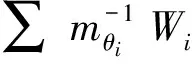
x.

(17)

联立式(13)、式(14)、式(15)、式(16)、式(17)，得到BISHOP法的积分形式

(18)

其中，

(19)

x.

(20)

将式(18)写成显函数的形式

其中，

(22)

至此，利用初等函数建立了安全系数K的表达式。

3 结果分析

3.1 计算精度

参考[9]的算例：一均质土坡，坡高H=50m，重度γ=19.62kN/m3，内摩擦角tanφ=0.2 ，黏聚力c=58.86kPa。坡比取1∶2.25，1∶2.50，1∶2.75，1∶3.00及1∶3.25共5种情形，分别使用瑞典法、传统BISHOP方法(传统连加数学模型)、基于初等函数的BISHOP法(积分数学模型)进行计算，结果列于表1。

表1 不同坡比下的安全系数

通过表1可以看出：边坡安全系数的半解析BISHOP法是传统BISHOP法的下限解，半解析BISHOP法所得安全系数为传统BISHOP法所得安全系数的96%～99%。无论是半解析BISHOP法还是传统BISHOP法，其所得安全系数均比瑞典法所得安全系数要大，这与实际是相符的。

3.2 计算效率

某均质土坡如图 2 所示，其中，坡高H=19m；坡角α=45°；重度γ=19.62kN/m3；黏聚力c=40kPa；摩擦角φ=18°。通过计算分别得出强度折减法、传统BISHOP法、半解析BISHOP方法计算边坡最小安全系数Ks和计算时间(见表2)。

表2 不同计算方法所得到的安全系数与计算耗时

根据表2，半解析BISHOP法所得结果非常合理且比强度折减法和传统BISHOP法都精确[12-14]。此外，传统BISHOP法计算量浩大，计算耗时约为强度折减法的1.5倍。但半解析BISHOP法因其算法简明，故对计算机内存、CPU的占用率以及耗时极少。半解析BISHOP法的耗时约为强度折减法的5%，约为1.3%。

3.3 参数对于安全系数的影响

以文献[15]为例，均质土坡的坡高H=50m，重度γ=20kN/m3，坡比tanα=1:3.25，内摩擦角tanφ=0.2，粘聚力c=60kPa。利用式(21)、式(22)可知，最危险滑弧的位置

(23)

1)坡高的影响。取H=40m、45m、55m、60m，其余参数不变，利用式(21)、式(22)可知最危险滑弧的位置，如表3所示。

表3 坡高的影响

其余参数不变的情况下，H越大，K越小，x0,y0,R的值越大。

2)坡角的影响。取tanα=1∶4.25、1∶3.75、1∶2.75、1∶2.25，其余参数不变，利用式(21)、式(22)可知最危险滑弧的位置,如表4所示。

其余参数不变的情况下，α越大，K,x0,y0,R越小。

3)重度的影响。取γ=18kN/m3、19kN/m3、21kN/m3、22kN/m3，其余参数不变，利用式(21)、式(22)可知最危险滑弧的位置，如表5所示。

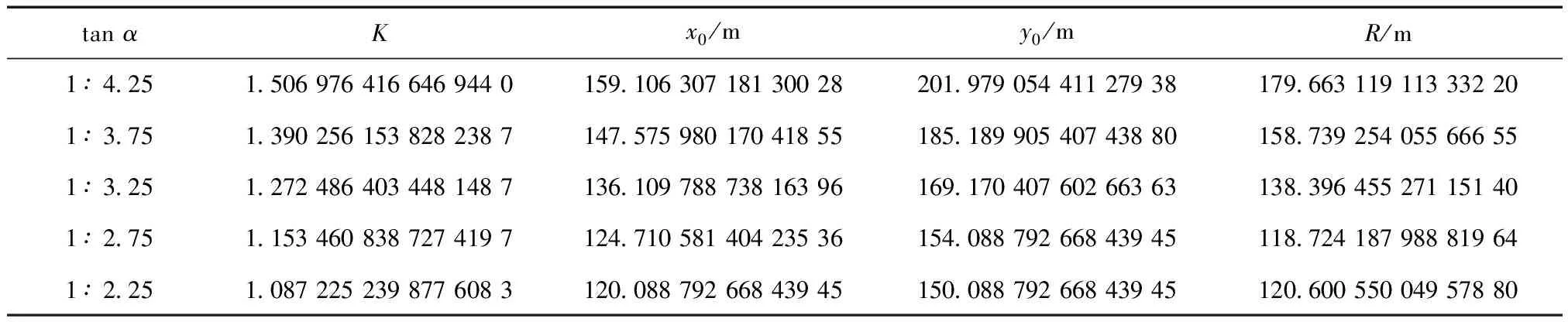
表4 坡角的影响

表5 坡高的影响

其余参数不变的情况下，γ越大，K,x0越小，y0,R越大。

4)内摩擦角的影响。取tanφ=0.1、0.15 、0.25、0.3，其余参数不变，利用式(21)、式(22)可知最危险滑弧的位置,如表6所示。

表6 内摩擦角的影响

其余参数不变的情况下，φ越大，K,y0,R越大，x0的值越小。

5)粘聚力的影响。取c=50kPa、55kPa、65kPa、70kPa，其余参数不变，利用式(21)、式(22)可知最危险滑弧的位置，如表7所示。

表7 粘聚力的影响

其余参数不变的情况下，c越大，K,x0越大，y0,R的值越小。

4 结 论

利用初等函数求解BISHOP，得出以下结论：

1)基于初等函数的BISHOP积分模型的计算精度远远大于传统连加数学模型；

2)基于初等函数的BISHOP积分模型的计算速度远远大于其他边坡安全系数计算方法；

3)其余参数不变的情况下，H越大，K越小，x0,y0,R的值越大；

4)其余参数不变的情况下，α越大，K，x0，y0，R越小；

5)其余参数不变的情况下，γ越大，K，x0越小，y0，R越大；

6)其余参数不变的情况下，φ越大，K，y0，R越大，x0的值越小；

7)其余参数不变的情况下，c越大，K，x0越大，y0，R的值越小。

[1] 王俊奇, 李闯, 董晔.Bishop法的半解析解及其广义数学模型[J]. 水利与建筑工程学报, 2015(6):123-128.

[2] 段双安. 初等函数值域研究[D]. 西安：西北大学, 2015.

[3] 王学成. 应用导数求函数参数范围[J]. 理科考试研究(高中版), 2016, 23(4):12-12.

[4] 刘纪陆, 刘苏红,LIUJi-lu,等. 利用插值函数求解基础隔震结构的地震响应[J]. 建筑技术, 2016(5).

[5] 刘纪陆, 刘苏红. 利用插值函数求解剪力墙结构的地震响应[J]. 四川建筑科学研究, 2015, 41(5):79-83.

[6] 张敏. 利用构造函数法求解不等式问题[J]. 中学教学参考, 2016(17).

[7] 孙卫卫. 多元函数极值的初等变换求解法[J]. 长沙大学学报, 2015(5):4-5.

[8] 孙娟, 张引娣, 刘奋进. 线性随机微分方程的函数分离求解法[J]. 赤峰学院学报(自然科学版), 2016, 32(7).

[9] 蒋斌松，康伟. 边坡稳定性中BISHOP法的解析计算[J]. 中国矿业大学学报,2008，37(3)：287-290.

[10] 赵张超.胡艳红，徐延新.QVIP的广义间隙和误差界[J].黑龙江工程学院学报，2016，30(2)：46-48.

[11] 经中进. 一道无理函数值域求解方法纵横谈[J].中学生数理化(学研版), 2015(1):16-16.

[12] 张鲁渝,郑颖人. 简化Bishop法的扩展及其在非圆弧滑面中的应用[J]. 岩土力学， 2004(6).

[13] 李亮,杨小礼,禇雪松,等. 基于Bishop法假定的边坡临界滑动场方法及应用[J]. 中南大学学报(自然科学版)，2011(9).

[14] 王军,谢桂华,李继祥. 边坡稳定性分析的广义Bishop法[J]. 江苏科技大学学报(自然科学版)，2009(4).

[15] 张天宝.土地稳定分析圆弧法的数值研究[J].成都工学院学报，1978(1)：97-122.

[责任编辑：郝丽英]

A method of BISHOP based on elementary fanctions

SHI Jianfang

(Wuzhai Sorting of Shanxi Province,Xinzhou teachers college,Xinzhou 036200,China)

BISHOP method is a kind ofwidely used method to solve the slope problem, but the traditional BISHOP method is a coupled mathematical mode, in the construction project, the computation is large and the precision of calculation is reduced, it doesn’t use into the actual project. The elementary function is the most common function in the analysis, in practical engineering, the engineering personnel can be calculated by using a relatively simple device. This paper?aimed at the coupled mathematical model of traditional BISHOP method, using differential tools to transform it into the form of elementary functions, and according to the correlation property of elementary function, explore the mathematical relation of BISHOP method of slope problems, in order to avoid large calculation of traditional BISHOP method and the risk of divergence of function.

elementary function; coupled mathematical model; integral form; BISHOP method

10.19352/j.cnki.issn1671-4679.2016.06.012

2016-07-05

史建芳(1982-)，女，讲师，研究方向:初等数学函数的值域.

O174

A

1671-4679(2016)06-0049-06