基于免疫-细菌觅食算法的旅游线路选择问题研究

贾润亮

(山西省财政税务专科学校 信息学院，山西 太原 030024)

基于免疫-细菌觅食算法的旅游线路选择问题研究

贾润亮

(山西省财政税务专科学校 信息学院，山西 太原 030024)

针对旅游行业迅猛发展的态势，对旅游路线选择问题进行抽象、概化，将旅游路线选择问题转化为特定条件下数学方程最优化问题。结合免疫算法和细菌觅食算法融合半解析解的思想，构建一种全新的优化算法——免疫细菌觅食算法(Generate Bacterial Foraging Algorithm，GBFA)，对旅游路线选择问题进行求解，对几种线路的旅游花费、游玩时间等方面进行比较。结果显示：GBFA在计算效率上远远高于其他方法，路线花费更低、游玩时间更多、交通时间与等待时间更短、游客休息时间更充裕，说明该方法计算结果更加精确，计算流程更加优化。

路径选择；等待时间；GBFA；旅游线路；期望花费

目前，社会旅游成为人们消遣的一种重要方式[1]。如何在现有的成本下游览更多的景点，体验更加友好的旅行观感，进而提升旅游的性价比是国内外学者广泛关注的问题。但是，旅行线路规划问题涉及到很强的非线性，现有解法多难以收敛[2-3]。鉴于此，国内外学者对RA网络的多协同排序算法进行了大量研究。SINGH、WU Guang等人[4-5]将旅游花费和游览的景点进行加权，进而构造满足度函数，基于遗传算法对旅游线路规划问题进行求解，得到在满足游览时间限定和经费预算的局部最优解，但是文献[4]和文献[5]无法适应跨时区的旅游路线，仅限于小范围求解。Huiping Liu等人[6]基于蚁群算法对旅游路径选择问题进行求解，充分考虑了景点的自身特性，譬如营业时间、门票价格问题，文献[6]所使用的蚁群算法容易陷入局部最优解，其全局搜索能力和收敛速度、求解精度欠佳。Nuengwong[7]、Dennerline[8]等人基于Priceline多年的旅游数据，建立起基于旅客自身消费习惯的路线规划数学模型，并利用蜂群算法求解具有限定条件的数学方程，得到的结果更加人性化、更加容易满足旅客的消费心理，但是文献[7]和文献[8]所使用数据过于繁杂，计算量过大，而且在计算时容易产生数值耗散。侯乐等人[9]首先根据相关目标和约束采用ILS算法求解旅游景点及初始旅游线路，然后在满足旅游景点时间窗约束及景点总数不变的情况下采用CS算法进一步最小化旅游线路的时间花费，但是文献[9]所使用方法计算精度较差。

本文在此基础上选用细菌觅食算法(简称BFA)，同时基于免疫算法(generate and test)的相关概念，融合半解析解的相关思想[10]，针对BFA算法的3个操作环节(复制操作环节、趋向性操作环节和迁移操作环节)，提出BFA的一种优化算法GBFA(Generate Bacterial Foraging Algorithm)：将趋向性操作环节中的步长变为非固定步长，可以随着计算的进行而改变，建立趋向性操作步长的动态更新机制；此后，利用免疫算法(generate and test)替换BFA的复制操作环节，针对细菌群落进行筛选，将其中适应度较高的细菌复制并替换适应度较低的细菌；最后，在迁移操作环节中，适应度最高的个体被驱散的概率为0，适应度最高的个体被驱散的概率为Ped。利用该算法对旅游路线选择问题进行求解，充分考虑跨时区旅游的时差问题，找到景点之后的等待问题、交通耗时问题以及餐饮花费问题。并同当前常用的几种路线选择方法进行比较，以验证本文所提出方法的优越性和适用性。

1 问题描述

为了更好地用数学模型对所研究问题进行描述，对模型中所涉及到的符号进行说明。其中，R为旅游路线，R={r1,r2,r3，…}；T为旅游路线对应的旅游时间，min；C为旅游路线R对应的花费，元；Openi为景点i开门的时间；Closei为景点i关门的时间；Timei为游客到达景点i的时间；Waiti为游客提前到达景点i后所需要的等待时间，min；Visiti为可支配的旅游时间，min；Travel为游客可支配的旅游时间，min;budget为游客的费用预算，元。

旅游花费C主要包括交通费用c(eij)、景点的旅游费用c(i)；旅游时间T主要包括到达景点所需要的旅途时间t(eij)、游览景点所需要的时间Visiti、提前到达目的地而需要等待的时间Waiti。具体计算方法如下：

(1)

(2)

(3)

如果两个地点相隔比较远，就需要考虑时差问题

(4)

式中：Ti为第i个地点的时间，Tj为第j个地点的时间，yi为第i个地点的经度，yj为第j个地点的经度。第i个地点到第j个地点的距离Li,j为

Li,j=arccos[sinxisinxjcos(yi-yj)+

cosxicosxj]R.

(5)

式中：R为地球的半径，取6 371.004 km，xi为第i个地点的经度，xj为第j个地点的经度。

定义旅客满意度函数(目标函数)

(6)

式中：ω(R)是权重系数，代表了旅客对花费的在意程度。

根据现实问题，游客旅行所花费的总时间必须小于游客预算时间，游客所花费的钱财必须小于游客的预算花费，游客在每个景点的游玩时间必须小于该景点的营业时间，用数学语言表示为

T≤Travel，

(7)

C≤budget，

(8)

Visiti≤Closei-Openi.

(9)

至此，将旅客旅行路线规划问题变成在有约束情况下数学模型最优化问题。

2 算法简介

为求解在有约束情况下数学模型最优化问题，下面利用GBFA算法进行解答。

2.1 GBFA算法的基本思想

BFA中第i次的步长为

(10)

式中：Ns为BFA虚拟的细菌群落中细菌游动的最大次数；Led为细菌游动的初始步长。细菌移动的每一次步长均小于初始步长Led。并且计算开始之时(i值较小)，第i次的步长Ci很大，可以提高搜索的速度，使得计算可以更快进行；随着计算过程的进行(i值的增大)，第i次的步长Ci会越来越小，这是为了在计算的后期保证足够的收敛精度。

在趋向性操作步长的动态更新机制建立之后，将群落中所有细菌的适应度进行累加，并由从大到小的顺序进行排列，形成细菌序列。将细菌序列前m(m为百分比)部分的细菌进行复制n次，将细菌序列中的其余细菌进行剔除，m和n的关系为

(11)

如此一来，使用细菌群落中m部分的细菌代表了原有的细菌菌落，可以提高细菌群落的整体觅食能力。此后，依照如下步骤对细菌菌落进行变异、繁殖：

1)挑选出细菌群落中适应度较高的细菌，标记为克隆群体A；

2)克隆群体A繁殖成为群体B：

(12)

式中：Round为四舍五入函数；S为细菌群落的整体个数；A(i)为计算的克隆群体A的个数；i为第i次计算；α为克隆的系数。为了方便计算，将适应度F进行标准化

(13)

其中，max为取最大值函数。

3)对群体B进行变异操作，产生群体C：

B(i)=B(i)+βrandomn(C).

(14)

式中：random为随机函数；B(i)为计算的克隆群体B的个数；β为变异概率，计算方法为

β=e-F(n-i+1).

(15)

根据式(6)可知，适应度越高的个体，变异概率β越大。

因为交叉方法

H=B(x1)-B(x2)+B(x3)-B(x4).

(16)

式中：x1，x2，x3，x4为克隆群体A中4个不同的细菌。将群体C融合进入群体B中，形成群体D：

D=B+C.

(17)

4)在群体D中，将其中前m(m为百分比)部分的细菌进行复制n次，将其余细菌进行剔除。

在传统的BFA算法中，需要设定一个迁移概率Ped，如果随机数小于迁移概率Ped，就会对细菌进行迁移操作。这样做的目的是希望细菌可以跃出局部最优解的陷阱。但是，这种做法同样具有极大的弊端，因为迁移概率Ped对于所有的细菌都有效，无论细菌的适应度如何，都可能被迁移。GBFA算法在迁移操作环节中，适应度最高的个体被驱散的概率为0，适应度最高的个体被驱散的概率为Ped，以提高搜索的速度。

根据以上思想，绘制GBFA算法流程如图1所示。

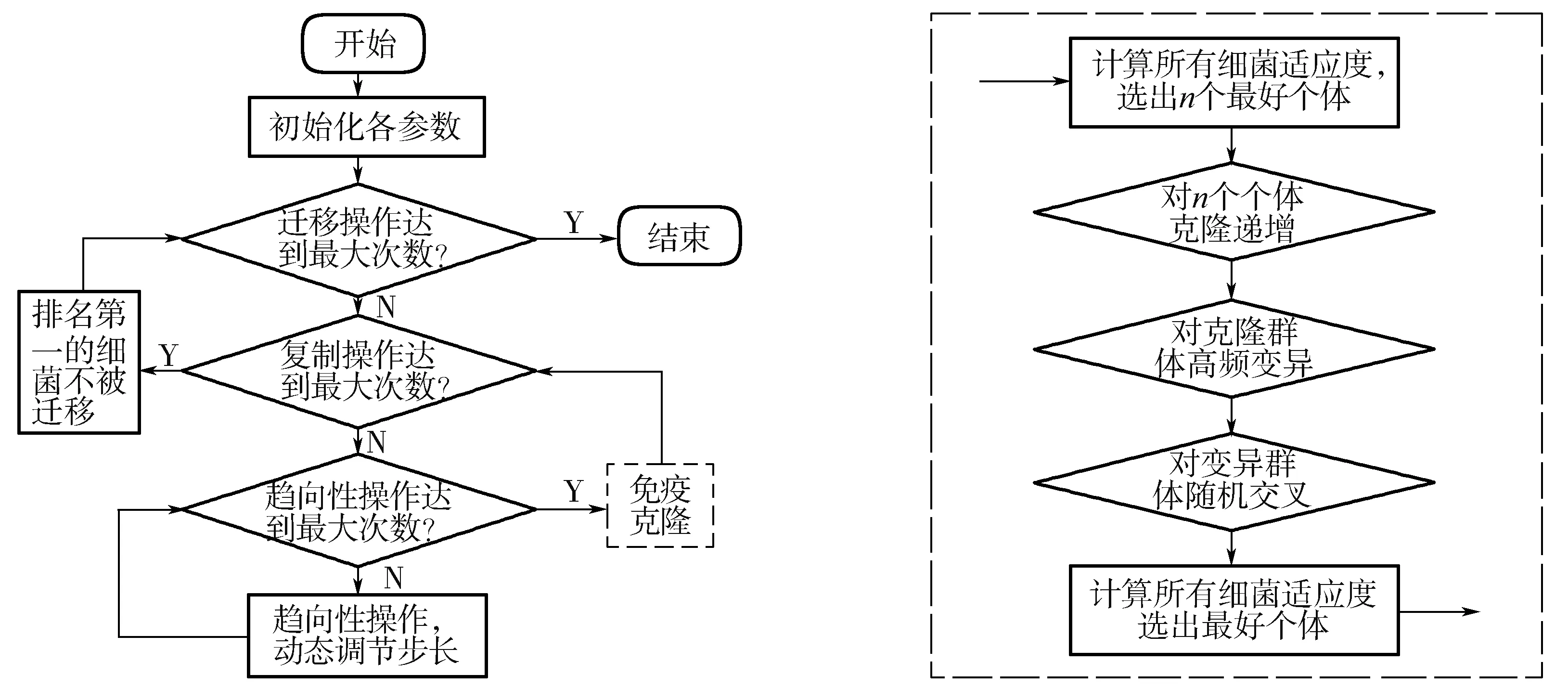
图1 GBFA算法流程

2.2 GBFA算法的敛散性

文献[11]、文献[12]对BFA算法的敛散性进行了研究[11-12]，但是文献[11]、文献[12]没有考虑BFA算法模拟菌群内部各个细菌个体之间的影响。笔者提出的GBFA虽然没有触及到传统BFA算法的定义基础，但是由于免疫算法的并入，需要重新证明GBFA的敛散性。

根据李涛的研究[13]：对于抗体种群A0，抗体空间几何为I*，v(A(k))为计算所得最优解的个数，B*为最优解的个数，

(18)

化简得到

P{v(A(k))≠0}+P{v(A(k+1))=

(23)

则有

k=1,2,….

(25)

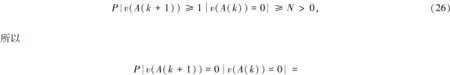
(32)

综上所述，GBFA以概率1收敛。

3 仿真实验

对旅客进行信息录入，列出所有可能路线，并利用GBFA进行计算，求解出最优目标函数。

3.1 简单显示条件下的计算

刘先生家在广东，来北京出差，居住在速八酒店景泰桥店(箭头所指方向)，如图2所示，希望看一下北京的一些古老建筑，比如明清的皇家园林等，但刘先生的时间比较短，时间预算为1 d，费用预算为500元。如果有可能的话，刘先生还想参观天安门广场的升旗仪式(非必须)。

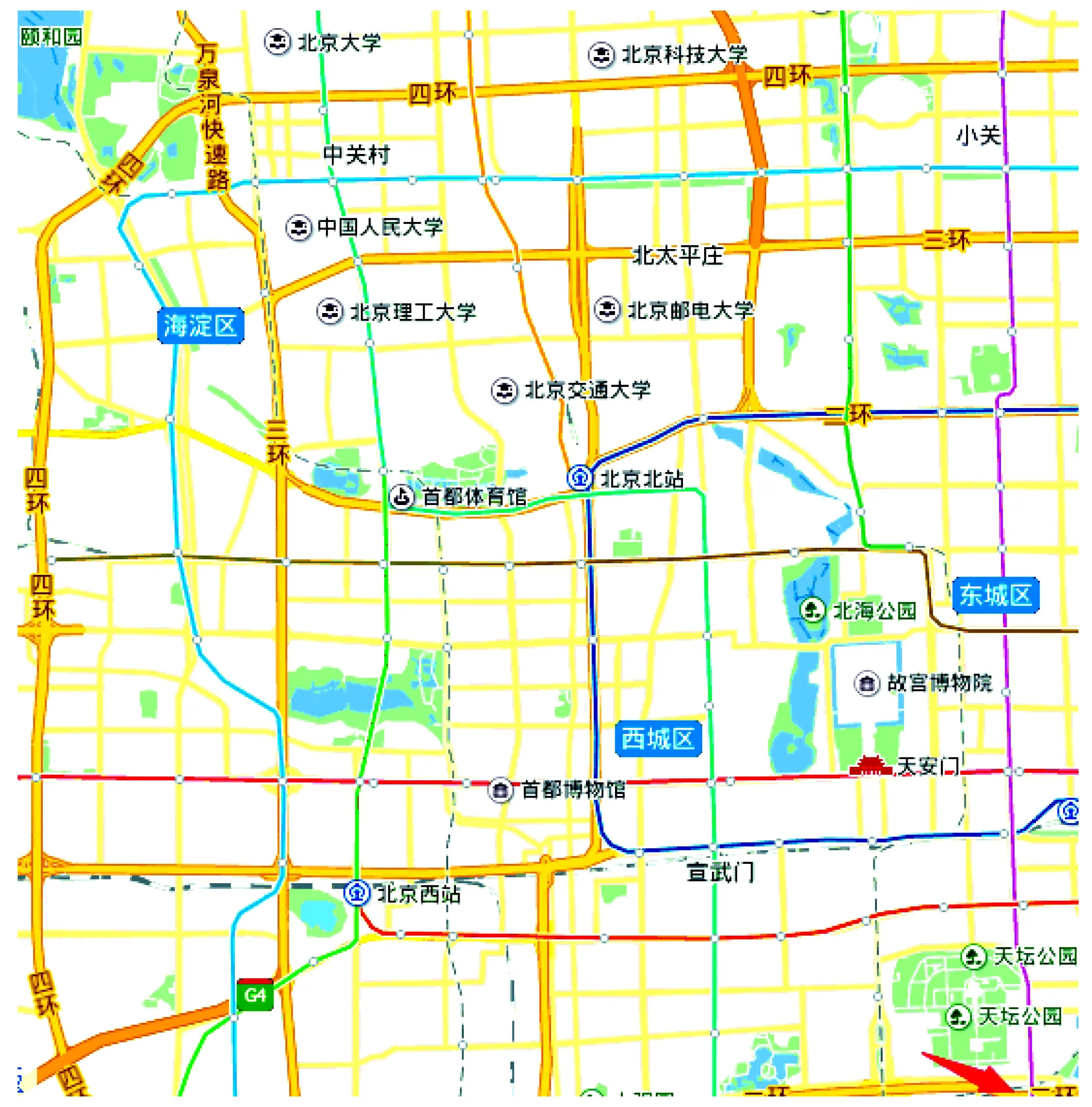
图2 景点位置

对于较近的距离，比如天安门到故宫，天坛到刘先生居住的地方，皆采用步行的方式，并不计费。其他用滴滴打车的方式，滴滴打车的方式约每公里1元。表1、表2给出了景点之间的距离、景点门票以及餐饮价格。

表1 景点之间的距离 km

表2 景点门票以及餐饮价格 元

针对上述实例，利用本文所提出的算法进行计算，结果如下：06:00天安门广场观看升旗仪式，之后观看毛主席纪念堂、人民大会堂外景、国家博物馆外景，并于天安门就餐；7:50以滴滴打车的方式去颐和园，游玩至12:00，并在颐和园就餐；13:00以滴滴打车的方式去故宫，游玩至17:00；17:00以滴滴打车的方式去天坛，游玩至21:00并于天坛就餐，结束行程，共花费329元。

针对计算结果进行分析，早晨刘先生先由居住地(速八酒店景泰桥店)到达天安门广场，因为天安门广场升旗时间较早，所以说首站定在天安门广场。在浏览天安门广场之后，此时故宫博物院尚未开门，而出城高峰期尚未至，故而可以避开上班高峰期，乘坐滴滴打车到达颐和园；在浏览颐和园之后，恰好避开出城高峰期，从颐和园回到故宫，参观故宫；由于天坛公园闭园较晚，所以最后游玩天坛公园，并于天坛公园就餐，之后刘先生由天坛公园步行回到旅馆休息。

3.2 复杂条件下的计算以及与其他方法的比较

假如有10名旅客同时去旅行，时间预算为30 d，费用预算为1万元，每名乘客有30个想要去的景点。这30个景点的位置为系统随机生成(可重复)，景点门票随机生成，景点附近的餐饮价格随机生成，但都位于欧洲和亚洲，不存在其他地区。程序计算结束条件有3个，满足任何一条皆退出计算。第一，费用预算达到1万元；第二，所有的景点皆被游览；第三，游览时间达到30 d。在程序计算之后，统计10名旅客游览的景点总数目以及花费的总数目。利用GBFA算法(E)对此进行计算，并与ILS-CS优化算法(A)、蚁群算法(B)、遗传算法(C)、蜂群算法(D)相比较，使用Pentium(R) Dual-Core CPU T4400，2.20 GHz，2 G内存，Win7X86操作系统，并考虑时差。

根据图3可以看出，5种方法在计算该题目的时候，蜂群算法(D)迭代次数最多，蚁群算法(B)次之，本文所使用的GBFA算法(E)迭代次数最少。GBFA算法(E) 迭代次数分别是前4种方法的9.83%、2.73%、34%、0.833%。

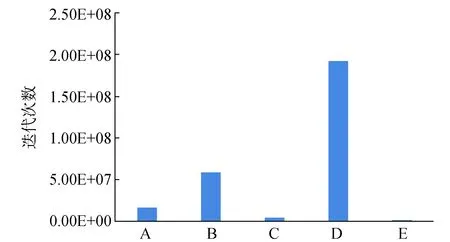
图3 5种算法的迭代次数

根据图4可以看出，5种方法在计算该题目的时候，蜂群算法(D)计算耗时最多，蚁群算法(B)次之，本文所使用的GBFA算法(E) 计算耗时最少。虽然ILS-CS优化算法(A)的迭代次数是遗传算法(C)迭代次数的3.5倍，但ILS-CS优化算法(A)的计算耗时是遗传算法(C) 计算耗时的1.08倍，这是因为ILS-CS优化算法(A)每一个迭代步的计算量较小。GBFA算法(E) 计算耗时分别是前4种方法的47%、44%、51%、18%。

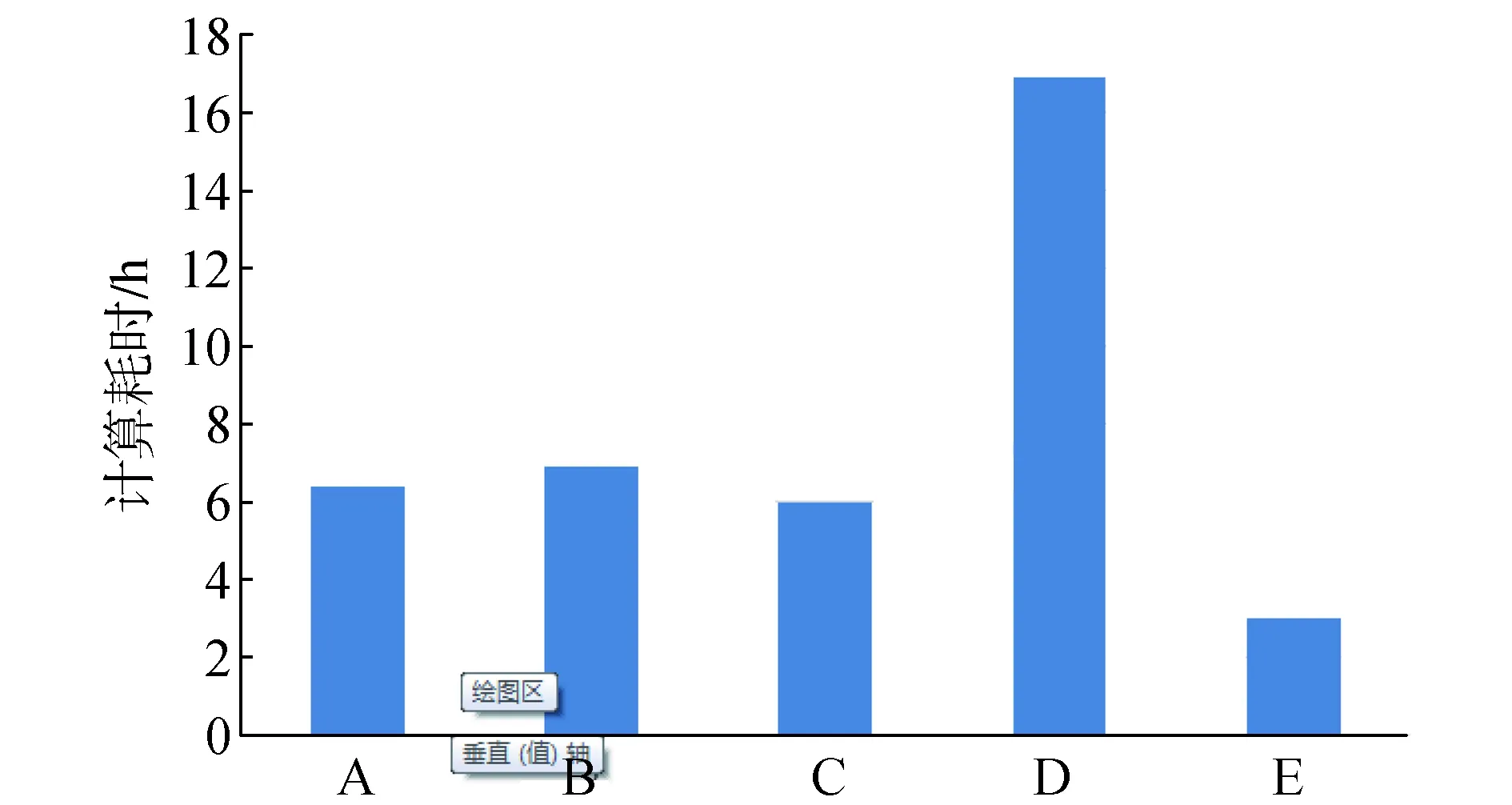
图4 5种算法的计算时间

表3列出的是5种计算方法的计算结果，分别就其休息时间、游玩时间、等待时间、交通时间、游览景点数目、花费进行统计，四项的和总共为720 h(30 d)。从表3可以看出，本文所提出的GBFA算法(E)，无论在休息时间、游玩时间、游览景点数目方面都是最高的，在等待时间、交通时间、花费方面都是最低的，说明本文所提出的GBFA算法(E)综合效果最佳，具有更好的适用性，其次为蜂群算法(D)。其休息时间分别是前四种算法的126%、112%、116%、108%，游玩时间分别是前四种算法的106%、105%、104%、102%，等待时间分别是前四种算法的32.5%、50%、37%、68%，交通时间分别是前四种算法的57%、65%、68%、77%，游览景点数目分别是前四种算法的113%、110%、113%、112%，交通时间分别是前四种算法的91%、88%、87%、89%。说明本文所提出的方法寻找的解比其他方法找到的解更加精确。

表3 5种算法的计算结果

4 结 论

在改进传统的细菌觅食算法提出免疫-细菌觅食算法，将免疫-细菌觅食应用到旅游路线选择问题模型中，并与常用的旅游路线选择问题模型算法相比较，结论显示：

1)免疫-细菌觅食算法充分考虑了景点的营业时间、餐饮费用以及交通时段，并由此来安排旅客的行程，使得旅客参观景点等待的时间最短，餐饮费用最低，交通所花费的时间最少；

2)与其他四种算法相比较，所使用的GBFA算法(E)迭代次数最少，分别是前4种方法的9.83%、2.73%、34%、0.833%；

3)与其他四种算法相比较，所使用的GBFA算法(E)计算耗时最短，分别是前4种方法的47%、44%、51%、18%；

4)与其他四种算法相比较，所使用的GBFA算法(E)寻找的解更加优化，在相同的限定条件下，本文所选取的方案可以游览更多的景点，游玩更长的时间，花费更少的钱财。

[1] TANG L, KAN Z, ZHANG X, et al. Travel time estimation at intersections based on low-frequency spatial-temporal GPS trajectory big data[J]. Cartography & Geographic Information Science, 2016.

[2] 尹阳. 基于节约里程算法的沥青配送线路优化研究——以厦门新立基沥青配送体系为例[J]. 长春工程学院学报(自然科学版), 2016(1).

[3] 肖海红, 蒋瑞波, 王兰洲,等. 基于GIS矢量数据结构的公交数据模型的实现[J]. 长春工程学院学报(自然科学版), 2015(3).

[4] SINGH, Harpreet, SKRYPCHUK, Lee. Route Planning Device and Associated Method:, WO/2016/026865[P]. 2016.

[5] 曹体涛,罗刊. 混沌微粒群优化算法及其在非线性函数参数估计中的应用[J]. 黑龙江工程学院学报,2014(5):54-56.

[6] WU Guang, JIANG Hui-xian, CHEN Fen. Research on Allocation of the Emergency Evacuation in and Around the Major Shopping Malls[J]. Journal of Fujian Normal University(Natural Science Edition), 2016.

[7] LIU Huiping, JIN Cheqing, ZHOU Aoying. Popular Route Planning with Travel Cost Estimation[M]// Database Systems for Advanced Applications. Springer International Publishing, 2016.

[8] TUAYCHAROEN N, SAKCHAROEN A, CHA-AIM W. Bangkok Bus Route Planning API[J]. Procedia Computer Science, 2016, 86:441-444.

[9] 黄恩洲. 基于粒子群—小波神经网络的短时交通量预测[J]. 黑龙江工程学院学报,2014(2):42-45.

[10] DENNERLINE R R. Database System To Organize Selectable Items For Users Related to Route Planning[J]. 2016.

[11] 侯乐, 杨辉华, 樊永显,等. 基于ILS-CS优化算法的个性化旅游线路研究[J]. 计算机科学与探索, 2016, 10(1):142-150.

[12] 王俊奇, 李闯, 董晔. Bishop 法的半解析解及其广义数学模型[J]. 水利与建筑工程学报, 2015(6):123-128.

[13] TANG W J, LI M S, HE S, et al. Optimal Power Flow With Dynamic Loads Using Bacterial Foraging Algorithm[C]// Power System Technology, 2006. PowerCon 2006. International Conference on. IEEE, 2006:1-5.

[14] DAS S，BISWAS A，DASGUPTA S，et al． Bacterial Foraging Optimization Algorithm: the Oretical Foundations，Analysis，and Applications [C]∥Foundations of Computational Intelligence Volume 3． Berlin / Heidelberg: Springer，2009: 23-55.

[责任编辑：郝丽英]

Research on the tourism route selection based on generate bacterial foraging algorithm

JIA Yunliang

(Shanxi Institute of Taxation, Taiyuan 030024，China)

For the rapid development of the tourism industry in the current situation, this paper explores the issue of which is widely concerned—the problem of tourism route selection. Aiming at the problem of tourism route selection, it makes it abstracted and generalized, transforming the problem of tourism route selection into the optimization problem of mathematical equation under certain conditions. Combined with the concept of immune algorithm and bacterial foraging algorithm, and compromising the idea of semi-analytical solution, this paper constructs a new optimization algorithm—Generate Bacterial Foraging Algorithm (GBFA) to solve the problem of tourism route selection, from the aspects of travel cost, play time and so on. The result shows: GBFA is much higher than other methods in computational efficiency, the cost of solution route is lower, the play time is increased, traffic time and waiting time are shorter, and the disposable rest time of visitors is more abundant, of which reflects this algorithm is more accurate, and the calculation process is more optimized.

path choice; waiting time; GBFA; expected cost

10.19352/j.cnki.issn1671-4679.2016.06.007

2016-06-02

贾润亮(1973-),男，讲师，研究方向：人工智能；计算机应用.

O246

A

1671-4679(2016)06-0029-06