LS+AR组合模型在大坝变形预报中的应用
2016-12-27林爱军
林爱军
(1.莆田市城乡勘测设计研究院,福建 莆田 351100)
LS+AR组合模型在大坝变形预报中的应用
林爱军1
(1.莆田市城乡勘测设计研究院,福建 莆田 351100)

针对大坝变形监测数据的年周期性特点,建立了大坝变形监测序列的拟合外推模型,提出了利用最小二乘外推(LS)与自回归(AR)组合模型预报大坝变形监测数据的方法。通过实验比较说明,LS+AR组合与AR模型相比,在大坝变形监测的预报精度上有一定程度的改善。
年周期性;变形监测;预报;LS+AR组合模型
变形是指变形体在各种荷载作用下,其形状、大小及位置在时空域中的变化[1]。大坝变形的影响因子主要有上下游水位的变化、温度变化和不可逆变化[2]。大坝在可控范围内的变形是允许的,但超过了适当范围,势必会带来严重的灾害后果,因此大坝的变形监测就显得尤为重要。目前,世界范围内的大坝都有长期连续的变形监测数据,从中可以了解以前大坝的变形情况,分析大坝产生变形的原因,更重要的是可利用这些数据对大坝未来的变形趋势进行预报,以达到提前评估大坝安全的效果。
关于大坝变形监测的预报,国内外学者从不同的角度分析建立了许多不同的预报模型。这些模型大体分为两类:一类是把大坝变形的形变量作为因变量,大坝变形的影响因子作为自变量,建立二者之间的统计表达式或具有物理意义的函数表达式,进而对大坝变形趋势进行模拟预报,主要有回归分析方法[2]、有限元方法以及二者的混合模型方法[3];另一类是把大坝变形的长期形变量作为时间序列,根据相邻时间点大坝变形形变量之间的相关性进行预报,主要有时间序列分析方法(AR、MA、ARMA)[4]和卡尔曼滤波模型[5]。另外,由于大坝变形的形变量与影响因子之间关系具有非线性、不确定的特点,因此人们利用神经网络模型黑匣子的特性对大坝变形进行预报[6],最终证明也是一种行之有效的方法。
大坝变形存在着趋势性周期变化,这种变化通常称为时效变形。利用小波方法对大坝变形监测数据进行分析,提取出大坝变形的长趋势项分量发现:随着环境量(库水位、气温)而变化的部分具有年周期变化的特点[7]。因此,本文针对大坝变形监测数据的年周期性特点,建立了大坝变形监测序列的拟合外推模型。首先利用LS对大坝变形监测序列进行拟合和外推,获得大坝变形监测序列的残差序列和外推值;然后利用AR模型对残差序列进行预测,最小二乘外推值与残差序列预报值之和为大坝变形数据的预报值。本文称这种模型方法为LS+AR组合模型。
1 组合预报模型
针对大坝变形监测序列的预报,首先对原始的监测序列进行预处理,然后分别采用AR模型方法和LS+AR组合模型方法进行预报。本文将详细介绍数据的预处理、AR模型和LS+AR组合模型的建模过程。
1.1 数据预处理
选用湖南省五强溪水电站大坝的水平位移监测数据,该数据是采用引张线法获得的绝对位移值,采样间隔为1 d。虽然引张线法能够实时连续地获取数据,但由于各种客观因素,观测数据总会存在一些问题,如观测数据中存在奇异值或观测数据中某一段时间没有数据。针对这些问题,本文采用“3σ准则”(σ指观测数据的中误差)和线性内插法[8]进行数据处理。
1.2 AR模型
目前,已经证明了利用AR模型对大坝变形监测数据进行预报的可行性[4]。其原理是把大坝变形监测数据作为一个时间序列,利用AR模型对其建模,然后进行预报。AR模型是一个概论统计模型。
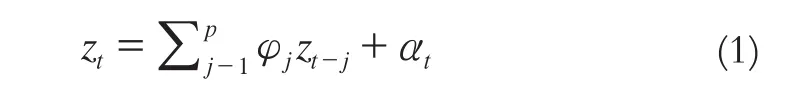
式中, zt(t=1,2,…,n)为平稳时间序列,此处为大坝变形监测序列;αt为白噪声:φ1、φ2、…、φp为模型参数;p为模型阶数。式(1)称为p阶AR模型,简称AR(p)[8]。
在使用AR模型进行大坝变形监测序列预报时, 模型阶数p采用最终预测误差准则来确定,其数学表达式为:
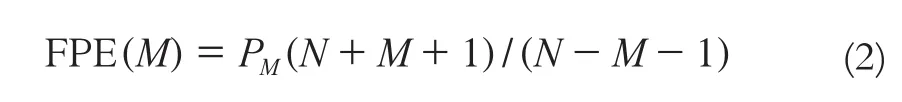
其中,

式中,PM为用AR模型去拟合zt的剩余均方误差,当M=1,2,…,N时,AR模型的阶数p为使得FPE(M)取最小值时的M值。AR模型的参数采用Le-Vinson递推算法求得[9]。
1.3 LS+AR组合模型
LS+AR组合模型是利用LS模型对大坝变形数据的年周期趋势项进行拟合外推,然后利用AR模型对残差序列进行预报,二者之和为大坝变形数据的最终预报值。在采用LS模型对年周期趋势项进行拟合外推前,首先要建立大坝变形监测序列的拟合外推模型,本文建立的数学表达式为:

式中,L(t)为大坝变形监测序列,t为时间;B1和B2为大坝变形监测序列的年周期项参数;P的取值为1,在进行拟合外推时单位换算为a。
关于AR模型对残差序列(大坝变形监测序列减去拟合序列的差值)的预报方法,在本文§1.2节中已经有介绍,不同之处是时间序列zt(t=1,2,…,n)为残差序列。
1.4 精度评定
为了证明LS+AR组合模型相对于AR模型在大坝变形监测序列预报上的优越性,本文对两种方法预报结果的精度作了比较。本文采用的精度评定指标[8]为平均绝对误差(MAE),其计算公式为:

式中,MAEi为预报跨度为i的平均绝对误差;pj为j 点的预测值;oj为j点的实际值;i为预报跨度;N为预报期的长度。
2 实验分析
本文选用2007-01-01~2008-08-21的大坝变形监测数据(水平位移监测值)进行实验,其中,选取2008-04-01~2008-08-21约5个月的数据作为预报期。采用AR模型和LS+AR组合模型两种方法对大坝变形监测序列进行了跨度分别为1、2、3、…、10 d的预报。两种方法的预报值与大坝变形监测值之间的差值见表 1。表1中的第4列为LS+AR组合模型相对于AR模型预报精度的改善情况。
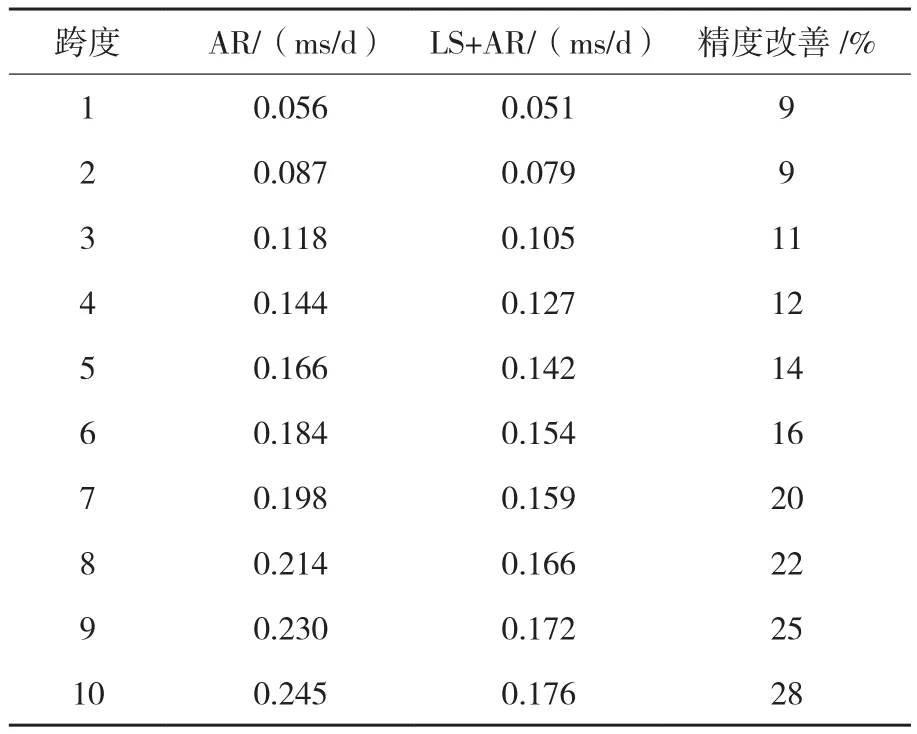
表1 两种模型日长变化预报结果的比较
从表1可以看出,LS+AR组合模型的预报精度相对于AR模型在1~10 d的跨度上都有一定程度的改善。其中,跨度为1~6 d的预报,精度改善为10%~15%;从跨度为7 d开始,LS+AR组合模型的改善精度越来越明显,最大改善是跨度为10 d的28%,可以预见随着跨度的逐渐增大,改善结果会更明显。
为了更加直观地展现LS+AR组合模型的可行性,本文给出了两种模型的平均绝对误差值图,如图1所示。
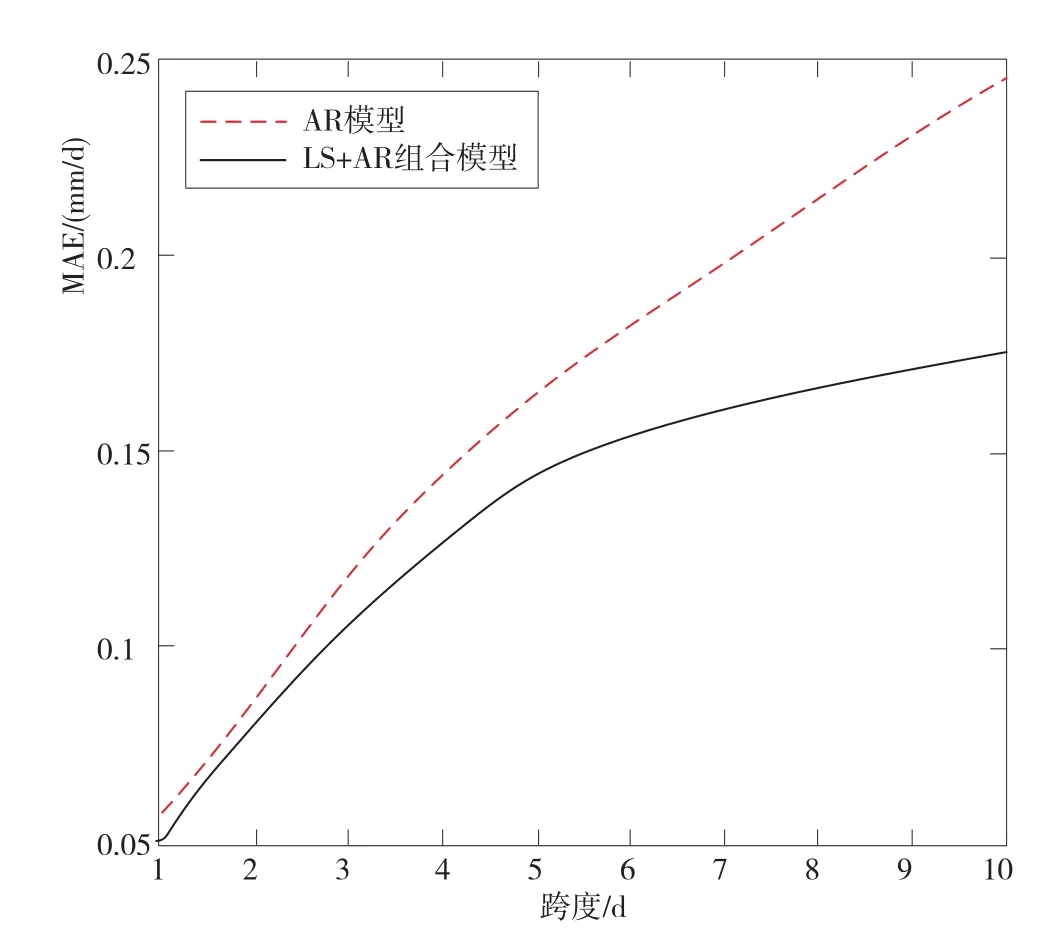
图1 两种模型所作的不同跨度大坝变形监测数据的精度比较
3 结 语
通过实验比较证明,本文采用的LS+AR组合模型方法比AR模型方法在大坝变形监测数据的预报精度上(跨度为1~10 d)有一定程度的改善,证明了该方法的可行性。同时,需要指出的是,本文对两种预报方法的比较是基于某一特定时间段,并没有考虑不同时间段数据对预报精度的影响;而且本文建立的拟合外推模型只考虑大坝变形监测的年周期性,并没有验证是否是最好的拟合模型;对于以上两点,笔者将会进行进一步研究。另外,大坝变形与库水位、温度等有密切关系,下一步将会考虑采用MAR模型对大坝变形监测序列进行预报,改善其预报精度。
[1] 黄声亨,尹晕晖,蒋征.变形监测数据处理[M].武汉:武汉大学出版社,2010
[2] 吴子安.大坝变形监测数据回归分析中的因子选择[J].武汉测绘科技大学学报,1993,18(1):20-26
[3] 吴中如.混凝土坝安全监控的确定性模型及混合模型[J].水利学报,1989(5):64-70
[4] 徐培亮.应用时间序列方法作大坝变形预报[J].武汉测绘科技大学学报,1988,13(3):23-31
[5] 王利,李亚红,刘万林.卡尔曼滤波在大坝动态变形监测数据处理中的应用[J].西安科技大学学报,2006,26(3):353-357
[6] 赵斌,吴中如,张爱玲.BP模型在大坝安全监测预报中的应用[J].大坝观测与土工测试,1999,23(6):1-4
[7] 徐洪钟,吴中如,李雪红,等.基于小波分析的大坝变形观测数据的趋势分量提取[J].武汉大学学报(工学版), 2003,36(6):5-8
[8] 刘大杰,陶本藻,朱建军,等.实用测量数据处理方法[M].北京:测绘出版社,2000
[9] 丁月蓉.天文数据处理方法[M].南京:南京大学出版社,1998
P258
B
1672-4623(2016)07-0110-02
10.3969/j.issn.1672-4623.2016.07.035
林爱军,工程师,主要从事GPS变形监测及现代测量数据处理工作。
2015-06-03。
项目来源:国家自然科学基金资助项目(U1231105、41404013)。
