二维各向异性海森堡反铁磁体的基态性质
2016-12-27区婉颜蒲秋容
区婉颜, 陈 渊, 蒲秋容
(广州大学 物理与电子工程学院, 广东 广州 510006)
二维各向异性海森堡反铁磁体的基态性质
区婉颜, 陈 渊*, 蒲秋容
(广州大学 物理与电子工程学院, 广东 广州 510006)
文章研究单离子各向异性影响下的二维正方晶格、自旋为1的阻挫海森堡反铁磁体的基态性质.利用自旋波方法,得到了在零温时该系统的奈尔相和共线相的子晶格磁化强度和基态能,发现了奈尔相-共线相转变的量子临界点依赖于单离子各向异性D以及次近邻反铁磁性耦合J2与最近邻反铁磁耦合J1的比值.在经典临界点J2/J1=0.5附近,当0≤D/J1≤0.03时系统存在一个中间无序顺磁相.自旋波的结果表明,在高于J2/J1=0.5区域,奈尔相-共线相转变是一级相变,发生在依赖于各向异性的临界线上.
海森堡反铁磁体; 基态性质; 自旋波方法; 单离子各向异性; 阻挫
0 Introduction
In recent years much attention has been paid to frustrated quantum Heisenberg antiferromagnets[1]. The discovery of the layered oxide high-temperature superconductors[2-3], shows that these systems can be well described by the two-dimensional frustrated spin-1/2 Heisenberg antiferromagnet. This model has been studied by various numerical techniques such as Quantum Monte Carlo (QMC), density matrix renormalization group, series expansion and exact diagonalization method[4-9]. This model has also attracted the interest of several analytical works that investigated the low-temperature properties and the ground-state phase diagram, such as field theory[10], spin-wave theory[11], path integral quantization[12], Green’s function method[13], effective-field theory technique[14], Schwinger boson mean-field theory[15], as well as renormalization group approach[16].
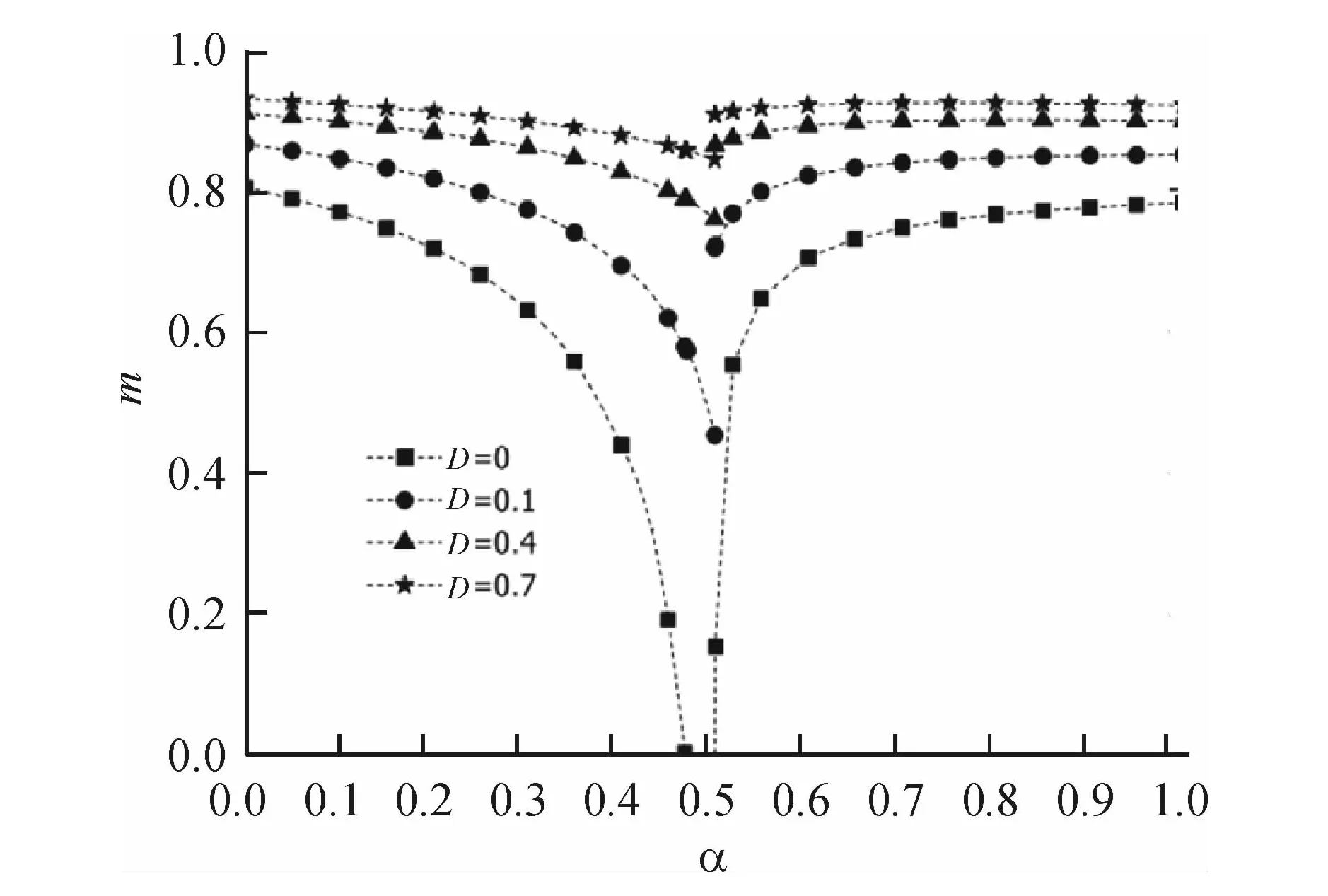
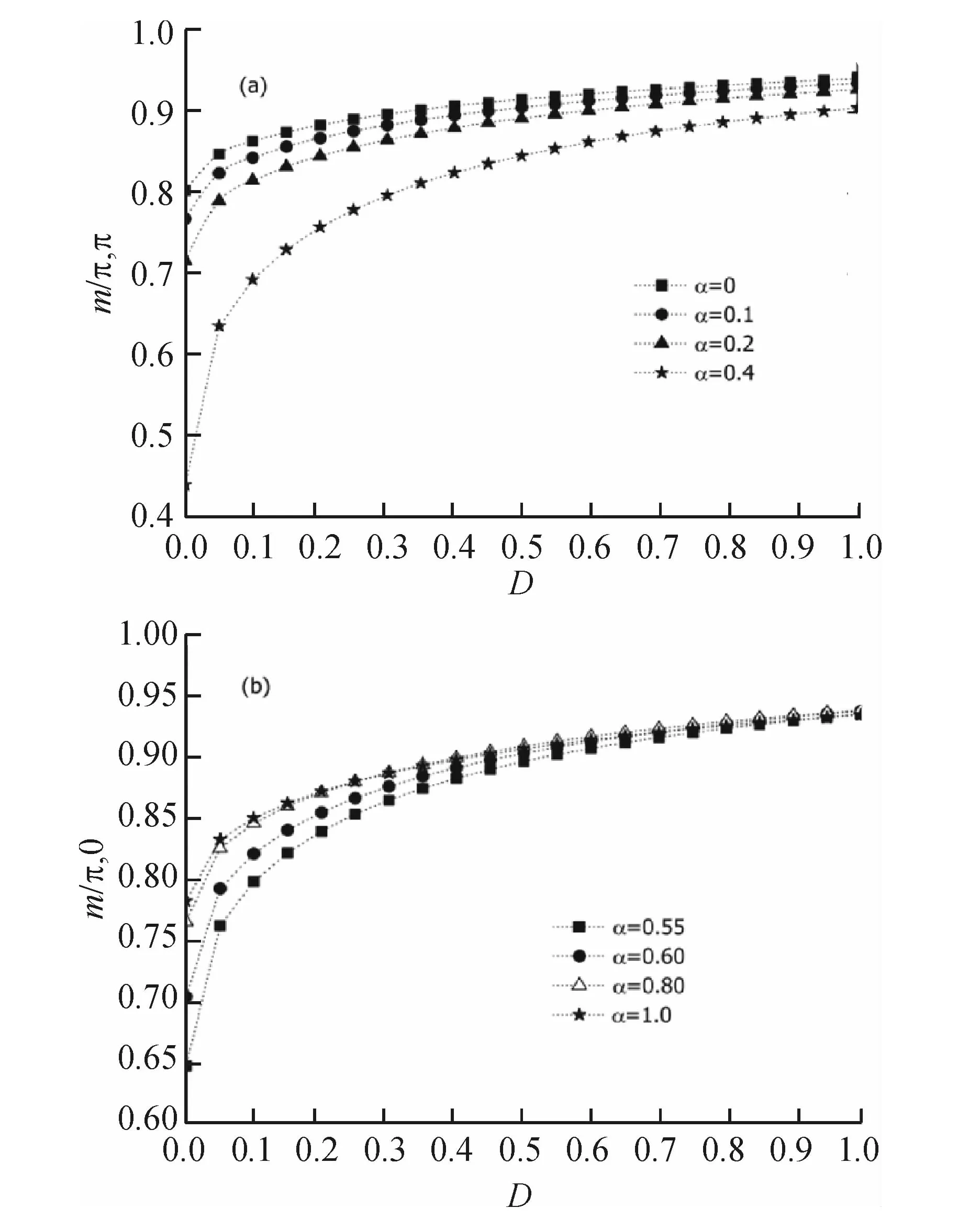
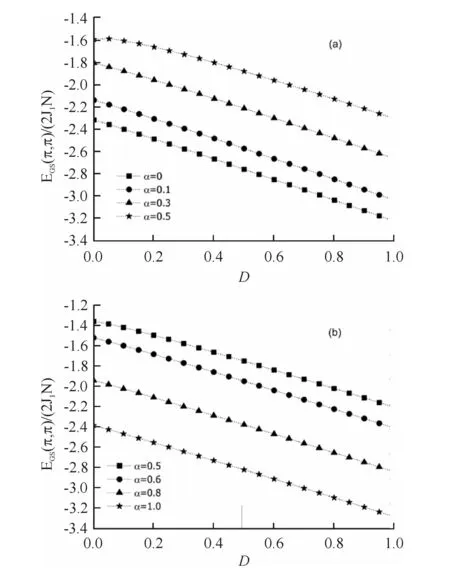
It seems to be clear now that the frustrated Heisenberg model[1], which includes nearest-neighbor (NN) antiferromagnetic couplingJ1and next-nearest-neighbor (NNN) antiferromagnetic couplingJ2, exhibits the Neel and collinear phases at smallJ2and at largeJ2, respectively. The Neel state is of two sublattices where all A-sublattice spins point in the direction of an arbitrary unit vector, while B-sublattice spins point in the opposite direction[11]. The collinear phase consists of two degenerate interpenetrating Neel states, each living on the initial sublattices A and B. The two ordered phases are separated by an intermediate quantum paramagnetic phase without magnetic long-range order in the parameter regionα1 However, many studies mentioned above mainly focused on the spin-1/2 frustrated case, and less investigation is for the spinS=1. It is known that the two-dimensional frustrated Heisenberg antiferromagnet might be used to describe the Fe monolayers in the Fe-based superconductors La-O-Fe-As[24-25]. It was suggested in Ref.[26] that the spin for the real La-O-Fe-As materials isn’tS=1/2, but isS≥ 1. Therefore, it is necessary to consider the case ofS=1. On the other hand, motivated by the spin anisotropies to the pure two-dimensional frustrated model, the effect of the single-ion anisotropy should be considered to better describe the real systems[18-21]. In this paper, our aim is to find out how the single-ion anisotropy affects the ground-state properties of the two-dimensional spin-1 frustrated system. We first discuss the frustrated Heisenberg model in the classical case of the spinS→ ∞. It is found that forJ2/J1< 1/2 the classical ground state is Neel ordered. While forJ2/J1> 1/2 the ordering is defined by the collinear phase. Then starting from these two classical ground states, we will apply the spin-wave method to studies on the two-dimensional spin-1 Heisenberg antiferromagnet with the single-ion anisotropy. Our spin-wave results show that a disordered region can survive for small anisotropy. If the single-ion anisotropy is strong enough, this disordered region disappears. In addition, it is found that aboveJ2/J1=1/2, there exists a first order phase transition from the Neel phase to the collinear phase at the transition point, which is dependent on the single-ion anisotropy. A brief outline of this paper is as follows. In section 1, by using the spin- wave theory, we present the basic equations for the ground-state properties. Section 2 contains the discussions and results. In section 3, a brief conclusion is given. We consider the two-dimensional frustrated Heisenberg model on the square lattice. The Hamiltonian of the model is defined as (1) The model (1) can be treated as the classical Heisenberg model in the limit of infinite spin,S→ ∞. The ground-state energy of the classical system is found to be Ecl(K)= 2NS2[J1(coskx+cosky+ 2αcoskxcosky)-D] (2) wherek=(kx,ky) is the wave vector. After the ground-state energy is minimized, the system displays two classical ground states. One is the classical two-sublattice Neel state whose ground-state energy Ecl(π,π)=-2NS2[2J1(1-α)+D] (3) occurs at the wavevectors (π,π) forα< 0.5. The other is the collinear state with the minimum energy Ecl(k)=-2NS2(2J1α+D) (4) atk=(π, 0) or (0, π) forα> 0.5. In the classical limit, the phase transition from Neel phase to collinear phase appears at the critical valueα=αc=1/2, which is the same to the two-dimensional isotropic cases[11,27-29]. In this section we will consider these two classical ground states as approximation to begin with, and investigate the effect of quantum fluctuations in the classical ground states. As mentioned above, when the original state is the Neel antiferromagnetic (NAF) phase [i.e. (π,π) phase] forα< 0.5, all the spins on the NN and NNN sites belong to the same and different sublattices respectively. In the regionα> 0.5, the ground state is collinear antiferromagnetic (CAF) state, where spins in order at wave vector (π,0) or (0, π). For the (π, 0) phase, all the NN spins along theyandxaxis belong to the same and different sublattices, respectively. And all the NNN spins still belong to different sublattice[11]. Starting from these two classical ground states, we employ the spin-wave theory to study the ground-state properties of the frustrated model. The fluctuations around the classical ground state are described by replacing the spins with boson creation and annihilation operators within the Holstein- Primakoff transformation[30] (5) for the spins in sublattice A and (6) for the spins in sublattice B. Here the Bose operatorsa+,b+anda,bare the creation and annihilation operators of spin deviations respectively. Using these transformations, we rewrite the Hamiltonian (1) in terms of bosonic operators, and keep only the leading terms up to the order of 1/S. Then the real space Hamiltonian (1) is transformed to the reciprocal space Hamiltonian, (7) with the help of the Fourier transforms In Eq.(7), the first termEclstands for the classical energiesEcl(π,π) andEcl(π, 0) for the Neel and collinear phases respectively. They have been given by Eqs.(3) and (4). The second and third terms account for the quantum fluctuations in the classical ground states. The coefficientsAkandBkare defined as Ak(π,π)=4J1S(1-α+αcoskxcosky)+D(2S-1) Bk(π,π)=2J1S(coskx+cosky) (8) in the NAF state, and Ak(π,0)=2J1S(2α+cosky)+D(2S-1) Bk(π,0)=2J1Scoskx(2αcosky+1) (9) in the CAF (π, 0) state respectively. The Hamiltonian can be diagonalized by the Bogoliubov transformation (10) (11) (12) (13) The commutation relations are preserved as (14) (15) Then the Hamiltonian is rewritten as (16) Here, the ground-state energyEGSand spin-wave energy ωkare obtained EGS(π,π)=-4J1NS2(1-α)-2NDS2+ (17) (18) in the NAF state, and EGS(π,0)= -4J1αNS2-2NDS2+ (19) (20) in the CAF (π, 0) state, respectively. In this section, we will use Eqs.(17)~(20) to investigate the ground-state properties of two-dimensional frustrated model for the spinS=1. In Subsection 2.1 and Subsection 2.2, we will discuss how the behaviors of the staggered magnetization and ground-state energy affected by the frustration and anisotropy, respectively. 2.1 Staggered magnetization Let us firstly consider the staggered magnetizationmwhich is defined by Using the Bogoliubov transformation,mis given by (21) (22) in the (π,π) and (π,0) phases, respectively. Here,ωk(π,π) andAk(π,π) [orωk(π,0) andAk(π,0)] can be obtained from the set of Eqs.(8) and (18) [or (9) and (20)]. Fig.1 Sublattice magnetization is plotted as a function of the frustration parameterα Fig.1 displays the frustration dependence of the staggered magnetization when the anisotropic parameterDis given. Here the interationJ1=1. It is found that in the Neel phase, the staggered magnetizationm(π,π) decreases monotonic- ally with increase in the frustrationα, but the staggered magnetizationm(π,0) increases in the collinear phase. It can be explained by the fact that forα< 0.5 the frustration gives rise to the quantum fluctuations strong, and spoils the Neel magnetic ordering. But forα> 0.5 the frustration weaken the quantum fluctuations, and maintains the collinear magnetic ordering. In Fig.2, we obtain the staggered magnetizationmas a function of the single-ion anisotropyD. When the frustration parameterαis given, both the magnetizationsm(π, π) andm(π, 0) have the similar increasing behavior from their minimum values atD=0 to the maximum values atD=1. This is because the single-ion anisotropyDhas a tendency to decrease the quantum fluctuations in the ground states, and helps to stabilize the magnetic orderings in the Neel and collinear phases. Fig.2 The staggered magnetizations, (a)m(π,π) in the Neel phase, and (b)m(π,0) in the collinear phase, are plotted as a function of the frustration parameterD When the anisotropic parameterDis given. Here the interactionJ1=1. Note that this kind of frustration-dependent behavior at very smallDis slightly different from that at largeD. ForD=0,m(π,π) decreases from 0.803 4 at α=0 to zero at α=0.4682 3, andm(π,0) decrease from 0.78167 at α=1 to zero at α=0.500 35. IfDis very small, bothm(π,π) andm(π, 0) still have this kind of behavior. However, for largeD, bothm(π,π) andm(π, 0) can not change to zero as α approaches 0.5 from both sides. Table 1 The values of the staggered magnetizationm(π, π) for different anisotropic parametersDin the Unfrustated case D00.10.20.51Ours0.803400.864560.884510.916240.94184series0.804830.839110.859450.933760.96141 The series values[31]are obtained by series expansions. In the Unfrustated caseα=0, the values of the staggered magnetizationm(π,π) are listed in Table 1 for different anisotropic parametersD. The series values[31]are obtained by series expansions. As pointed out in Ref.[32] series expansions methods allow rather precise calculation of ground-state properties of the magnetic systems. Although the simple Linearlized spin wave is used in this paper, our spin-wave results ofm(π,π) are in almost quantitative agreement with the series results. Table 2 The values of the staggered magnetization m for different frustration parameters α in the case of D=0.01 Table 3 The values of the staggered magnetization m(π, 0) for different frustration parameters D in the isotropic case In the caseD=0.01, the values of the staggered magnetizationm(π, 0) are listed in Table 2 for different frustration parameters α. The GFM values[33]are obtained by the many-body Greens Function Method (GFM) under random phase approximation. Our spin-wave results ofmare in almost quantitative agreement with the GFM values, except for the region of α=0.5 nearby. Spin-wave theory in the NAF phase becomes unstable close to the classical transition point α=0.5 for 0≤D≤0.03. At α=0.5, the value of the staggered magnetizationm(π, π) is zero, which means the existence of a new disordered state. In the isotropic limit ofD=0, the values of the staggered magnetizationm(π, 0) are shown in Table 3 for different frustration parameters α. It is found that our spin-wave results ofm(π, 0) roughly agree with the series data and the SCSWT values, which are obtained[34]by series expansion method and self-consistent spin wave theory (SCSWT) respectively. Compared with the highly precise data[34], our results are better than the results obtained[35]by the bond operator technique (BOT). The dash and heavy solid lines indicate the critical points, α1and α2, for the NAF and CAF phases, respectively. The dash-dot denotes the phase transition between the CAF and Disordered phases at α=0.5. The solid line is for the phase transition between the NAF and CAF phases at α=0.5. Here α is the frustration parameter, and D is for the single-ion anisotropy. The interaction is set asJ1=1. Fig.3 displays the phase diagram for the frustrated model on a square lattice. The system contains three phases: NAF, CAF, and disordered paramagnetic phases. In Fig.3, the solid line is for the phase transition between the NAF and CAF phases at the classical transition pointαcl=0.5. The dash-dot denotes that the phase transition from the CAF to disordered phases happens atα=0.5. The dash and heavy solid lines indicate the critical points,α=α1andα=α2, of the NAF and CAF phases for 0 ≤D≤ 0.03 and 0 ≤D≤ 0.002 respectively. Hereα1(orα2) is given bym(π,π)=0 [orm(π,0)=0].α1(α2) stands for the critical point of the phase transition from the Neel (collinear) phase to a disordered paramagnetic state. Fig.3 and Table 4 both show thatα1grows up as the single-ion anisotropyD, butα2decreases. ForD=0, ourα2is in agreement with the SCSWT value[34]. However, the BOT valuesα2deviates largely from ours. Fig.3 The phase diagram for the frustrated model D00.00050.0010.002BOTSCSWTα10.46823000.47370000.47590000.47900000.4200000α20.50035560.50004810.50000120.50000010.56400000.50413 It is noticed that the critical line (α=α1) of the NAF is longer than the critical line (α=α2) of the CAF in Fig.3. This is because the frustrations play different poles in the Neel and collinear phases. It tends to weaken the Neel magnetic ordering, but helps the collinear magnetic ordering. In addition, the single-ion anisotropyDgives a hand to the magnetic ordering. This leads to that the staggered magnetizationm(π, 0) more difficultly approaches zero thanm(π,π) which can vanish along the critical lineα=α1only for 0 ≤D≤ 0.03.m(π,0)=0 becomes zero atα=α2for 0 ≤D≤ 0.002. But aboveD=0.002,m(π,0) is nonzero atα=0.5. It is shown in Fig.3 that there exists an intermediate region of the disordered paramagnetic state when 0 ≤D≤ 0.03 and 0.468 23 ≤α≤0.500 36. This result disagrees with existence of the disordered region as predicted[33]by GREEN’s function method. For 0.03 2.2 Ground state energy In this section, we will use Eqs.(17) and (19) to discuss the behaviors of the ground-state energy affected by the frustration and anisotropy. In Fig.4 we show the ground-state energy per site,EGS/(2NJ1), for the NAF and CAF phases as a function of the anisotropic parameterD. When the frustration parameterαis given, the ground-state energyEGSdecreases with increasingDin the whole anisotropy region no matter what the NAF and CAF states. Note that the ground-state energy measures the quantum fluctuations. The larger the anisotropy Fig.4 Ground state energies per site, (a)EGS(π, π)/(2NJ1) and (b)EGS(π, 0)/(2NJ1) are plotted as a function of the anisotropic parameterD D, the weaker the quantum fluctuations, the more the ground-state energyEGSshortens. Fig.5 shows the ground-state energy per site,EGS/(2NJ1), as a function of the frustration parameterα. When the single-ion anisotropyDis given, it is observed that the ground-state energy has two kinds of different frustration-dependence behaviors, which is similar to the isotropic cases[4, 11, 13]. Asαincreases from zero to 0.5, the ground-state energyEGS(π,π) increases in the NAF phase. While for 0.5 ≤α≤ 1,EGS(π, 0) decreases with increasingαin the CAF phase. Since the different poles in quantum spin fluctuations are played by the frustration and anisotropy in both phases,EGS(π,π) of the NAF phase is all smaller thanEGS(π, 0) of the CAF phase atα=0.5 ifDis fixed. This is very different from the equal energies atα=0.5 in the two-dimensional classical cases. Fig.5 Ground state energy per site,EGS/(2NJ1), is plotted as a function of the frustration parameterα Table 5 The values of the ground-state energy per site for different anisotropic parameters D in the Unfrustated case In the Unfrustated case, the values of the ground-state energy per siteEGS/(2NJ1) are listed in Table 5 when the single-ion anisotropy is set to beD=0,0.1,0.2,0.5, 1, respectively. It is shown in Table 5 that ourEGS/(2NJ1) are close to the series values[31]forα=0. As mentioned above, the classical ground-state energy of the NAF phase meets that of the CAF phase at the classical transition point α=0.5, which signals that a first-order phase transition from the NAF phase to the CAF phase occurs at α=0.5. It is interesting where a first-order quantum phase transition occurs from NAF to CAF phase. In the isotropic quantum two-dimensional cases[27-29], this kind of the first-order quantum phase transition is confined to the region of 0.5 <α<0.6. In three dimensions, due to quantum spin fluctuations the first-order phase transition point is shifted to α=0.72[22]. Fig.6 The first-order quantum phase transition point,αc, is plotted versus the anisotropic parameterD Like the isotropic cases, afterEGS(π,π) of the NAF phase is extrapolated above α=0.5 in the existence of the anisotropy, we find that the two energiesEGS(π,π) andEGS(π,0) meet at α=αc. This point indicates a first-order quantum phase transition from NAF to CAF phase. The anisotropy dependence of αcis displayed in Fig. 6. At small anisotropies 0≤D≤0.3, the first-order phase transition point αcis fitted to the linear law behavior αc=0.582 44-0.109 75D (23) But in the larger-anisotropy region 0.4≤D≤1, Fig.6 shows thatαcmay be described by the linear law αc=0.554-0.03D (24) In this work, we have studied the ground-state properties of the spin-1 frustrated Heisenberg antiferromagnet on the square lattice. Starting from two classical ground states, the effect of quantum fluctuations in the classical ground states is investigated within the spin wave method. The lattice magnetizations as well as ground-state energies of the system are obtained for the Neel and collinear phases. They are found to be dependent on both the anisotropy and frustration. It is shown that the single-ion anisotropy and frustration play different roles in quantum fluctuations. The single-ion anisotropyDhas a tendency to decrease the quantum fluctuations, and helps to stabilize the magnetic ordering. This leads to that in the Neel and collinear phases, the sublattice magnetizations all increase with the increasingD, but ground-state energies decrease. However, the frustrationJ2helps the quantum fluctuations in the NAF state, but spoils in the CAF state. Then it gives rise to that the NAF lattice magnetizationm(π,π) and CAF ground-state energyEGS(π,0) de- crease as the frustration parameterα=J2/J1increases, but the CAF latticemagnetiza -tionm(π, 0) and NAF ground-state energyEGS(π,π) increase. Our spin-wave results shows that there exists an intermediate region of the disordered paramagnetic state when 0 ≤D≤ 0.03 and 0.468 23 ≤α≤0.500 36. This result denies the existence of the disordered region as predicted[33]by GREEN’s function method. AsDrises fromD=0, the region of the disordered paramagnetic state become narrow. AtD=0.03, the disordered region disappears. For 0.03 Finally, we find that the two energiesEGS(π,π) andEGS(π,0) meet atα=αcafter the ground-state energyEGS(π,π) of the NAF phase is extrapolated aboveα=0.5. These pointsαcindicate a first-order quantum phase transition from NAF to CAF phase, which is different from a first-order classical phase transition from the NAF to the CAF phase occurring atα=0.5. The first-order quantum phase transition point,αc, is well fitted to the linear laws at both small and large anisotropies. But the laws are on the negative slope -0.109 75 for 0 ≤D≤ 0.3, and -0.03 for 0.4 ≤D≤ 1, respectively. [1] DIEP H T. Frustrated spin systems[M]. Singapore:World Scientific Publishing Co Pte Ltd, 2005. [2] BOMBARDI A, RODRIGUEZ-CARVAJAL J, MATTEO S D, et al. Direct determination of the magnetic ground state in the square lattice S=1/2 antiferromagnet Li2VOSiO4[J]. Phys Rev Lett, 2004, 93: 027202. [3] CHRISTENSEN N B, MCMORROW D F, RONNOW H M, et al. Deviations from linear spin wave theory in the 2D. S=1/2 Heisenberg antiferromagnet CFTD[J]. J Magn Magn Mater, 2004, 896: 272-276. [4] SANDVIK A W, SINGH R R P. High-energy magnon dispersion and multimagnon continuum in the two-dimensional heisenberg antiferromagnet[J]. Phys Rev Lett, 2001, 86: 528-531. [5] YUNOKI S, SORELLA S. Resonating valence bond wave function for the two-dimensional fractional spin liquid[J]. Phys Rev Lett, 2004, 92: 157003. [6] WHITE S R, CHERNYSHEV A L. Neél order in square and triangular lattice Heisenberg models[J]. Phys Rev Lett, 2007, 99: 127004. [7] ZHENG W H, OITMAA J, HAMER C J. Series studies of the spin-1/2 Heisenberg antiferromagnet at T=0:Magnon dispersion and structure factors[J]. Phys Rev B, 2005, 71: 184440. [8] RICHTER J, SCHULENBURG J. The spin-1/2 J1-J2 Heisenberg antiferromagnet on the square lattice: Exact diagonalization for N=40 spins[J]. Eur Phys B, 2010, 73: 117-124. [9] SCHMIDT B, SIAHATGAR M, THALMEIER P. Ordered moment in the anisotropic and frustrated square lattice Heisenberg model[J]. Phys Rev B, 2011, 83: 075123. [10]ISAEV L, ORTIZ G, DUKELSKY J. Hierarchical mean-field approach to theJ1-J2Heisenberg model on a square lattice[J]. Phys Rev B, 2009, 79: 024409. [11]WU Y, CHEN Y. Modified spin-wave theory for the frustrated Heisenberg antiferromagnet on a square lattice[J]. Int J Mod Phys B, 2013, 27: 1350021. [12]KRUGER F, SCHEIDL S. Frustrated Heisenberg antiferromagnets: Fluctuation-induced first order vs. deconfined quantum criticality[J]. Europhys Lett, 2006, 74: 575-578. [13]SCHMALFU D, DARRADI R, RICHTER J, et al. QuantumJ1-J2antiferromagnet on a stacked square lattice: Influence of the interlayer coupling on the ground-state magnetic ordering[J]. Phys Rev Lett, 2006, 97: 157201. [14]MENDONCA G, LAPA R, DESOUSA J R, et al. The ground state phase diagram of the quantumJ1-J2spin-1/2 Heisenberg antiferromagnet on an anisotropic square lattice[J]. J Stat Mech, 2010: P06022. [15]MERINO J, HOLT M, POWELL B J. Spin-liquid phase in a spatially anisotropic frustrated antiferromagnet: A schwinger boson mean-field approach[J]. Phys Rev B, 2014, 89: 245112. [16]ORTH P P, CHANDRA P, COLEMAN P, et al. Emergent criticality and Friedan scaling in a two-dimensional frustrated Heisenberg antiferromagnet[J]. Phys Rev B, 2014, 89: 94417. [17]COLDEA A I, SEABRA L, MCCOLLAM A, et al. Cascade of field-induced magnetic transitions in a frustrated antiferromagnetic metal[J]. Phys Rev B, 2014, 90: 020401(R). [18]ROSCILDE T, FEIGUIN A, CHERNYSHEV A L, et al. Anisotropy-induced ordering in the quantumJ1-J2antiferromagnet[J]. Phys Rev Lett, 2004, 93: 017203. [19]VIANA J R, DESOUSA J R. Anisotropy effects in frustrated Heisenberg antiferromagnets on a square lattice[J]. Phys Rev B, 2007, 75: 052403. [20]BISHOP R F, LI P H Y, DARRADI L R, et al. The quantumJ1-J1′-J2spin-1/2 Heisenberg model: Influence of the interchain coupling on the ground-state magnetic ordering in two dimensions[J]. J Phys: Condens, Matter, 2008, 20: 255251. [21]MAJUMDAR K. Second-order quantum corrections for the frustrated spatially anisotropic spin-1/2 Heisenberg antiferromagnet on a square lattice Kingshuk Majumdar[J]. Phys Rev B, 2010, 82: 144407. [22]MAJUMDAR K, DATTA T. Non-linear spin wave theory results for the frustrated S=1/2 Heisenberg antiferromagnet on a body-centered cubic lattice[J]. J Phys: Condens. Matter, 2009, 21: 406004. [23]GÖTZE O, RICHTER J. Ground-state phase diagram of the XXZ spin-s kagome antiferromagnet: A coupled-cluster study[J]. Phys Rev B, 2015, 91: 104402. [24]TAKAHASHI H, IGAWA K, ARII K, et al. Superconductivity at 43 K in an iron-based layered compound LaO1-xFxFeAs[J]. Nature (London), 2008, 453:376. [25]CHEN G F, LI Z, WU D, et al. Superconductivity at 41 K and its competition with spin-density-wave instability in layered CeO1-xFxFeAs[J]. Phys Rev Lett, 2008, 100: 247002. [26]MA F, LU Z Y, XIANG T. Arsenic-bridged antiferromagnetic superexchange interactions in LaFeAsO[J]. Phys Rev, 2008, B78: 224517. [27]CHANDRA P, COLEMAN P, LARKIN A L. A quantum fluids approach to frustrated Heisenberg models[J]. J Phys: Condens Matter, 1990, 2: 7933. [28]NISHIMORI H, SAIKA Y. Modified spin wave theory of the two-dimensional frustrated heisenberg model[J]. J Phys Soc, Jpn, 1990, 59: 4454. [29]MILA F, POILBLANC D, BRUDEF C. Spin dynamics in a frustrated magnet with short-range order[J]. Phys Rev B, 1991, 43: 7891. [30]HOLSTEIN H, PRIMAKOFF H. Field dependence of the intrinsic domain magnetization of a ferromagnet[J]. Phys Rev, 1940, 58: 1098-1113. [31]OITMAA J, HAMER C J. Ground-state properties and one-particle spectra for a spin-1 Heisenberg antiferromagnet from series expansions[J]. Phys Rev B, 2008, 77: 224435. [32]OITMAA J, HAMER C J, ZHENG W. Series expansion methods for strongly interacting lattice models[M]. Cambridge: Cambridge University Press, 2006. [33]WANG H Y. Phase transition of square-lattice antiferromagnets at finite temperature[J]. Phys Rev B, 2012, 86: 144411. [34]UHRIG G S, HOLT M, OITMAA J, et al. Pnictides as frustrated quantum antiferromagnets close to a quantum phase transition[J]. Phys Rev B, 2009, 79: 092416. [35]PIRES A S T. Frustration and quantum phase transitions in an anisotropic antiferromagnet on a square lattice[J]. Phys A, 2011, 390: 2787. 【责任编辑: 陈 钢】 The ground-state properties of two-dimensional frustrated Heisenberg antiferromagnet OUWan-yan,CHENYuan*,PUQiu-rong (School of Physics and Electronic Engineering, Guangzhou University, Guangzhou 510006, China) The effect of the single-ion anisotropy on the ground-state properties of the spin-1 frustrated Heisenberg antiferromagnet is investigated on a square lattice. The sublattice magnetizations as well as ground-state energies of the system are obtained within the spin-wave method for the Neel and collinear phases at zero temperature. It is found that the quantum critical points for the Neel and collinear phases are dependent on the single-ion anisotropyDand the ratio of next-nearest-neighbor antiferromagnetic couplingJ2to nearest-neighbor antiferromagnetic couplingJ1. Near the classical pointJ2/J1=0.5, there is an intermediate disordered paramagnetic phase for 0≤D/J1≤0.03. Our spin-wave results show that a first order phase transition from the Neel phase to the collinear phase occurs at the anisotropy-dependence critical line aboveJ2/J1=0.5. Heisenberg antiferromagnet; ground-state property; spin-wave method; single-ion anisotropy; frustration O 482.52 Document code: A Foundation items: Supported by the National Natural Science Fund of China (10974059) 1671- 4229(2016)05-0042-10 O 482.52 A Received date: 2016-05-11; Revised date: 2016-05-18 Biography: OU Wan-yan(1992-), female, postgraduate. E-mail: 1019713773@qq.com *Corresponding author. E-mail: chenyuan@gzhu.edu.cn
2 Model

2 Results and discussions
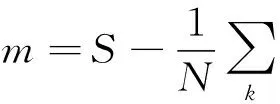








3 Summary
