基于SVD的EMD模态混叠消除方法

张小明，唐 建，韩 锦

(1.解放军理工大学 野战工程学院，南京 210007；2.西北工业集团有限公司 物流中心，西安 710043)

基于SVD的EMD模态混叠消除方法

张小明1，唐 建1，韩 锦2

(1.解放军理工大学 野战工程学院，南京 210007；2.西北工业集团有限公司 物流中心，西安 710043)

为了改进EMD中模态混叠的缺陷，提出一种基于SVD的模态混叠消除方法。SVD有两个特性，一是每个频率成分对应两个大小相当的奇异值；二是各频率成分经分解得到的奇异值大小与该频率成分的振幅呈正相关。该方法根据信号中主要频率成分构造出一组与原信号频率相等、幅值与原信号振幅成整倍数的正弦信号，并与原信号叠加后对叠加信号进行SVD分解，然后成对选取分解得到的奇异值重构出一组信号，依次减去前面加入的对应频率的正弦信号即可得到分解结果。实验表明，对于EMD分解模态混叠现象严重的信号，该方法能够进行有效消除模态混叠。

振动与波；EMD；模态混叠；SVD；构造信号

EMD(EmpiricalModeDecomposition)是 由Huang等提出的一种信号的时域分解方法，它能将信号由高频至低频分解成一系列 IMF(Intrinsic Mode Functions)分量，该方法尤其擅长分解非线性、非平稳信号[1-2]。在EMD分解中，理想的分解结果是信号中的每一个频率成分被单独地分到一个IMF分量中。但是在实际应用中，往往会出现单个IMF分量中含有多个频率成分，或者是一个频率成分会发散到多个IMF分量中，即发生模态混叠[3]。尤其是当信号中的各成分频率比较接近的时，模态混叠更易发生。

模态混叠产生的原因有两方面，一是在采用三次样条拟合情况下上下包络时产生过冲和欠冲。在插值方法的改进上，学者们提出了B样条插值法[4]、分段抛物线插值法[5]、分段幂函数插值法[6]、保持分段三次插值方法等[7]。这些方法在一定程度上抑制了过冲和欠冲，改善了模态混叠现象。二是方法本身的缺陷。在方法改进方面，Huang等提出了EEMD(Ensemble Empirical Mode Decomposition)[3]，采用向信号中加入多组白噪声、分别分解后再求平均的方法来抑制模态混叠，但该方法面临着如何选取合适的噪声组数和方差的困难；Ryan Deering等提出掩膜信号法[8]，通过对原信号分别加上和减去一个掩膜信号分别进行EMD分解，再对IMF分量做平均；赵玲等进一步对平均瞬时频率进行修正来改进掩膜信号[9]，掩膜信号法需要针对不同的信号确定不同的掩膜信号，而且用Hilbert变换估计出的瞬时频率偏差比较大，该方法在分离含有频率成分比较接近的信号时效果并不好。

奇异值分解(Singular Value Decomposition，SVD)是一种通过矩阵运算进行信号分解的方法，该方法被学者们用来进行信号的降噪和特征提取[10-13]。原信号先被转换成一个Hankel矩阵，再通过SVD得到两个酉矩阵和一个对角矩阵，通过选取对角矩阵中奇异值重构信号中的成分。SVD完全根据信号本身的特征进行自适应的分解，尤其擅长分解平稳信号。

SVD分解有两个特点，一是原信号中的每个频率成分对应大小相当的两个奇异值[14]；二是代表不同频率成分的奇异值的大小与该频率的幅值呈正相关。根据SVD分解的这两个特点，由信号中的主要频率成分先构造一组频率相等、振幅已知的正弦信号，再将这组信号与原信号叠加，用各正弦信号已知的振幅关系来掩盖原信号中各频率成分模糊的振幅关系，叠加信号经SVD处理后重构出一组信号，再分别减去对应频率的正弦信号，最终得到原信号中各频率成分的时间序列。

1 SVD简介

信号x可以根据Hankel矩阵形式被构造成一个信号矩阵，构造方法如下

式(1)中H是一个m×n的矩阵，N为信号x的长度；n为Hankel矩阵的列数(1＜n＜N)；m为矩阵的行数(m=N-n+1)。

对H进行SVD分解

式(2)中U是m×m的酉矩阵，S是m×n的对角矩阵，V是n×n的酉矩阵。其中，S可表示成

式(3)中∑=diag(σ1,σ2,…,σr)，σ1＞σ2＞…＞σr＞0。

这种变换本质上是将原始信号分解为一系列分量信号的简单线性叠加，而这一系列分量可以通过单独选取S中对角线上的奇异值重构获得，且重构出的信号的相位和它在原信号中叠加的相位是不变的，即具有零相位偏移特性。

2 基于SVD消除EMD中模态混叠

2.1 SVD的典型特点

通过其他学者的研究[14]及相关实验，得到SVD的以下两点性质。

(1)对于仅含有一个频率成分的信号，其Hankel矩阵经SVD分解后，能在对角矩阵S的前2阶获得两个较大的奇异值，其他阶的奇异值很小；而含两个频率成分的信号经SVD分解后，其前4阶奇异值较大，其他阶的奇异值很小。依此类推，含有k个频率成分的信号经SVD分解后，对角矩阵S的前2k阶奇异值较大，其他阶的奇异值很小。而对于信噪比较高的信号，仍然满足上述规律。

(2)每个频率成分经SVD所获得的奇异值的大小是由该频率成分的振幅决定，振幅越大，经分解后在S中所表现出的奇异值的数值越大。而奇异值的大小和频率大小无明显关系。

现构造信号y1对以上性质加以说明。y1中含有四个分量，分量1是频率10 Hz、振幅为1的正弦分量；分量2是频率为20 Hz、振幅为2的正弦分量；分量3是频率为30 Hz、振幅为3的正弦分量；分量4是均值为0、方差为1的白噪声。y1的采样频率为1 000 Hz，含有1 024个采样点。图1是y1及其各分量的时域图。

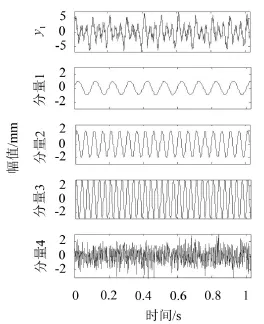
图1 y1及各分量的时域图

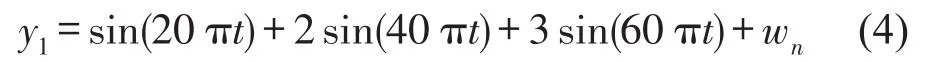
构造Hankel矩阵并对其进行SVD分解，获得U1、S1和V1。画出S1中奇异值随其所在阶数的变化火柴梗图，见图2。

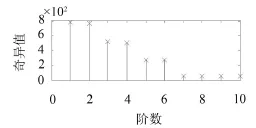
图2 奇异值-阶数变化图

从图2中可以发现：前6阶奇异值(772.34、762.55、520.89、506.16、256.98、250.05)的数值比较大，为有用信号的奇异值，而之后的奇异值很小，为噪声成分的奇异值。而且前6阶奇异值可以很明显地分成三组：772.34和762.55为一组；520.89和506.16为一组；256.98和250.05为一组。由前述的SVD的性质可得：这三组奇异值是由三个频率成分分解获得，而且这三个频率成分的振幅依次递减。再参照y1的频率组成可以确定：772.34和762.55是30 Hz分量的奇异值，520.89和506.16是20 Hz分量的奇异值，256.98和250.05为10 Hz分量的奇异值。

分别选取前三组奇异值重构出三个时间序列，图3为三个序列时域图及幅值谱。

从图3中可以明显看出三个序列各自对应着y1中的30 Hz、20 Hz和10 Hz的频率成分，和前面的结论相吻合。

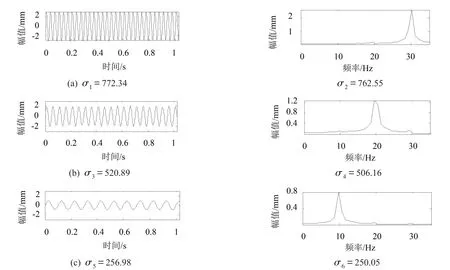
图3 三组奇异值重构出的时间序列的时域图及幅值谱

2.2 基于SVD的模态混叠消除方法

由前面的分析可知，SVD对于各频率成分的振幅敏感，只要不同频率振幅不一样，它们经SVD后得到的奇异值的大小就会存在差异。因此，可基于SVD的振幅分辨能力来消除EMD中的模态混叠现象，在不改变信号的频率成分的前提下，使得各成分振幅的大小关系变得明确。根据原信号中的频率成分由小到大依次构造出一组振幅不同的正弦信号，再将其叠加到原信号中产生一个叠加信号，该信号的频率成分与原信号的频率成分完全相同。如果每个正弦信号的振幅选取合适，就可以掩盖原信号中的各频率成分的振幅差异，使叠加信号中各频率成分振幅的大小关系和加入的正弦信号的振幅大小关系一致，进而再用SVD获取叠加信号中的每个频率成分，并减去相对应的正弦信号，即可得到原信号的分解结果。

用于研究模态混叠的原信号应满足以下两个要求：一是原信号是平稳的，平稳信号由若干个固定的频率组成且这些成分存在于整个信号区间。这样分解得到的分量才能用幅值谱的方法得到它们的频率组成；二是信号的截取应满足采样定理及信号的长度不能太短，以使原信号中的频率不发生失真及获得较高的频率分辨率。

假设x是一个经EMD分解易产生模态混叠的信号，模态混叠消除方法的具体步骤如下：

(1)从x的时域图上得到它的振幅A，从幅值谱上得到其频率成分

(2)相应地分别构造k个正弦信号

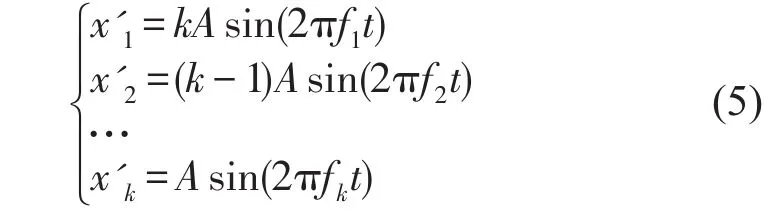
(3)把这k个信号叠加到x中。得到一个新序列xnew。

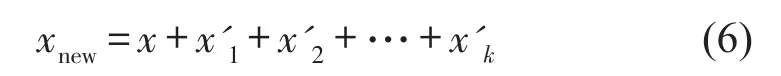
xnew中的频率成分仍然为f1、f2、···、fk，由于每个正弦信号的振幅选取为A的整数倍，即使原信号中各频率成分的振幅相差再大，也大不过A，这就保证了x'k中各频率成分的振幅的大小关系掩盖了原信号中的各频率成分的振幅大小关系，因此xnew中振幅由大到小的各频率成分依次为：f1、f2、···、fk。

(4)构造xnew的Hankel矩阵Hnew，并对其进行SVD分解，获得两个酉矩阵Unew和Vnew，一个对角矩阵Snew。

(5)依次成对选取Snew中的前2k奇异值重构出k个信号成分xb1、xb2、···、xbk。显然，xbi(i=1, 2，…，k)是叠加信号中fi对应的时间序列。

(6)从xbi中减去x'i(i=1,2，…，k)，得到原信号中fi对应的信号成分xi。

2.3 基于仿真信号性能检验

实验发现，EMD在分解含有频率成分值较接近的信号时易产生模态混叠，因此构造信号y2(见图2)，其中含有10 Hz、12 Hz和14 Hz的频率成分，且各成分振幅相等。该信号共有1 024个采样点，采样频率为1 000 Hz。

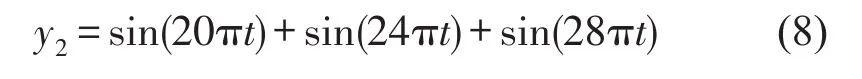
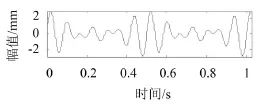
图4 y2的时域图

先对y2进行EMD分解，图5为IMF分量的时域图和幅值谱。从图5(b)中可以明显地看出IMF分量中存在着模态混叠现象，体现在IMF1中同时含有10 Hz、12 Hz、14 Hz三个频率成分；IMF1和IMF2中都含有10 Hz的频率成分。

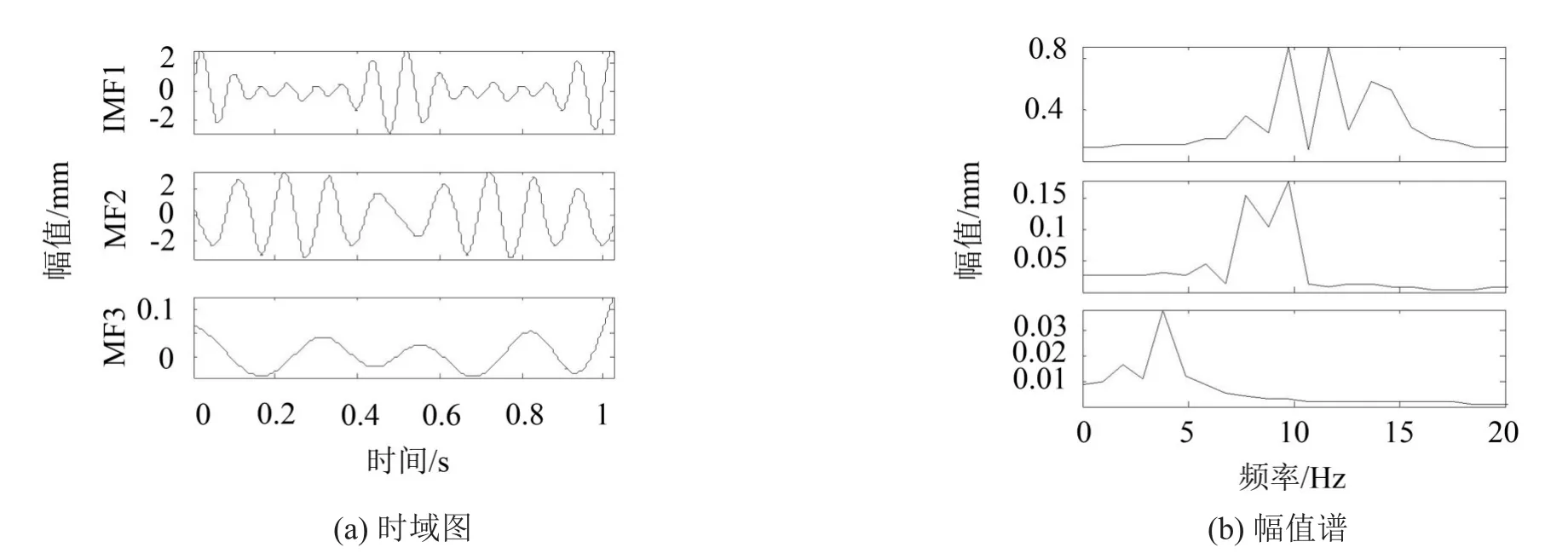
图5 IMF分量的时域图和幅值谱

下面，用基于SVD的模态混叠消除方法进行处理。

从时域图上得到y2的幅值为A2=2.93。再根据其中10 Hz、12 Hz、14 Hz的频率成分，分别构造三组正弦信号

将y2、x'1、x'2、x'3相加，得到一个新序列y2new。y2new中同样含有10 Hz、12 Hz、14 Hz的频率成分。振幅由大到小的各频率成分依次为：10 Hz、12 Hz、14 Hz。

构造y2new的Hankel矩阵H2new并对其进行SVD，并成对选取对角阵的前六个奇异值分别重构出3个序列xb1、xb2、xb3。从xbi中减去x'i，分别得到三个分量x1、x2和x3。图6为xi的时域图和幅值谱。从图6(b)中可以看出每个幅值谱明显只含有一种频率成分，不存在模态混叠现象，且各频率依次为10 Hz、12 Hz、14 Hz，和原信号中的频率成分吻合。图6(a)中xi的振幅都稳定在1处，和原信号中的各频率振幅一致。各频率成分被很好地单独从y2中分离出来。

2.4 基于实测信号的性能检验

唐宏宾等指出，在实测环境中获得的液压信号大都可以看成由噪声和若干个不同频率族分量组成，而每个频率族分量所对应的幅值可以看成调幅信号[15]，这类信号可以看成广义平稳信号，因此采用液压信号来检验所提出方法的性能。y3是一个实测液压振动信号，含有1 024个采样点，采样频率为1 000 Hz。图7是y3的时域图和幅值谱，图7(b)中较为明显的频率成分有20 Hz、40 Hz、60 Hz、175 Hz。

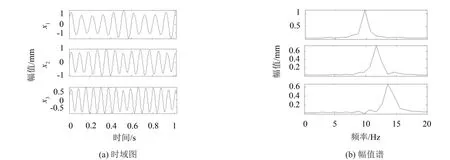
图6 xi的时域图和幅值谱

图7 y3的时域图和幅值谱

先对y3进行EMD分解，图8为IMF分量的时域图和幅值谱。从图8(b)中可以看出两点：一是分解得到的IMF分量中存在着模态混叠，IMF2中同时含有40 Hz、60 Hz的频率成分；二是IMF分量的频域图比较散乱，分量中噪声含量较高。

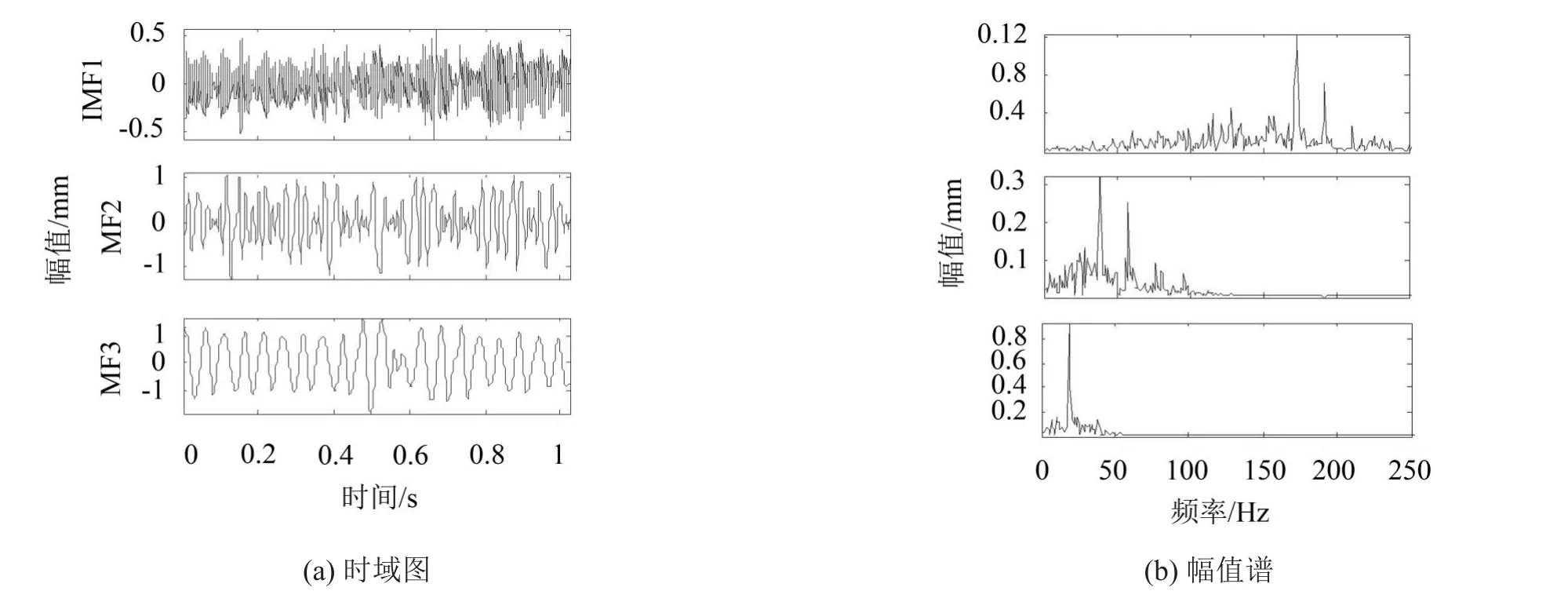
图8 IMF分量的时域图及其幅值谱

用基于SVD的模态混叠消除方法进行处理。步骤同上，得到四个时间序列x1、x2、x3和x4，图9为xi的时域图和幅值谱。图9(b)中每个幅值谱中明显只含有一种频率成分，不存在模态混叠现象，各频率成分被很好地单独从y3中分离出来。分别为20 Hz、40 Hz、60 Hz和175 Hz，和图7(b)中的主要频率成分吻合。同时各分量的频域谱线比较平滑，噪声含量比较小。

3 结语

利用SVD分解得到的奇异值对不同频率振幅大小的分辨能力，提出一种基于SVD分解的消除模态混叠的方法，通过向原信号中叠加一组单一频率的正弦信号，使得原信号中各频率模糊的振幅关系在叠加信号变得清晰。然后再利用SVD分解的振幅分辨能力将各频率成分分开。

对仿真信号和实测信号的分解实验表明，对于EMD分解容易产生模态混叠的信号，文中提出的方法能够较好地将信号中的各频率成分单独地分开，很好地消除了模态混叠的现象，改进了EMD的性能。

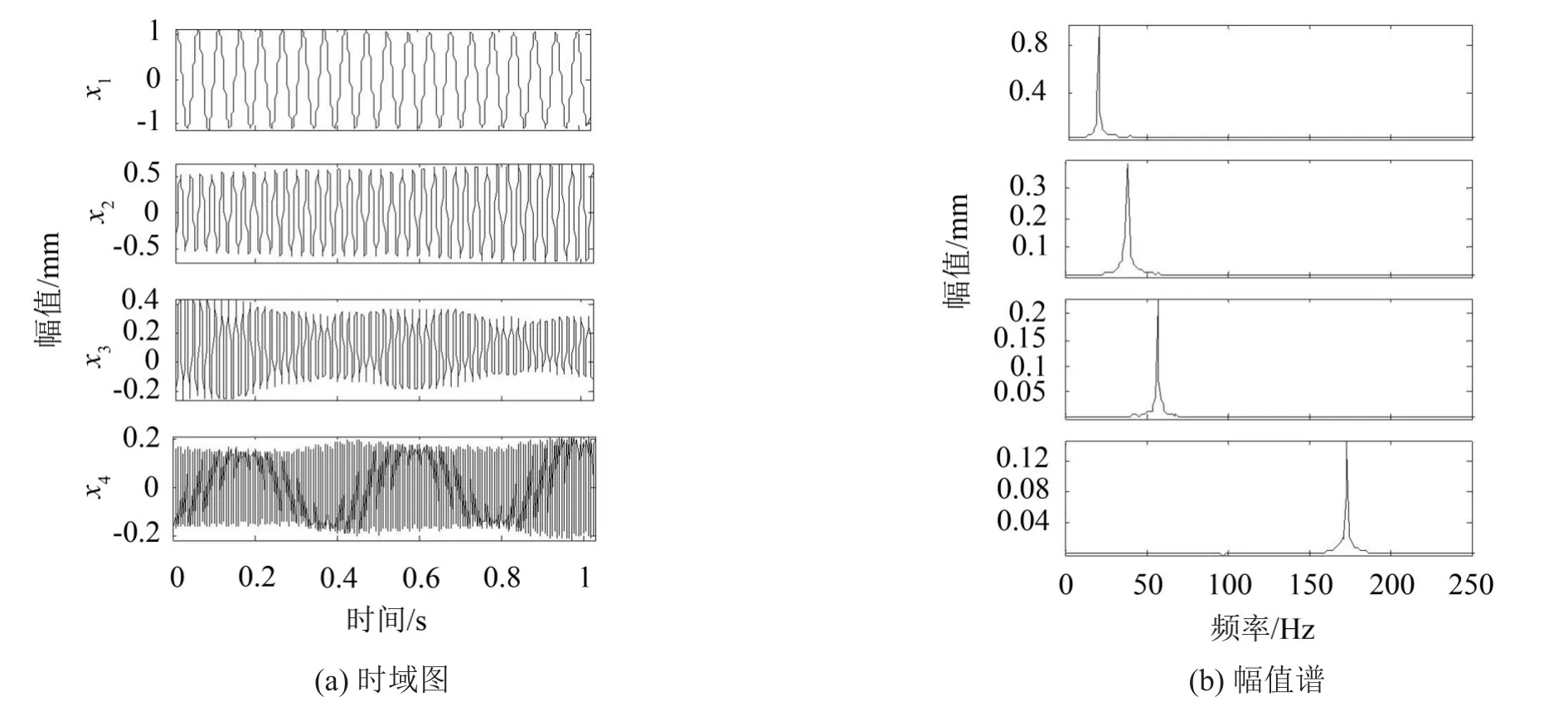
图9 xi的时域图及其幅值谱

[1]HUANG N E,SHEN ZHENG,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]. Proceedings of the RoyalSociety ofLondon A: Mathematical, Physical and Engineering Sciences. London:The Royal Society,1998.903-995.

[2]HUANG N E,WU MAN LI,QU WEN DONG,et al. Applications of Hilbert-Huang transform to non-stationary financialtime seriesanalysis[J].AppliedStochastic Models in Business and Industry,2003,19(3):245-268.

[3]WU ZHAO HUA,HUANG N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method [J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[4]邱绵浩，刘蔷，丛华.基于B样条插值曲线直接筛选的EMD及其在机械振动信号处理中的应用[J].装甲兵工程学院学报，2007，21(3)：29-33.

[5]XU ZHENG GUANG.An alternative envelope approach for empirical mode decomposition[J].Digital Signal Processing,2010,20(1):77-84.

[6]毛博，高斐，孟军.一种基于分段幂函数插值法的经验模态分解方法及其应用研究[J].中国测试，2013，39(2)：125-128.

[7]朱赛，尙伟.经验模态分解中的包络算法[J].火力与指挥控制，2012，37(9)：125-128.

[8]RYAN D,KAISER J F.The use of a masking signal to improve empirical mode decomposition[C].International Conference on Acousic,Speech and Signal Processing 2005 IEEE.MA,USA:MIT Press,2005:485-488.

[9]赵玲，刘小峰，秦树人，等.消除经验模态分解中混叠现象的改进掩膜信号法[J].振动与冲击，2010，29(9)：13-17.

[10]HASSANPOUR H,ZEHTABIAN A.Time domain signal enhancement based on an optimized singular vector denoising algorithm[J].Digital Signal Processing,2012, 22(5):786-794.

[11]刘鎏，闫云聚，李鹏博.奇异谱分解在超声速无人机声振试验数据处理中的应用[J].振动与冲击，2015(3)：28-34.

[12]王超，孔凡让，黄伟国，等.改进的奇异值分解在轴承故障诊断中的应用[J].振动工程学报，2014，27(2)：296-303.

[13]胥永刚，谢志聪，孟志鹏，等.基于奇异值分解的磁记忆信号特征提取方法[J].振动、测试与诊断，2014，34(6)：1105-1109.

[14]钱征文，程礼，李应红.利用奇异值分解的信号降噪方法[J].振动、测试与诊断，2011，31(4)：459-463.

[15]唐宏宾，吴运新，滑广军，等.基于EMD包络谱分析的液压泵故障诊断方法[J].振动与冲击，2012，31(9)：44-48.

An EMD ModeAliasing Elimination Method based on SVD

ZHANG Xiao-ming1,TANG Jian1,HAN Jin2
(1.Engineering Institute of Engineering Corps,PLAUniversity of Science and Technology, Nanjing 210007,China; 2.Logistics Center,Northwest Industry Group Co.Ltd.,Xi'an 710043,China)

An EMD mode aliasing elimination method is proposed based on SVD.The SVD has two features:(1)each frequency component corresponds to two sizeable singular values after decomposition;(2)these singular values have a positive correlation with the frequency.According to the major frequency components of the original signal,a series of sinusoidal signals are constructed whose frequencies are the same as those of the original signal but the amplitudes are integer times of those of the original signal.Then,these sinusoidal signals are superimposed with the original signal and the new signal is decomposed by SVD.Selecting the singular values in pairs from the decomposed new signal,another series of signals is reconstructed.The final decomposition results are achieved by subtracting the corresponding sinusoidal signals from the reconstructed signals.Experiments show that this method can eliminate the mode aliasing effectively even when the frequency components are close in the signal.

vibration and wave;EMD;mode aliasing;SVD;signal construction

TH137

：A

：10.3969/j.issn.1006-1335.2016.06.028

1006-1355(2016)06-0142-06

2016-04-10

国家自然科学基金资助项目(51175511，61472392)；江苏省青年基金项目(BK20150724)

张小明（1991-），男，江苏省南通市人，硕士生，主要研究方向为信号处理、机械故障诊断。E-mail:18761682069@163.com

唐建，女，讲师，主要研究方向为信号处理、机械故障诊断。