基于车桥耦合的高架槽形梁结构噪声影响分析

曾 峰，刘林芽，吴宇鹏，宋 瑞

（华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌 330013）

基于车桥耦合的高架槽形梁结构噪声影响分析

曾 峰，刘林芽，吴宇鹏，宋 瑞

（华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌 330013）

为了探讨列车通过轨道交通高架槽形梁时诱发的结构噪声，以某拟建30 m轨道交通槽形梁为研究对象，建立车桥耦合系统振动分析模型以及槽形梁结构声辐射有限元/边界元模型。采用多体动力学软件Simpack建立列车的空间动力学模型，采用有限元软件Ansys建立槽形梁有限元模型，基于Simpack和Ansys相结合的联合仿真方法，获取轮轨激振力。在计算列车荷载作用下槽形梁结构振动响应的基础上，采用有限元-间接边界元耦合声学分析法，探讨底板厚度以及腹板高度对槽形梁结构噪声的影响。研究结果表明：底板厚度的增加可以降低槽形梁梁体正下方的结构噪声，但并非越厚越好，底板厚度对结构远声场有一定程度的影响，但降噪效果不明显；腹板高度的变化使槽形梁结构噪声辐射衰减方向有所改变，桥梁腹板两侧噪声辐射衰减速度较快；桥梁底板正上方的结构辐射噪声最强区域有缩小趋势；分析结果可为轨道交通槽形梁结构减振降噪优化设计提供一定的理论参考依据。

振动与波；耦合振动；联合仿真；结构噪声；有限元；间接边界元

大力发展轨道交通是解决城市交通拥挤最有效的途径之一[1]，但是高架结构的振动与噪声影响已成为制约城市轨道交通发展的重要因素[2]。因此，研究轨道交通高架桥梁结构辐射噪声的影响，对于选择合理的减振降噪措施、优化桥梁结构设计、促进交通行业的发展具有重要意义。

轨道交通高架桥梁在列车荷载的作用下诱发振动，并向周围环境辐射噪声，其中0～100 Hz频段的噪声属于低频噪声[3-4]。而低频噪声具有绕射能力强、衰减较慢等特点，并且该频段噪声对人体有长期性危害，因此有必要针对轨道交通槽形梁的结构噪声展开研究[5]。

影响轨道交通槽形梁结构辐射噪声的因素很多，桥梁结构形式、结构参数、结构刚度等均可对桥梁结构的声辐射特性产生影响。张迅、李小珍等通过对简支梁结构噪声的理论分析和试验测试，研究发现板厚是影响结构噪声的重要参数[6]。韩江龙、吴定俊等采用模态叠加法分析了桥梁的结构噪声和不同构件的声压贡献量，研究发现增加底板的厚度可以降低梁底的结构噪声[7]。但方小华，古爱军等研究发现：桥梁底板厚度的变化对桥梁各个板件的振动、噪声无明显影响，腹板厚度的变化对桥梁的振动和噪声影响较小[8]。Bewes通过对不同桥梁结构进行研究，发现桥梁某些结构组件厚度的增加，可以降低这一组件的结构噪声，但同时会增加其他组件的结构噪声[9]。因此，板厚对槽形梁结构噪声的影响亟待进一步分析研究。

工程实践中，高架槽形梁因其自身构型的特殊性，两侧的腹板具有阻隔轮轨噪声的功能，同时大量减少了高架轨道声屏障的使用[10]。但腹板结构高度对综合辐射声场的影响少见文献报道。

文中以某拟建30 m的简支槽形梁为研究对象，基于Simpack和Ansys相结合的联合仿真方法，建立车桥耦合系统振动分析模型以及槽形梁结构声辐射有限元/边界元模型，获取轮轨激振力，在计算列车荷载作用下槽形梁结构振动响应的基础上，采用有限元-间接边界元耦合声学分析法，探讨了底板厚度以及腹板高度对槽形梁结构噪声的影响。

1 轨道交通槽形梁振动声辐射计算模型

1.1 轨道交通高架槽形梁桥模型

某轨道交通集团拟建高架段为平坡线路，拟采用双线分离式结构，桥的结构类型为槽形梁，桥墩为T型墩，如图1所示。

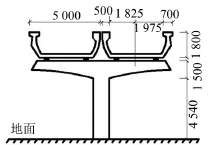
图1 拟建高架槽形梁桥梁截面（单位/mm）

槽形梁的标准跨径为29.94 m，梁宽为5 m，高为1.8 m，底板厚度为0.28 m，腹板厚度为0.24 m，支座设在距梁端0.57 m处。

1.2 轨道交通槽形梁有限元模型

基于有限元理论，建立轨道交通槽形梁模型。在分析模型中，所有材料均处于线弹性阶段，将钢轨视为Euler梁，用梁单元模拟；槽形梁梁体、轨道板、CA砂浆层均用实体单元模拟，为避免病态网格的出现，采用体扫掠法将其划分为大小合适的六面体单元；连接钢轨与轨道板的扣件系统采用间距为0.625 m的离散弹簧阻尼单元模拟，主要结构参数见表1。

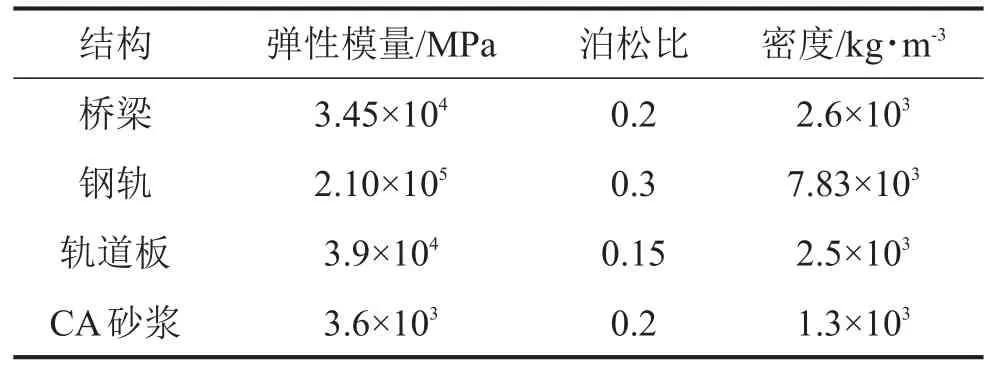
表1 槽形梁模型主要结构参数表

槽形梁的截面形式参照某拟建轨道交通选用的简支槽形梁设计图纸，梁体腹板一侧为圆弧结构、另一侧采用折腹线式直线的不对称结构，有限元模型如图2所示。

图2 轨道交通槽形梁有限元模型

各项参数经过多次调试，能满足GB50157-2013地铁设计规范的要求[11]。

1.3 轨道交通槽形梁边界元模型

基于流体介质的守恒原理和关于声波动的一些基本假设，采用变量分离法，由三维波动方程可知槽形梁声辐射的Helmholtz方程表达式如下

式中Δ2为拉普拉斯算子；k=ω/c为声波波数；c为空气介质中的声速；ω为圆频率；p为声场任意点的声压。

槽形梁结构振动体表面的运动可认为是小振幅的，其属于不渗透边界，边界条件为

式中vn表示表面法向振速；n表示桥梁结构振动体表的外法线；ρ表示流体密度；i表示虚数单位。

基于边界条件，利用加权残值法，可得到式（1）的基本解，为

式中QX表示结构表面上任意点，QY表示声场中的任意点。

确定边界元两侧的声压差和声压梯度差，然后将Helmholtz积分方程应用于边界表面两侧，即可获得声场中任意场点的声压

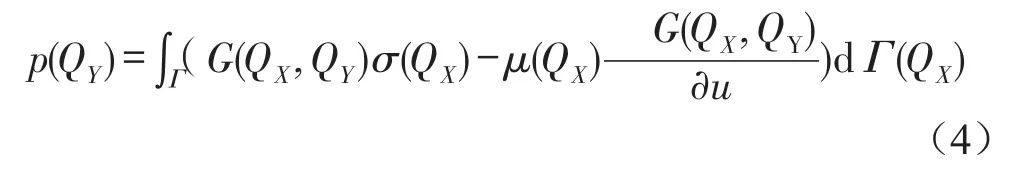
式中σ（QX）、μ（QX）分别表示QX点桥梁结构表面两侧振速差和声压差。Γ表示边界表面。

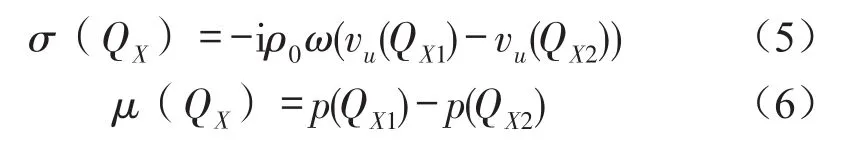
式中ρ0为空气密度；vu(QX1)、vu(QX2)分别表示桥梁结构表面上任意点QX两侧的法向振速；p(QX1)、p(QX2)分别表示桥梁结构表面上任意点QX两侧的声压。

利用边界单元离散化桥梁结构表面，可得到桥梁结构表面边界上每个节点的两侧振速差和声压差为

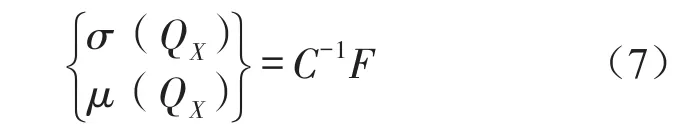
式中C表示对称的复数满秩矩阵；F表示荷载激励向量。

由式（7）可得槽形梁结构声场外任意点QY处的声压

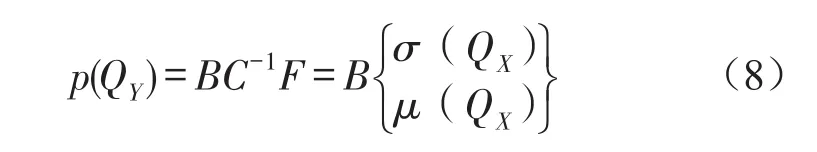
式中B表示复数满秩矩阵，与结构的表面形式等有关。

基于有限元-间接边界元耦合声学理论，建立了高架槽形梁边界元模型。在建立声学边界元模型时，考虑最大单元的边长要小于计算频率最短波长的1/6，即最大单元的边长要满足如下表达式

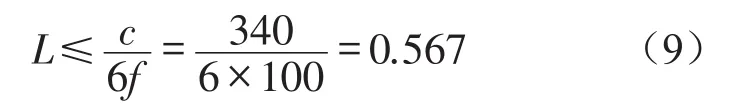
式中c表示为声速，取340 m/s。采用间接边界元法计算桥梁结构振动声辐射情况时，槽形梁边界元网格划分最大单元尺寸为0.312 5，满足式（9）。槽形梁边界元网格如图3所示。

图3 轨道交通槽形梁边界元模型及场点网格

1.4 车桥耦合模型

为了避免车桥耦合振动分析交叉迭代计算量较大的弊端，基于多体动力学理论，建立精细化车桥耦合的空间动力学分析模型。地铁列车模型的结构参数及动力学参数参照实际地铁B型车选取，在作一些简化的基础上，通过Simpack建立。其中每一节地铁车辆动力学分析模型可以认为由1个车体、2个转向架（含4个轮对）等刚体组成，每一节刚体车辆考虑了伸缩、横摆、浮沉、点头、测滚、摇头6个自由度，每一节车辆共考虑34个自由度。轮对和转向架以及转向架和车体之间分别通过一系、二系弹簧连接；轮轨接触采用单点非线性弹性接触；轨道不平顺选用美国6级不平顺谱。列车基本参数见表2。

表2 列车基本参数

将基于有限元软件Ansys建立的槽形梁有限元模型作为柔性体导入多体动力学软件Simpack中，同时，导入槽形梁模态分析和子结构分析的结果文件。利用Simpack中柔性轨道模块，实现列车模型和桥梁模型的共同求解。其中，将列车模型和槽形梁有限元模型分别作为两个系统，分别求解轮流迭代。车桥耦合模型之间通过轮轨接触离散点实现位移、速度、作用力的交换。为了控制车辆系统和桥梁系统所有自由度的计算结果相对于前一迭代步的误差都不超过系统迭代控制误差精度的要求，文中控制精度取10-4。车桥耦合模型如图4所示。

图4 车桥耦合模型

2 轮轨激振力的获取和加载

基于车桥耦合模型，采用联合仿真法,模拟轮轨之间的相互作用力。采用地铁车辆6节编组模拟加载，计算速度为80 km/h。最终得到轮轨垂向作用力。

将列车实际运行过程简化为一系列随时间移动的集中力荷载，采用节点加载方式分析高架槽形梁的结构噪声辐射特性，每节车辆按轮对左右对称分布共8个集中力荷载，加载时间步长为0.005 s，加载方式如图5所示。

图5 轮轨激振力加载方式

3 结构噪声的影响参数分析

3.1 轨道交通槽形梁原模型声辐射分析

将基于车桥耦合模型计算出来的轮轨激振力加载到轨道-槽形梁有限元模型上，进行轨道交通槽形梁的瞬态动力响应分析，再以轨道交通槽形梁动力响应结果作为边界条件，采用声学间接边界元法进行轨道交通槽形梁结构噪声预测分析。

为了研究距桥体中心线水平向不同距离处槽形梁的声场分布规律，沿水平方向分别选取5个场点进行分析。图6为高架槽形梁声场输出场点分布图，场点1至场点5距地面2 m，距线路中心线的水平距离分别为0 m、5 m、10 m、20 m、25 m。

图6 高架槽形梁声场输出场点分布图

由图7槽形梁场点线性声压级1/3倍频图可知，轨道交通槽形梁结构噪声辐射的优势频段基本处在20 Hz～80 Hz，峰值频率都出现在31.5 Hz和63 Hz附近，这主要源于桥梁振动加速度响应在31.5 Hz附近有一个峰值，而对于最大峰值频率63 Hz，通过考察槽形梁的模态特征，发现在中心频率63Hz附近对应有一个振动模态，固在63 Hz处出现最大峰值频率。这与文献[7]中实测峰值频段具有很好的一致性。

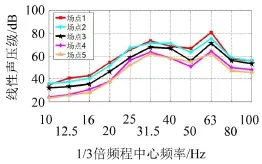
图7 槽形梁场点线性声压级1/3倍频程曲线

3.2 底板厚度对结构噪声的影响分析

以拟建30 m标准跨径槽形梁为标准模型，通过改变底板厚度或者改变腹板的高度，得到其他模型，结构示意图如图8所示。

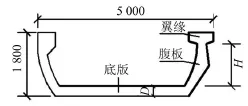
图8 槽形梁结构截面示意图（单位/mm）

其中板件厚度和高度满足《混凝土结构构造手册》的要求[12]。

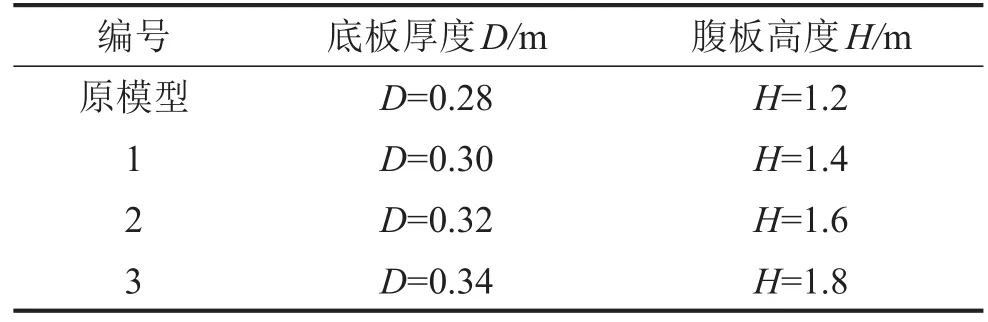
表3 槽形梁模型参数表

鉴于槽形梁结构噪声主要集中在100 Hz以下，同时，为了避免A计权对低频噪声的削弱，因此选取10 Hz～100 Hz频率范围内的声场点处线性声压级来分析结构底板厚度对槽形梁辐射噪声的影响。图9给出了不同声学场点10 Hz～100 Hz频段内线性声压级最大值。

由图9可知，从槽形梁跨中正下方场点1到场点3，槽形梁壁板厚度的变化对梁体结构噪声的控制有一定效果，随着底板厚度的增加，结构辐射的噪声降低，但减少量随板厚的增加而逐渐减小，这是由于槽形梁底板直接承受列车荷载的作用，其厚度的增加，结构底板的抗弯刚度增大。

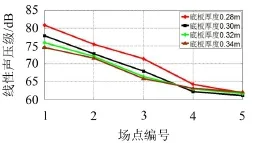
图9 不同声学场点线性声压级最大值

在距桥梁中心线20 m、25 m处的场点4、场点5，随着底板厚度的增加，其线性声压级最大值降低不明显，甚至有升高的现象，这是由于随着底板厚度的增加，其结构质量、辐射面积增大，噪声的辐射效率同时增大，造成了底板厚度为0.34 m时，出现场点线性声压级最大值升高现象，说明通过底板厚度的变化控制槽形梁结构噪声的措施是适当的。

由图9可以发现，槽形梁结构噪声辐射规律较为复杂。同时，为了进一步表征在各个频段内，槽形梁底板厚度的变化对桥梁结构噪声辐射的影响，在分析各个场点的1/3倍频程中心频率处的最大线性声压级基础上，利用声压级累计叠加原理，计算各个场点在10 Hz～100 Hz频段内的总体线性声压级。

由图10可知，底板厚度的增加对梁体正下方具有较好的降噪效果，但并非越厚越好，底板厚度增大到0.34 m时，出现了声压级的增大现象；在距离桥体中心线20 m～25 m的远声场，板厚的增加对远声场的辐射噪声降低不明显。

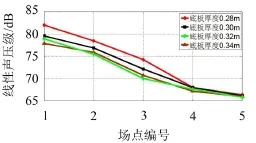
图10 不同声学场点总体线性声压级

3.3 腹板高度对结构噪声的影响分析

图11和图12分别描述了槽形梁原模型与腹板加高0.6 m两种工况下跨中截面在63 Hz峰值频率下的二维声场分布情况。

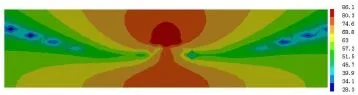
图11 槽形梁原模型跨中断面声压分布云图（f=63 Hz，单位/dB）

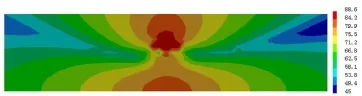
图12 槽形梁腹板加高0.6 m后跨中断面声压分布云图（f=63 Hz，单位/dB）

由图11可知，槽形梁在63 Hz峰值频率下，底板的振动诱发的噪声辐射声压值较高，声能量主要集中在底板正上方和正下方区域；槽形梁结构噪声辐射在桥面板下方衰减较慢；地面附近由于地面对声波的反射，辐射声压出现放大现象；沿着桥梁底板上方45°左右方向衰减较快，图中表现为云图颜色变化明显。

由图12可知，槽形梁腹板两侧的场点声压在63 Hz峰值频率下结构辐射噪声衰减较快。与图11对比发现，随着槽形梁腹板高度的增加，底板正上方的结构辐射噪声最强区域有缩小趋势，体现了槽形梁的遮蔽效应；桥梁腹板两侧噪声辐射衰减较快；同时，腹板高度的增加使槽形梁综合声场结构噪声辐射衰减方向有所改变，图中表现为云图颜色变化明显。

4 结语

基于Simpack和Ansys相结合的联合仿真方法，建立车桥耦合系统振动分析模型以及槽形梁结构声辐射有限元/边界元模型。在计算列车荷载作用下槽形梁结构振动响应的基础上，采用有限元-间接边界元法耦合声学分析法探讨了底板厚度以及腹板高度对槽形梁结构噪声的影响。通过数值分析得到以下结论：

（1）列车以80 km/h的速度运行在高架桥梁上时，轨道交通槽形梁结构噪声辐射以20 Hz～80 Hz低频为主，最大峰值都出现在63 Hz附近。

（2）高架槽形梁底板厚度的增加对梁体正下方具有较好的降噪效果，但并非越厚越好；对结构远声场，有一定程度的影响，但降噪效果不明显。

（3）高架槽形梁腹板高度的增加使槽形梁综合声场结构噪声辐射衰减方向有所改变；桥梁腹板两侧噪声辐射衰减较快；桥梁底板正上方的结构辐射噪声最强区域有缩小趋势。

[1]刘加华，练松良.城市轨道交通振动与噪声[J].交通运输工程学报，2002(1)：29-33.

[2]高飞，夏禾，安宁.北京地铁5号线高架结构的辐射噪声分析与实验研究[J].中国铁道科学，2010(5)：134-139.

[3]刘林芽，许代言.腹板开孔的箱型梁结构噪声辐射特性分析[J].振动与冲击，2016，35(15)：204-210.

[4]谢旭，张鹤，山下幹夫，等.桥梁振动辐射低频噪声评估方法研究[J].土木工程学报，2008(11)：53-59.

[5]宋晓东，吴定俊，李奇.基于无限元的2.5维方法预测轨道交通混凝土桥梁低频噪声[J].振动工程学报，2015，28 (6)：929-936.

[6]张迅，李小珍，刘全民，等.混凝土箱梁的结构噪声及其影响因素[J].西南交通大学学报，2013，48(3)：409-414.

[7]韩江龙，吴定俊，李奇.板厚和加肋对槽型梁结构噪声的影响[J].振动工程学报，2012，25(5)：589-594.

[8]方小华，谷爱军，吴建峰.轨道交通简支箱梁桥振动传递特性分析[J].都市快轨交通，2013，26(3)：84-88.

[9]Bewes O G.The calculation of noise from railway bridges and viaducts[D].University of Southampton,2005.

[10]马军旺.城市轨道交通高架线环境景观适应性探讨[J].都市快轨交通，2015，28(6)：132-137.

[11]GB 50157-2013地铁设计规范[S].北京：中国建设工业出版社，2013.

[12]王文栋.混凝土结构构造手册（第四版）[M].北京：中国建筑工业出版社，2012.

Analysis for the Structure Noise of Simply Supported Trough Girders Considering Vehicle-bridge Vertical Interaction

ZENG Feng,LIU Lin-ya,WU Yu-peng,SONG Rui
（Engineering Research Center of Railway Environmental Vibration and Noise, Ministry of Education,East China Jiaotong University,Nanchang 330013,China)

The structure noise of simply-supported trough girders in urban rail transit is analyzed.The model of vehiclebridge coupling system for a 30 m reinforced concrete trough girder is built,and the corresponding finite element model and the acoustic boundary element model are established.The train’s spatial dynamics model is established by means of Simpack software,and the finite element model of the girder is established by Ansys software.Based on the combination of Simpack and Ansys codes,the wheel/rail exciting force is obtained.On the basis of calculating the vibration response of the trough girder under the action of train load,and using finite element-indirect boundary element hybrid acoustic analysis method,the influence of the bottom plate thickness and height of the web on the trough girder structure noise is discussed.The results show that increase of the thickness of the bottom plate can reduce the structure noise of the trough girder,but it does not mean that the thicker the bottom plate is,the better the noise reduction effect is.When the thickness of the bottom plate reaches a certain value,its influence on the noise reduction effect of the structure is limited.Variation of the web height can alter the direction of radiation attenuation of the bridge structure noise,and the structure noise radiation on both sides of the bridge attenuates fast.The radiation noise of the structure above the bottom plate is the strongest,but it has a tendency to decrease with the variation of the web height.The results of the analysis can provide some theoretical references for the optimal design of the rail transit trough beam structure.

vibration and wave;coupled vibration;joint simulation;structure noise;finite element;indirect boundary element

U491.91；U270.16

：A

：10.3969/j.issn.1006-1335.2016.06.026

1006-1355(2016)06-0131-05

2015-10-25

国家自然科学基金资助项目（51268014，51578238)；江西省“赣鄱英才555工程”领军人才培养计划资助项目

曾峰（1992-），男，湖南邵阳人，硕士研究生，主要研究方向为铁路环境振动与噪声。E-mail:316058254@qq.com

刘林芽（1973-），男，教授，博士，博士生导师。