有界窄带激励柴油机轴系扭振系统主参数共振

杨志安，卞雅媛

（1.唐山学院 唐山市结构与振动工程重点实验室，河北 唐山 063000；2.华北理工大学 机械工程学院，河北 唐山 063000）

有界窄带激励柴油机轴系扭振系统主参数共振

杨志安1，卞雅媛2

（1.唐山学院 唐山市结构与振动工程重点实验室，河北 唐山 063000；2.华北理工大学 机械工程学院，河北 唐山 063000）

研究柴油机轴系扭振强非线性系统在有界窄带激励下的主参数共振响应和稳定性问题。应用改进多尺度法得到在有界窄带随机激励下柴油机轴系扭振系统的幅频响应方程，导出系统的Ito随机微分方程。通过矩法得到系统随机均方响应的近似表达式，分析各个参数对柴油机轴系扭振系统主参数共振均方值的影响。结果表明，主参数共振稳态解稳定的充分必要条件与系统二阶矩稳定的充分必要条件是一样的；随着阻尼值的增大，系统主参数共振振幅的均方值减小；随着曲轴扭转刚度的减小，系统主参数共振的均方响应曲线的斜率增大；随着随机扰动强度的增大，系统时间响应曲线和相图变化微小。

振动与波；柴油机轴系扭振系统；窄带激励；改进多尺度法；主参数共振；均方响应

船用柴油机轴系扭转振动是影响船舶安全运行和舒适运行的重要因素。严重的扭转振动会造成曲轴、中间轴、螺旋桨轴断裂，齿轮磨损，噪声过大等危害，这些危害将影响船舶的安全航行。随着大功率船用柴油机在大型船舶的应用，轴系扭振状态也更加复杂，因此船用柴油机轴系扭振的研究变得更加重要[1]。

文献[2]研究了柴油机扭振机理和传动轴系扭振机理，并提出了针对船舶轴系的扭振测量方法。文献[3]研究了柴油机轴系受气体冲击力与水冲击动力作用的非线性扭转振动问题，通过多尺度法得到了在飞轮匀速运转条件下柴油机轴系受水冲击动力引起的主参数共振的幅频响应方程。文献[4]应用拉格朗日方程，得到柴油机轴系受膨胀气体冲击力作用的非线性扭转振动微分方程。根据多尺度法，得到主参数共振的幅频响应曲线。文献[5]研究了Duffing振子在窄带随机噪声激励下的主共振响应和稳定性问题。应用多尺度法得出了系统的阻尼项、随机项等对系统响应的影响，文献[6]研究环形极板机电耦合系统的强非线性问题，建立环形极板机电耦合系统的动力学方程，应用改进多尺度法求得系统的主共振的幅频响应曲线，分析了不同的系统参数对共振的影响。

在以上柴油机轴系扭振系统的研究中，对确定激励下的弱非线性振动问题进行了分析，但没有考虑随机激励对柴油机轴系扭振强非线性系统的影响，而实际上外激励存在相位、幅值的微小随机变化。采用有界噪声模型化窄带随机激励特征，运用改进多尺度法分析窄带随机激励作用下的主参数共振，得到系统随机均方响应的近似表达式，分析比较其中各元素对均方值与共振区间的影响，对柴油机轴系扭振系统的设计与优化具有一定的参考价值。

1 柴油机轴系扭振系统非线性动力学方程

柴油机轴系单自由度系统由飞轮、气缸及曲轴三部分组成，如图1所示。

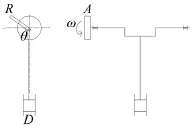
图1 柴油机轴系简图

其中A为飞轮；M表示往复部分总质量，I为气缸连杆旋转部分总转动惯量，ρ为阻尼，扭转角为θ；飞轮转动惯量为I1，曲柄半径为R；气缸直径为D；飞轮的角速度为ω,角位移为θ1=ωt，曲轴角位移为θ=ωt+γ；曲轴扭转刚度为μ；柴油机轴系扭振系统所受干扰力为膨胀气体对活塞的冲击力矩Ksin(nθ1+φ)，其中φ为冲击力矩相位角[7]，K为简谐力矩幅值，n为简谐次数（即简谐力矩在曲轴一转时间里的变化周期数）；柴油机的转速为N。

柴油机轴系模型如图1所示，根据拉格朗日方程可以建立其非线性动力学方程[8-9]，但分析系统的主参数共振时，不考虑外激励项影响，因此系统主参数共振的非线性动力学方程为[10]

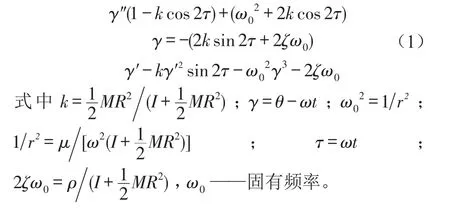
2 主参数共振分析

应用改进的多尺度法研究V≥0且远小于1时的情形。多尺度法已广泛应用于确定激励振动问题的研究中，近几年在随机振动问题中也有一定的应用[11-13]。故式（1）变为

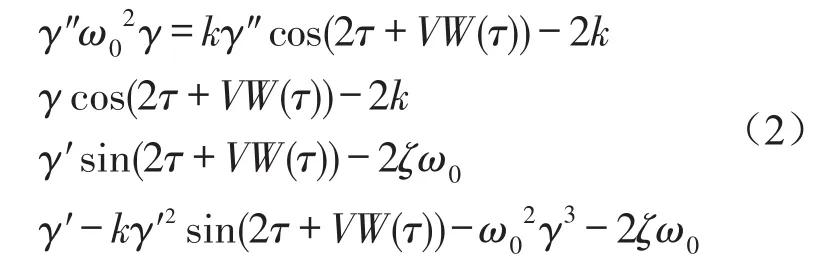
式中W(τ)为标准的Winner过程，V为随机的扰动强度。

在式（2）中各参数激励项和非线性项前引入非小量参数ε，方程变为

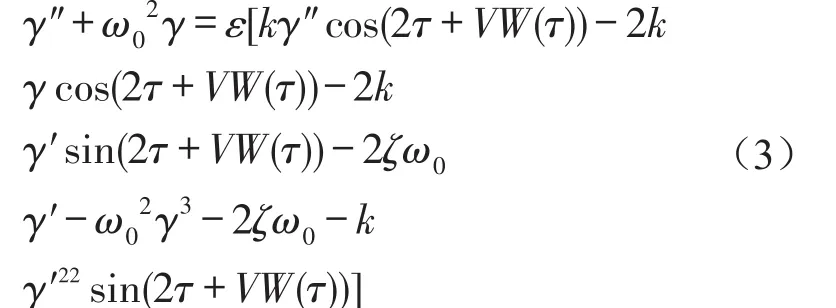
设Ω=2

令

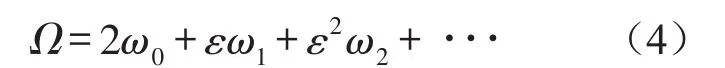
引入参数变换

则有

把小参数α引入到多尺度方法中，设式（3）的一次近似解为

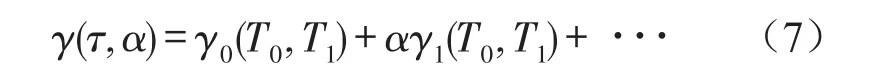
将式（6）、式（7）代入式（3）后，比较α同次幂系数，可得到消除永年项的条件，并根据欧拉公式分离实虚部可得

式（8）的精确解可以采用摄动法求得，但V很小，这里假设V=0，则式（8）变为

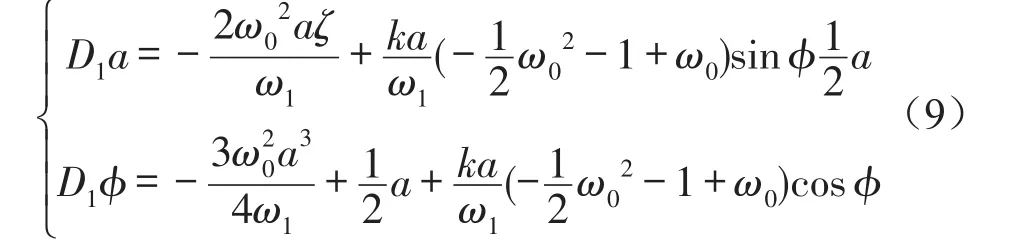
对于稳态振动a=a0，φ=φ0，有D1a=D1φ=0。可得系统表达式（9）的幅频响应方程

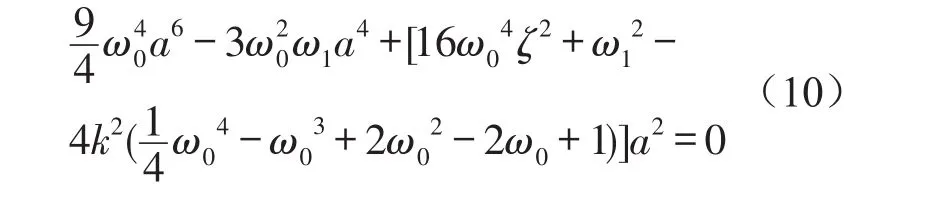
式中ω1为调谐值。

3 V≠0时稳定性条件

当V≠0时，由于V很小，可设方程式（8）的解为

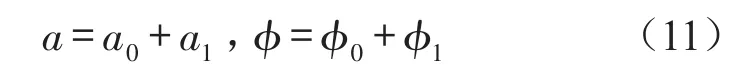
把D1a=D1φ=0代入式（9）可得a0和φ0，其中a1和φ1是摄动项，把式（11）代入式（8）中，不计关于a1和φ1的高阶项，便得方程式（8）在定常解（a0，φ0）的线性方程为

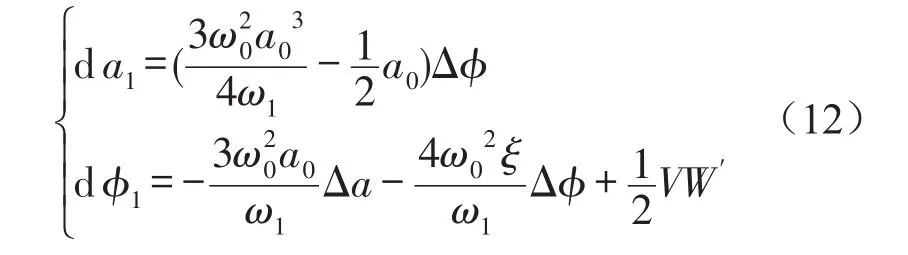
式中Δa为振幅扰动量；Δφ为相位扰动量；Wiener过程的导数W′是白噪声的另一种表示方式，所以此方程组相当于线性系统在白噪声外激励下的响应问题。

依据Hurwitz定理可知[14]，该线性系统稳定的充要条件为

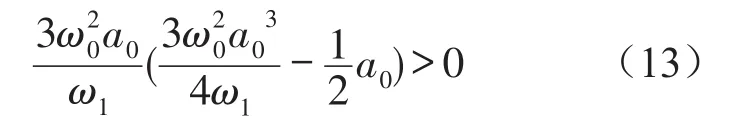
式（12）可写成对应的Ito微分方程

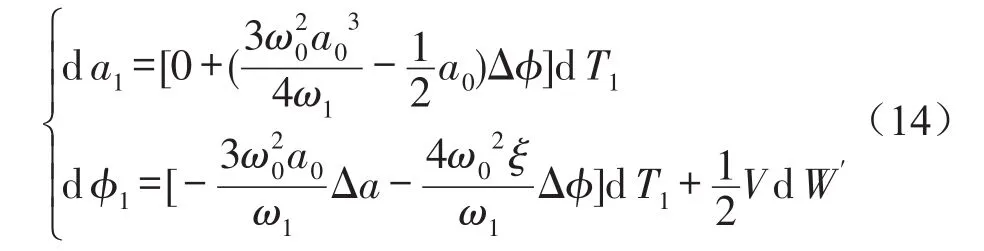
可用矩法求出式（14）的1阶矩为

式（14）可写成如下形式

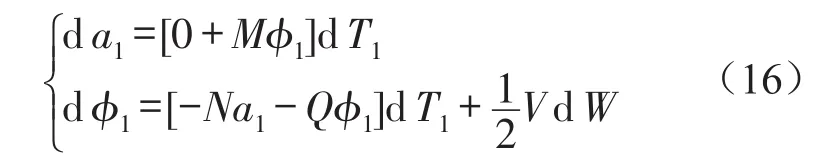
式中

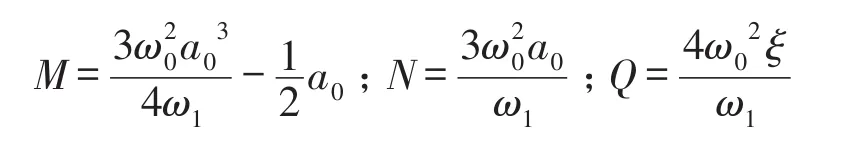
以下各式中M、N和Q同上。

由Ito微分法则可得

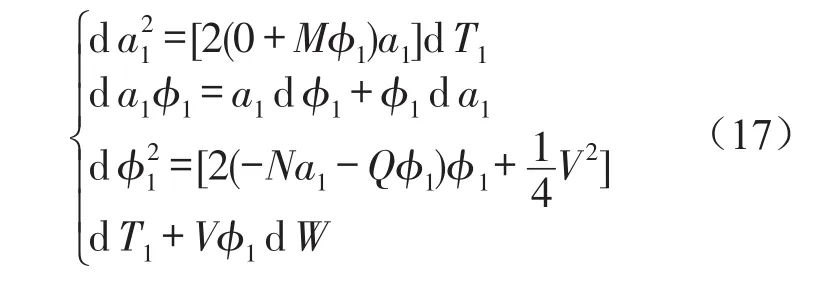
整理式（17）得

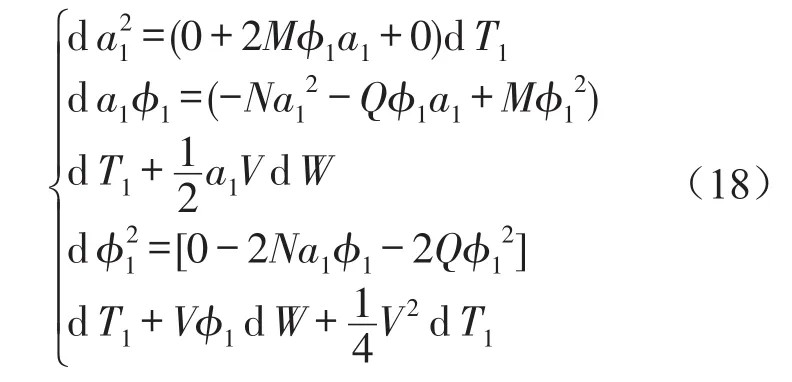
式（18）两边分别取期望，根据Ito微分法则可知

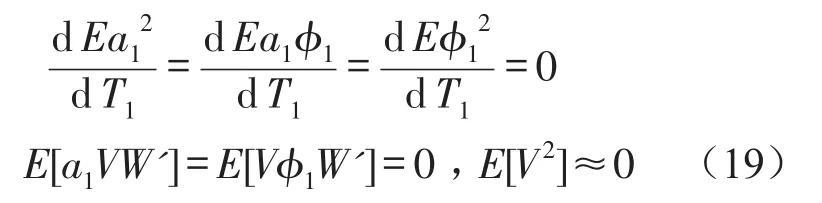
则式（18）可转化为

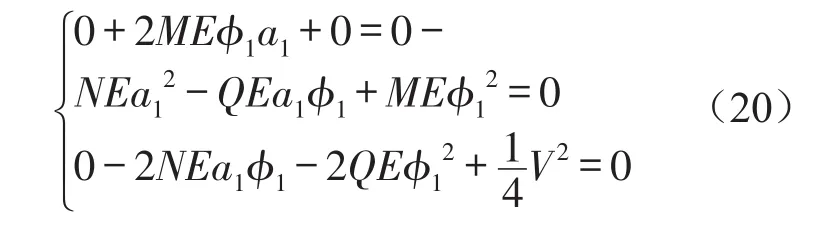
根据式（20）可知其系数矩阵为

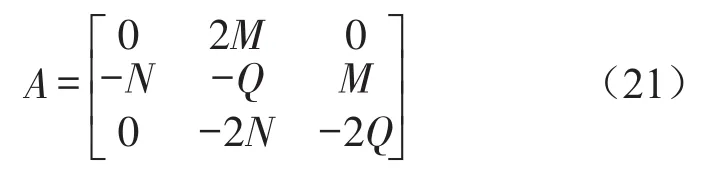
则

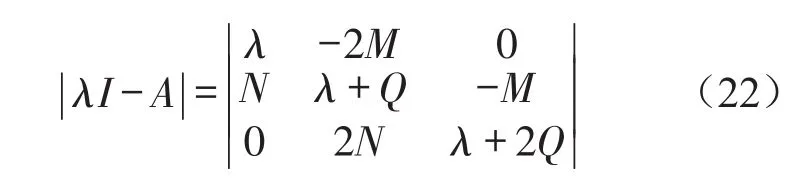
式（22）的特征方程为

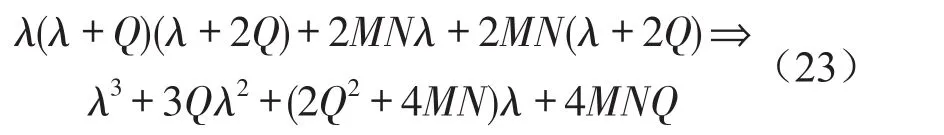
由式（23）可知

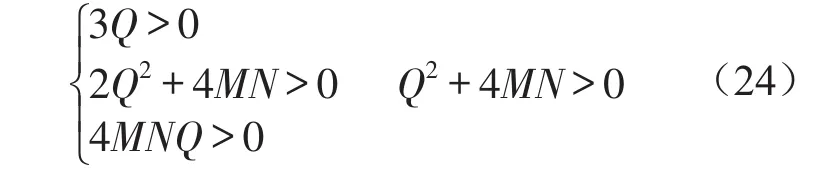
式（24）即为2阶矩存在的充分必要条件，并与前面确定性系统（13）周期解的稳定性条件一致。a0的值与Ea2的值是相互对应的。

由式（20）可一次求得Ea12、，Ea1φ1、Eφ12的值

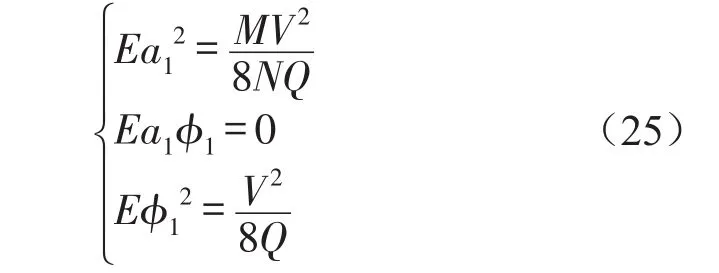
结合式（11）、式（15）和式（25）可得

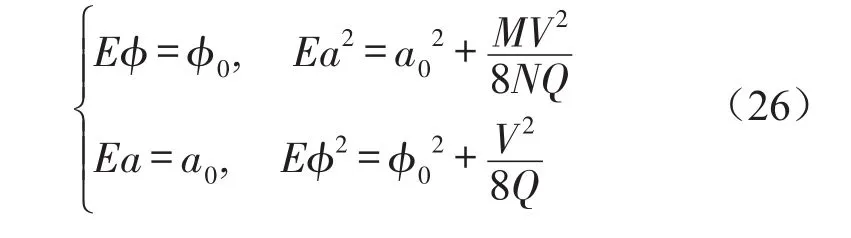
4 数值模拟

S195型柴油机数值模拟采用的参数取值如下：M=1.995 kg，I=0.088 kg·m2，D=95 mm，R=57.5 mm，得出系统的响应。

图2为V=0系统主参数共振的幅频响应曲线，由于式（2）中的项系数相同，属于强非线性问题，该曲线有两个分支解。

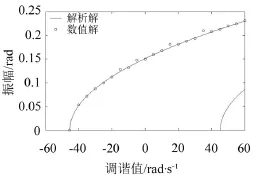
图2 幅频响应解析解和数值解的对比

一般龙格库塔只能求时域信息，通过捕捉不同频率下时域信息稳态解的振幅可以得到幅频响应解，数值解与解析解进行对比，由图2可得，数值解与解析解基本吻合。

图3为柴油机轴系扭振系统主参数共振的均方响应曲线。由图3可知，窄带随机激励下主参数共振系统均方响应曲线与系统稳态解时幅频响应曲线的拓扑结构相同，图中粗实线部分为稳定解，细实线部分为不稳定解。

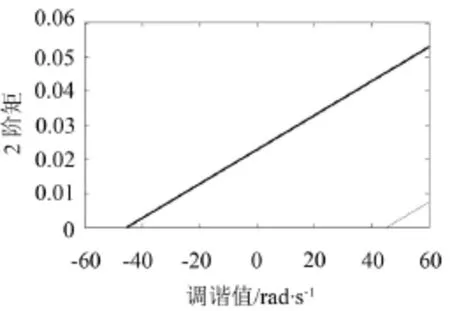
图3 均方响应曲线

图4为柴油机轴系扭振系统主参数共振在不同ρ值时的均方响应曲线。由图4可知，随着系统阻尼值的增大，系统主参数共振的均方值减小。

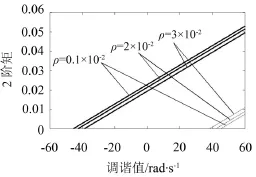
图4 不同ρ值情况下均方响应曲线

图5为柴油机轴系扭振系统主参数共振在不同μ值时的均方响应曲线。由图5可知，随着系统刚度值的减小，系统主参数共振的均方响应曲线的斜率增大。

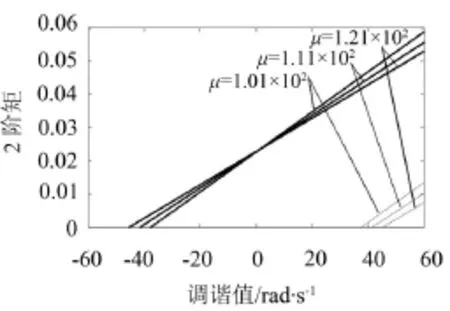
图5 不同μ值情况下均方响应曲线

5 主参数共振时间历程分析

根据4阶龙格-库塔法用编写程序得到系统表达式（3）的时间历程曲线和相图。

图6为V=0时系统的时间历程图，由图可知，随着时间的增加，振动的最大位移逐渐趋于稳定。图7为V=0时系统的相图。

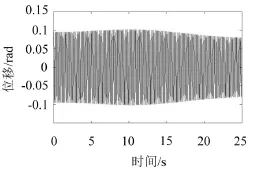
图6 V=0时的历程

图8和图9为V=0.01、V=0.1时系统主参数共振的时间响应曲线，对比图8和图9，可见得当V增大时柴油机轴系扭振系统的时间响应曲线变化不大。

图10和图11为V=0.01、V=0.1时系统主参数共振的相图。对比图10和图11可得当V增大时柴油机轴系扭振系统的相图极限环的厚度变化不大。

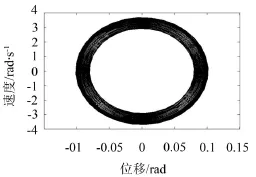
图7 V=0时的相图

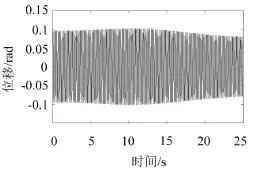
图8 V=0.01时的时间历程

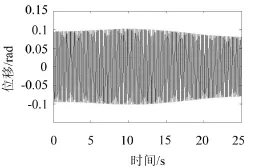
图9 V=0.1时的时间历程

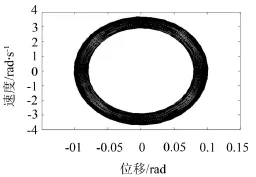
图10 V=0.01时的相图

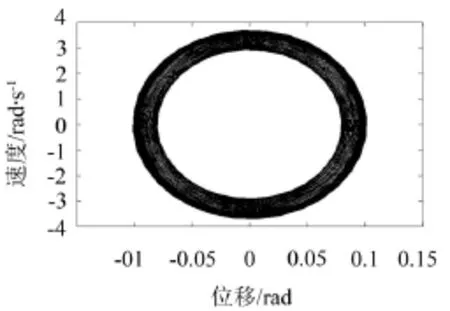
图11 V=0.1时的相图

6 结语

根据拉格朗日函数建立柴油机轴系扭振系统的动力学方程。应用改进多尺度法得到在有界窄带随机激励下柴油机轴系扭振强非线性系统的响应，得到主参数共振的幅频响应方程和系统均方响应的近似表达式，考虑了随机项对响应的影响。理论分析与数值计算表明改变柴油机轴系扭振系统的参数，响应的均方值也随之改变。结果表明，随着阻尼值的增大，系统主参数共振振幅的均方值减小；随着曲轴扭转刚度的减小，系统主参数共振的均方响应曲线的斜率增大；随着随机扰动强度的增大，系统时间响应曲线和相图变化不大；主参数共振稳态解稳定的充分必要条件与二阶矩稳定的充分必要条件是一样的。

[1]赵旭东.船用低速柴油机轴系扭振及其冰区特性的研究[D].大连：大连海事大学，2015.

[2]曾志龙.船舶轴系扭振应力测试技术研究[D].北京：中国舰船研究院，2014.

[3]杨志安，程欣桐.船用柴油机水冲击动力作用轴系的主参数共振[J].工程力学，2013，30：333-337.

[4]杨志安，程欣桐.船用柴油机膨胀气体冲击力作用轴系的主参数共振[J].工程力学，2010，27(7)：221-225.

[5]戎海武，王向东，孟光，等.窄带随机噪声作用下非线性系统的响应[J].应用数学和力学，2003，24(7)：723-729.

[6]杨志安，李熙，孟佳佳.改进多尺度法求解环形极板机电耦合强非线性系统主共振的研究[J].振动与冲击，2015，34(9)：208-212.

[7]PASRICHA M S.Effect of damping on parametrically excited torsionalvibrationsofreciprocating engines including gas forces[J].Journal of Ship Resarch,2006, 50(2):147-150.

[8]肖能齐，周瑞平，林晞晨.含非线性部件的船舶推进轴系自由振动解析[J].噪声与振动控制，2016，36(2)：135-138.

[9]程欧，苟向锋.多自由度齿轮系统非线性动力学分析[J].噪声与振动控制，2015，35(6)：31-35.

[10]程欣桐.考虑蒸汽力作用船舶柴油机轴系非线性振动研究[D].唐山：河北理工大学，2009.

[11]RONG HAI WU,XU WEI,FANG TONG.Principal Response of Duffing Oscillator to Combined Deterministic and Narrow-Band Random Parametric Excitation[J].Journal of Sound and Vibration,1998,210 (4):483-515.

[12]RONG HAI WU,MENG GUANG,FANG TONG.On the almost-sure asymptotic stability of second-order linear stochastic system[J].Journal Sound and Vibration, 2000,229(3):491-503.

[13]ZHU W Q.Stochastic jump and bifurcation of a duffing oscillatorundernarrow-bandexcitation[J].ActaMechanica Sinica,1994,01:73-81.

[14]朱位秋.随机振动[M].北京：科学出版社，1992.

Primary Parametric Resonance of Shafting Torsional Vibration System of the Diesel Engine Subjected to Narrow-band Random Excitation

YANG Zhi-an1,BIAN Ya-yuan2
(1.Key Laboratory of Structure and Vibration Engineering of Tangshan,Tangshan College, Tangshan 063000,Hebai China; 2.College of Mechanical Engineering,North China University of Technology, Tangshan 063000,Hebai China)

The primary parameters resonance and stability problems of strong nonlinear torsional vibration of the diesel engine shafting system under narrow-band excitation are investigated.The frequency response equation of the system is obtained based on the modified multi-scale method and the corresponding Ito stochastic differential equation is derived.By means of the moment method,the approximate expression of the mean-square response of the system is obtained and the influence of the system parameters on the mean square value of the primary parametric resonance is analyzed.The results show that the sufficient and necessary conditions for the stability of primary parametric resonance are the same as those of the second order moment stability.With the increase of the damping,the mean square value of the resonant amplitude of the primary parameters of the system decreases;With the decrease of the torsional stiffness of the crankshaft,the slope of the mean square response curve of the system increases;Along with the increase of the random disturbance intensity,the time response curve and the phase diagram of the system only have small changes.

vibration and wave;shaftin torsional vibration system of diesel engineg;narrow-band random excitation; modified multi-scale method;primary parametric resonance;mean square response

0324

：ADOI编码：10.3969/j.issn.1006-1335.2016.06.015

1006-1355(2016)06-0077-05

2016-05-05

河北省自然科学基金项目（A200900097）

杨志安（1963-），男，河北省秦皇岛市人，博士，教授，硕士生导师，研究方向为机构学与机械动力学。E-mail:yangzhi_an@163.com

卞雅媛（1989-），女，河北省廊坊市人，硕士研究生，研究方向为机构学与机械动力学。E-mail:1198606508@qq.com