非平面运动球式自动平衡装置数值仿真与实验

江 波，谭 青，罗 建

（中南大学 机电工程学院，长沙 410083）

非平面运动球式自动平衡装置数值仿真与实验

江 波，谭 青，罗 建

（中南大学 机电工程学院，长沙 410083）

实际生产过程中，高速转子由于受不平衡力矩作用，会产生非平面运动。通过数值仿真和实验，研究非平面运动球式自动平衡装置过临界转速下的运动特性。运用病态性探测实现数值仿真过程中刚性方法(ω方法)与非刚性方法(RK-45法)的自动切换。从而解决非平面运动球式自动平衡装置病态微分方程组的数值仿真与计算问题。通过对球式自动平衡实验台的实验研究验证了数值仿真与数学模型的正确性，并得出球式自动平衡装置对做非平面运动的转子的平面振动和空间转动都有很好的抑制作用和减振效果的结论。数值仿真算法在多体问题中具有借鉴意义。

振动与波；非平面运动；球式自动平衡装置；病态性探测

回转机械的平衡问题一直是机械行业的重要课题。尤其对于高速回转机械而言，转子由于质量分布不均匀而产生不平衡力与力矩会使回转机械产生振动和噪声，严重的甚至会引发灾难性破坏，由此造成的损失不容忽视。为了解决这一问题一般对转子采取高精度的动静平衡的方法[1]。但对于一些质量分布可能发生变化的回转机械如风机，经常将其卸载下来进行动静平衡很不方便。因此，近年来，对采用自动平衡装置来实现平衡、减振的研究引起了重视。这一技术对消除随机性不平衡尤为有效。自动平衡装置分为两种类型：一种是自动定心型的自动平衡装置，也称为被动式自动平衡装置[2]；另外一种是由微机控制的自动平衡装置，也称为主动式自动平衡装置[3-4]。球式自动平衡装置是一种性能优异的被动式自动平衡装置。

国内外对非平面运动球式自动平衡装置的系统性研究较少。以往对被动式自动平衡转置的研究主要集中在转盘平面不变的情况，从而忽略了由不平衡力矩引起的非平面运动。文献[5]完成了对非平面运动球式自动平衡装置的建模与稳定性讨论。考察文献[5]中的非平面运动球式自动平衡装置的数学模型，发现其雅克比矩阵条件数比较大，属于病态问题的初值问题。设计一种高效率、高精度的算法进行模型的数值仿真并最终通过实验验证仿真结果的可靠性和数学模型的正确性，对探索非平面运动球式自动平衡装置的运动特性具有重要的意义。

1 数学模型简要说明

实际应用过程中，高速运动的转子由于受到不平衡力矩的作用，会使整个转轴产生空间转动，这种转动使得转子产生非平面运动，从而使整个系统产生非平面运动。

非平面运动球式自动平衡装置的力学模型如图1所示。

图1 力学模型示意图

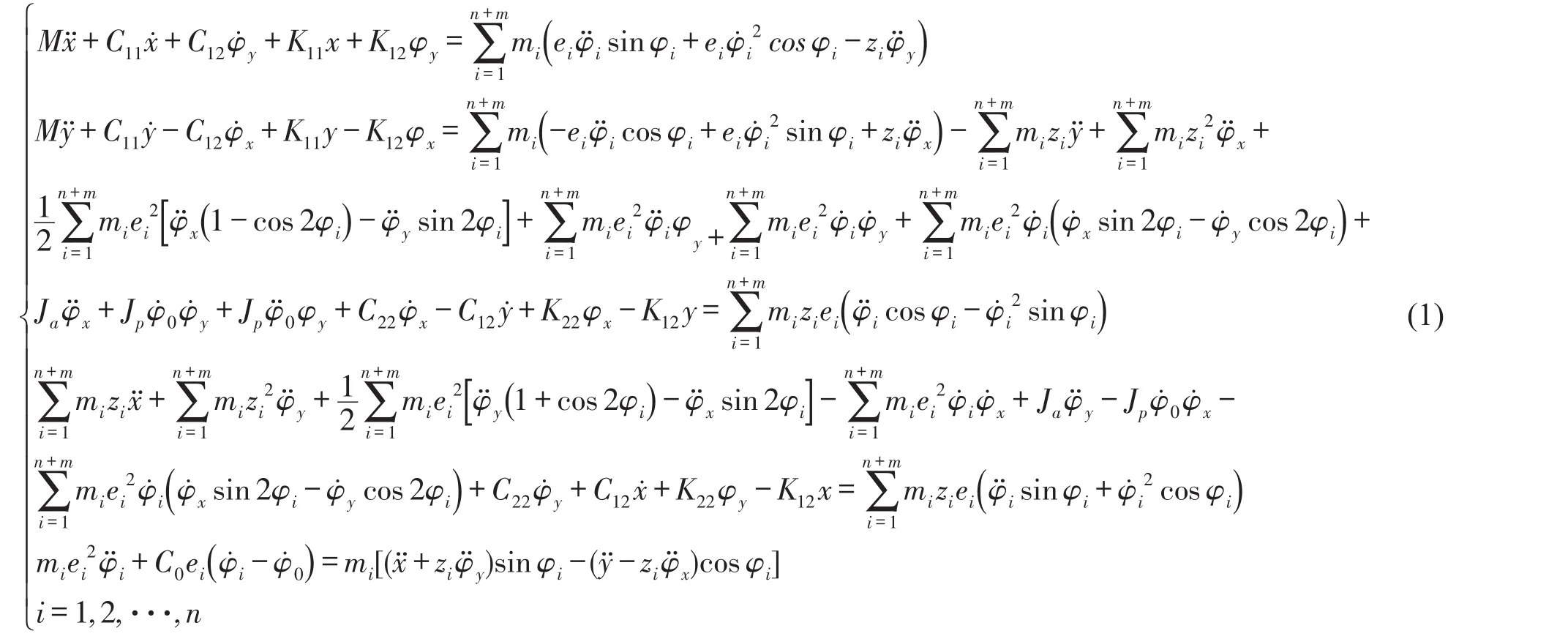
转盘上放置了n个滚球，作可移动的补偿量，同时在转盘上安放了m个偏心质量。

为了更清晰表达系统的非平面运动，尤其是转轴绕X、Y轴的转动行为，做出如图2所示的系统平面和空间振动示意图。

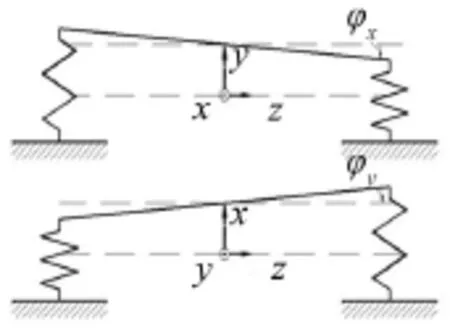
图2 平面和空间振动示意图

由文献[5]可知，非平面球式自动平衡装置的运动方程如式(1)所示。

式中主要采用的符号说明如下：

O0-XYZ：静止时的坐标系，O0为转轴中心静止时的位置；

O1-xyz：随转轴中心运动的坐标系，其中x-y平面始终与转盘平面平行，O1是转轴中心运动时的位置；

x、y：转轴中心由O0到O1的位移，单位为m；

φx、φy：转轴空间转动的角位移，单位为rad；

zi为第i个质点与系统质心之间的轴向距离，单位为m；ei第i个质点与回转轴线之间的距离即偏心距，单位为m，φi为第i个质点的转角，单位为rad（；其中i=1，···，n，n+1，···，n+m，前n个质点为滚球，后m个质点为偏心质量）；

M为系统的总质量，m为转盘转轴的质量，mi为第i个质点质量，单位为kg（其中）；

C、K为系统的阻尼矩阵、刚度矩阵，阻尼的单位为N·s/m，刚度的单位为N/m；

JRi、J分别为质点绕定轴转动的转动惯量矩阵、转轴与转盘的主转动惯量矩阵，转动惯量的单位为kg·m2；

φ0为转轴和转盘的转速，单位为rad/s；

C0为滚球黏性阻尼系数，单位为N·s/m·rad。

2 系统的数值仿真

2.1 病态问题及病态性探测

在很多重要的科学技术领域和实际问题中，往往会碰到这样一类系统，系统中有的状态变量因具有较小时间常数，变化速度较快，而有的状态变量因其具有较大的时间常数，变化速度相对缓慢，这就是所谓的病态问题[6]。通过Matlab可求出非平面运动球式自动平衡装置的Jacobi矩阵，依照Shampine和Gear给出的刚性初值问题的定义[7]，可发现非平面运动球式自动平衡装置的系统在某些区间内表现出病态性而在其他区间表现出非病态性。

关于非线性病态（刚性）初值问题的求解，国内外相关学者做过一些研究，主要采用Gear法、BDF法、α方法等具有较大稳定域甚至恒稳定的刚性方法解决，但此类方法通常要计算系统的Jacobi矩阵[8]。非平面运动球式自动平衡装置的数学模型的雅克比矩阵含有大量分式，求解雅克比矩阵将费时费力。当系统表现出严重病态性时，就要求计算步长特别小才能满足稳定性和精度要求。过小的步长势必导致需要同刚性比等量级的积分次数，即需要很大的计算量，进而导致仿真时间很长，甚至由于舍入误差的累积导致仿真失败[7]。在不表现出病态性时使用非刚性方法，在出现病态性时使用刚性方法，可以有效提高计算效率和精度。

病态性探测常用三种方法：稳定半径法、小稳定域试探法、嵌入低阶大稳定域法。考虑到非平面球式自动平衡装置的Jacobi矩阵比较复杂，求解耗时较多，因此采用嵌入低阶大稳定域法[6]。

2.2ω方法与RK-45法

非平面运动球式自动平衡装置的Jacobi矩阵比较复杂，计算困难，而ω方法是采用任意的实方阵代替精确的Jacobi矩阵，并通过改变步长的方式使该方阵具有良好的稳定性，故采用ω方法可以避免求解Jacobi矩阵的麻烦。ω方法的递推公式和误差估计可以参考文献[10]。

RKF-45法简写为R-45法，被公认是解决非刚性问题的最有效方法之一。Shampine提出RK-45中嵌入大稳定域1(2)阶的计算公式，其计算公式的形式与RK-45方法一致，只是误差估计系数上有区别。该方法的公式及公式中的系数可参考文献[6、11]。

2.3 模型降阶与数值仿真流程

在用数值计算方法求解常微分方程组时，通常都需要将高阶方程降阶为低阶方程，因此将2阶方程组式(1)降阶为1阶方程组是有必要的。受限于文章篇幅，现以系统存在两个球和一个偏心质量为例进行说明。

设：

当系统处于稳定状态时，转子转速恒定，滚球也将处于相对转盘静止的状态。假设盘以恒定转速运行，即为常量，且将式(2)代入式(1)就可以得到系统在稳态下的1阶形式的微分方程组见式(3)。

在迭代计算的过程中，利用病态性检测，结合病态判据，在ω方法与RK-45法之间根据方程当前是否处于病态进行自动切换，不用通过求复杂的雅克比矩阵判断当前步是否为病态，从而提高计算精度和效率。数值计算仿真程序是基于Matlab编写的，能够自动切换算法。具体的计算流程如图3所示。

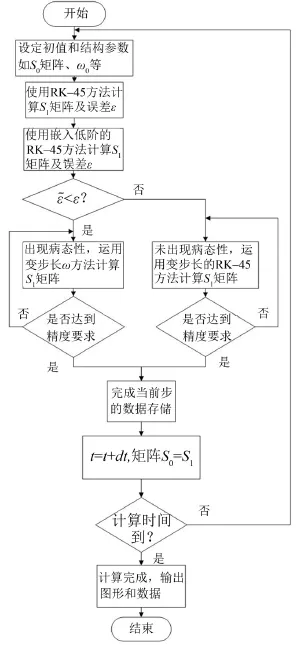
图3 仿真流程图

2.4 数值仿真结果

通过测量和实验发现，系统相比较于仅仅考虑平面运动的自动平衡装置系统出现了2阶固有频率。在系统参数如表1所示的情况下通过测量得到系统两阶固有频率，分别为

ωn1≈10.7 πrad/s，ωn2≈47.7 πrad/s。

表1 仿真与实验参数

主要探讨非平面球式自动平衡装置在过临界转速下的动态特性和减振效果，设定仿真的初始条件为：S0=(0，0，0，0，0，0，0，0，2π/3，0，-2π/3，0)T，其他的结构参数值如表1所示。为了研究自动平衡装置在过1阶临界转速、过2阶临界转速时的性态和减振效果，取转速ω1=30 πrad/s，ω2=90 πrad/s，分别以无球和两个球进行仿真，得出如表2和图4所示的仿真结果。

表2 仿真结果汇总表

由仿真结果可知，系统存在两阶固有频率，因此球式自动平衡装置运用在作非平面运动的旋转机械上面时必须考虑系统的1阶和2阶固有频率。

对比表2中无球时过1、2阶临界转速的振幅情况可知，工作转速为过1阶临界转速时的平面振动较大，而空间振动相对较小；而当转速过度到过2阶临界转速时，空间振动增加较大，而平面振动变化并不明显。这说明非平面运动球式自动平衡装置的1阶固有频率主要产生于平面运动，而2阶固有频率主要产生于空间转动。对比表2中无球和有球时的振动幅值可知，在过1阶临界转速时，有球时平面振幅和空间振幅的幅值分别约为无球时的1/15和1/ 16；在过2阶临界转速时，有球时平面振幅和空间振幅的幅值分别约为无球时的1/9和1/24。过临界转速时球式自动平衡装置对转子有很好的减振效果，尤其在过2阶临界转速时减振效果更为显著。图4 (a)至(d)显示，在过2阶临界转速时球式自动平衡装置对平面振动和非平面振动（空间振动）都有很明显的削减作用。图4(e)和(f)显示，工作转速为过2阶临界转速时，由于其能更快速通过两个共振区，因此与工作转速为过1阶临界转速时的情况相比，滚球稳定下来所花费的时间更少，平衡所需时间更少（过1阶临界转速平衡时间为1 s而过2阶临界转速平衡时间大约为5 s）。

综上所述，球式自动平衡装置在亚临界转速下对系统减振不利，在过1阶临界转速时有很好的减振效果，在过2阶临界转速时减振效果较过1阶临界转速效果更好。

3 实验验证

设计了图5和图6所示的实验方案和试验台。

变频器可以控制实验台的电机转速；压电式加速度传感器将所采集到的实验台振动信号输送到电荷放大器中进行放大；数据采集卡将放大后的加速度电压信号转换成数字信号（即进行A/D转换）输送到计算机中进行处理和计算。

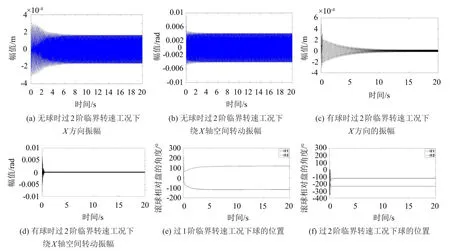
图4 仿真结果示意图

图5 实验整体方案

图6 实验平台

在与仿真系统参数和条件相同的情况下进行实验，通过数据采集卡和计算机进行数据采集，得到如表3和图4所示的实验结果。因为主要着眼于研究减振效果，故只给出稳态时的实验数据。

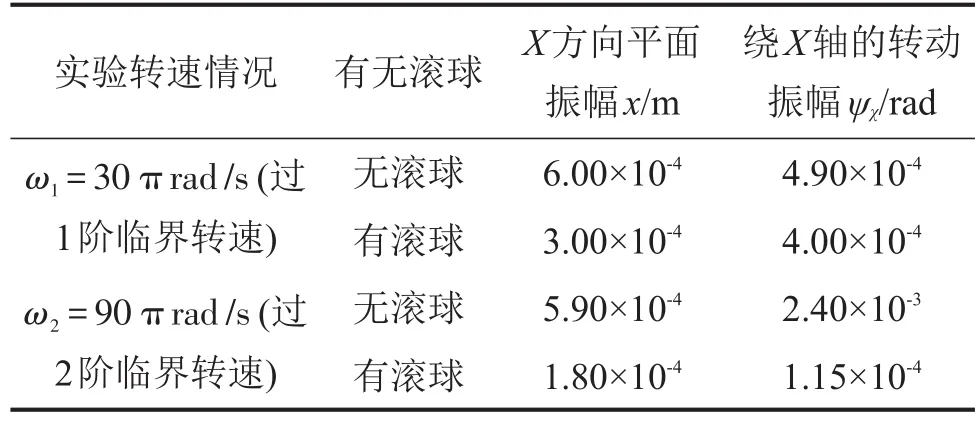
表3 实验结果汇总表

对比表3中无球和有球时的振动幅值，可知在过1阶临界转速工况下，有球时平面振幅和空间振幅的幅值分别约为无球时的1/2和4/5；在过2阶临界转速工况下，有球时平面振幅和空间振幅的幅值分别约为无球时的1/3和1/21。通过对比发现仿真结果与实验结果在减振趋势上具有一致性，在过临界转速工况下，装有球式自动平衡装置的回转机械比没有球式自动平衡装置的振幅小很多。对比表3中的数据可知，无球时工作转速为过1阶临界转速工况下的平面振动较大，空间振动相对较小；而当工作转速过2阶临界转速时，空间振动增加较大，平面振动变化并不明显。当有球时，在过临界转速工况下系统的平面振幅和空间振幅相对于无球时都呈削减趋势。实验表明在过临界转速下球式自动平衡装置对平面振动和空间振动都有很好的抑制作用，在过2阶临界转速工况下对平面振动和空间振动的削减作用更明显。这与仿真得到的结论一致，说明了数学模型和仿真的准确性。

由于加速度计存在横向效应，采集平面运动信号的加速度传感器所采集到的振动信号并不完全是平面运动的信号而是平面运动与少量空间运动信号的叠加，振幅是通过对加速度信号两次积分得到的，有积分误差，同时实际工程中转盘并不是完全均匀对称的，所以实验与仿真相比具有一定误差。而且，由于是微小振动，振幅相对较小，误差的影响也相对较大。但实验结果中表现出的减振趋势与仿真显示的减振趋势具有一致性。

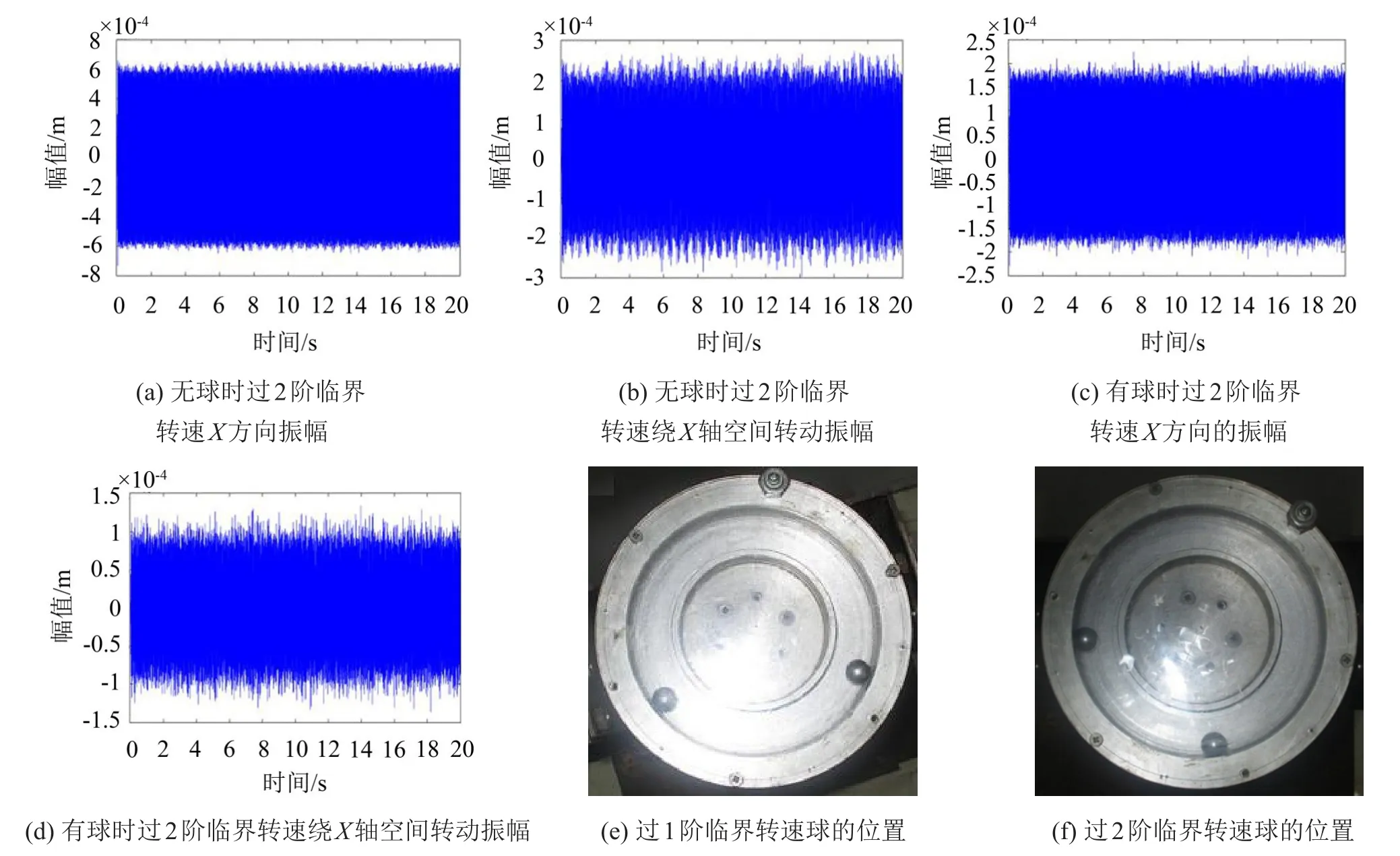
图8 实验结果示意图

4 结语

球式自动平衡装置对受不平衡力矩的回转机械具有很好的减振效果，当偏心量较大时将尤为明显。在过1阶临界转速和过2阶临界转速工况下都具有较好的减振效果，并且在过2阶临界转速工况下的减振效果要好于过1阶临界转速，因为过2阶临界转速后球的位置分布使系统质心更靠近回转中心。

无球时，工作转速为过1阶临界转速时平面振动明显，而空间振动并不很明显，而当工作转速过度到过2阶临界转速时，空间振动明显增加，而平面振动变化并不明显。这说明非平面运动球式自动平衡装置的一阶固有频率主要产生于平面运动，而2阶固有频率主要产生于空间转动。

实验结果显示的球式自动平衡装置对受不平衡力矩作用的高速转子在过临界转速工况下的减振趋势和动态特性与仿真结果相一致，说明文献[5]所给出的非平面运动球式自动平衡装置数学模型的正确性和文中所用数值仿真方法的可行性。文中所述的数值仿真方法对多体动力学数值仿真具有一定借鉴意义。

[1]刘文倩，谭青，谢燕琴，等.自动平衡装置减振效益分析[J].噪声与振动控制，2010，30(4)：153-157.

[2]谭青，周铁，黄秀祥.球式自动衡装置的数值仿真与实验研究[J].噪声与振动控制，2008，28(3)：142-145.

[3]曾 胜，汪希萱.电磁式在线自动平衡调节器的原理及其实验[J].流体机械，1997，25(5)：11-14.

[4]陶利民，葛哲学，温熙森.刚性转子自动平衡控制策略[J].机械科学与技术，2004，23(3)：142-145.

[5]罗建，谭青，江波.非平面运动球式自动平衡装置稳定性分析[J].噪声与振动控制，2016，36(2)：21-26.

[6]肖田元.系统仿真导论[M].北京：清华出版社，2010：74-111.

[7]李寿佛.刚性常微分方程及刚性泛函微分方程数值分析[M].湖南湘潭：湘潭大学出版社，2010：22-31.

[8]熊光楞，宋安澜.数字仿真中的病态探测和积分方法的自动切换[J].信息与控制，1985，(2)：12-18+63.

[9]RODRIGUES D J,CHAMPNEYS A R,FRISWELL M I, etal.Experimentalinvestigation ofa single-plane automatic balancing mechanism for a rigid rotor[J].Journal of Sound and Vibration,2011,330(3):385-403.

[10]朱因远，周纪卿.非线性振动和运动稳定性[M].西安：西安交通大学出版社，1992：218-221.

[11]SHAMPINE L F,HIEBERT K L.Detecting stiffness with the Fehlberg (4,5) formulas[J].Computerand Mathematics withApplications,1977,3(1):41-46.

Numerical Simulation and Experimental Research of Ball-type Automatic Balancer Devices with Non-plane Motion

JIANG Bo,TAN Qing,LUO Jian
（School of Mechanical and Electrical Engineering,Central South University,Changsha 410083,China）

In practical production,high speed rotors will produce the non-plane motion due to unbalance torques.In this paper,through numerical simulation and experiment,kinematic characteristics of non-plane ball type automatic balancing devices under the critical speed are studied.Using the ill-conditioned detection method,automatic switching between the stiff method(ω method)and the non-stiff method(RK-45 method)in the numerical simulation is realized.The corresponding ill-conditioned differential equations of the ball-type automatic balance device with non-plane motion are solved.The correctness of the mathematical model and numerical simulation results is verified through experiments.It is concluded that the ball-type automatic balance device has a good damping effect for the planar vibration and spatial rotation of the rotors with non-plane motion.The numerical simulation algorithm has reference significance for multi-body problem analysis.

vibration and wave;non-plane motion;ball-type automatic balance device;ill-conditioned detection

TH113.1

：A

：10.3969/j.issn.1006-1335.2016.06.011

1006-1355(2016)06-0056-06

2016-06-20

江波(1991-)，男，湖南省永州市人，硕士研究生，主要研究方向为机械振动控制。E-mail:jiangbo_csu@163.com