层次分析法的改进及其在权重确定中的应用

张 乐 曹 爽 李士雪 徐凌忠 李群伟

层次分析法的改进及其在权重确定中的应用

张 乐1曹 爽2李士雪3徐凌忠3李群伟1

权重的确定对于评价或测量具有十分重要的意义，关系着评价或测量结果的可靠性，目前确定权重的方法较多，其中层次分析法较为常用。层次分析法由美国学者T.L.Saaty于1970年创建，目前在公共决策领域发挥了重大的作用［1-2］，但许多学者［3-4］对其提出了质疑，他们认为层次分析法并没有改变以往基于“基数”赋权的本质，即“阿罗困境”，而合理的赋权方法应该是基于“序数”的［5-6］，本研究为了摆脱以往指标赋权的“阿罗困境”，以职业病防治绩效评价指标的权重确定为例，对层次分析法确定权重的算法进行改进。

方法的改进与步骤

本研究利用改进的层次分析法，基于“序数”赋权。基本步骤叙述如下：

1.专家咨询

邀请相关领域的专家对各指标之间进行两两比较，专家按照的方向，若专家认为指标Im比In重要则在相应表格中填“+”号，若认为二者同等重要，则填“＝”号，若认为Im不如In重要则填“-”号。在填写过程中必须遵循“传递性”原则：如果指标Im比Ik重要，同时Ik比In重要，则Im比In重要，反之亦然。

2.统计专家咨询的结果

对专家咨询的结果进行统计汇总，认为指标Im比In重要的专家所占的百分比，记为P；认为二者同等重要的专家所占的比例，记为E；认为指标Im不如In重要的专家所占的百分比，记为M，显然P+E+M＝1。

3.建立映射

根据统计汇总的资料，以（P-M）的值作为建立映射的标准，详见表1。若（P-M）为负值，则对其按照1／9～1进行相应赋值。

表1 基于P-M值的映射规则

下面步骤与传统的层次法一致：（1）根据专家咨询的统计结果以及所建立的映射标准，建立各层次指标的判断矩阵；（2）计算权重系数；（3）对判断矩阵进行一致性检验；（4）计算判断矩阵的随机一致性比率。

计算实例

本研究以职业病防治绩效评价为实例，来说明改进的层次分析法的具体计算过程。职业病防治绩效评价指标体系包括投入、产出和结果三个维度，投入维度又包括有形投入和无形投入两个指标，产出维度包括服务提供、依法行政和行业自律三个指标，结果维度包括健康促进和社会影响两个指标。

1.专家咨询及映射

本研究共邀请27名在相关领域工作十年以上的专家，对职业病防治绩效评价指标，进行两两重要性比较。专家的研究领域涵盖了卫生管理、职业卫生、流行病学和临床医学等专业，工作单位涉及行政管理、公共卫生机构以及教育与科研机构。具体咨询结果详见表2。

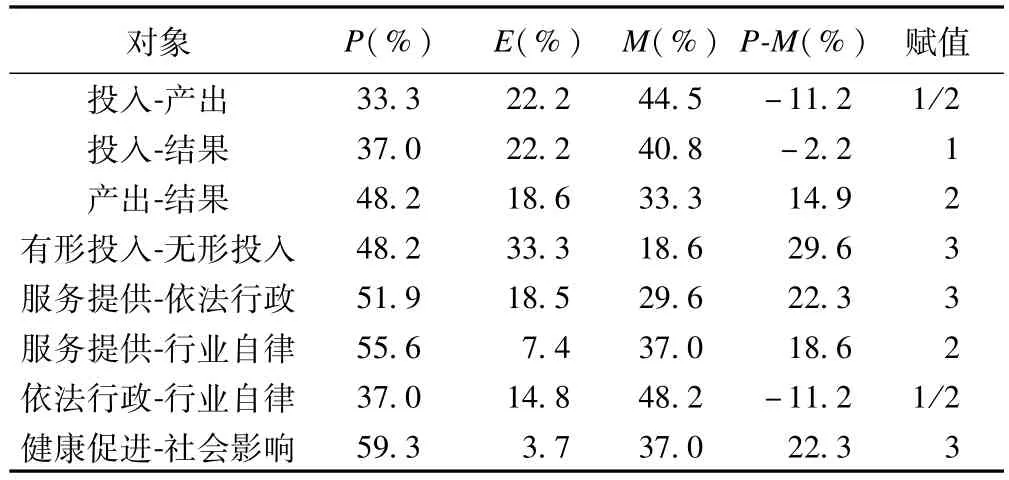
表2 层次分析法专家咨询统计结果

2.权重确定及一致性检验

根据专家咨询及映射结果，可以建立各层次指标的判断矩阵，从而计算出各指标的权重，并进行相应的一致性检验。

（1）一级指标权重确定及一致性检验

一级指标投入、产出及结果的权重分别为0.250、0.500和0.250，一致性检验结果显示，λmax＝3.0000，CI＝0.0000，CR＝0.0000＜0.1，详见表3。

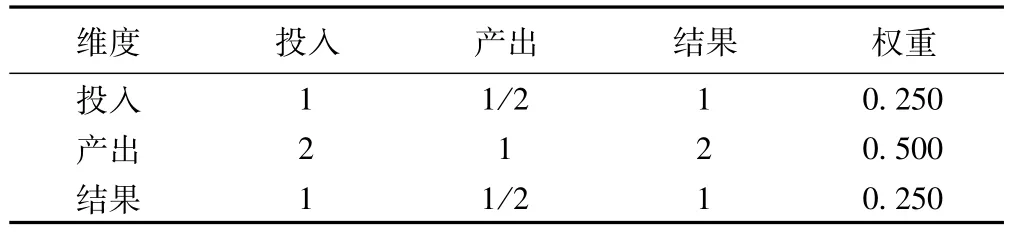
表3 一级指标权重及一致性检验

（2）二级指标权重确定及一致性检验

投入维度有形投入和无形投入的权重分别为0.750和0.250，详见表4。

表4 投入维度指标权重及一致性检验

产出维度服务提供、依法行政和行业自律的权重分别为0.540、0.163、0.297，一致性检验结果显示，λmax＝3.0092，CI＝0.0046，CR＝0.0080＜0.1，详见表5。

表5 产出维度指标权重及一致性检验

结果维度健康促进和社会影响的权重分别为0.750和0.250，详见表6。

表6 结果维度指标权重及一致性检验

同时，虽然各层次均已经过层次单排序的一致性检验，各成对比较判断矩阵具有较为满意的一致性，但是当综合考察时，各层次的非一致性仍然有可能积累起来，引起最终分析结果的较为严重的非一致性，本文又对总一致性进行了检验，CR＝0.011＜0.1，故改进后的层次分析法总排序的一致性较为理想。

3.职业病防治绩效评价实证研究

本研究按照经济实力以及工业化水平，从山东省选择烟台市、威海市、莱芜、济南市、潍坊市、济宁市、聊城市、枣庄市和菏泽市等九个市，利用构建的职业病防治绩效评价指标体系，采用综合指数法对其进行评价，评价结果详见表7。

表7 样本地区职业病防治绩效评价结果排序

按照改进的层次法确定各指标权重，与按照普通的层次分析法确定的权重相比，虽然绩效指数有较大改变，但样本地区职业病防治绩效评价结果排序基本没有变化，只有威海市和济宁市的排序发生转换，这主要是因为这两个样本市绩效指数很接近。

讨 论

本研究在使用层次分析法确定指标权重时，对其进行了相应的改进。以往在使用层次分析法赋权时，往往需要专家对指标的相对重要性按照1～9的标度进行赋值，而在实际操作中专家往往很难把握各个分值之间的差异，因此赋值具有很大的主观性和不确定性［7］。

同时，由于层次分析法按照1～9的标度进行赋值，其本质仍然是基于“基数”赋权，难以摆脱“阿罗困境”，而本研究则是基于“序数”赋权，能够解决这一难题。改进的层次分析法简单易行、便于操作，而且确定的权重结果也是可靠的，主要表现在两点，首先，一级指标和二级指标均可以通过一致性检验，其次，改进的层次分析法与普通的层次分析法相比，对样本地区职业病防治绩效评价结果的排序基本无影响。

当然，改进的层次分析法仍然有其不足之处，但毕竟提供了一个建设性的思路，同时，与常规的层次分析法一样，改进的层次分析法也存在主观性太强的问题，因此，本研究在确定职业病防治绩效评价指标权重时，同时采用熵值法与之相结合进行组合赋权，这里不再赘述。

［1］夏萍，汪凯，李宁秀.层次分析法中求权重的一种改进.中国卫生统计，2011，28（2）：151-157.

［2］黄宝宏.层次分析法在评价应用中的统计学审视.中国卫生统计，2008，25（2）：201-204.

［3］袁政.政府绩效评估权重设计中AHP法之改进.统计研究，2008，25（7）：39-44.

［4］蔡立辉.政府绩效评估.北京：中国人民大学出版社，2012.

［5］肯尼斯.阿罗.社会选择：个性与多准则.北京：首都贸易大学出版社，2000.

［6］刘颖芬，占济舟.比例标度一致性比较的新方法.统计与决策，2007，8.

［7］张乐.职业病防治绩效评价及分析研究.山东大学，2014.

1.泰山医学院公共卫生学院（271016）

2.济南市儿童医院

3.山东大学公共卫生学院

郭海强）