遗传算法在极端顶点混料设计的处方优化中的应用*

任 雯 刘春艳，2 赵 磊 王 祥 王华芳 魏 珍 仇丽霞△

遗传算法在极端顶点混料设计的处方优化中的应用*

任 雯1刘春艳1，2赵 磊1王 祥1王华芳1魏 珍1仇丽霞1△

目的 研究单目标遗传算法对极端顶点混料设计处方优化的效果。方法 选用自微乳化释药系统极端顶点混料设计的试验数据，采用全局优化的遗传算法进行混料配比优化，并与原文献中传统的等高线图法优化效果进行比较。结果 经单目标遗传算法优化后，自微乳化释药系统的三种成分：油相、表面活性剂、助表面活性剂所占比例分别为33.0%、10.0%、57.0%时，总黄酮类化合物的溶解度为49.12mg／g，比等高线法图求得的值增大1.32mg／g，增加了2.76%；微乳粒径大小为22.92nm，比等高线图法求得的值减小2.02nm，降低了8.10%。结论 遗传算法求解的最优解，达到了较好的效果，寻优过程中避免了传统方法存在的主观性和局部最优的缺陷，证明了单目标遗传算法在极端顶点混料设计的处方优化中具有实用价值。

遗传算法 极端顶点混料设计 单目标优化

混料设计是解决药物最优配方、配比最理想的一种试验设计方法，药物制剂的各混料组分所占比例的取值范围为［0，1］，且各组分总和为 1［1］，称其为定和约束。如果某一组分的上界或下界为一确定的比例约束，称为含上、下界约束的混料问题，如自微乳化释药系统中，表面活性剂的取值范围为［0，0.4］、助表面活性剂的取值范围为［0.3，1］，这类混料问题常采用极端顶点混料设计。

针对含上、下界约束的极端顶点混料设计的单目标优化问题，多数文献中采用的是传统的等高线图法。但这种方法只能解决决策变量在三维及以下的优化问题，对于决策变量维数较高的优化问题，求解过程复杂，寻得的最优解有时只是局部最优，且存在极大的主观性。鉴于等高线图法在应用中存在的不足，近年来提出了一种全局优化方法——遗传算法（genetic algorithm，GA），它是一种基于Darwin的进化论和Mendel的遗传学说的优化方法。已有研究表明：对于单目标优化，遗传算法不要求对优化问题的性质作深入的数学分析，在非连续性、多峰、噪声的情况下，搜索具有稳健性，以很大的概率收敛到最优解；搜索过程中不受优化函数连续性的约束，不要求优化函数导数必须存在；搜索效率高，可用于参数空间较大的优化问题；擅长全局搜索，可以有效地避免局部最优，为单目标优化提供全局最优解［2-3］。课题组已将遗传算法应用于中药有效成分最优提取条件的研究中，结果表明，方法可行、结果合理［4-6］。但遗传算法对于有定和约束的极端顶点混料配比的优化效果如何，尚未见报道。

本文旨在将单目标遗传算法应用到极端顶点混料设计的药物配比优化问题，利用 Genetic algorithm platforms v1.0软件在约束条件范围内完成遗传算法寻优，搜索出的最优解与原文献中等高线图法求得的结果进行比较，为极端顶点混料设计的处方优化研究提供更为科学、高效的方法。

原理与方法

1.极端顶点混料设计

在许多混料试验中，常常有些组分被限定在某一范围内，即不是在［0，1］范围内任意取值，而是受到上界或下界的约束的限制（式（1））。极端顶点设计是解决受上、下界约束混料问题的一种常用方法。

对于单形坐标系，同时满足式（1）中上下界约束条件的点的总体就是p维正单形内的一个p维凸多面体。所谓极端顶点设计，就是把试验点取在该凸多面体的顶点及各个（p-1）维边界面的重心上，或者再加上各顶点的重心所构成的混料试验设计。

2．模型的建立

由于定和约束，混料试验建模时不能采用一般的多项式作为回归模型，常采用称为Scheffe多项式的数学模型，常见的Scheffe多项式有二次式、完全三次式等形式：

二次式

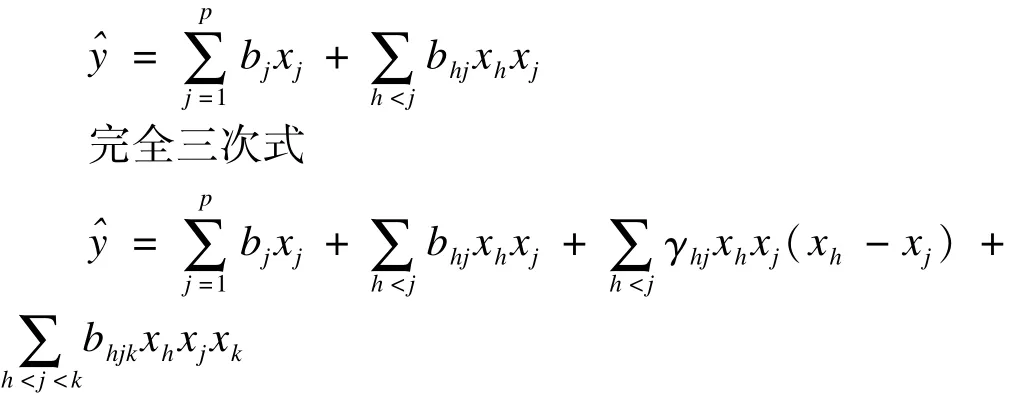
3.遗传算法

遗传算法具有广泛的适应性和很强的全局优化搜索能力；其基本思想是基于Darwin的进化论和Mendel的遗传学说，根据适者生存、优胜劣汰的自然法则，模拟进化过程中选择、交叉、变异的现象搜索最优解。在混料定和约束条件限制下的遗传算法的基本过程［4，7-8］为：①随机产生初始染色体（各组分的取值）种群，种群中染色体的数目称为种群大小，一般为30～100；②用Scheffe多项式作为目标函数评价每一染色体优劣；③以轮盘赌的方式选择评价值高的优良染色体作为新一代种群，评价值高的染色体被选择的机会多，而评价值低的染色体被选择的机会少；④交叉过程产生新型的基因，进而生成进化程度更高的群体；⑤变异过程，随机地对基因进行强制变化，其目的是改变搜索方向，扩大搜索空间，挖掘种群中个体的多样性，克服收敛于局部最优解的弊病。经过上述5个过程的运算产生的染色体称为后代，且每一步产生的新染色体均要满足混料定和约束的条件。在此基础上，继续对新的后代重复地进行评价、选择、交叉和变异操作，经过一定代数的进化后，就可以把最好的染色体作为优化问题的最优解。

实例分析

1.数据资料

在柿子叶提取物的自微乳化释药系统（SNEDDS）处方优化研究［9］中，柿叶提取物具有降压、治疗中风、抑制肿瘤等多方面的作用，研究表明，柿叶中的黄酮类化合物是其主要有效成分。但黄酮类化合物水溶性较差，致使其在常规制剂中的溶解和释放速率很慢，最终导致其在胃肠道内的吸收和利用程度很低。自微乳化释药系统作为一种新的药物载体，由油相、表面活性剂和助表面活性剂组成，药物被包裹在油滴中，口服后在胃肠蠕动下药物迅速地以微乳的形式释放，所形成微乳粒径分布在10～100nm。自微乳化释药系统能够提高难溶性药物的溶解度，进而提高药物的口服吸收度［10］，可用来解决柿叶提取物常规制剂生物利用率低的问题。

该SNEDDS释药系统的3个混料组分：油相（oil）、表面活性剂（surfactant）、助表面活性剂（co-surfactant）分别用 x1、x2、x3表示，取值范围见表1。由于各混料成分有上、下界的约束，采用Minitab15.0软件进行极端顶点设计，16个混料配比方案见表2。释药系统的评价指标为SNEDDS中黄酮类化合物的溶解度（y1）和用蒸馏水稀释后所形成的微乳粒径的大小（y2），其结果见表2。该混料处方优化的目的是：确定黄酮类化合物溶解度最大、微乳粒径最小的3个混料组分的最优配比。其中，溶解度（y1）可接受的范围18～54mg／g，微乳粒径（y2）可接受的范围 17.5～202.5nm。

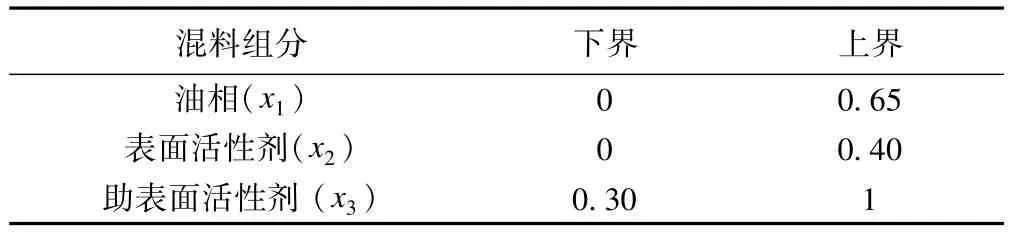
表1 混料组分的取值范围

2.目标转换

根据评价指标的可接受范围和目标，采用Derringer［11］提出的满意度函数法，将每个评价指标转换成使其最大化的中间变量d1、d2，再将其几何均值定义为满意度函数，使多目标问题转化为单目标问题，对满意度函数进行最大值优化。

要求溶解度y1达到最大，则中间变量定义为

要求微乳粒径y2达到最小，则中间变量定义为

定义满意度函数（D）如下：

其中k为评价指标的个数，满意度函数值越接近1越理想。求得的满意度函数值见表2。

表2 SNEDDS极端顶点混料设计方案及试验结果

3.模型建立方法

在混料约束条件下建立满意度函数（D）与3个混料组分的回归模型，按α＝0.05水准，在SAS9.2软件中构建出有统计学意义的Scheffe完全三次多项式回归模型。

最终构建出的模型F＝16.09，P＝0.0015，模型拟合较好。模型及决定系数（R2）如下：

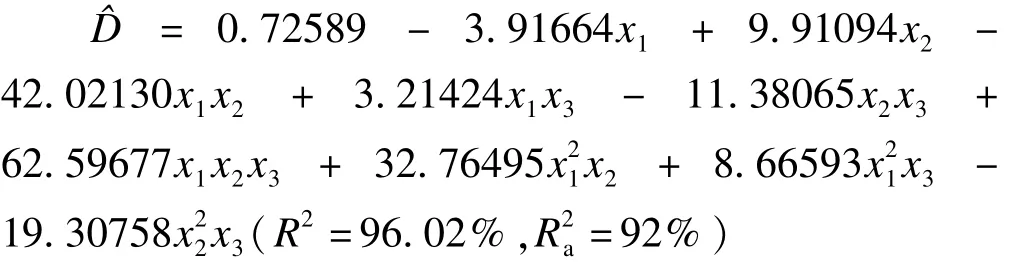
4.遗传算法优化结果

以构建出的满意度函数（D）的回归模型为目标评价函数，利用北京师范大学系统科学系系统分析与综合实验室开发的Genetic algorithm platforms v1.0软件对其进行优化，初始种群设为60，单点交叉概率设为0.9，变异概率设为0.03，最大进化代数设为200，在混料定和约束条件下进行50次随机搜索。

遗传算法优化的满意度函数进化图见图1。从图中可以看出，在混料约束条件以及各组分的上下界约束条件下，大约在进化到30代时，目标函数值达到最大，且搜索结果趋于稳定，稳定在接近1的水平。

表3给出了遗传算法优化满意度函数50次的部分运行结果，从表中可以看出，在混料各约束条件范围内，目标函数的最大值达到接近1的水平，且目标函数的最优值较稳定、精确。在表3的进化解方案中，8、14、27、35、42方案的自微乳化释药系统的三种成分x1、x2、x3在混料中所占的比例分别为 0.330、0.100、0.570时，总体满意度函数值（D）达到最大，为0.9558。

图1 遗传算法优化的满意度函数值D的进化图

表3 遗传算法优化的满意度函数（D）的部分进化解方案

将表3遗传算法优化结果中各混料组分及满意度函数值整理得到表4。x1、x2、x3在混料中所占的比例平均为0.325、0.100、0.575，满意度函数值＾D平均水平为0.9500，变异度为0.0129，变异度较小，结果较稳定。

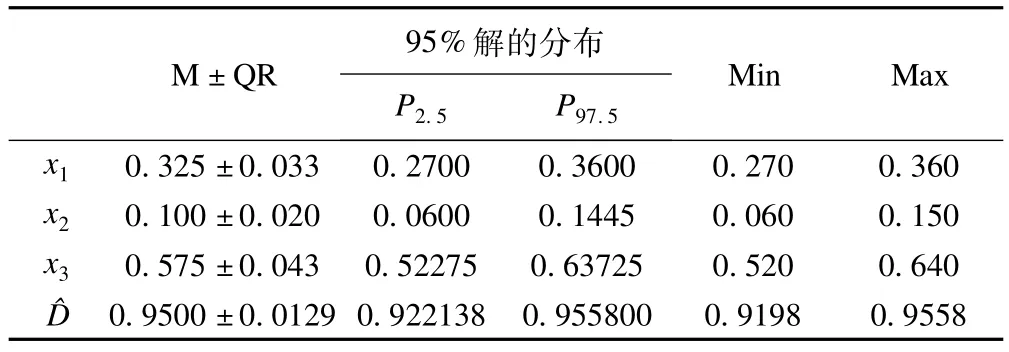
表4 遗传算法优化目标函数所得结果

5.优化效果比较

遗传算法求得的自微乳化释药系统的三种组分油相、表面活性剂、助表面活性剂在混料中所占的比例分别为33.0%、10.0%、57.0%时，评价指标满意度函数值＾D达到最大为0.9558，比等高线图法的最优值0.951增大了0.0048，增加了0.5%。溶解度（y1）和微乳粒径大小（y2）与三个混料组分的回归模型用Expert Design V8.0.6.1构建，模型如下：

将最优函数值对应的配方配比值带入到总黄酮类化合物的溶解度（y1）和微乳粒径大小（y2）的函数中，求解得到总黄酮类化合物的溶解度y1为49.12mg／g，比原文献中等高线图法求得的47.8mg／g增大了1.32mg／g，增加了 2.76%；微乳粒径大小的值为22.92nm，比等高线图法求得的24.94nm减小2.02nm，降低了8.10%，结果见表5。

表5 遗传算法与等高线图法求得的最优解的比较

讨 论

含上界或下界约束的混料问题常采用极端顶点混料设计，在解决这类设计的优化问题时，传统方法常采用等高线图法。等高线图法是通过绘制三维立体等高图，在最优范围内人为地选取最优解，具有极大的主观性，且不能提供精确的最优解。遗传算法作为一种新的寻优方法，整个搜索过程均在混料定和约束下进行，有效克服了等高线图法主观性太强的弊端，同时，遗传算法能够搜索出多个精确的可供选择的相应混料配方组合，实际应用中研究者可以根据需要选择合适的最佳配方配比。

如果在解决三个以上混料组分的优化问题时，由于目标函数的空间结构是超曲面的，问题的复杂性增高，不能画出等高线图，需进行降维处理，或者将某一组分控制在一个固定水平值上，通过其他组分绘制等高线图，这不是在所有组分空间结构上的整体优化，所以等高线图法的应用受到限制。而遗传算法可以弥补这一不足，它是一种全局优化方法，适合多变量、非线性优化，在混料组分较多的情况下表现出巨大的优越性，可以进一步推广到三个以上混料组分的处方优化研究。

［1］Eide I，Johnsen HG.Mixture design and multivariate analysis in mixture research.Environmental health perspectives，1998，106（Suppl）：1373-1376.

［2］戴帅，师先锋，王婷，等.孟德尔多目标简单遗传算法在药物提取条件优化中的应用.中国卫生统计，2014，31（4）：615-619.

［3］冯瑞梅，王婷，戴帅，等.中心复合设计最优条件选取时四种方法的比较.中国卫生统计，2014，31（3）：387-389.

［4］周建淞，张晓丽，韩荣荣，等.遗传算法在单目标混料均匀设计优化实例中的应用.中国药物与临床，2010，10（11）：1213-1216.

［5］吴小娟，刘春艳，王晓美，等.小生境遗传算法多目标优化金莲花的醇提工艺.中国药房，2014（3）：228-231.

［6］徐彦杰，刘晓红，杨晓文，等.向量评估遗传算法优化珍珠菜抗肿瘤有效成分的研究.中国卫生统计，2012，29（6）：815-818.

［7］仇丽霞.基于遗传算法的最优决策值选择及医药学应用研究.山西：山西医科大学，2007.

［8］仇丽霞，刘桂芬，何大卫，等.二次响应面回归模型用遗传算法探索最优试验条件.中国卫生统计，2004，21（4）：3-6.

［9］Li W，Yi S，Wang Z，et al.Self-nanoemulsifying drug delivery system of persimmon leaf extract：Optimization and bioavailability studies.Int J Pharm，2011，420（1）：161-171.

［10］毛厌草，谢新，黄秋霞.SMEDDS在中药制剂中的应用研究进展.中医药导报，2010，16（1）：88-90.

［11］Derringer GC，Suich R.Simultaneous Optimization of Several Response Variables.Quality Technology，1980，12：214-219.

The Application of Genetic Algorithm in the Formulation Optimization of Extreme Vertices Mixture Design

Ren Wen，Liu Chunyan，Zhao Lei，et al
（Shanxi Medical University（030001），Taiyuan）

Objective To study the application of single-objective genetic algorithm in the formulation optimization of extreme vertices mixture design.Methods The literature results designed by the extreme vertices mixture design will be optimized using the genetic algorithm to select the best formulation，which will be compared with ones optimized by the conventional methods of the original text.Results The formulation was optimized by single objective genetic.It was showed that when proportion of three components of oil，surfactant and co-surfactant derived from micro-emulsion delivery system was 33.0%，10.0%，57.0%，respectively，the total flavonoids solubility in the delivery system was 49.12mg／g more 1.32mg／g，which increased 2.76%than one using the contour diagram strategy and smaller droplet size reached 22.92nm lowering 1.32nm，which decreased 8.10%than the contour diagram value.Conclusion Formulation optimization based on genetic algorithm shows the good performance of the algorithm.In the process of optimization，it avoids some shortcomings of classical methods in the application such as a great deal of subjectivity and local optimum to some extent，so single-objective optimization might be used in the formulation optimization of extreme vertices mixture design.

Genetic algorithm；Extreme vertices mixture design；Single-objective optimization

*：山西省自然科学基金项目（2013011059-3）

1.山西医科大学公共卫生学院卫生统计学教研室（030001）

2.太原铁路局疾病预防控制所

△通信作者：仇丽霞，E-mail：qlx_1126＠163.com

刘 壮）