多种填补方法在纵向缺失数据中的比较研究

鲍晓蕾 高 辉 胡良平

多种填补方法在纵向缺失数据中的比较研究

鲍晓蕾1高 辉2胡良平3

目的 比较多种方法对纵向缺失数据的处理效果。方法 运用SAS软件通过蒙特卡罗模拟产生最常见的含一个分组因素和一个重复测量因素的纵向资料，对其进行混合效应模型分析，将结果作为标准对照。分别构建任意缺失模式（AMP）和单调缺失模式（MMP）下完全随机缺失（MCAR）、随机缺失（MAR）和非随机缺失（NMAR）六种缺失数据集，并使缺失率分别为10%、20%、30%、40%和50%，运用删除法、单一填补法、多重填补法和EM算法进行处理。结果 在AMP下，当MCAR和MAR时，低缺失率（≤10%）下所有方法的效果均较好；随着缺失率的增大，只有多重填补法的效果令人满意。在MMP下，当MCAR和MAR时，只有线性回归法和预测均数匹配法的效果较好。多重填补法的缺点是在一定程度上高估系数的变异程度。另一方面，填补方法对结果的影响远超过填补次数对结果的影响。当NMAR时，所有方法都无法取得较好的处理效果。结论 对于纵向缺失资料，多重填补法仍是一种较为理想的处理方法。

纵向缺失资料 缺失模式 缺失机制 多重填补

缺失数据是生物医学科研中经常碰到的一个问题，在调查研究和临床试验研究中尤为常见。目前对缺失数据的常用处理方法包括直接删除含缺失数据的观测（以下简称删除法）、单一填补法、多重填补法、EM算法等［1］。以往的研究认为，多重填补法考虑了数据缺失的不确定性，相对其他方法具有较大优势，因此在应用中很受研究者的青睐［2-3］。然而，通过查阅文献发现，大部分研究是基于横断面缺失资料展开的，对于纵向缺失资料少有涉及。近期，国外有研究发现多重填补法处理纵向缺失资料的效果并不理想［4-5］，从而动摇了多重填补法在处理缺失数据中的地位。

因此，本文针对纵向缺失资料，考察删除法、单一填补法、多重填补法和EM算法在处理任意缺失模式（arbitrary missing pattern，AMP）及单调缺失模式（monotone missing pattern，MMP）下完全随机缺失（missing completely at random，MCAR）、随机缺失（missing at random，MAR）及非随机缺失（not missing at random，NMAR）机制的效果，对各种方法的处理效果进行综合比较，为研究人员处理纵向缺失资料提供理论支持和帮助。

方法简介

1.删除法（deletion）

删除法是大多数软件默认的处理缺失数据的方法，即删除所有存在待分析变量缺失情形的观测。

2.单一填补法［6］

单一填补法是指用一个确定的值填补缺失值，使原来含有缺失值的数据集形成完整数据集，再按处理完整数据集的方法对其进行处理。常用的单一填补法包括均值填补法（mean imputation）、随机抽取填补法、回归填补法、热平台填补法、最近邻填补法、末次观测结转法（last observation coming forward，LOCF）等。

3.多重填补法［7］

多重填补法是Rubin于1978年提出来的一种相对复杂的缺失数据填补方法。该方法的基本思想是对每一个缺失值产生一系列可能的填补值，从而形成若干个完整的数据集，再用分析完整数据集的方法对每一个填补后的数据集进行分析，最后把分析得到的若干个结果进行综合，从而得到最终的分析结果。常用的多重填补法包括适用于单调缺失模式的线性回归法（regression）、预测均数匹配法（predicted mean matching，PMM）、趋势得分法（propensity score，PS）以及适用于任意缺失模式的马尔科夫链蒙特卡罗法（Markov Chain Monte Carlo，MCMC）等。

4.EM 算法［8］

EM算法是一种迭代运算，包括预测步（E步）和估计步（M步）。预测步是给定未知参数的某个估计值，预测充分统计量中有关缺失数据的部分；估计步是利用预测步得到的充分统计量计算参数最大似然估计的校正值。该过程反复迭代，直到模型收敛为止。

5.多元正态分布假设［9］

多元正态分布是多元定量资料最常见的概率模型，大多数处理多元定量资料的方法都建立在多元正态分布的基础上，因此在处理缺失数据时一般也假定资料满足多元正态分布。然而在现实中数据并不总是满足多元正态分布，尽管如此，正态模型在大多数时候依然是可行的。原因包括以下几点：首先，可以通过合适的数据变换使其满足正态假设；其次，如果某些完整变量（即不存在缺失数据的变量）不满足正态分布，只要能用完整变量的线性方程构建不完整变量使其满足条件正态分布，并且参数推断也仅基于这种条件分布之上，那么多元正态分布模型依然可行；最后，即便缺失变量不满足正态分布，只要缺失信息不是很大，多重填补的推断依然稳健。

模拟分析

1.数据集的构建

运用SAS软件模拟在实际应用中最常见的含一个分组因素和一个重复测量因素的两因素设计纵向资料。假定现欲考察两种处理的效果，将研究对象分成两组，一组使用处理A，一组使用处理B，每组1000例，分别在6个不同的时间点测量某定量指标的取值，比较两种处理的差别。现假设资料服从多元正态分布，两组的均值向量分别是 μA＝（3.0，2.5，2.0，1.7，1.5，1.1）′，μB＝（3.0，2.7，2.5，2.4，2.3，1.1）′，方差与协方差矩阵为：

该方差与协方差矩阵的设置使得各时间点的相关系数呈递减趋势并保持平均相关系数在0.5左右，根据Frison和 Pocock的研究，这些取值是合理的［10］。现用SAS软件的Mixed过程（混合效应模型）对其进行分析，构建结果变量关于分组因素和“时间”两个因素的线性回归方程，将分组因素的回归系数估计值（＾β）以及回归系数标准误（S＾β）作为标准对照。

构造各个时间点上 AMP及 MMP下 MCAR、MAR及NMAR六种数据集，其中MCAR通过随机抽取产生缺失数据得到，MAR通过对两组按1：2的比例分别进行随机抽取产生缺失数据得到，NMAR通过将结果指标在各时间点进行排序，取其中最大的部分数据作为缺失数据得到。保证六种数据集的缺失率分别为10%、20%、30%、40%和50%。

2.处理方法

对于AMP数据集，分别用删除法、单一填补的均值填补法和LOCF、多重填补的MCMC法以及EM算法进行填补后用混合效应模型进行分析，多重填补分别填补3次、5次、10次和15次，以考察不同填补次数对结果的影响；对于MMP数据集，分别用删除法、均值填补法、LOCF法、多重填补的线性回归法、预测均数匹配法和趋势得分法以及EM算法进行填补，再用线性混合效应模型进行分析。该过程循环运行10000次，每种方法得到10000个估计结果。

3.指标比较

用于比较模型处理效果的指标包括：

（1）回归系数估计值的均值及95%置信区间：

（2）回归系数标准误的均值及95%置信区间：

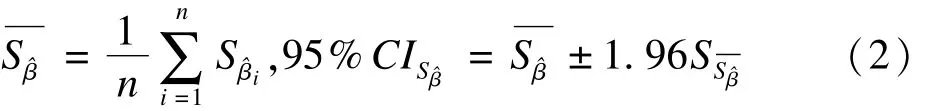
结果比较

图1中，横坐标表示缺失率，分别为10%、20%、30%、40%和50%，纵坐标分别表示回归系数和系数标准误及各自的95%置信区间，虚线表示标准对照，下同。

图1表明，在AMP下，当MCAR和MAR时，低缺失率（≤10%）下所有方法的处理效果均较好；随着缺失率的不断增大，删除法、单一填补法和EM算法的处理效果都不佳，单一填补法甚至不如删除法，其中均值填补法严重低估回归系数的变异程度；而多重填补法的处理效果依然令人满意，当缺失率较低时几乎与标准对照无异，当缺失率达到50%时其回归系数也相当接近标准对照，其缺点是在高缺失率下容易高估回归系数的变异程度，即系数的代表性有待提高。但多重填补的效果并没有随着填补次数的增加而增加。当缺失机制为NMAR时，各种方法的处理效果都不理想。

图1 多种方法处理AMP下三种缺失机制数据集的效果比较

图2 表明，在MMP下，当MCAR和MAR时，删除法、均值填补法、LOCF法、多重填补PS法以及EM算法的结果偏离标准对照较远，而多重填补线性回归法和PMM法则能较好地弥补缺失数据造成的影响。当NMAR时，所有方法的处理效果都不佳。

讨 论

删除法、单一填补法、多重填补法和EM算法是目前处理缺失数据的常用方法。删除法直接删除含缺失值的观测，简单易懂且便于操作。这种以牺牲样本量，舍弃含缺失数据的观测所含信息的做法在数据缺失比例较少时尚可接受，然而随着缺失数据比例的进一步增大，删除法将失去大量的样本信息，从而造成资料无法分析或分析结果产生偏倚，降低效能。若数据缺失比例很大，则可能使样本信息完全无法利用。

单一填补法用一个确定的值代替每一个缺失值，该法同样简单易懂且容易操作，但忽略了缺失数据的不确定性，因而导致数据的变异程度被低估。

多重填补法的基本思想是用一系列可能的值替代缺失值，从而产生多个完整数据集，再对其进行综合分析。该法考虑了缺失数据的不确定性，但相对复杂，操作起来相对困难。

EM算法是求参数极大似然估计的一种迭代算法，是寻求极大似然估计的一种强有力的方法，但其要求数据服从正态分布或混合分布，且M步没有简单的数值计算形式。

图2 多种方法处理MMP下三种缺失机制数据集的效果比较

本文针对纵向缺失数据，通过蒙特卡罗模拟对各种方法的处理效果进行比较，得出以下结论：在任意缺失模式下，当缺失机制为完全随机缺失或随机缺失时，低缺失率（≤10%）下所有方法的效果均较好；随着缺失率的增大，只有多重填补MCMC法的处理效果依然令人满意。在单调缺失模式下，当缺失机制为完全随机缺失或随机缺失时，只有多重填补的线性回归法和预测均数匹配法的填补效果较好，其他方法效果都不佳。多重填补法的缺点是在一定程度上会高估系数的变异程度。另一方面，多重填补的效果并非随着填补次数的增加而增加，填补方法对结果的影响远远超过填补次数对结果的影响。在非随机缺失机制下，所有方法都无法取得较好的处理效果。

虽然多重填补法在处理缺失数据时具有较大优势，我们仍需牢记的一点就是：尽管填补有时能有效缓解数据缺失造成的严重后果，但填补值毕竟不是真实值。正如Dempsters所言：“填补的思想既是诱人的，也是危险的［11］”。因此，在实际科研中，应尽可能地减少数据缺失，确保一手数据的质量。

［1］杨军，赵宇，丁文兴.抽样调查中缺失数据的插补方法.数理统计与管理，2008，27（5）：821-832.

［2］张熙，林燧恒.多重填补在随机干预试验研究中的应用.中国卫生统计，2011，28（5）：537-539.

［3］武建虎，贺佳，贺宪民，等.多变量缺失数据的不同处理方法及分析结果比较.第二军医大学学报，2004，25（9）：1013-1016.

［4］Twisk J，de Boer M，de Vente W，et al.Multiple imputation of missing values was not necessary before performing a longitudinal mixedmodel analysis.Journal of clinical epidemiology，2013，66（9）：1022-28.

［5］Peters SAE，Bots ML，den Ruijter HM，et al.Multiple imputation of missing repeated outcome measures did not add to linear mixedeffects models.Journal of clinical epidemiology，2012，65（6）：686-95.

［6］金勇进.调查中的数据缺失及处理（I）——缺失数据及其影响.数理统计与管理，2001，20（1）：56-62.

［7］SAS／STAT 9.2 User's guide，second edition.Cary，NC：SAS institute Inc，2008：3765-3779.

［8］陈长生，王彤，徐勇勇，等.医学科研中缺失数据的EM估计.第四军医大学学报，2002，23（1）：59-61.

［9］Schafer JL.Analysis of incomplete multivariate data.Florida：CRC Press LLC，1997：194-195.

［10］Frison L，Pocock SJ.Repeated measures in clinical trials：analysis of using mean summary statistics and its implications for design.Statistics in medicine，1992，11（13）：1685-1704.

［11］Dempster AP，Rubin DB.Incomplete data in sample surveys.Vol.II：Theory and Annotated Bibliography.New York：Academic Press，1983：3-10.

Comparative Study of Various Imputation Methods in Dealing with Longitudinal Missing Data

Bao Xiaolei，Gao Hui，Hu Liangping
（Lanzhou General Hospital，Lanzhou Military Area Command（730050），Lanzhou）

Objective To compare the effects of several commonly-used imputation methods in dealing with longitudinal missing data.Methods Simulate the longitudinal data with a classification factor and a repeated-measured factor using Monte Carlo simulation by SAS.Mixed effect model was used to analyze the effect of the longitudinal cohort.The result was used as standard control.Simulation datasets with MCAR，MAR and NMAR under AMPand MMPconditions were constructed，and the missing rate was set to be 10%，20%，30%，40%and 50%，respectively.Deletion method，single imputation method，multiple imputation method and EM method were carried out.The results were then compared with the standard control.Results For MCAR and MAR datasets with AMP，all the methods showed satisfactory results when the rate of missing data remained modest（≤10%）.However，as the percentage increased，the multiple imputation method appeared to be the only optimal strategy.In contrast，for MCAR and MAR datasets with MMP，only the regression method and the predicted mean matching method were efficacious.It has to be noted that multiple imputation method tended to overestimate the variation of regression coefficients.In addition，the imputation methodology played a far more important role than the number of iterations in analyzing the data.For NMAR datasets，all attempted methods were unable to achieve satisfactory results.Conclusion The multiple imputation method was proved desirable in dealing with missing data in longitudinal cohort.

Longitudinal missing data；Missing pattern；Missing mechanism；Multiple imputations

1.兰州军区兰州总医院（730050）

2.中国人民解放军95969部队卫生队

3.北京生物医学统计学咨询中心

郭海强）