使用思维进化算法优化的神经网络建立肾综合征出血热预测模型*

吴 伟 郭军巧 安淑一 任仰武 夏玲姿 周宝森△

使用思维进化算法优化的神经网络建立肾综合征出血热预测模型*

吴 伟1郭军巧2安淑一2任仰武1夏玲姿1周宝森1△

目的 探讨思维进化算法优化的BP神经网络在建立肾综合征出血热发病率预测模型中的应用前景。方法 使用1984-2013年沈阳市的鼠情资料（鼠密度和鼠带毒率）和气象资料（平均气温、降水量和日照时数）作为网络的输入，同年的肾综合征出血热发病率作为网络的输出。把1984-2009年的数据作为训练样本，2010-2013年的数据作为预测样本。分别建立BP神经网络和思维进化算法优化的BP神经网络预测模型，并比较两种模型的拟合和预测效果。结果 对于训练样本和预测样本，思维进化算法优化的BP神经网络的平均绝对误差（MAE）、平均绝对误差百分比（MAPE）以及均方误差平方根（RMSE）均小于未优化的BP神经网络。结论 思维进化算法优化的BP神经网络预测模型的拟合和预测效果均优于未优化的BP神经网络，具有较强的推广应用价值。

肾综合征出血热 思维进化算法 神经网络 预测

目前，人们普遍认为肾综合征出血热（hemorrhagic fever with renal syndrome，HFRS）的发病受到很多因素的影响，如气象因素和动物疫情因素［1-4］。各种影响因素之间又存在错综复杂的联系，因此很难建立结构式的因果模型进行解释。BP神经网络已被广泛用于建立传染病的预警预测模型［5-8］。该方法把未知系统看成是一个黑箱，首先用系统输入输出数据训练网络，使其能够表达该未知函数，然后用训练好的BP神经网络预测系统输出。尽管BP算法具简单、可塑性好等优点，但是在实际使用中也存在一些不足，如收敛速度慢、全局搜索能力弱、容易陷入局部最小等。

随着计算机科学的发展，人们借助适者生存这一进化法则，将计算机科学和生物进化结合起来，逐渐发展形成一类启发式随机搜索的进化算法（evolutionary computation，EC）。该算法存在早熟、结果不可预知等缺陷。针对EC存在的问题，孙承意等人于1998年提出了思维进化算法（mind evolutionary algorithm，MEA）［9］。MEA具有全局寻优能力，可以改善神经网络的收敛速度和精度［10］。为了弥补BP神经网络的不足，本研究拟使用MEA对BP神经网络的初始权值和阈值进行优化，探讨MEA优化后的BP神经网络在建立HFRS预测模型中的应用前景。

资料与方法

1.资料收集 HFRS发病率和鼠情资料来源于辽宁省和沈阳市疾病预防控制中心，收集1984-2013年HFRS年发病率（1／10万）资料，鼠情资料收集1984-2013年每年在监测点采集的鼠密度（%）和鼠带毒率（%）监测数据。气象资料来自于辽宁统计年鉴，选择沈阳市1984-2013年每年的平均气温（℃）、降水量（毫米）和日照时数（小时）。选取1984-2009年的数据作为训练样本，2010-2013年的数据作为预测样本。

2.BP神经网络建立 把每年沈阳市的动物疫情资料（鼠密度和鼠带毒率）和气象资料（平均气温、降水量和日照时数）共5个指标作为样本的输入，同年该地区HFRS的发病率作为样本的输出。所有数据按少隐含层神经元数目的方法，选择使网络具有足够泛化和输出精度的隐含层神经元数目，最后确定为8个隐含层神经元数目。最终，网络结构为5-8-1。隐含层选取logsig作为传递函数，输出层选择tansig作为传递函数，选择trainlm作为训练函数，learngdm作为神经网络权值／阈值学习函数。BP神经网络模型初始化的权值和阈值参数依据Nguyen-Widrow算法随机产生［11］，具体过程如下：w＝0.7×s1／r×randanr（s，r）；d＝w×y+0.7×s1／r×linspae（-1，1，s）.×sign（w（：，1））。其中：s为该层神经元的个数，r为输入向量的维数，y为与输入向量最大值和最小值相关的参数，randanr、linspace和sign为Matlab函数。w和d再经过简单的矩阵运算即为该层权值和阈值的初始参数。根据Nguyen-Widrow算法产生的初始化值，可以使网络层中每个神经元的作用范围近似地在网络层的输入空间均匀分布。最大训练步数为100次，训练目标误差为0.005，学习率为0.1。最后利用训练好的网络进行外推预测，得到的输出值经过反归一化后即为最终预测值。

3.MEA优化BP神经网络的建立［10］

（1）思维进化初始种群的产生 假设神经网络的最大隐含层数为n，每一个隐含层的最大节点数为m。确定了隐含层数和隐含层节点数就确定了神经网络的结构。随机产生N组数作为初始种群，每组数中包含n个元素，代表一个个体（即神经网络结构），每个元素均从隐含层节点数0，1，…，m中选取。本研究BP神经网络结构同上，为5-8-1。

（2）得分函数的确定 本研究选择训练集的均方误差的倒数作为各个个体与种群的得分函数f＝出值，ti表示目标输出，p为训练样本数。

（3）训练权值和阈值 对于每个网络结构，在（0，1）之间以均匀分布产生R组随机数，作为初始的权值和阈值群体。根据网络计算规则，按照得分函数计算每个个体得分，得分最高的q个个体被称为优胜者。误差越小，则认为个体所含权值和阈值信息越好，得分就越高。

（4）子种群趋同过程 分别以每一个优胜者为中心，服从正态分布产生个体，形成M个优胜子种群和T个临时子种群，每个子群体包含w个个体。该正态分布可以表示为N（μ，∑），式中μ是正态分布的中心向量，Σ是该正态分布的协方差矩阵。正态分布的中心就是胜者的坐标，即胜者的权值。本研究的优胜子种群和临时子种群个数均设为5。

（5）子种群异化过程 异化操作是整个解空间内各子群体成为胜者而竞争的过程。通过全局公告版，它记录了各子群体评价函数值以及成熟度，在各个子群体间进行全局竞争，若一个临时子群体的得分高于某个成熟优胜子群体的得分，则该优胜子群体被获胜的临时子群体替代，原优胜子群体中的个体被释放；若一个成熟的临时子群体得分低于任意一个优胜子群体得分，则该临时子群体被废弃，其中的个体被释放。

（6）解析最优个体 当满足迭代停止条件时，思维进化算法结束优化过程。此时，根据编码规则，对寻找到的最优个体进行解析，从而得到对应的BP神经网络的权值和阈值。

（7）训练MEA优化的BP神经网络 MEA优化的BP神经网络的训练参数和未优化的BP神经网络一致。

4.效果评价［12］使用平均绝对误差（MAE）、平均绝对误差百分比（MAPE）以及均方误差平方根（RMSE）三个指标对BP神经网络和MEA优化的BP神经网络的拟合及预测效果进行评价。

5.数据处理 利用Matlab2014b软件中的神经网络工具箱编程构建BP神经网络；编写并调用初始种群产生函数、子种群产生函数和种群成熟判别等函数实现MEA的运算。

结 果

1.未优化的BP神经网络训练情况 未优化的BP神经网络经过14次训练后，其训练误差为0.0047。网络训练误差迭代收敛曲线见图1。

图1 未优化的BP神经网络误差迭代收敛曲线

2.MEA优化的BP神经网络训练情况 MEA优化的BP神经网络初始优胜子种群和临时子种群的趋同过程分别见图2和图3。通过观察图形，我们发现，经过若干次趋同操作，各个子种群均已成熟（得分不再增加）。同时，待优胜子种群和临时子种群成熟后，临时子种群中的子种群3的得分比优胜子种群中的一些子种群得分高，而优胜子种群中的子种群3的得分比临时子种群中的一些子种群得分低，因此需要执行1次异化操作，同时需要补充1个新的子种群到临时子种群中。MEA优化的BP神经网络经过11次训练后，其训练误差为0.0027。网络训练误差迭代收敛曲线见图4。

图2 初始优胜子种群趋同过程

图3 初始临时子种群趋同过程

图4 思维进化算法优化的BP神经网络误差迭代收敛曲线

3.两种模型的拟合和预测效果的比较 两种模型的拟合和预测值见表1。对于训练样本和预测样本，MEA优化的 BP神经网络的 MAE、MAPE和RMSE均小于未优化的BP神经网络（表2）。

表1 两种模型的拟合和预测值比较（单位：1／10万）

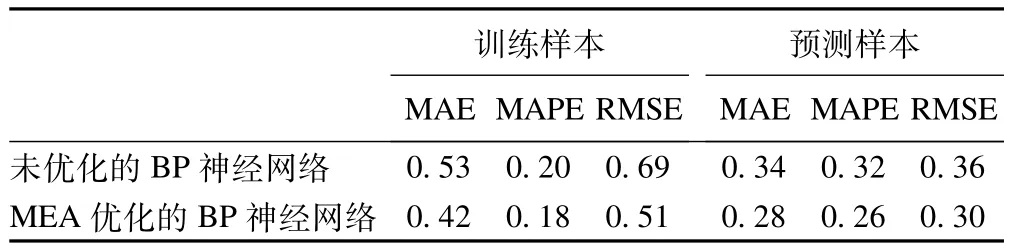
表2 两种模型拟合和预测效果的比较

讨 论

目前为止，很多研究者对HFRS的疫情和流行特征建立了预测预警模型进行分析。其中，多数的方法是使用时间序列分析的方法对HFRS进行研究［13-17］。这些方法把时间序列变量综合替代各种影响因素，对数据资料要求较低，模型的建立过程简单，短期预测精度较高。而对于本研究中的数据，按照上述方法我们未能建立合适的时间序列模型。此外，这些研究中大多都未考虑其他影响因素对出血热发病的影响。根据专业知识判断，在条件允许的情况下，把HFRS发病的影响因素纳入到模型中应该可以提高模型的拟合和预测精度。

MEA是近年来提出的一种新算法，主要通过模拟生物进化过程中人类思维进化的方式。它借鉴了遗传算法的“群体”与“进化”的思想，将群体划分为若干子群体，提出了“趋同”与“异化”两种操作，并且这二者的作用是非对立的。“趋同”操作对系统从环境得到局部信息加以开采，迅速搜索局部最优。而“异化”操作在整个解空间进行搜索，选择较优的个体作为中心创建新的临时子群体［18］。因而，MEA具有全局寻优的能力，将其用于优化神经网络的权值和阈值后，可有效改善神经网络收敛速度和收敛精度。本研究在使用BP神经网络建立沈阳市HFRS预测模型过程中，使用MEA在神经网络的权值和阈值范围内，通过多次的“趋同”与“异化”操作进行全局寻优，将得到的全局最优解应用于BP神经网络的初始值中。研究结果表明，使用MEA优化的BP神经网络方法可以在一定程度上改善模型的收敛速度，并且提高拟合和预测的准确性，具有一定的应用前景。

MEA在变压器故障诊断［19］和电厂主蒸汽温度控制［20］等方面已进行大量相关应用，并取得了较好的效果。目前为止，该方法在医学领域的应用并未见到相关报导。本研究首次把MEA应用于传染病领域，虽然本次研究中优化后的BP神经网络对于HFRS建模效果尚可，但是此方法是否适用于其他疾病需要开展后续进一步的深入研究进行论证。此外，基于MEA优化神经网络的方式主要有三种：优化神经网络的权值和阈值、优化神经网络的结构和优化神经网络的学习规则。本研究只是针对神经网络权值和阈值的优化进行了深入的研究，在其他两个方面进行优化的研究仍然有不足，后续研究可以考虑三种方法结合使用，观察其对所建预测模型的影响。再次，目前MEA作为一种比较新的理论，这方面的资料还不是很完善。同时对于群体的规模设置、优胜子群体和临时子群体的个数和迭代进化停止条件等还没有成熟的理论指导，现在多是根据个人的经验进行确定，因此我们仍需对MEA进行深入研究。

［1］罗雷，王鸣，周端华，等.气候因子与肾综合征出血热发生及鼠密度关系分析.现代预防医学，2005，32（3）：205-222.

［2］刘静，王洁贞，薛付忠，等.肾综合征出血热发病率与气象因素关系的研究.中国卫生统计，2006，23（4）：326-329.

［3］罗成旺，陈化新.肾综合征出血热流行因素的影响研究.中国媒介生物学及控制杂志，2003，14（6）：451-454.

［4］吴荣军，胡晓抒，郑有飞，等.肾综合征出血热与气象因子相关性分析及其预报研究.中国媒介生物学及控制杂志，2005，16（2）：118-120.

［5］黎健，顾君忠，毛盛华，等.BP人工神经网络模型在上海市感染性腹泻日发病例数预测中的应用.中华流行病学杂志，2013，34（12）：1198-1202.

［6］徐学琴，徐玉芳，朱明军，等.基于逆传播神经网络的麻疹短期发病预测研究.中国全科医学，2013，16（29）：3488-3490.

［7］刘文东，吴莹，艾静，等.BP神经网络在痢疾发病趋势预测中的应用研究.中国卫生统计，2012，29（6）：801-804.

［8］杨佳琦，陈露菲，陈淑红，等.BP神经网络在肾综合征出血热发病率预测中的应用.中华疾病控制杂志，2012，16（8）：717-720.

［9］Sun Chengyi，Sun Yan，Wei Lijan.Mind-Evolution-Based Machine Learning：Framework and the Implementation of Optimization.Proc.of IEEE Intelligent Conference on Intelligent Engineering Systems，1998：355-359.

［10］张建军，李秀广，武娟.基于思维进化BP网络的电力系统暂态稳定事故筛选.电气技术，2010（5）：41-44.

［11］刘鲭洁，陈桂明，刘小方，等.BP神经网络权重和阈值初始化方法研究.西南师范大学学报（自然科学版），2010，35（6）：137-141.

［12］张兴裕，张韬，刘元元，等.小波神经网络在肾综合症出血热发病率预测中的应用.中国卫生统计，2012，29（6）：864-865.

［13］陈叶，白杉，陈慧中，等.ARMA模型对肾综合征出血热发病趋势预测的拟合研究.现代预防医学，2008，35（8）：1414-1415.

［14］刘洁，曲波，何钦成.应用GM（1，1）模型对全国1999-2009年肾综合征出血热疫情分析及预测.中国媒介生物学及控制杂志，2011，22（3）：248-250.

［15］吴伟，关鹏，郭军巧，等.GM（1，1）灰色模型和 ARIMA模型在HFRS发病率预测中的比较研究.中国医科大学学报，2008，37（1）：52-55.

［16］黄德生，郭海强，沈铁峰，等.SARIMA模型在肾综合征出血热发病率预测中的应用.数学的实践与认识，2009，39（23）：100-106.

［17］郭海强，丁海龙，曲波，等.应用ARIMA模型对全国2004-2009年肾综合征出血热疫情分析及预测.中国人兽共患病学报，2010，26（12）：1137-1140.

［18］尚彦维.基于思维进化算法的单相电机矢量控制系统.太原：太原理工大学硕士，2009.

［19］高金兰，陶国彬，赵玉峰.思维进化优化模糊神经网络的变压器故障诊断.科学技术与工程，2011，11（13）：2957-2961.

［20］王新亚.基于MEA-BP神经网络的主汽温控制系统的研究.山西焦煤科技，2009（3）：13-15.

Application of Mind Evolutionary Algorithm Optimized Neural Network Model to Predict the Incidence of Hemorrhagic Fever with Renal Syndrome

Wu Wei，Guo Junqiao，An Shuyi，et al
（Department of Epidemiology，School of Public Health，China Medical University（110122），Shenyang）

Objective To explore the application prospect of mind evolutionary algorithm optimized neural network model in building prediction model of hemorrhagic fever of renal syndrome.Methods Rat epidemic information including rodent density and viral carriage of rodents and meteorological data including average temperature，precipitation and sunshine duration from 1984 to 2013 in Shenyang city were used as the input of neural network.The incidence of HFRSin the same year was used as the output of neural network.Data from 1984 to 2009 were selected as training sample，while data from 2010 to 2013 were selected as predicting sample.BPneural network and MEA optimized BPneural network were built respectively.Fitting and forecasting effect were compared between the two models.Results For the training sample and predicting sample，the mean absolute error，mean absolute percentage error and root mean square error of mind evolutionary algorithm optimized BPneural network were smaller than that of BP neural network.Conclusion MEA optimized BP neural network fitting and forecasting the HFRS incidence better than BP neural network，which is of great application value for the prevention and control of HFRS.

Hemorrhagic fever with renal syndrome；Mind evolutionary algorithm；Neural network；Predict

*国家自然科学基金项目（No.81202254；No.30771860）资助

1.中国医科大学公共卫生学院（110122）

2.辽宁省疾病预防控制中心

△通信作者：周宝森，E-mail：bszhou＠mail.cmu.edu.cn

郭海强）