一水力深穿透射孔对压裂裂缝形态影响的数值模拟

仲冠宇, 王瑞和, 周卫东, 陈贵春, 万春浩

(中国石油大学石油工程学院,山东青岛 266580)



一水力深穿透射孔对压裂裂缝形态影响的数值模拟

仲冠宇, 王瑞和, 周卫东, 陈贵春, 万春浩

(中国石油大学石油工程学院,山东青岛 266580)

基于各向异性弹性力学,结合流体力学理论,建立水力深穿透射孔条件下各向异性地层中垂直裂缝扩展的力学模型,基于最大周向应力准则建立裂缝扩展路径的计算方法,利用牛顿迭代法求解数值模型,并通过算例验证模型及求解方法的正确性。结果表明:裂缝转向半径随着射孔长度及射孔角度的增加而增大,随着压裂液黏度及排量的增加而增大;对称布孔方式优于单侧布孔方式,裂缝转向半径随着弹性模量各向异性差值的增加而增大,随着弹性模量的增大而增加。

水力深穿透射孔; 水力压裂; 裂缝扩展形态; 弹性模量; 各向异性

水力深穿透射孔技术是一项新的油气井增产技术[1-3],其工作原理是在套管开小窗后利用水力钻头的高压射流实现径向钻孔及水平钻进,形成水平孔眼。与常规射孔技术相比,水力深穿透射孔技术所形成的孔眼深度大、孔径大,降低了射孔压实作用,有利于引导裂缝发展及油气井增产,因此在水力压裂领域中具有广阔的应用前景。裂缝形态是影响油气井单井产能的重要因素,而孔眼形态对裂缝的发展形态有重要的影响作用,如何优化水力深穿透射孔参数,引导裂缝发展,对油气井增产效果意义重大。不少学者针对射孔对裂缝发展形态的影响展开了研究。Jeffery等[4-6]通过室内试验研究了孔眼形态对裂缝形态的影响规律,但由于模型尺寸较小,难以应用于实际。也有学者[7-11]通过数值模拟方法分析了射孔对裂缝发展形态的影响,但是研究均从各向同性弹性力学出发,限制了研究成果的适用性,而且针对水力深穿透射孔技术所形成的深孔眼条件下的研究基本未涉及。鉴于此,笔者在前人研究的基础上,依据各向异性弹性力学、流体力学等基本理论,建立各向异性地层中水力深穿透射孔条件下垂直裂缝发展形态的计算模型,并研究裂缝形态的影响因素,为水力深穿透射孔技术在压裂作业中的应用提供理论指导。

1 水力深穿透射孔条件下裂缝扩展模型的建立

1.1 物理模型及基本假设

水力深穿透射孔技术可形成大直径深孔。在孔眼的引导作用下,压裂裂缝沿孔眼起裂并扩展,形成双翼弯曲缝。考虑水力深穿透射孔技术在直井中应用较多,为深入研究孔眼形态对近井壁裂缝形态的影响,沿水平方向截取单位厚度的地层为研究对象,建立水力深穿透射孔条件下直井垂直裂缝扩展的平面应变模型,如图1所示。射孔方向与最大主应力的夹角为β,水平最大主应力为σH,水平最小主应力为σh。

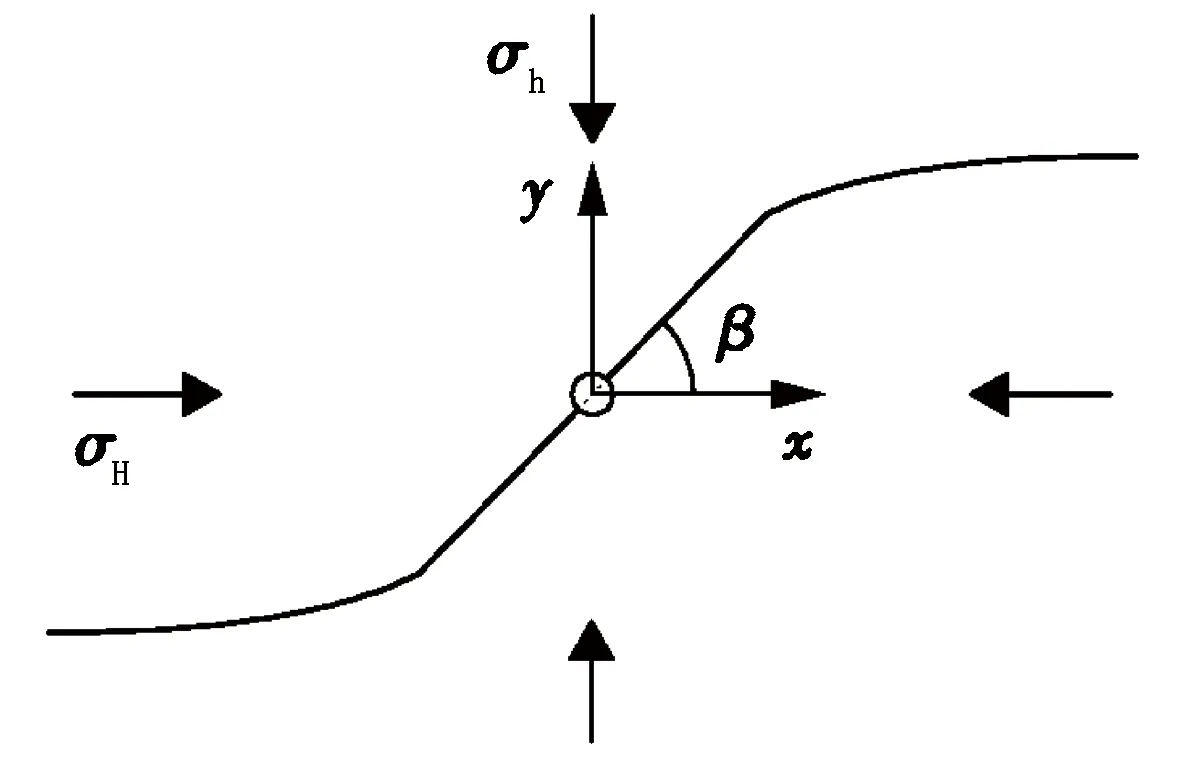
图1 模型示意图

为降低模型的复杂程度,假设:压裂液为不可压缩牛顿流体,其压力在高度方向上保持不变;不考虑岩石及压裂液温度对裂缝发展形态的影响;水泥环第一界面、第二界面胶结良好。

1.2 基本方程

(1)裂缝宽度表达式。考虑裂缝边界单元,令相对位移Δuj=uj(C+)-uj(C-),根据边界元方法可以得到各向异性地层中裂缝面间的相对位移与应力的关系[12-14]为

(1)

式中,Csdik为刚度矩阵单元,具体内容见文献[15];Tij为拉力的核函数;nd为裂缝面外法线与α方向夹角的余弦;φm,l为第m个裂缝单元第l个节点的二次插值函数;NC为裂缝单元个数;pw,s为第w个裂缝单元s方向上的远场地应力和缝内压力的合力;Δuml,j为第m个裂缝单元上下表面在第l个节点处j方向上的相对位移。

(2)压降方程。对于牛顿型流体,压降方程[16]为

(2)

式中,p为缝内压力;q为缝内流量;h为裂缝高度;μ为流体黏度;wf为裂缝宽度。

(3)连续性方程。当压裂液流体通过裂缝的某一裂缝单元时,根据质量守恒原则,得

Vflow=ΔV+Vleak.

(3)

其中

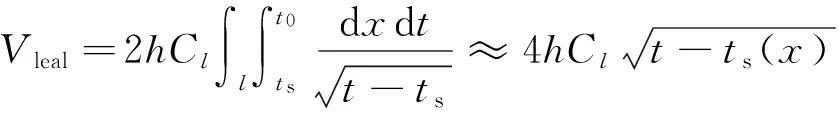
式中,Vflow为裂缝单元的流量变化;ΔV为裂缝单元的体积变化;Vleak为滤失体积;l为裂缝单元长度;Cl为滤失系数;ts(x)为缝长x位置处压裂液开始滤失的时间。

2 水力深穿透射孔条件下裂缝扩展数值模型的求解

2.1 各向异性地层中裂缝扩展路径计算

各向异性材料裂缝尖端应力场计算公式与各向同性材料存在很大差别,故基于各向同性力学所推导的裂缝扩展路径计算方法并不适用于各向异性地层中,本文中基于各向异性弹性力学建立各向异性地层中裂缝扩展路径的求解方法。

对于各向异性材料,应力强度因子KⅠ和KⅡ可通过裂缝尖端的相对位移Δu1和Δu2求解[17],即

(4)

其中

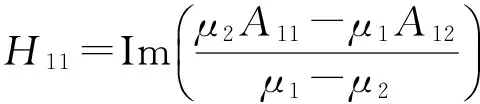
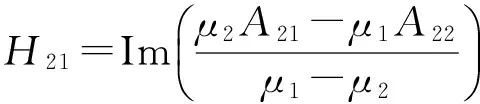
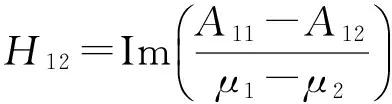
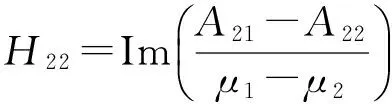
式中,μ1、μ2、A11、A12、A21和A22为各向异性弹性体相关的材料参数[15,18]。

裂缝尖端应力场可用应力强度因子KⅠ和KⅡ表示为

(5)

(6)

(7)

式中,σx′、σy′和τx′y′为以裂尖扩展方向为x′轴的局部坐标系下的应力;θ和r分别为任意一点距裂尖的极角和极径。

极坐标条件下裂缝尖端的周向应力可表示为

σθ(θ)=σx′sin2θ-2τx′y′sinθcosθ+σy′cos2θ.

(8)

根据最大周向应力理论,裂缝的扩展角度为周向应力达最大值的方向,因此可将扩展路径的求解问题转换为最优化问题,即

(9)

根据所求解的最大周向应力的方位角,可求出裂缝的等效应力强度因子的近似解[19-20],即

(10)

式中,σθ为最大周向应力;Ke为等效应力强度因子。

根据断裂力学,当裂缝尖端的等效应力强度因子大于岩石的Ⅰ型断裂韧性时,裂缝开始扩展[21],由此可建立各向异性地层中裂缝扩展的判断准则,即

Ke≥KIc.

(11)

式中,KIc为岩石的Ⅰ型断裂韧性。

2.2 基本方程的离散化处理

式(1)可改写为

(12)

由于矩阵Ass和Ann为可逆矩阵,化简式(12)可得到裂缝宽度与远场地应力、缝内压力的关系式为

w=M-1N,

(13)

(14)

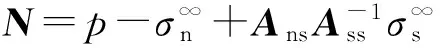
(15)

根据式(2)可求得压降与流量的关系方程为

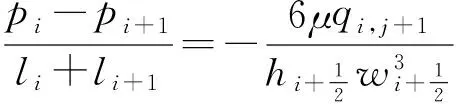
(16)

式中，qi,i+1为第i个裂缝单元流入第i+1个裂缝单元的流量。

式(3)可简化为

∑qijΔt/h=(wi,t+Δtli,t+Δt-wi,tli,t)+

(17)

2.3 模型的求解

式(17)构成一组关于缝内压力、流量、裂缝宽度的方程组,为了便于求解,将式(13)、(16)代入式(17)中,则式(17)可化为

Ω(p)=0.

(18)

其中

p=[p1p2p3…pn]T,

Ω(p)=[Ω1(p)Ω2(p)Ω3(p) …Ωn(p)]T.

式(18)为复杂的非线性偏微分方程组,利用数值方法求解。牛顿迭代法是一种常用的非线性方程组求解方法,具有收敛速度快、编程简单等优势[22],因此在本文中采用该方法求解缝内压力分布,具体方法如下。

设pk为式(18)的第k次近似解,将Ω(p)在pk处进行泰勒展开,可构造牛顿迭代式:

(19)

式中,Ω′(pk)为Ω(p)的Jacobi矩阵在pk处的值。

在每一时间步内从初始值p0出发,通过式(19)反复迭代,当精度满足要求时停止。

由此,本文中提出裂缝形态的求解方法,具体过程如图2所示。先假设一个时间步长,计算该时间步长下的缝内压力,求得裂缝尖端的应力强度因子并判断其是否满足扩展要求,若满足,则根据所计算的裂缝扩展方位角在裂缝尖端延伸一裂缝单元,进入下一时间步的计算。

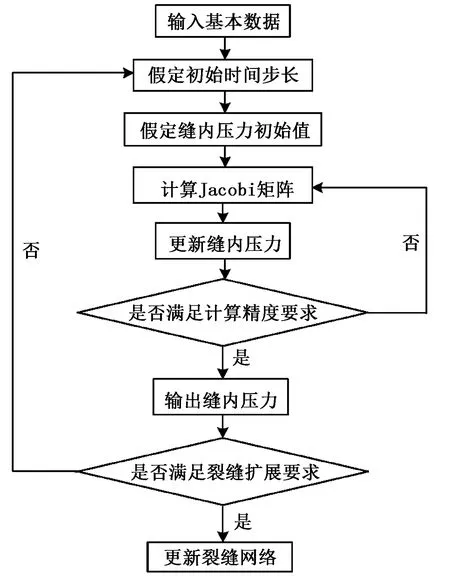
图2 计算流程

2.4 模型验证

已有Adachi等[16]学者从各向同性弹性力学出发建立了考虑压裂液滤失的平直双翼裂缝扩展数学模型。为便于验证上述裂缝扩展模型及计算方法的正确性,计算参数取特殊情况:Ex=Ey,vxy=vyz=vxz,裂缝的起裂方向为水平最大主应力方向,则本模型可近似为基于滤失效应的各向同性介质中平直双翼缝扩展模型,将此条件下本文的计算结果与Adachi等[16]的计算结果进行比较。计算参数为弹性模量为8 GPa,泊松比为0.3,流量为2 m3/min,滤失系数为8×10-5m/s0.5。

图3为计算结果与Adachi等[16]模型的结果对比。可以看出,基于本文模型所求解的缝口净压力、缝口宽度及裂缝半长的数值解与Adachi等[16]模型的计算结果吻合较好,说明本文模型可较准确地模拟裂缝扩展情形,因此可用于水力深穿透射孔条件下裂缝形态的分析。

图3 计算结果与Adachi模型对比

3 近井壁裂缝形态的敏感性分析

为探讨各向异性地层中水力深穿透射孔条件下裂缝形态的影响因素,取某储层参数进行影响因素分析。计算参数为:Ex=8.03 GPa,Ey=6.99 GPa,vxy=0.493,σH=11.12 MPa,σh=9.9 MPa,Q0=6 m3/min。

3.1 孔眼方向

为方便表述,定义孔眼方向为孔眼轴线与最大水平井主应力方向的夹角。图4为裂缝缝内压力和裂缝宽度云图。由图4(a)可以看出,当径向孔眼方向与水平最大主应力方向成一定角度时,裂缝沿孔眼方向起裂并延伸一段距离后,在远场最大地应力作用下逐渐转向水平最大主应力方向扩展,形成弯曲缝。这是根据最小能量原理,裂缝沿阻力最小的方向扩展,当裂缝沿平行于水平最大主应力方向扩展时,由于所克服的应力为水平最小主应力,扩展阻力最小,所以裂缝的扩展方向均由射孔方向逐渐转向水平最大主应力方向。

传统的双翼裂缝模型认为,裂缝宽度在缝口处最大,并随着与缝口距离的增大而减小。由图4(b)可以看出,当裂缝由射孔方向逐渐转向水平最大主应力方向扩展时,裂缝宽度呈现先减小后增大的趋势。这是由于裂缝张开时所克服的阻力为最大主应力和最小主应力的合力,裂缝与水平最大主应力方向的夹角越大,水平最小主应力占总正应力的分量越小,裂缝的宽度随之减小。当水力深穿透射孔的射孔角度过大时,裂缝宽度过小,易出现堵缝内压力过高、砂堵等复杂情况,为了提高深穿透射孔辅助压裂的施工效率,应减小或避免近井壁弯曲裂缝等复杂情况。

图5为其余参数不变的情况下,不同射孔角度条件下裂缝的发展形态。由图5可以看出,裂缝的转向半径随着射孔角度的增加而增大。这是由于当射孔方向与水平最大主应力方向夹角较小时,裂缝延伸较小距离后即可转向水平最大主应力方向扩展,因而转向半径较小,反之亦然。

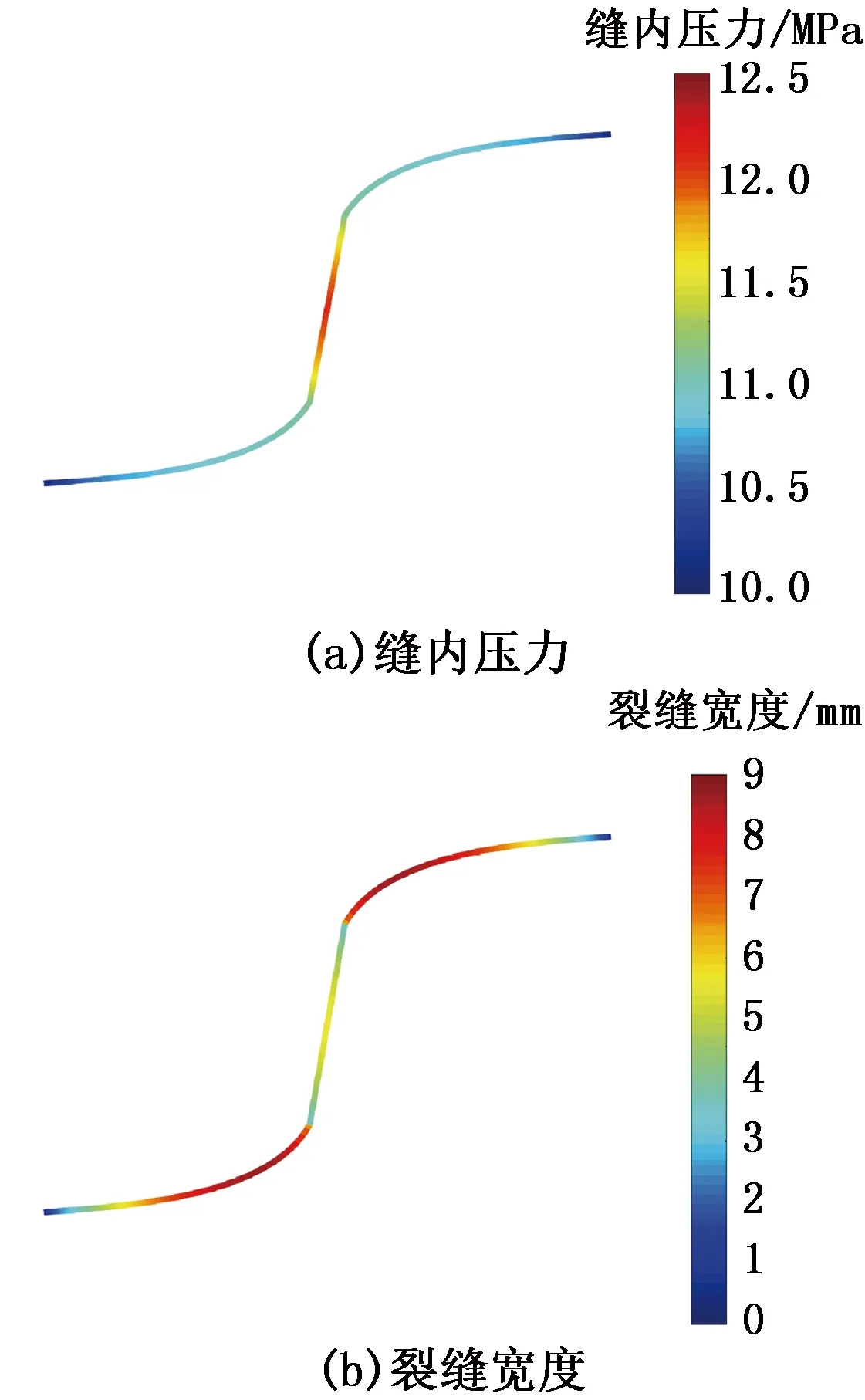
图4 裂缝宽度及缝内压力分布

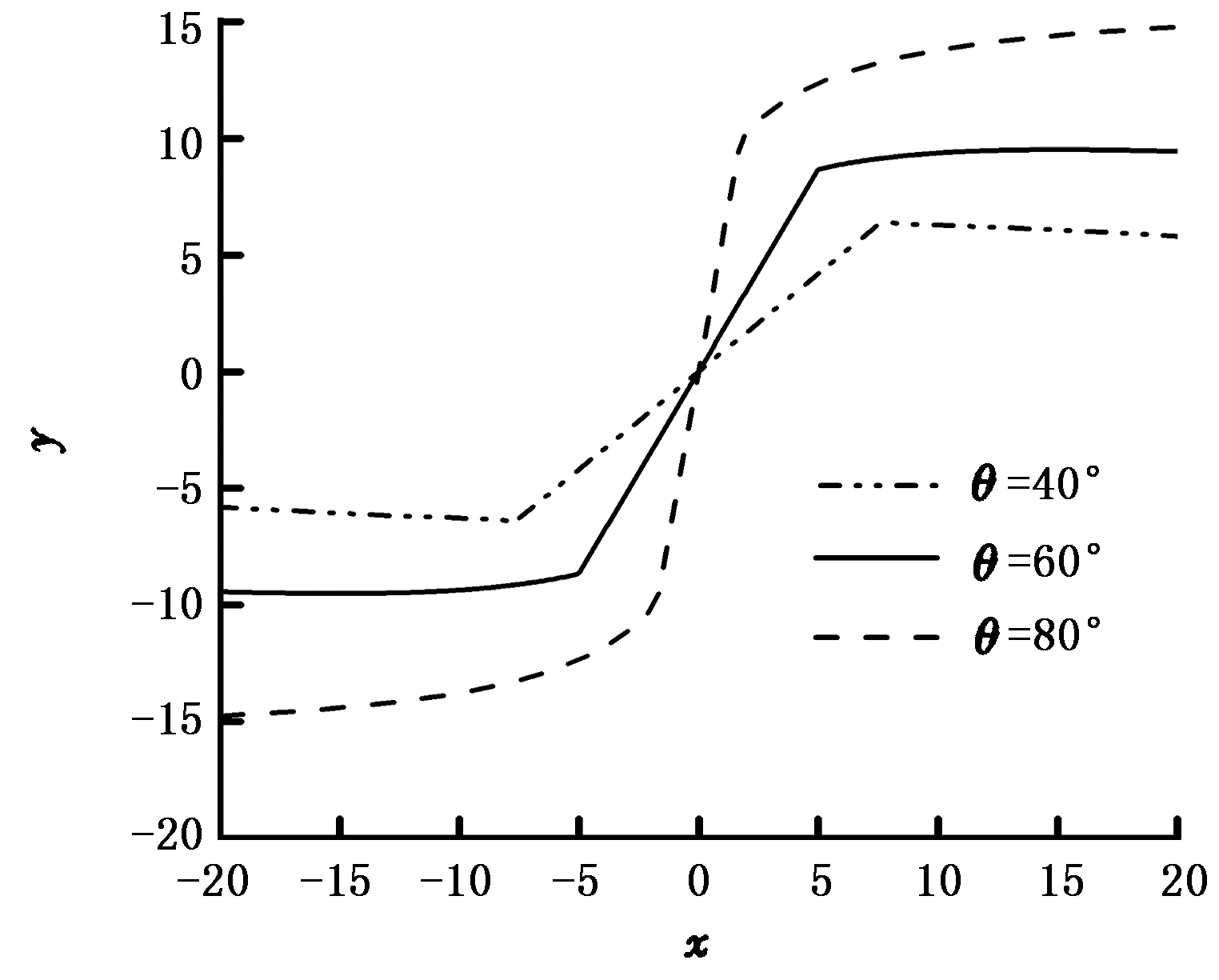
图5 不同孔眼方向下的裂缝发展形态

3.2 孔眼长度

图6为其余参数不变时,不同孔眼长度条件下的裂缝发展形态。由图6可以看出,随着孔眼长度的增大,裂缝转向半径增加。这是由于在长水平孔眼引导裂缝扩展的作用下,裂缝沿偏离最大主应力的方向延伸较长距离后才可逐渐转向至水平最大主应力方向,因此裂缝的转向半径随射孔长度的增加而增大。

图6 不同孔眼长度下的裂缝发展形态

3.3 弹性模量

图7为其余参数不变时,不同弹性模量条件下裂缝的发展形态。由图7可以看出,随着弹性模量的增大,裂缝的转向半径减小。这是由于当弹性模量增大时,由裂缝所产生的诱导应力增加,对近井壁原始地应力场产生了一定的影响,使近井壁区域的水平应力差异性逐渐减小,裂缝更容易发生转向。裂缝转向半径过小会导致压裂液流动阻力增大,不利于加砂改造。在煤层气储层等低弹性模量地层中,控制水力深穿透射孔方向并采用合理的压裂施工设计,显得尤为重要。

图7 不同弹性模量的裂缝发展形态

3.4 弹性模量各向异性

图8为其余参数不变时,弹性模量各向异性对近井壁裂缝形态的影响。由图8可以看出,随着垂直方向上弹性模量的增大,裂缝的转向半径增大。这是由于不同方向上弹性模量的变化改变了裂缝所产生的诱导应力分布,减小了近井壁水平地应力差,降低了裂缝转向的阻力,因此转向半径随着弹性模量各向异性比值的增加而增大。

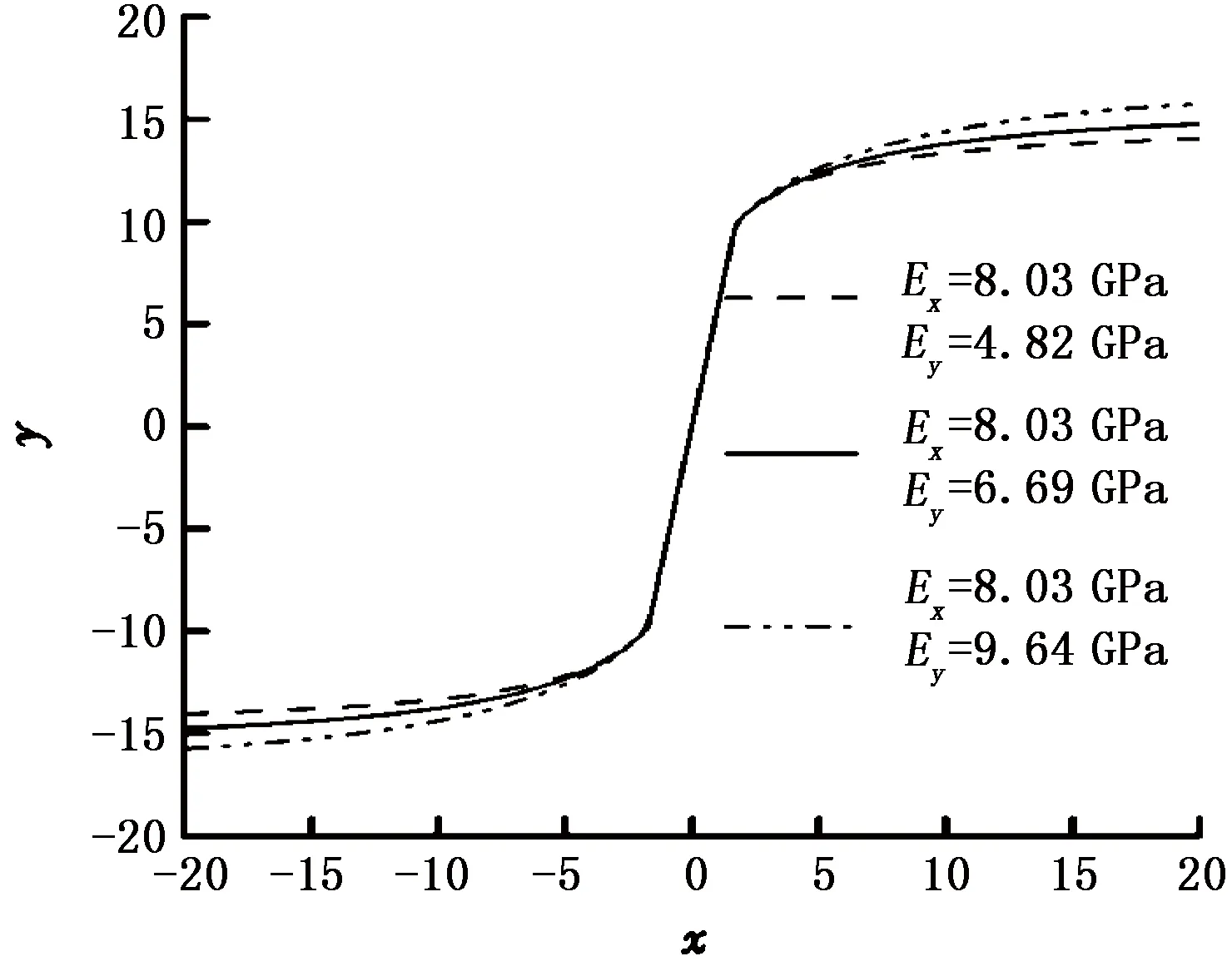
图8 不同弹性模量各向异性条件下的裂缝发展形态

3.5 孔眼数量

图9为其余参数不变时,单侧布孔条件下的裂缝的缝内压力及宽度云图。由图9可以看出,缝口宽度并不是最大,井筒附近的裂缝宽度随着与井眼距离的增加而增大,这与图4(b)中对称布孔条件下的裂缝宽度分布存在区别。一方面,过小的缝口宽度增大了压裂液局部摩擦阻力,不利于支撑剂的运移;另一方面,缝口宽度的减小不利于油气运移,会使单井产量降低,因此单侧布孔的水力深穿透射孔方式不利于油气井增产。

图9 单侧布孔条件下裂缝宽度及缝内压力分布

图10为其余参数不变时,多孔眼条件下的近井壁裂缝形态。其中,4条径向水平井孔眼与水平最大主应力的夹角分别为45°、135°、225°和315°。由图10可以看出,在压裂液压力作用下孔眼根部由于应力集中而产生裂缝并扩展,从而产生多裂缝的复杂情况,因此增加射孔孔眼的数量会增大发生多裂缝的可能性。

图10 多孔眼条件下裂缝形态

3.6 排 量

图11为其余参数不变时,不同排量条件下裂缝的发展形态。由图11可以看出,排量对裂缝发展形态有重要的影响,随着排量的增大,裂缝转向半径增大。这是由于一方面随着排量的增加,压裂液的能量增加,使压裂裂缝有足够的能力克服远场地应力扩展,另一方面,随着排量的增加,压力波及范围增大,减小了水平主应力差,使裂缝更容易发生转向。

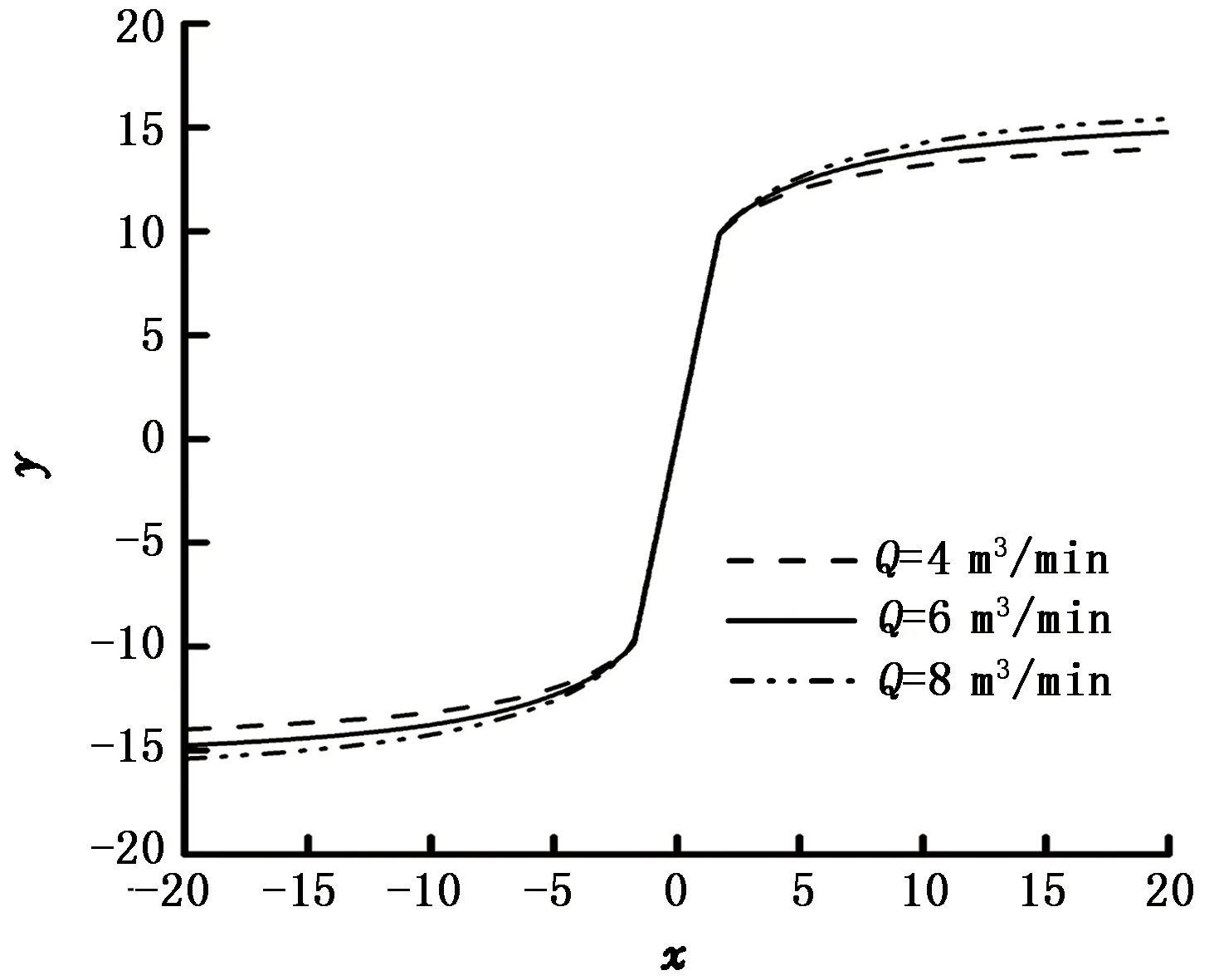
图11 不同排量下的裂缝发展形态

3.7 黏 度

图12为其余参数不变时,不同黏度条件下裂缝的发展形态。由图12可以看出,随着黏度的增加,裂缝转向半径增大。这是由于随着黏度的增加,沿程摩阻增大,进而引起缝内压力增加。当缝内压力较大时,裂缝所产生的诱导应力场增强,减小了一定范围内原始地应力场的水平主应力差,促使裂缝发生转向,因此裂缝的转向半径随着黏度的增加而增大。

图12 不同黏度的裂缝发展形态

4 结 论

(1)基于各向异性弹性力学和边界元方法,结合流体力学理论,建立了各向异性地层中水力深穿透射孔条件下垂直裂缝扩展的平面应变模型,通过最大周向应力准则提出了裂缝扩展路径的计算方法,并通过牛顿迭代法建立了裂缝扩展模型的数学求解方法,算例验证了所建立模型的正确性。

(2)裂缝转向距离随着弹性模量各向异性比值的增加而增大,裂缝转向半径随着弹性模量的增大而增大。裂缝转向半径随着射孔长度及射孔角度的增加而增大。单侧布孔不利于压裂作业,孔眼数目过多易造成多裂缝的复杂情况。增大压裂液的黏度及排量可增大压裂裂缝的转向半径。

[1] 王立军,贺风云,吴春玉,等. 深穿透水力射流射孔产能的计算及影响因素[J]. 大庆石油学院学报,2001,25(2):22-24. WANG Lijun, HE Fengyun, WU Chunyu, et al. Calculation method and affecting factors of productivity for deep penetrating perforation with hydraulic jet flow[J].Journal of Daqing Petroleum Institute, 2001,25(2):22-24.

[2] 吴秀田,田树宝,张鹏,等. 水力射流深穿透射孔产能分析及参数优化[J]. 石油钻采工艺,2010,32(5):74-78. WU Xiutian, TIAN Shubao, ZHANG Peng, et al. Productivity analysis and parameter optimization for deep hydraulic jet perforation wells[J]. Oil Drilling & Production Technology, 2010,32(5):74-78.

[3] 党文辉,马宏伟,陈建林,等. 套管内钻孔深穿透径向井技术[J]. 石油钻采工艺,2013,35(1):45-47. DANG Wenhui, MA Hongwei, CHEN Jianlin, et al. Research on deep penetration of radial well hole-drilling in casing[J]. Oil Drilling & Production Technology, 2013,35(1):45-47.

[4] JEFFREY R G, CHEN Z R, ZHANG X, et al. Measurement and analysis of full-scale hydraulic fracture initiation and reorientation[J]. Rock Mechanics and Rock Engineering, 2015,48(6):2497-2512.

[5] ZENG Z, ROEGIERS J, GRIGG R. Imaging the initiation of asymmetrical hydraulic fractures in laboratory experiments[R]. SPE 84578-MS, 2003.

[6] ZHU H Y, DENG J G, LIU S J, et al. Hydraulic fracturing experiments of highly deviated well with oriented perforation technique[J]. Geomechanics & Engineering, 2014,6(2):153-172.

[7] ABDOLLAHIPOUR A, MARJI M F, BAFGHI A Y, et al. Simulating the propagation of hydraulic fractures from a circular wellbore using the displacement discontinuity method[J]. International Journal of Rock Mechanics and Mining Sciences, 2015,80:281-291.

[8] AGHIGHI M A, RAHMAN S S, RAHMAN M M. Effect of formation stress distribution on hydraulic fracture reorientation in tight gas sands[R]. SPE 122723-MS, 2009.

[9] SEPEHRI J, SOLIMAN M Y, MORSE S M. Application of extended finite element method to simulate hydraulic fracture propagation from oriented perforations[R]. SPE 173342-MS, 2015.

[10] ZHANG X, JEFFREY R G, BUNGER A P, et al. Initiation and growth of a hydraulic fracture from a circular wellbore[J]. International Journal of Rock Mechanics and Mining Sciences, 2011,48(6):984-995.

[11] 张广清,陈勉,王强.斜井井筒附近水力裂缝空间转向模型研究[J].石油大学学报(自然科学版),2004,28(4):51-55. ZHANG Guangqing, CHEN Mian, WANG Qiang. Three-dimensional model for space reorientation of hydraulic fractures near deflecting well bore[J]. Journal of the University of Petroleum, China (Edition of Natural Science), 2004,28(4):51-55.

[12] CHEN C, PAN E, AMADEI B. Fracture mechanics analysis of cracked discs of anisotropic rock using the boundary element method[J]. International Journal of Rock Mechanics and Mining Sciences, 1998,35(2):195-218.

[13] PAN E, AMADEI B. Fracture mechanics analysis of cracked 2-D anisotropic media with a new formulation of the boundary element method[J]. International Journal of Fracture, 1996,77(2):161-174.

[14] SOLLERO P, ALIABADI M H. Fracture mechanics analysis of anisotropic plates by the boundary element method[J]. International Journal of Fracture, 1993,64(4):269-284.

[15] KE C C, CHEN C S, TU C H. Determination of fracture toughness of anisotropic rocks by boundary element method[J]. Rock Mechanics and Rock Engineering, 2008,41(4):509-538.

[16] ADACHI J I, DETOURNAY E. Plane strain propagation of a hydraulic fracture in a permeable rock[J]. Engineering Fracture Mechanics, 2008,75(16):4666-4694.

[17] SIH G C, PARIS P C, IRWIN G R. On cracks in rectilinearly anisotropic bodies[J]. International Journal of Fracture Mechanics, 2015,47(1):189-203.

[18] BOUHALA L, MAKRADI A, BELOUETTAR S. Thermo-anisotropic crack propagation by XFEM[J]. International Journal of Mechanical Sciences, 2015,103:235-246.

[19] HU K, CHEN Z. Size effect on crack kinking in a piezoelectric strip under impact loading[J]. Mechanics of Materials, 2013,61:60-72.

[20] HWU C. A unified definition of stress intensity factors for cracks/corners/interface cracks/interface corners in anisotropic/piezoelectric/viscoelastic materials [J]. Procedia Materials Science, 2014,3(3):257-263.

[21] 李世愚.岩石断裂力学导论[M].合肥:中国科学技术大学出版社,2010.

[22] HUESO J L, MARTNEZ E, TORREGROSA J R. Modified Newtons method for systems of nonlinear equations with singular Jacobian[J]. Journal of Computational and Applied Mathematics, 2009,224(1):77-83.

(编辑 李志芬)

Numerical simulation of hydraulic deep jet perforation on fracture propagation and orientation

ZHONG Guanyu, WANG Ruihe, ZHOU Weidong, CHEN Guichun, WAN Chunhao

(SchoolofPetroleumEngineeringinChinaUniversityofPetroleum,Qingdao266580,China)

A fracture propagation model in the process of deep jet perforation was established based on the anisotropic elasticity theory and the principles of fluid mechanics in porous media, and a method for determining the propagation angle of the fractures was proposed referring to the maximum hoop stress theory. A Newton method was used to solve the numerical model, which has been verified by case studies. The results show that the radius of the reoriented fractures increases with the increase of the jet perforation length and jet angle, and it also increases with the increase of the pumping rate and viscosity of the fracturing fluid. Symmetric jet perforation is better than the perforation in one side. The fracture reorientation radius increases with the anisotropic ratio and the elastic modules, while it decreases with the increase of the stress difference.

hydraulic deep jet perforation; hydraulic fracture; fracture propagation morphology; elastic module; anisotropic

2016-02-29

国家“973”项目(2014CB239202)

仲冠宇(1987-)，男，博士研究生，研究方向为岩石力学、水射流和水力压裂。E-mail：zhongguanyu0606@163.com。

1673-5005(2016)05-0079-08

10.3969/j.issn.1673-5005.2016.05.009

F 407.22

:A

仲冠宇,王瑞和,周卫东,等. 水力深穿透射孔对压裂裂缝形态影响的数值模拟[J].中国石油大学学报(自然科学版),2016,40(5):79-86.

ZHONG Guanyu, WANG Ruihe, ZHOU Weidong, et al. Numerical simulation of hydraulic deep jet perforation on fracture propagation and orientation[J].Journal of China University of Petroleum(Edition of Natural Science),2016,40(5):79-86.