一基于GA-BP神经网络的ACFM实时高精度裂纹反演算法

李 伟, 袁新安, 曲 萌, 陈国明, 葛玖浩, 孔庆晓, 张雨田, 吴衍运

(中国石油大学海洋油气装备与安全技术研究中心,山东青岛 266580)



一基于GA-BP神经网络的ACFM实时高精度裂纹反演算法

李 伟, 袁新安, 曲 萌, 陈国明, 葛玖浩, 孔庆晓, 张雨田, 吴衍运

(中国石油大学海洋油气装备与安全技术研究中心,山东青岛 266580)

针对传统交流电磁场检测(ACFM)特征信号难以实现缺陷高精度实时反演的问题,在电磁耦合ACFM探头有限元模型分析的基础上,引入能量谱和相位阈值判定方法实时获取裂纹特征信号,建立裂纹实时反演实验系统并进行裂纹检测实验,基于加入遗传算法的BP神经网络(GA-BP)建立的ACFM实时高精度裂纹反演算法对实验得到的裂纹特征信号进行长度和深度的反演。结果表明:电磁耦合ACFM探头有限元模型可较好地仿真裂纹特征信号;采用能量谱和相位阈值判定方法能够实时获取裂纹特征信号;GA-BP神经网络能够实现裂纹长度和深度的反演,反演精度误差不超过10%。

ACFM; 实时; 高精度; 裂纹反演算法; 遗传算法; BP神经网络

交流电磁场检测(ACFM)技术最早应用于海洋钻井平台焊缝检测,由于非接触测量、无须标定、提离效应小、数学模型精确等特点,已经广泛应用于石油化工、铁路运输、核能等领域[1-3]。ACFM技术利用激励线圈在工件表面感应出匀强电流场,当电流垂直穿过缺陷时,电流会从缺陷两端和底部绕过,引起周围空间磁场发生畸变。X方向磁通密度产生波谷,波谷深度可反映缺陷深度。Z方向磁通密度产生波峰和波谷,峰谷之间距离可反映缺陷长度[4-5]。在无损检测领域中,由缺陷得到特征信号称之为正演模型,反之,由特征信号得到缺陷形状,称之为反演模型[6]。通常由缺陷得到特征信号容易实现,由特征信号反演缺陷形状较为复杂,但缺陷形状信息能够反映结构的破坏程度,是结构评估十分关心的问题[7]。ACFM技术数学模型精确,其特征信号Bz反映裂纹长度信息,Bx包含裂纹深度信息,具有良好的缺陷剖面(长度和深度)反演条件。传统ACFM插值反演算法相对简单,但精度低且实时性差[8-9];利用特征信号的反演算法,对样本数据库有较高的要求,特征信号之间的相互影响造成反演过程复杂,必须完成缺陷扫描后进行特征信号分析或蝶形图判定,难以实现实时判定和反演[10]。针对这些问题,笔者建立ACFM探头电磁耦合仿真模型,通过能量谱和相位阈值判定方法实时获取裂纹反演特征信号样本数据库,引入反向传播(BP)神经网络和遗传算法(GA)实现ACFM裂纹长度和深度的高精度反演。

1 电磁耦合ACFM探头仿真模型

选择ANSYS中的三维电路耦合绞线圈CIRCU124,根据需要设置其选项使其成为电源,将其K节点与探头模型需要结合的位置上的节点用E命令生成一个耦合单元。由于绞线圈中的电流和通过线圈终端的电势降是唯一的,所以将线圈每匝电流(CURR)自由度和通过线圈终端的电势降(EMF)自由度分别耦合在一起。建立如图1所示的三维ACFM探头电磁耦合运动仿真模型。

模型中激励探头为U型载流线圈[11-12],线圈下方设有提取感应磁场电压的X线圈(提取X方向磁场的感应电压)和Z线圈(提取Z方向磁场的感应电压)。仿真模型中裂纹长15 mm,宽0.8 mm,深5 mm,加载激励电压为1 V,频率为6 kHz,检测线圈提离高度为2 mm。选择谐波求解器,沿着裂纹上方建立一条路径,分别提取路径上方X、Z方向线圈内的电压值Ex和Ez,如图2所示。

图1 电磁耦合ACFM探头仿真模型

图2 裂纹特征信号仿真结果

特征信号Ex在非裂纹区保持一定数值,当进入裂纹区(14～29 mm)后X方向磁通密度减小导致Ex出现波谷。由于提取的感应电动势均为正值,因此Ez在未进入裂纹区基本为0,在裂纹两端(14 mm和29 mm)聚集区出现两个峰值。Ex和Ez规律与ACFM原理一致,验证所建立的电磁耦合ACFM探头仿真模型的正确性。

2 缺陷特征信号实时判定方法

传统ACFM技术常采用特征识别方法,即根据Ex和Ez的特征或者由Ex和Ez组成的蝶形图来判别[13]。由于基于特征信号或蝶形图的判别方法需要在探头完全扫过裂纹后依据获取信号的特征进行判别,难以实现缺陷特征信号的实时数据存储与处理。采用能量谱和相位阈值判别方法,可依据阈值实时保存缺陷有效信号特征值,为缺陷的实时、高精度反演奠定基础。

如图2所示,由于Ex的峰值之间距离(16 mm)大于Ez峰峰距离(14 mm),也大于裂纹长度(15 mm),因此Ex包含更多缺陷信息(深度及长度,特别是长度估算有安全余量)。

将X线圈的电动势Ex通过傅里叶变换的平方换算得能量谱(QEx),如图3所示。在Ex的峰峰间距内(虚线范围),取能量谱QEx的最大值Q,以Q数值画一条水平线,该水平线与Ex能量谱的交点位置(实线区域)明显大于Ex峰值,则位于Q以下的能量谱信息包含裂纹全部长度和深度信息。选定Ex能量谱的峰值Q作为裂纹实时判定的阈值。

图3 Ex能量谱曲线

由于裂纹区两侧Z方向的磁通密度相反,当检测线圈进入缺陷时Ez的相位会发生变化,如图4所示。在裂纹区(14～29 mm)处,Ez的相位有突变，Ez相位导数在裂纹区域出现明显的峰值。选定Ez相位的导数作为裂纹实时判定的另一依据。依据Ex能量谱和Ez相位阈值实时判定方法能够实时获取裂纹特征信号,所设计裂纹特征信号实时判定法如图5所示。主要步骤如下:

(1)对采集到的Ex、Ez和激励信号进行锁相放大和数据处理,得到Ex能量谱QEx和Ez相位φZ。

图4 Ez相位变化关系

图5 缺陷特征信号实时判定方法

(2)判断QEx与阈值大小关系。若QEx小于等于Q,则保存数据。若QEx大于Q,则舍弃该数据。

(3)对Ez相位求导得到Dz。判断Dz是否满足要求(本文中相位判断设有余量,Ez相位导数阈值设为180)。Dz大于等于180则视为有效数据,将保存的数据作为缺陷特征信号样本数据库;若Dz小于180则递增阈值Q并清空保存的缺陷数据,并继续进行阈值判定。

该算法实时更新阈值可有效避免裂纹特征信号的误判,可在检测线圈进入裂纹区时及时有效保存裂纹特征信号,无须完全扫过裂纹进行缺陷的判断,达到裂纹实时判定的目的。

3 裂纹实时反演实验

3.1 检测系统设计

依据ACFM技术原理,设计裂纹实时反演实验系统,如图6所示。ACFM激励探头选用U型载流线圈,利用直径为0.5 mm的漆包线在锰锌铁氧体磁芯横梁上缠绕500圈。检测线圈采用线圈式传感器,利用直径为0.15 mm的漆包线在矩形小磁芯上缠绕两个方向相互垂直的小线圈,分别用于拾取X方向磁通密度Bx和Z方向磁通密度Bz。

图6 裂纹实时反演ACFM检测系统设计

信号发生器产生幅值为1 V,频率为6 kHz的正弦激励信号,经过功率放大输送给激励线圈。激励线圈在试件表面产生均匀激励电流区域,电流经过缺陷引起空间磁场畸变。检测线圈拾取Bx和Bz信息并转化为电信号Ex和Ez。Ex和Ez经过调理电路(放大和滤波),由采集系统传输至计算机。计算机内部基于Ex能量谱和Ez相位阈值缺陷特征信号实时判定软件可实时获取缺陷特征信号。最终搭建的裂纹实时反演检测系统实物如图6所示。

试件为低碳钢板,钢板上采用电火花技术刻有不同尺寸的矩形人工裂纹。利用PLC控制扫描台架带动ACFM探头(激励和检测线圈)沿着其中一条裂纹(长40 mm,深6 mm)进行匀速扫描,扫描速度为3 mm/s,测控软件采集Ex、Ez和探头的位置信息,得到的缺陷特征信号如图7所示。

为了实现缺陷的实时、高精度反演量化,引入灵敏度作为缺陷尺寸反演的特征量[14]:

式中,Ex0为远离裂纹处Ex分量信号幅值;Exmin为Ex信号幅值最小值;Ezmax为Ez信号畸变最大幅值。

图7 裂纹检测特征信号

对获取的裂纹特征信号进行实时分析,得到Ex灵敏度Sx为9.2%,Ez灵敏度Sz为26.63%,Ez峰值之间距离Lz为38.46 mm。同时,对不同深度和长度裂纹进行检测,得到不同裂纹尺寸的信号特征量如表1所示。

3.2 基于GA-BP的缺陷反演算法

如图8所示,利用MATLAB中的newff函数创建4层BP神经网络,默认缺省initnw初始化权重与偏置[15]。initnw方法虽然使得每层神经元的活动区域能大致平坦地分布在输入空间,但是由此训练所得的网络存在网络结构不确定问题,即初始权重与偏置的取值是随机的。由此可见,BP算法存在收敛速度慢、不能保证收敛到全局最小点、网络结构不易确定等特点[16]。

遗传算法具有很好的收敛性和鲁棒性,在较高计算精度时,计算时间少[17-18]。在BP网络训练之前增加一步遗传算法优化神经网络的权重和偏置(GA-BP神经网络模型),以便确定一组最优的初始化权重与偏置,从而优化BP人工神经网络的结构[19-21]。

表1 不同尺寸裂纹特征信号数据库

图8 4层BP神经网络模型

在缺陷反演GA-BP神经网络中,输入向量包括Ex灵敏度和Ez灵敏度以及Ez分量波形峰谷间距3个特征量,输出向量为缺陷长度和深度两个特征量,由此建立的4层BP网络模型的神经元矩阵为[5,6,2]。以表1中的1～16组作为训练样本,17～19组作为测试样本。由于缺陷尺寸取值范围也有较大差异,为了提高预测精度,需要在训练前对表1中的样本数据进行[-1,1]区间内的归一化处理。遗传算法求解BP神经网络权重和偏置过程如图9(a)所示,BP神经网络训练过程如图9(b)所示。

对建立的GA-BP神经网络进行学习,并对样本数据库内的第17组裂纹(长43 mm,深 5 mm)进行样本预测,得到裂纹预测结果如图10所示。反演结果显示第17组裂纹尺寸:长度为40.70 mm,深度为4.72 mm,长度误差为5.35%,深度误差为5.60%。

同样地利用GA-BP神经网络对18组和19组样本裂纹进行反演,反演结果见表2。

图9 GA-BP神经网络模型训练过程

图10 GA-BP网络对第17组裂纹反演结果

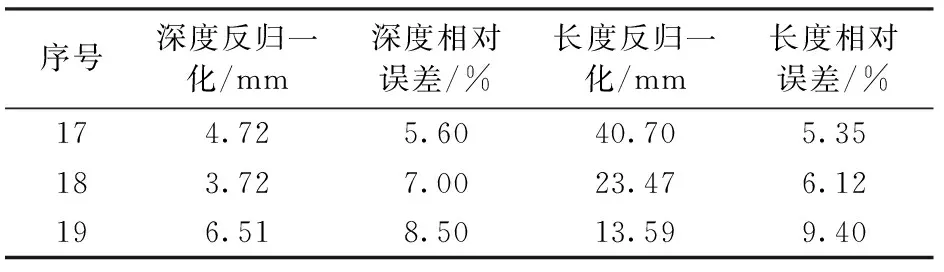
表2 基于GA-BP神经网络的测试样本预测结果

第18、19组样本裂纹长度反演误差分别为6.12%和9.40%,深度反演误差分别为7.00%和8.50%。由表2可以看出,基于GA-BP神经网络对于较浅裂纹、较长裂纹具有更好的预测能力。与裂纹实际尺寸相比,基于GA-BP神经网络预测裂纹尺寸相对误差不超过10%,满足工程实际要求。

4 结论

(1)建立的电磁耦合ACFM仿真模型能够准确获取裂纹上方X线圈和Z线圈内部的电压Ex和Ez。

(2)基于Ex能量谱和Ez相位导数的阈值判定方法可实时获取裂纹特征信号。

(3)基于GA-BP神经网络的裂纹反演算法可有效地预测缺陷长度和深度,预测误差不超过10%,满足工程实际要求。

[1] LUGG M C. The first 20 years of the A.C. field measurementtechnique:18th World Conference on Non-Destructive Testing (WCNDT)[C]. South Africa,2012:16-20.

[2] 李伟,袁新安,陈国明,等.基于外穿式交流电磁场检测的钻杆轴向裂纹在役检测技术研究[J].机械工程学报,2015,51(12):8-15. LI Wei, YUAN Xinan, CHEN Guoming, et al. Research on in-service detection for axial cracks on drill pipe using the feed-through alternating current field measurement [J].Journal of Mechanical Engineering, 2015,51(12):8-15.

[3] NICHOLSON G L, DAVIS C L. Modelling of the response of an ACFM sensor to rail and rail wheel RCF cracks [J]. NDT & E International, 2012,46:107-114.

[4] LI W, YUAN X A, CHEN G M, et al. A feed-through ACFM probe with sensor array for pipe stringcracks inspection [J]. NDT & E International, 2014,67:17-23.

[5] 齐玉良,陈国明,张彦廷. 交流电磁场检测数值仿真及其信号敏感性分析[J]. 石油大学学报(自然科学版),2004,28(3):65-68. QI Yuliang, CHEN Guoming, ZHANG Yanting. Numerical simulation on alternating current field measurement and sensitivity analysis of detected signal [J].Journal of the University of Petroleum, China (Edition of Natural Science),2004,28(3):65-68.

[6] RAMUHALLIP, UDPA L, UDPA S S. Electromagnetic NDE signal inversion by function-approximation neural networks [J]. IEEE Transactions on Magnetics, 2002,38(6):3633-3642.

[7] MAAZI M, BENZAIM O, GLAY D, et al. Detection and characterization of buried macroscopic cracks inside dielectric materials by microwave techniques and artificial neural networks [J]. IEEE Transactions on Instrumentation and Measurement, 2008,57(12):2819-2816.

[8] 李伟.基于交流电磁场的缺陷智能可视化检测技术研究[D].青岛:中国石油大学,2007. LI Wei. Research on ACFM based defect intelligent recognition and visualization technique [D].Qingdao: China University of Petroleum, 2007.

[9] 李伟,陈国明.基于双U形激励的交流电磁场检测缺陷可视化技术[J].机械工程学报,2009,45(9):233-237. LI Wei, CHEN Guoming. Defect visualization for alternating current field measurement based on the double U-shape inducer array [J]. Journal of Mechanical Engineering, 2009,45(9):233-237.

[10] NOROOZI A, HASANZADEH R P R, RAVAN M. A fuzzy learning approach for identification of arbitrary crack profiles using ACFM technique [J]. IEEE Transactions on Magnetics, 2013,49(9):5016-5027.

[11] LI W, CHEN G M, YIN X K, et al. Analysis of the lift-off effect of a U-shaped ACFM system [J].NDT & E International, 2013,53:31-35.

[12] LI W, CHEN G M, LI W Y, et al. Analysis of the inducing frequency of a U-shaped ACFM system [J].NDT & E International, 2011,44:324-328.

[13] LUGG M, TOPP D. Recent developments and applications of the ACFM inspection method and ACSM stress measurement method:proceedings of ECNDT,2006 [C].Berlin:Germany, c2006.

[14] NICHOLSON G L, KOSTRYZHEV A G, HAO X J, et al. Modelling and experimental measurements of idealized and light-moderate RCF cracks in rails using an ACFM sensor [J]. NDT & E International, 2011,44:427-437.

[15] 李萍,曾令可,税安泽,等.基于MATLAB的BP神经网络预测系统的设计[J].计算机应用与软件,2008,25(4):149-150. LI Ping, ZENG Lingke, SHUI Anze, et al. Design of forecast system of back propagation neural networks based on MATLAB [J].Computer Applications and Software, 2008,25(4):149-150.

[16] 李伟,陈国明,郑贤斌. 基于广义回归神经网络的交流电磁场检测裂纹量化研究[J]. 中国石油大学学报(自然科学版), 2007,31(2):105-109. LI Wei, CHEN Guoming, ZHENG Xianbin. Crack sizing for alternating current field measurement based on GRNN [J].Journal of China University of Petroleum (Edition of Natural Science), 2007,31(2):105-109.

[17] 崔挺,孙元章,徐箭,等.基于改进小生境遗传算法的电力系统无功优化[J].中国电机工程学报,2011,31(19):43-50. CUI Ting, SUN Yuanzhang, XU Jian, et al. Reactive power optimization of power system based on improved niche genetic algorithm[J]. Proceedings of the CSEE,2011,31(19):43-50.

[18] 杨国军,崔平远,李琳琳.遗传算法在神经网络控制中的应用与实现[J].系统仿真学报,2001,13(5):567-570. YANG Guojun, CUI Pingyuan, LI Linlin. Applying and realizing of genetic algorithm in neural networks control [J]. Journal of System Simulation, 2001,13(5):567-570.

[19] 李伟超,宋大猛,陈斌.基于遗传算法的人工神经网络[J].计算机工程与设计,2006,27(2):316-318. LI Weichao, SONG Dameng, CHEN Bin. Artificial neural network based on genetic algorithm [J]. Computer Engineering and Design, 2006,27(2):316-318.

[20] 李松,刘力军,解永乐.遗传算法优化BP神经网络的短时交通流混沌预测[J].控制与决策,2011,26(10):1581-1585. LI Song, LIU Lijun, XIE Yongle. Chaotic prediction for short-term traffic flow of optimized BP neural network based on genetic algorithm [J]. Control and Decision, 2011,26(10):1581-1585.

[21] 李松,罗勇,张铭锐.遗传算法优化BP神经网络的混沌时间序列预测[J].计算机工程与应用,2011,47(29):52-55. LI Song, LUO Yong, ZHANG Mingrui. Prediction method for chaotic time series of optimized BP neural network based on genetic algorithm [J].Computer Engineering and Applications,2011,47(29):52-55.

(编辑 沈玉英)

Real-time and high-precision cracks inversion algorithm for ACFM based on GA-BP neural network

LI Wei, YUAN Xinan, QU Meng, CHEN Guoming, GE Jiuhao,KONG Qingxiao, ZHANG Yutian, WU Yanyun

(CenterforOffshoreEquipmentandSafetyTechnologyinChinaUniversityofPetroleum,Qingdao266580,China)

It is hard to achieve a real-time and high-precision cracks inversion for alternating current field measurement(ACFM) based on traditional characteristic signals. In this paper, based on the finite element method (FEM) model of electromagnetic coupling ACFM probe, the energy spectrum and phase threshold determination methods were presented to obtain the crack characteristic signals in real time. The real-time and high-precision cracks inversion system for ACFM was set up and verified by artificial cracks experiment. The length and depth of cracks were calculated using the characteristic signals obtained from experiments based on the genetic algorithm and back propagation neural network(GA-BP) real-time and high-precision cracks inversion algorithm. The results show that the FEM model of electromagnetic coupling ACFM probe can simulate the characteristic signals perfectively, the energy spectrum and phase threshold determination method can obtain the crack characteristic signals in real time, the GA-BP neural network can realize the inversion of the length and depth of crack perfectly and the relative error of inversion accuracy is less than 10%.

alternating current field measurement(ACFM); real-time; high-precision; cracks inversion algorithm; genetic algorithm;BP neural network

2015-11-20

国家自然科学基金项目(51574276)；中央高校基本科研业务费专项(15CX05024A)；山东省自然科学基金英才基金项目(ZR2015EM009)；青岛市科技成果转化引导计划(青年专项)(14-2-4-49-jch)；中国石油大学(华东)研究生创新工程(YCX2015039)

李伟(1980-)，男，副教授，博士，研究方向为海洋油气设备安全检测技术、传感器设计及其系统仿真。E-mail：liwei@upc.edu.cn。

袁新安(1990-)，男，博士研究生，研究方向为交流电磁场检测技术和油气管道无损检测技术。E-mail：xinancom@163.com。

1673-5005(2016)05-0128-07

10.3969/j.issn.1673-5005.2016.05.016

O 346.1

:A

李伟, 袁新安,曲萌,等.基于GA-BP神经网络的ACFM实时高精度裂纹反演算法[J]. 中国石油大学学报(自然科学版), 2016,40(5):128-134.