基于OpenCL的ICP点云并行配准算法

刘 忠 建

(北方工业大学计算机学院 北京 100144)



基于OpenCL的ICP点云并行配准算法

刘 忠 建

(北方工业大学计算机学院 北京 100144)

针对当前点云配准算法效率过低的问题，运用OpenCL实现了基于通用GPU的kd-tree并行搜索算法，进而实现了ICP点云并行配准算法。首先建立目标点云的三维空间kd-tree，并使用OpenCL并行加速其搜索算法；然后将并行加速的kd-tree搜索算法运用于ICP算法，同时针对ICP算法的其他部分也使用OpenCL并行加速以确保配准过程尽可能高效。通过实验验证了所实现算法的高效性以及健壮性。

OpenCL GPU kd-tree 点云配准 ICP

0 引 言

随着三维扫描技术的发展成熟与普及，三维应用技术得到了较好的发展。特别是在逆向工程、缺陷检测、文物保护、医学手术、3D打印以及游戏娱乐等领域获得了广泛的关注与研究。由于部分遮挡等问题，所以为了获得完整的点云数据，需要进行多次扫描拼接配准。而三维点云配准一直以来都是三维扫描问题中的关键技术。

随着三维扫描器材设备的不断发展更新，扫描数据量不断增大，传统的配准算法随着数据量的激增效率逐渐降低，无法满足实时性的需求。图形处理单元GPU、开放运算语言OpenCL以及计算机视觉与计算机图形学的发展为解决相关大数据量的问题提供了通用的、高性能的并行计算环境，使得实时解决点云配准问题成为可能。本文基于OpenCL对kd-tree搜索算法并行加速，实现了高效并行的ICP[1]配准算法，对于提高配准算法的效率具有十分显著的效果。

1 相关工作

点云配准算法通常是指ICP点云配准算法，该算法是通过迭代点云数据X={x1,x2,…,xnx}和Y={y1,y2,…,yny}反复迭代计算旋转矩阵R与平移向量t，使得对应点的距离和最小，即通过下面的目标函数最小化实现点云的配准工作。

(1)

已有围绕ICP配准算法做出的很多研究与改进，其中Zhang[2]提出引入kd-tree算法对搜寻对应点起到了很好的加速作用。Granger等[3]提出将最大期望算法EM(Expectation Maximization algorithm)算法应用到ICP中，较好地解决了ICP配准算法初始配准的问题。Rusinkiewicz等[4]对有关ICP配准算法所做的改进作了一个全面的分析与总结。Gold等人[5]提出了一种名为Softassign的配准算法，具有较好的配准效果。但是EM-ICP算法与Softassign算法由于算法本身的原因需要计算两个点云数量相乘的矩阵，使得算法在点云数量集不断增大的情况下，可行性与实时性急速降低。Tamaki等人[6]使用了CUDA(compute unified device architecture)对EM-ICP配准算法以及Softassign配准算法进行了并行优化，但实验所使用的数量级也不能达不到数据量不断增加的需求，并且CUDA目前只支持NVIDIA系列显卡，不能做到对绝大多数CPU、显卡等异构平台的通用性支持。国内针对点云配准的研究也是基于CUDA的EM-ICP与Softassign算法的研究，其中蔡静等人[7,8]采用的是下采样的方法来降低配准数据的数据量。下采样会对原始数据造成分辨率以及细节的缺失，本文认为这种做法是不太可取的。即使是下采样过后，采用这两种算法要求的计算数据量也是相当大的，这也是本文不采用这两个算法的一个重要原因。

2 ICP配准算法

ICP配准算法即迭代最近点配准算法，是一种基于自由形态曲面的配准算法。对于两个待匹配的点云数据集X和Y，在数据点集X中找到一点xi与Y点集中一点yi对应，使目标函数式(1)最小。而EM-ICP配准算法[4]由于引入了最大期望算法，它的目标函数为:

(2)

(3)

其中σp是参数，d0是初始已知值，αij为两点为对应点的概率。同样，Softassign配准算法[5]中引入了双随机矩阵，再运用近似均值优化以及模拟退火算法，其目标函数为：

(4)

因此EM-ICP与Softassign算法所计算的数据量为nx×ny，而ICP所需要计算的数据量为ny。

ICP配准算法如下：

输入待配准点云数据X={x1,x2,…,xnx}和Y={y1,y2,…,yny}、R0、t0；

输出配准结果R′和t′。

步骤1R0←I，t0←0；

步骤2for k=1，…，maxIterations do;

步骤3for each point yiin Y do;

步骤4寻找到最近的点xikin X：

步骤5end for;

步骤6建立对应于Y的Xk={x1k,x2k,…,xnyk}数据集;

步骤7利用四元数计算R′和t′;

步骤8Rk←R′，tk←t′;

步骤9end for。

有些研究学者认为ICP算法的关键问题不在于它的配准速度而在于其配准的精度，即ICP一直存在的初始位置的问题。当两个点云的初始位置距离很远或者重叠部分不是特别好时，ICP配准算法的效果是相当差的，这也是很多学者倾向于认为配准点云实际上是一种粗配准(又叫预配准)的原因。另一个角度而言，构建一个模型或者一个空间的扫描建模时，是可以控制相邻点云数据的重叠以及距离的。因此，本文认为ICP算法在做扫描点云配准时还是优于其他配准算法，这也是本文用ICP算法做点云配准的主要原因。

3 kd-tree算法

kd-tree是一种分割k维数据空间的数据结构，主要应用于多维空间关键数据的搜索(如：范围搜索和最近邻搜索)。kd-tree是二进制空间分割树的一种特殊情况。kd-tree由Zhang[2]首先引入到ICP算法中，用于最近邻搜索。kd-tree算法分为两个部分，第一部分为创建kd-tree，第二部分才是本文的目的:搜索最近邻的节点。

创建kd-tree分为递归算法与非递归的算法，为提高效率，本文采用的是非递归算法。而搜索算法也是采用非递归式的搜索，因此本文将搜索算法分为两个步骤，即先向下搜索直到叶子节点，找到第一个最近邻参照节点，随后利用父节点信息对满足条件的节点进行回溯搜索。

4 基于OpenCL的并行算法

开放计算语言OpenCL是一个为异构平台编写程序的框架，此异构平台可由CPU、GPU或其他类型的多核处理器组成。OpenCL为开发人员提供了基于任务分割和数据分割的并行计算机制以及一套支持C99标准的内核API与控制API，以帮助开发人员在GPU上运行一个并行的内核函数，充分提高算法运行效率。

4.1 GPU下的kd-tree算法

kd-tree的数据结构大大地方便了单个数据在k维空间中进行搜索，但是当需要搜索的数据量非常大时，kd-tree的搜索还是会比较迟缓的。因此，为了进一步提高算法的效率，将kd-tree算法运用OpenCL移植到GPU上，通过并行对多个数据同时进行搜索来达到提高算法效率的目的。

为方便地将kd-tree的节点数据传输到GPU下，使用一个数组的形式来存储kd-tree的节点，将当前节点的子节点用一个整型数组来存储它们的序号，以方便查找。同样为了方便回溯查找可能的最近邻节点，设置一个整型数据位表示父节点的序号。采用数组结构存储kd-tree的节点主要是考虑到满足GPU下全局内存的管理。对于GPU下建立kd-tree，本文方法会比直接使用CPU下的kd-tree繁琐一点。首先，利用输入的样本集在CPU下建立kd-tree；然后将CPU下的kd-tree节点转换为GPU下所支持的数组存储形式；最后将kd-tree传输到GPU的全局内存中，用于搜索使用。下面主要介绍GPU下的最近邻搜索算法。

本文所使用的kd-tree搜索算法分为三个步骤：第一步，从根节点向下根据kd-tree特性采用二分搜索；第二步，逐个比较叶子节点中所包含的样本数据集，选取最近邻节点；第三步，如果分支节点与待查询节点距离小于第二步中得到的最近邻节点与待查询节点距离，采用回溯查找的策略以确定最近邻节点，否则返回第二步中的结果。

GPU下的kd-tree最近邻搜索算法如下：

输入将kd-tree、点云数据集X和Y加载到GPU的全局内存；

输出对应点点集与对应点点集所对应的欧氏距离。

步骤1分配n个线程，n为查询的点集数量；

步骤2在GPU中为输出分配相应的存储空间；

步骤3对每一个线程并行执行kd-tree搜索程序：

(1) 如果kd-tree是空的，则设距离为无穷大并返回；

(2) 沿kd-tree树向下搜索直到叶子结点；

(3) 如果分支节点与待查询节点的距离小于步骤(2)中搜索到的最近邻节点与待查询节点的距离，则回溯搜索，以确定最近邻节点；否则返回步骤(2)中的查询结果。

步骤4将GPU内存中的结果拷贝到内存中。

在实验中，发现了两个问题：第一个是当数据量较大的时候，树的深度在一定程度上影响着搜索算法的效率。根据实验，本文将树的最大深度定在13层会取得较好的结果，然后对叶节点中所包含的样本数据集再采用逐个比较的方式选取最近邻节点。第二个问题则是回溯算法的必要性问题。首先ICP算法本身就是一种采用最近邻近似寻求对应节点以解决配准问题的一个算法。其次，kd-tree按照二维划分所找到的近似最近邻节点与真实最近邻节点的差距十分小。回溯算法需要更新最近邻节点的可能性也不是特别高。按照以上分析，本文做了关于回溯算法必要性以及回溯栈大小的影响的实验。本文将在第5节给出实验结果。

4.2 GPU下的ICP算法

原始的ICP算法主要包括三大步骤：第一步是利用最近邻搜索查找对应点；第二步是利用四元数估计变换矩阵；第三步是通过变换矩阵转换数据。当目标方程达到误差标准时，退出算法，否则转到第一步继续执行。这三个步骤构成了ICP算法的基本结构，除第一步的对应点搜索外，其他两步包含大量的矩阵操作。第二步包含两个点云的交叉协方差矩阵与重心的计算都可以使用GPU加速。此外，第三步数据的转换其实就是两个矩阵相乘，因此也可以运用GPU加速，以提高算法的效率。

Bouaziz等人[9]提出了一种新的衡量ICP算法的目标方程，称作lp-ICP。即式(1)可改为：

(5)

该算法在文献[9]中得到证实，当p∈[0,1]的区间内时，可以有效地减少错误的对应点以及噪声点对算法的影响，以提高ICP算法配准的精度。但由于该文献采用了一种优化算法，迭代优化次数比较多，算法的执行时间比较长。本文简单地将这个方法使用在原始的ICP算法中用来排除错误对应点以及噪声点的影响，提高配准的精度。

5 实验结果及分析

本文将通过三个不同实验设计来验证本文所实现的算法，分别验证本文算法的运行效率与配准的精度。实验的编译环境为：Ubuntu 12.04 64位。实验的硬件环境为：CPU为i7-4770处理器，主频3.40 GHz；GPU为AMD HD8490显卡，显存为1 GB，位宽为64位，主频为875 MHz，流处理器160个，该显卡属于低端显卡。NVIDIA显卡只需一个流处理器就能发挥作用，而AMD的显卡对流处理器定位不一样，要5个流处理器单元一组才能工作。实验所用数据为Kinect拍摄的室内场景。实验数据以及效果如图1和图2所示。

图1 拍摄数据实验效果

图2 斯坦福兔子实验效果

5.1 基于OpenCL下的ICP与CPU下的ICP比较

将本文的算法与未使用OpenCL加速的情况下以及Open PCL(Open Point Cloud Library)中所实现的ICP算法进行了运行效率对比，本文改进后算法具有较好的效率，特别是使用OpenCL并行加速之后的算法，效率有了较大的提升。实验结果如图3所示。

PCL-ICP为PCL库中的ICP算法，KDtree-ICP为本文优化之后使用kd-tree所实现的ICP算法，OpenCL-ICP为本文最后实现的基于OpenCL的ICP算法。由于本文尽可能简化、优化kd-tree算法，使得该算法更适用于ICP算法，从实验结果中可以明显发现改进之后的算法在相同的实验环境下比PCL库中所实现的算法有了较好的提高。而从实验中可以明显看到使用OpenCL之后的算法的执行效率有了较大的提升，但由于GPU计算核心的限制，在数据量较大时，算法的效率还是不够理想。如果采用性能更好的显卡，可以获得更好的结果。

5.2 回溯栈的大小对算法的影响

本文在实验中发现回溯栈的大小对算法具有较大的影响。首先从ICP算法本身考虑，ICP算法本身就是通过最近邻节点近似表示对应点，通过kd-tree进行筛选之后的节点对于搜索点已经是一个十分近似的最近邻节点，理论上足以用来表示近似最近邻节点。再从kd-tree的构造上来看，本文并不是将kd-tree一直划分到只剩下一个节点，而是将树建到一定的深度就不再往下继续划分子树。因此每个叶子节点中包含有多个数据节点，在搜索过程中当搜索到叶子节点时是采用逐一比较的方法确定最近节点，这样就再一次从概率的角度缩小了需要再次回溯找到最近邻节点的概率。实验所用数据量为298 227，实验结果如图4所示。

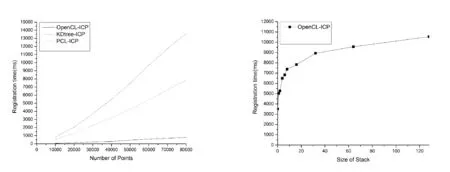
图3 算法效率的实验 图4 回溯栈大小对算法的影响

在实验中发现，随着回溯栈的增大，算法的效率会逐渐降低，但是会有一个最高点；而算法配准的精度当回溯栈大于1之后就没有太大的变化。这样就刚好验证了本文之前的假设：kd-tree算法需要回溯更新最近邻节点的概率比较小，或者说大部分的回溯都是无用的，抑或回溯一次与第一次找到的最近邻节点已经足以表示近似最近邻节点。

5.3 lp-ICP目标函数的影响

根据Bouaziz等人[9]的方法，为了使算法简单，本文只使用了文献[9]中所使用的目标函数来替代本文中使用的目标函数进行实验。可能由于实验中并没有使用该文献所采用的优化算法，算法配准精度的提升并不明显，但是随着实验所取p值的减小，算法的配准精度整体是提高的。

6 结 语

点云配准一直都影响着逆向工程、扫描建模以及模式识别等重要领域。本文根据实验以及算法特性优化kd-tree算法，以使其更适用于ICP点云配准算法。并使用OpenCL平台，运用通用的GPU并行加速技术，实现并行ICP点云配准算法，在一定程度上提高了算法的执行效率，在实际应用中具有一定的价值。传统ICP算法由于采用最近邻查找对应点的算法特性，使得该算法很容易陷入局部最优而导致错误的配准结果。但本文并没有考虑这一影响，所以接下来的工作是如何能够较好地对任意输入的待配准数据进行初始配准，使算法在任意输入下都具有较好的健壮性。

[1] Besl P J,Mckay N D.A method for registration of 3-d shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14(2):239-256.

[2] Zhang Z Y.Iterative Point Matching for Registration of Free-From Curves and Surfaces[J].International Journal of Computer Vision,1994,13(2):119-152.

[3] Granger S,Pennec X.Multi-scale EM-ICP:A Fast and Robust Approach for Surface Registration[C]//Proceedings of the 7th European Conference on Computer Vision (ECCV2002),2002:418-432.

[4] Rusinkiewicz S,Levoy M.Efficient Variants of the ICP Algorithm[C]//Proceedings of the 3rd International Conference on 3-D Digital Imaging and Modeling,2001:145-152.

[5] Gold S,Rangarajan A,Lu C P,et al.New algorithms for 2D and 3D point matching: pose estimation and correspondence[J].Pattern Recognition,1998,31(8):1019-1031.

[6] Tamaki T,Abe M,Raytchev B,et al.Softassign and EM-ICP on GPU[C]//Proceedings of the 2010 1st International Conference on Networking and Computing.Washington DC,USA:IEEE Computer Society,2010:179-183.

[7] 蔡静,董琳,孙晓鹏.3D人耳点云配准的并行Softassign算法[J].计算机工程与设计,2013,34(10):3629-3634.

[8] 董琳,何扬.基于EM-ICP的三维人脸简化点云并行配准算法[J].微型机与应用,2013,32(16):38-41.

[9] Bouaziz S,Tagliasacchi A,Pauly M.Sparse Iterative Closest Point[J].Computer Graphics Forum,2013,32(5):113-123.

PARALLEL REGISTRATION ALGORITHM OF ICP POINT CLOUD BASED ON OPENCL

Liu Zhongjian

(CollegeofComputer,NorthChinaUniversityofTechnology,Beijing100144,China)

In view of the problem of too low efficiency the current point cloud registration algorithm has, by using OpenCL we achieved the general GPU-based kd-tree parallel search algorithm, and then realised the parallel ICP point cloud registration algorithm. First we established the three-dimensional kd-tree of target point cloud, and used the OpenCL to parallelly accelerate its search algorithm. Then we applied the parallelly accelerated kd-tree search algorithm in ICP algorithm, at the same time the OpenCL parallel acceleration was also used aimed at the rest part of ICP algorithm to ensure as much as possible the efficient registration process. Experiments verified the efficiency and robustness of the implemented algorithm.

OpenCL GPU kd-tree Point cloud registration ICP

2015-05-16。国家自然科学基金项目(61202229)；北京市自然科学基金项目(4132018)。刘忠建，硕士生，主研领域：计算机图形学。

TP391.41

A

10.3969/j.issn.1000-386x.2016.11.043