QR二维码纠错改进算法

康伟慈，曹 民

(上海理工大学 光电信息与计算机工程学院，上海 200093)



QR二维码纠错改进算法

康伟慈，曹 民

(上海理工大学 光电信息与计算机工程学院，上海 200093)

二维条码与一维条码相比，其无需依赖数据库，存储信息量大，可表达多种多媒体及文字信息，具有纠错能力。针对传统QR码的纠错能力有限，文中提出了将纠错码LDPC码替换RS码生成新的QR码方案，即利用新的纠错技术生成QR码。通过对纠错码LDPC码的编码原理和性能仿真进行研究，与RS码进行仿真对比。实验结果表明，相比原RS纠错码，新纠错码LDPC码的纠错能力有所提高。

QR码；二维码；RS码；LDPC码

二维码是将特定的图形按照一定规律在平面上形成的黑白相间的图形，储藏着所要传达的信息；常见的二维码有QR Code、PDF417、DataMatrix等[1]。QR(Quick Response Code)码是由日本丰田公司Denso Wave于1994年9月研制的一种矩阵二维码符号，其拥有一维码和所有二维码信息容量大、可靠性高、可表示汉字和图像等多种信息[2]。

1 QR二维码

1.1 QR码符号结构

QR码[3]是包括编码区域和功能区域，功能区域不用于数据编码，包括寻像图形、分隔符、定位图形和校正图形[4]。QR码符号共有40个版本[5]，图1为版本7的结构。

A：3模块 B：5模块 C：7模块

图1 QR Code的符号结构(版本7)

1.2 QR码编码

QR码的编码要经过以下步骤：数据分析、数据编码、纠错编码、数据及纠错信息整合、阵列的构造、掩模、添加格式和版本信息。

2 RS码纠错算法

QR码有4个不同的纠错等级，纠错能力最大为30%。

2.1 Reed-Solomon编码原理

RS(Reed-Solomon)[6]码又称里德-所罗门码，是一种纠错能力很强的非二进制BCH码。RS编码运算在有限域中进行。

RS码的多项式为c(x)=m(x)+r(x)，m(x)为信息多项式，r(x)为校验多项式,m(x)=c2tx2t+c2t+1x2t+1+…cn-1xn-1,r(x)=c0+c1x+…c2t-1x2t-1。

若c(x)为一个码字，则它必须是生成多项式g(x)的倍数，且通过除法算法可获得p(x)。c(x)=q(x)g(x),m(x)=q(x)g(x)+p(x)。

2.2 仿真实验

对RS编码理论分析在仿真平台上进行实验比较，实验给出了误比特率BER为参考的性能曲线。实验采用AWGN信道，BPSK调制，仿真软件为Matlab7.1。

图2 RS信噪比和误码率曲线图

由图2可知，RS的误码率随着信噪比的增加而降低，当信噪比相同时，误码率随信息位K的增加而降低。

3 LDPC码编码算法

3.1 LDPC码

LDPC码[7]是一种(n,k)的线性分组码，通过校验矩阵H获得，H的大小为m×n，一列代表码字的一位，一行代表一个校验方程。

上式代表5×10的校验矩阵和对应的校验方程，满足H×cT=0，其中

c=(c1,c2,c3,c4,c5,c6,c7,c8,c9,c10)∈C

当校验矩阵H是满秩时,m=n-k，码率r=(n-m)/n=1-m/n。若H的秩小于m，即m>n-k，码率是r>1-m/n。

构造维数为m×n的校验矩阵H，利用高斯消元法将其转化为

(1)

3.2 LDPC码算法

利用生成矩阵编码方法是最基础的，但这种方法在码长较长的情况下复杂度O(n)2将是严重的制约因素。因此，需要采取新方法使得生成矩阵中含有大量的“1”元素，为此提出了运用近似下三角矩阵的编码算法[8]。

若H为m×n的行满秩矩阵，通过交换行列转化成近似下三角矩阵[9]如图3所示，并保持了矩阵的稀疏性。

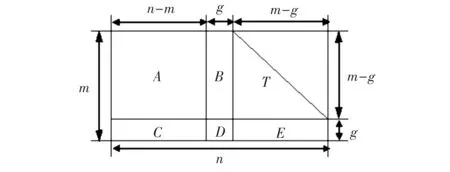
图3 稀疏校验矩阵的近似下三角矩阵

(2)

假设编码码字S=(t,p1,p2)，表示信息比特序列，p1和p2表示校验比特序列。根据HST=0，可得

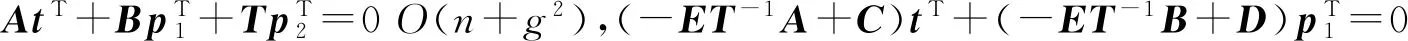
若矩阵(-ET-1B+D)可逆，则可得

(3)

(4)

这种编码算法的复杂度为 。研究主要集中在如何利用校验矩阵的稀疏性来有效的进行编码，目的是使编码的复杂度随着码字长度呈线性增长。

3.3 仿真实验

对LDPC码的编码理论在仿真平台上进行了实验，研究影响LDPC码性能的因素。

图4 LDPC不同迭代次数的性能比较

图4表示的是不同迭代次数对LDPC码性能的影响。由图可知，迭代次数越大，LDPC码的性能越好。

图5 比特错误率与信噪比和迭代次数关系

图5表示了比特错误率与信噪比和迭代次数的关系曲线，由图可知，在信噪比>3dB时，BER快速减小，信噪比比较小时BER变化较慢。

4 LDPC与RS仿真对比

在Matlab实验平台上，以码长512为界限[10]，文中选择信噪比和比特误码率这一对参数进行对比分析，当比特误码率较小时可判断它其纠错性能较好。

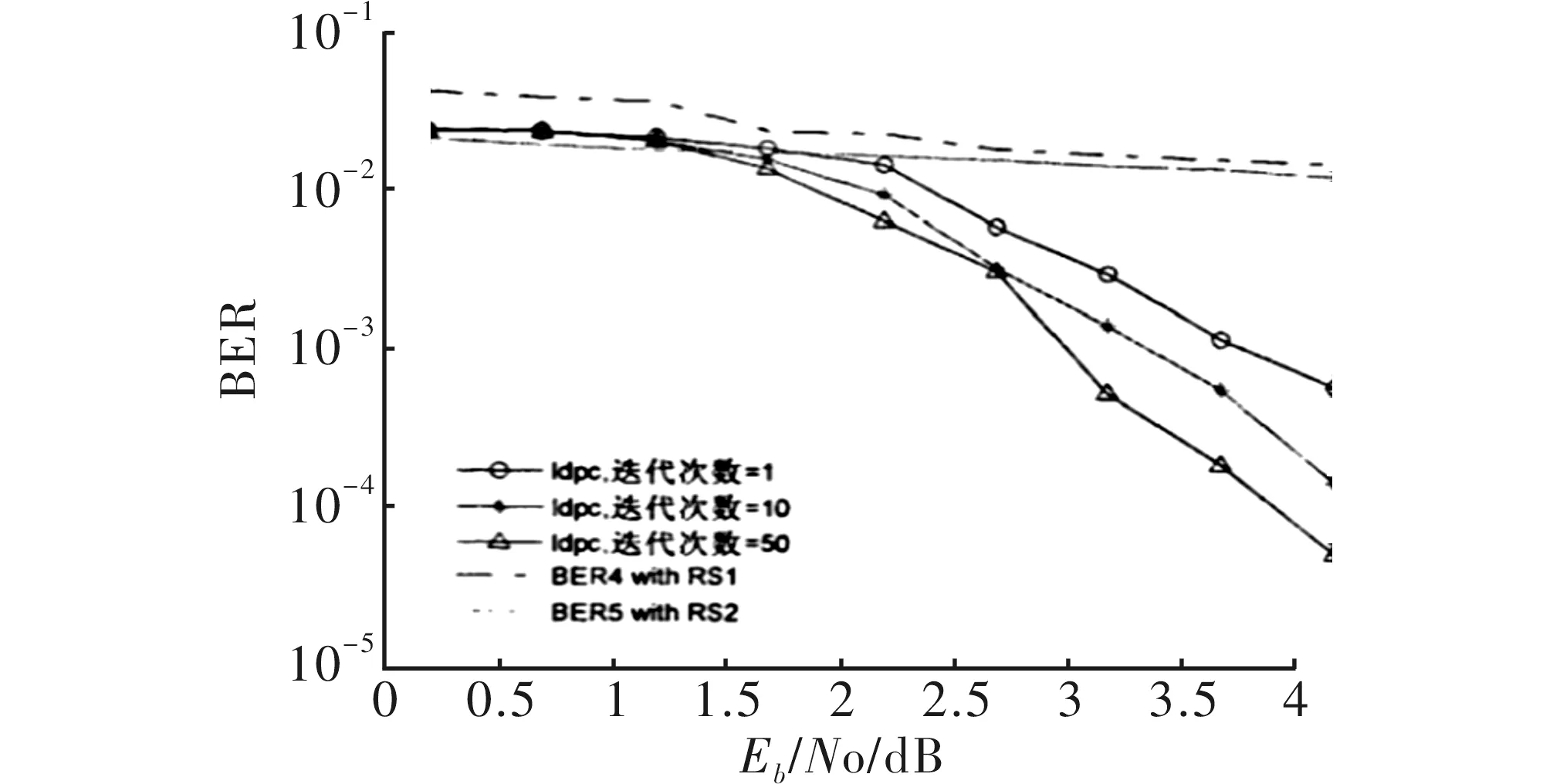
图6 信噪比与比特误码率之间的关系

从仿真结果可以看出，LDPC译码的性能优于RS码，RS码在信躁较低时性能该变量较少，而LDPC码快速降低比特误码率，这样可纠正更多错误。

影响纠错码性能的另一个因素是码率，因此选择在相同码率的情况下进行仿真实验，如图7所示。

图7 LDPC与RS在具有相同码率时的曲线

由图7可知，LDPC码的性能要优于RS，在信噪比较小时LDPC码的误码率就已经降到较低水平，而RS码在信噪比较大时才较为明显。

5 结束语

对LDPC码和RS码的性能进行了分析比较，从仿真结果可知，LDPC码的性能优于RS码。因此使用纠错码LDPC输出新的QR码，提高了纠错能力。

[1] 刘志海,万丽荣,宋作玲.条码技术及程序设计案例[M].北京:化学工业出版社,2009.

[2]LiuYue,LiuMingye.Researchondataencodingoftwo-dimensionalQRcodebarcode[J].JournalofBeijingInstituteofTechnology,2005,25(4)：352-355.

[3] 全国信息技术标准化技术委员会.GB/T18284-2000.快速响应矩阵码[S]. 北京：中国标准出版社，2000.

[4] 黄宏博.QR二维条码的纠错编码算法研究及实现[J].微计算机信息,2010,26(30):36-38.

[5] 张兴华.矩阵式快速QR码的研究和应用[D].成都:电子科技大学,2009.

[6] 吴祖义.RS码软判译码技术的研究[D].南京:南京邮电大学,2010.

[7] 袁东风,张海刚.LDPC码理论与应用[M].北京:人民邮电出版社,2008.

[8] 张丽丽.LDPC码构造及其应用研究[D].杭州：杭州电子科技大学,2011.

[9] 贺鹤云.LDPC码基础与应用[M].北京:人民邮电出版社,2009.

[10]XiaoYouan,LuoChunling,YangChao.ThecomparativeanalysisofLDPCandRScode[C].Hangzhou:InternationalConferenceonConsumerElectronics,CommunicationsandNetworks,2011.

Error Correction Improvement Algorithms of QR Code

KANG Weici，CAO Min

(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology, Shanghai 200093, China)

Compared two dimensional barcode with one dimensional barcode, the former does not need to rely on database, and it can store large amount of information and express a variety of multimedia and text information, having error correction ability. For traditional QR code the error correction ability is limited, this paper proposes a solution that error correcting codes LDPC codes will replace RS code to the QR image, it means that use the new correction technology to generate QR code. It gives a study of the error correction code LDPC codes encoding thinking and performance simulation, and then puts it with the RS code simulation contrast. The result shows that compared with the original RS error correcting code, the error correcting capability of the new error correcting LDPC code is improved.

QR code; two-dimensional code; RS code; LDPC code

10.16180/j.cnki.issn1007-7820.2016.12.028

2016- 02- 14

康伟慈(1993-)， 女，硕士研究生。研究方向：软件开发及测试。

TP391.41

A

1007-7820(2016)12-101-03