倒立摆系统控制研究

辛 静，赵高晖，李天箭，杨培培

(上海理工大学 机械工程学院，上海 200093)



倒立摆系统控制研究

辛 静，赵高晖，李天箭，杨培培

(上海理工大学 机械工程学院，上海 200093)

基于复杂的二阶非线性倒立摆系统的不确定性问题，提出了一种自适应该系统的控制方案。通过倒立摆系统的动态方程，利用RBF神经网络对未知函数的逼近，并结合自适应滑模控制算法，建立RBF自适应滑模控制器，谋求解决非线性不确定的倒立摆系统，对该系统进行Matlab仿真验证，并分别对RBF自适应PID控制、普通RBF自适应滑模算法和文中RBF自适应滑模算法进行仿真比较，仿真比较结果验证了该方案不仅具有可行性和有效性，且在时间上具有快速响应性和稳定性。

倒立摆；动态方程；RBF神经网络；自适应滑模控制；Matlab仿真

倒立摆系统控制研究涉及了数字控制、 机器人技术、自动化控制等多种领域、多个技术的有机结合，且本身系统又是一种不稳定、多变量和快速运动的非线性系统[1-4]。所以，研究学者尝试通过倒立摆这样典型的被控对象，检验出新的控制方法是否有较强的处理多变量、非线性及不稳定系统等问题的能力[5-7]。

本文以倒立摆系统为研究对象，因RBF网络具有良好的泛化能力，网络结构简单，避免过多的计算，并能在一个任意精度紧凑集合下逼近任何非线性函数[8-10]。将结合滑模自适应控制用于倒立摆系统中，谋求能够获得较好的动态性能和稳态性能，实现对倒立摆控制仿真，验证该算法的可行性和有效性，并与其他算法仿真比较，表明本文算法的优势[9-11]。

1 控制器设计

SISO倒立摆控制系统中输入项为期望控制的摆杆位置角度θd；输出项为实际摆杆位置角度θ。针对倒立摆控制系统动态方程[10-11]

(1)

其中，x1和x2分别为角位移和角速度;u为控制量输入。且有

针对上述模型，设计控制器，即由滑模函数

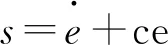
(2)

其中，常数c>0;角位置误差e=θd-θ，进而设计控制律为

(3)

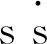
设计RBF网络输入输出算法为

(4)

f′(x)=W*Thf(s)+εf

g′(x)=W*Thg(s)+εg

(5)

其中，x为网络输入；j表示网络输入层第j个的输入；h=[hj]T为高斯基函数的输出；W*和V*分别为逼近f′(x)和g′(x)的理想网络权值；εf和εg为网络逼近误差，|εf|≤εMf,|εg|≤εMg。取[x1x2]T，则RBF网络的高斯基函数。设计控制律为

(6)

其中，η≥D。由式(3)～式(6)推出Lyapunov函数

(7)

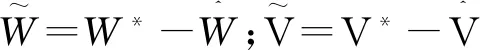
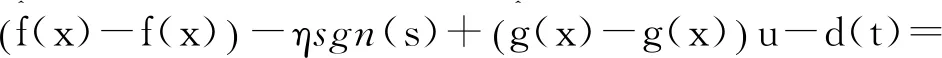
(8)

其中,

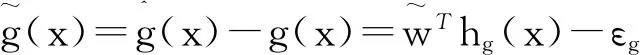
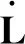
(9)

所以取自适应律为

(10)

2 仿真研究

基于上述控制器设计分析，为验证本文算法在倒立摆非线性不确定系统的可行性和有效性，结合式(1)的动态模型作为被控对象，进行Matlab仿真[3-6]。其中,g=9.8 m/s2;mc=1 kg为小车质量；m=0.1 kg为摆杆质量；l=0.5 m为摆长的一半；设定输入值指令为0.1×sin(t);周期为2πs[4-5]。

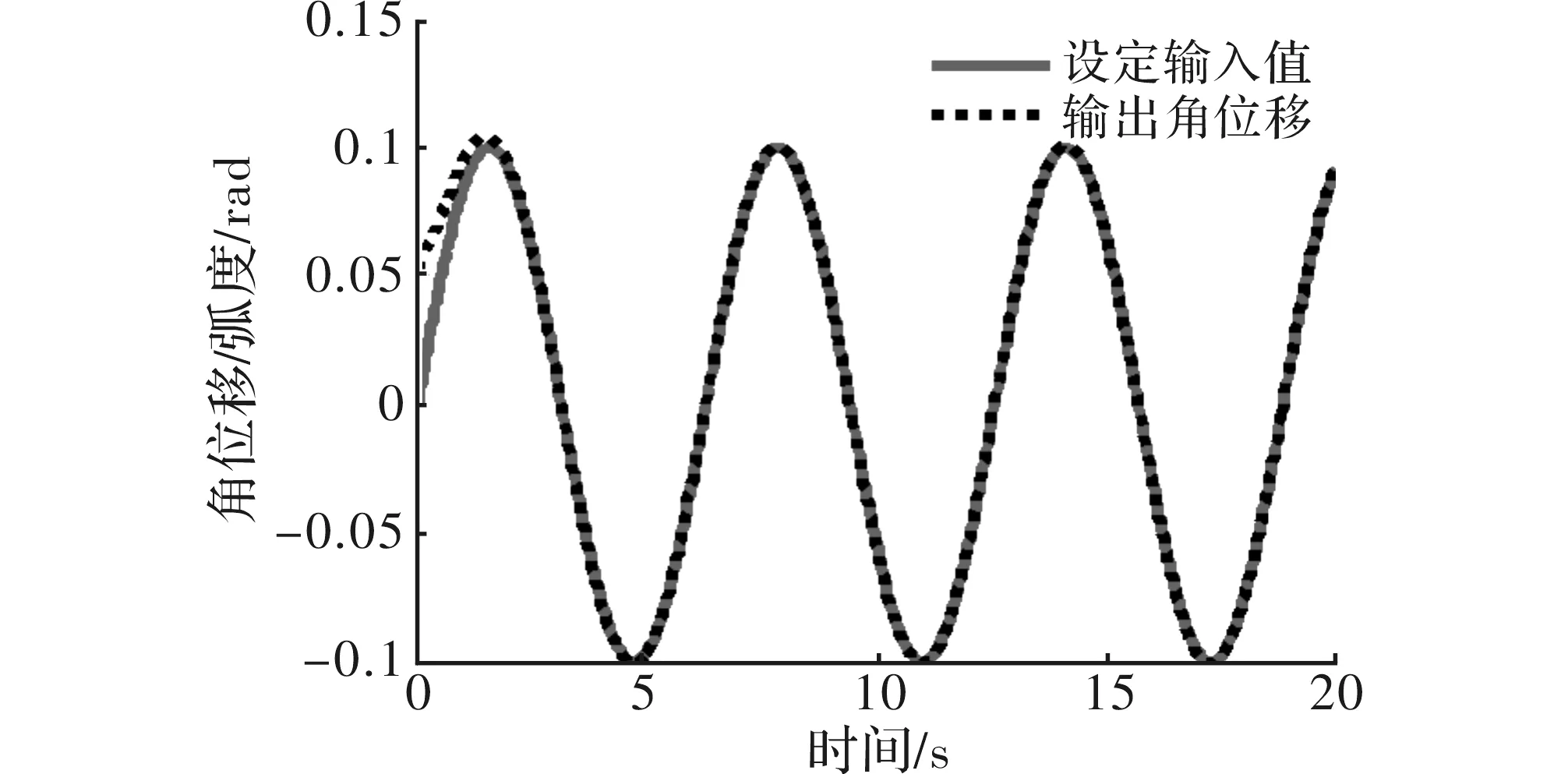
图1 RBF自适应PID控制位置跟踪图

图2 RBF自适应PID控制输入值

仿真结果如图1和图2所示，其中RBF网络结构为2-5-1；权值为0；c=0.1；自适应参数为γ=100；P=11;I=0.01;D=19。从图1可以看出，仿真结果3 s后，理想跟踪位置与仿真跟踪结果位置的两曲线波形基本吻合。从图2可以看出，RBF自适应中算法在1 s内快速学习后，其输入值渐进平滑，结合图1分析，设定输入位置和仿真结果输出的角位移在3 s后才能达到跟踪效果。

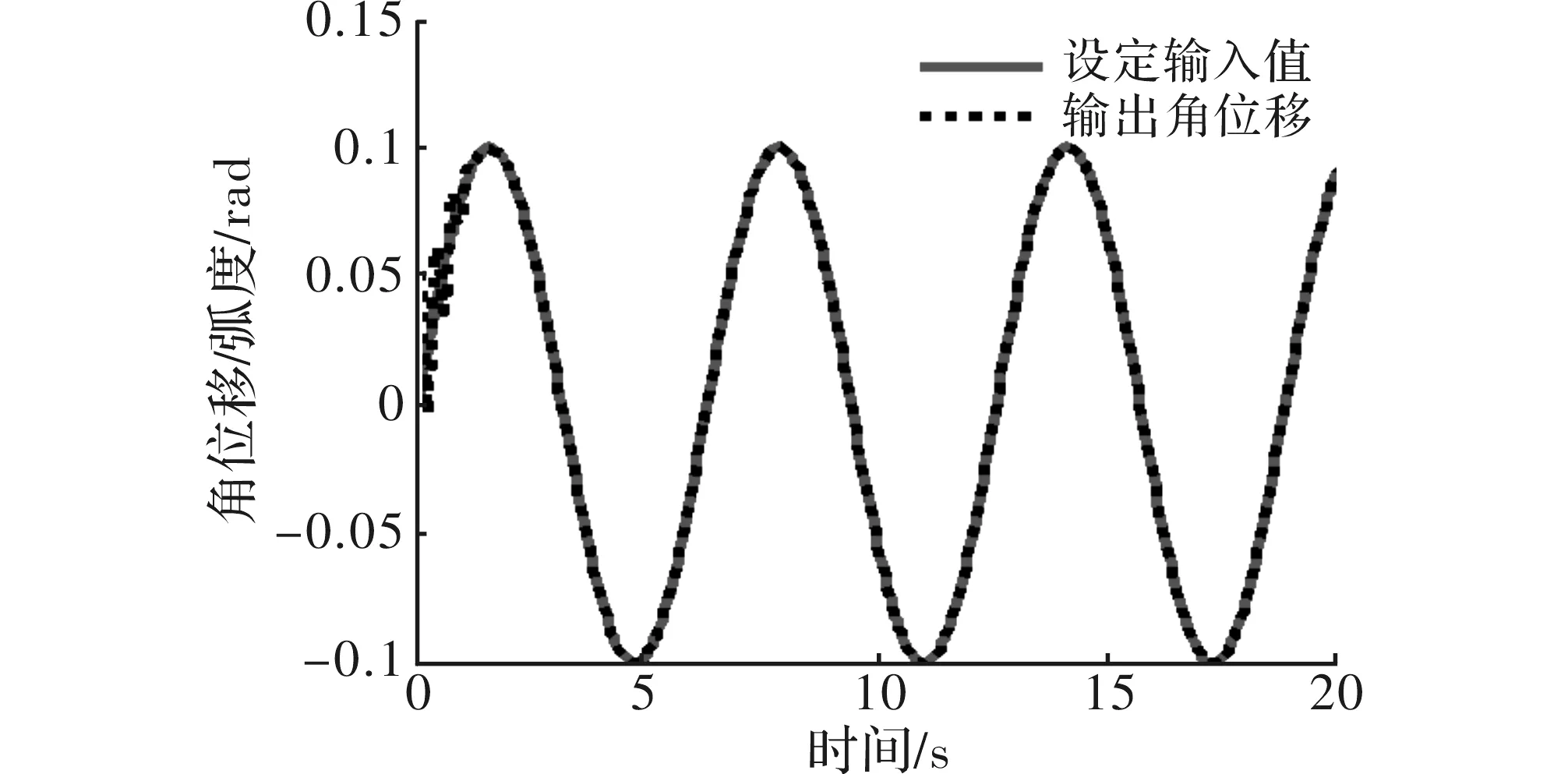
图3 普通RBF自适应滑模控制位置跟踪图

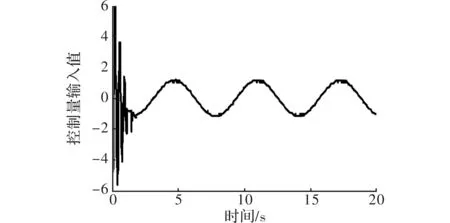
图4 普通RBF自适应滑模控制输入值

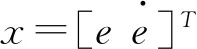
从图3可以看出，仿真结果2s后，理想跟踪位置与仿真跟踪结果位置的两曲线波形基本吻合。从图4可以看出，RBF自适应中算法在2s内自适应学习后，其输入值渐进平滑，结合图3分析，设定输入位置和仿真结果输出的角位移在2s后才能达到跟踪效果。且图3与图1在误差上直观比较可看出，图3仿真结果的误差比图1小，且超调量相对较小。总体来说普通RBF自适应滑模控制仿真结果优于RBF自适应PID控制。

图5 本文RBF自适应滑模控制位置跟踪图

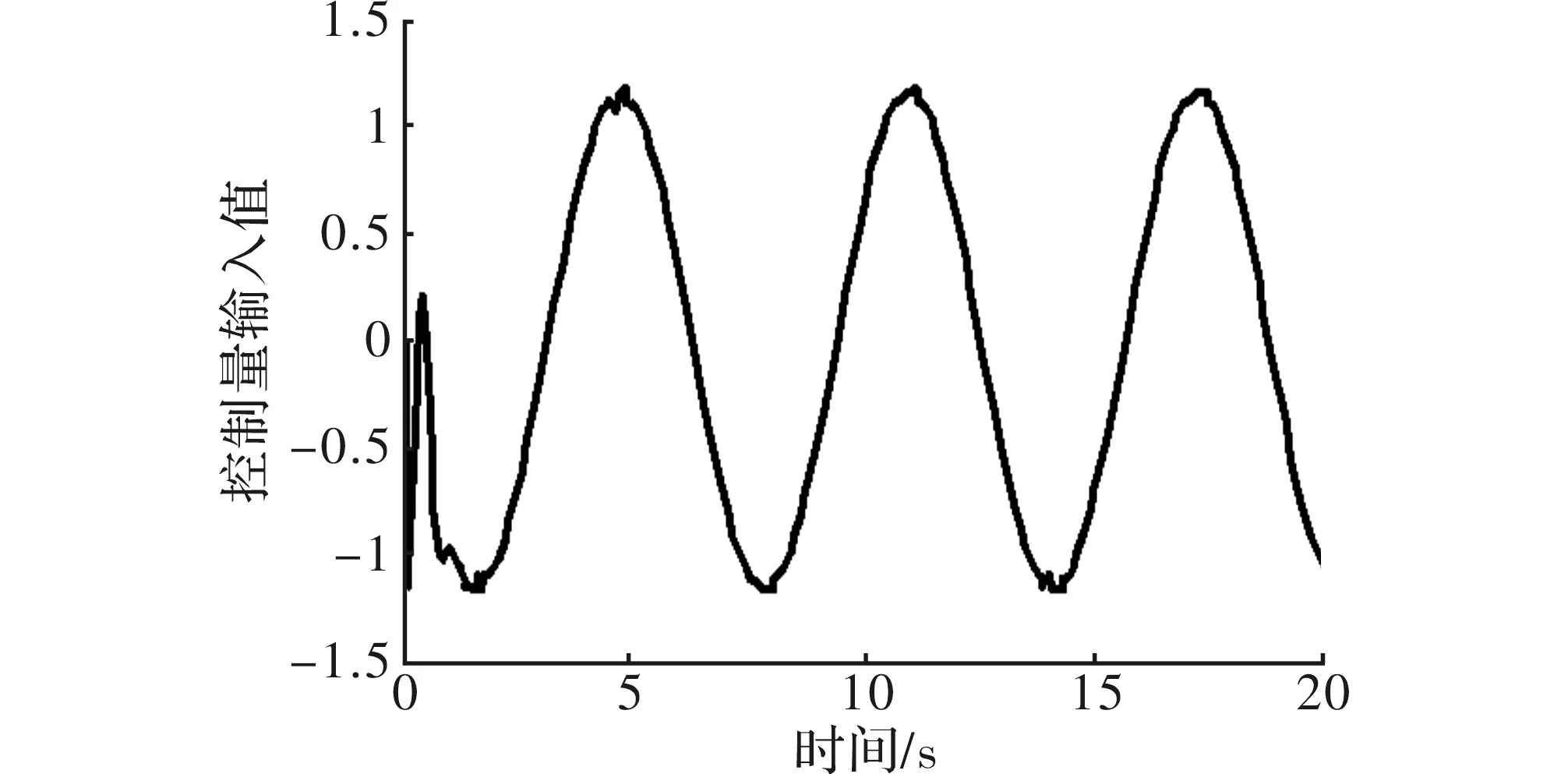
图6 本文RBF自适应滑模控制输入值

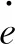
通过输入设定值与仿真结果的位置跟踪图比较和控制输入值的比较，从横向时间上反应本文算法在倒立摆仿真应用中有快速响应的优势，从纵向体现了本文算法在倒立摆仿真应用中有较好的控制精度。

3 结束语

对倒立摆问题分别在RBF自适应的PID控制、普通RBF自适应的滑模控制及本文算法进行仿真比较，本文RBF自适应滑模算法的仿真结果最优。Matlab仿真结果表明，本文RBF自适应滑模控制法是有效、可行的，设计的控制器对倒立摆的平衡稳定性效果较好，满足控制要求。

[1] 王继军,孙灵芳.倒立摆系统概述[J].自动化技术与应用,2011,30(2):1-5.

[2] 舒怀林.基于PID神经网络的倒立摆控制系统[J].机床与液压,2008,36(3):141-143.

[3] Bouslama F,Ichikawa A.Application of neural network to fuzzy control[J]. Neural Networks,1993(6):791-799.

[4] 刘金琨.先进PID控制Matlab仿真[M].3版.北京:电子工业出版社,2011.

[5] 刘金琨.滑模变结构控制Matlab仿真[M].2版.北京:清华大学出版社,2012.

[6] Park J H,Sandberg I W.Universal approximation using radial-basis-function networks[J].Neural Computation,2008,3(2):246-257.

[7] 刘金琨.RBF神经网络自适应控制Matlab仿真[M].北京:清华大学出版社,2014.

[8] 张朋朋.基于神经网络的倒立摆控制方法及其应用研究[D].开封:河南大学,2014.

[9] 胡海旭,罗文广.基于神经网络仿射非线性系统滑模自适应控制[J].电子科技,2014,24(4):12-14.

[10] 王彪,唐超颖,沈春林.利用遗传算法进行PID参数寻优的倒立摆控制系统[J].计算机测量与控制,2004,12(12):1171-1174.

[11] 李虹,熊诗波,孙志毅.Simulink环境下倒立摆控制系统建模与仿真[J].太原科技大学学报,2005,26(3):190-193.

[12] 杨德,沈俊霞.基于神经网络的模型参考自适应控制[J].电子科技,2005(5):48-50.

[13] 苏宇逍.基于GA的BP神经网络在多目标优化中的应用[J].电子科技,2015,28(6):51-53.

[14] 温浩,赵国庆.基于Matlab神经网络工具箱的线性神经网络实现[J].电子科技,2005(1):26-29,33.

[15] 刘田翠,王红然,汪小平.基于自适应神经元的谐波检测方法研究[J].电子科技,2009,22(2):60-63.

Research of Control Inverted Pendulum System

XIN Jing，ZHAO Gaohui，LI Tianjian，YANG Peipei

(School of Mechnical Engineering, University of Shanghai for Science and Technology,Shanghai 200093, China)

Uncertainty problem of basing on complex two order nonlinear inverted pendulum system, this paper put forward a kind of controlling scheme that adapt above system. By means of dynamic equation of the inverted pendulum system, using RBF neural network to approximate the unknown function, combining with the adaptive sliding mode control algorithm, this paper build adaptive sliding mode controller and seek a solution to solve the uncertain nonlinear inverted pendulum system, then the system is simulate and verify by Matlab simulation. In the end, this paper simulate and compare the RBF adaptive PID control, the common RBF adaptive sliding mode algorithm and the RBF adaptive sliding mode algorithm. The result of simulation and comparison show that the control scheme not only has the feasibility, effectiveness, but also it is fast response and stablization in time.

inverted pendulum; dynamic equation; RBF neural network; adaptive sliding mode control; Matlab simulation

10.16180/j.cnki.issn1007-7820.2016.12.044

2016- 03- 04

国家自然科学基金资助项目(51405300)

辛静(1991 -)，女，硕士研究生。研究方向：机械工程方面的智能算法。

TP273

A

1007-7820(2016)12-159-03