基于亚波长光栅衰减模态滤波器的设计与研究

刘清雅，王亚如，唐元开，杜雨晴，王正岭，高传玉

(江苏大学 理学院，江苏 镇江 212013)



基于亚波长光栅衰减模态滤波器的设计与研究

刘清雅，王亚如，唐元开，杜雨晴，王正岭，高传玉

(江苏大学 理学院，江苏 镇江 212013)

采用严格的矢量模态理论，获得有效折射率函数的特征方程，研究模态特性与亚波长光栅填充比及归一化光栅常数的关系，给出衰减模态的条件与特性。利用衰减模态特性，设计分析了一种在利特罗入射条件下的亚波长光栅高通滤波器，得到光栅反射率随波长的响应曲线。在此基础上，设计了一种由两个光栅组成的带通滤波器，选取适当参数，得到了波长在一定范围内的通带滤波器。研究结果为高通滤波器与带通滤波器的实验研究及亚波长光栅器件的实用化提供了参考。

亚波长光栅；衰减模态；滤波器；反射率

亚波长光栅的结构尺度较小，光栅周期小于入射波长，与普通光栅相比表现出许多新颖特性，可用于设计纳米尺度的光子器件[1-3]。2010年，R. L. Chern等人提出了一种利用亚波长周期性金属狭缝结构来研究异常光吸收特性[4]。2011年，M. G. Harats等人提出了一种利用在亚波长金属光栅中的量子点来研究增强双光子过程[5]。2013年，T. Saastamoinen等人提出了一种利用亚波长金属光栅来研究空间相干问题[6]。2014年，Z. L. Wang等人研究了一种亚波长介质/金属/介质周期性结构与光的完美耦合问题[7]。 2016年，唐元开等人采用模态理论研究了TE偏振与TM偏振入射光在一维亚波长光栅区域的模式特性，应用亚波长光栅的模式特性与光栅衍射效率设计了一种偏振分束器[8]。本文在此基础上，给出了衰减模态的条件与特性，利用衰减模态特性，设计分析了一种在利特罗入射条件下的亚波长光栅高通滤波器与带通滤波器。

1 亚波长光栅的模态理论

图1 一维亚波长光栅示意图

图1是一维亚波长光栅的横截面示意图，其中，d为光栅常数，且d=b+g;b是光栅凸起部分(折射率为nb)的宽度;g是光栅凹槽部分(折射率为ng)的宽度;光栅深度为h;光栅的填充比f为b/d。在图1中，入射面(即x-z平面)为光栅横截面，波长为λ的入射光以入射角φin入射到光栅表面。对于亚波长光栅，光栅常数d<λ。

(1)

同理，入射光为TM偏振的特征方程可表示为

cosαd=cos(2πβnxdcf)cos(2πγnxdc(1-f))-

(2)

类似地，通过求解光栅区域电场的亥姆霍兹方程，在z方向的电场部分v(z)可表示为

v(z)=Cexp(ik0neff(z+h))+Dexp(-ik0neff(z+h))

(3)

2 衰减模态与消逝波特性分析

图)随与dc的二维等势线图

图3 模态0与1的随dc和f的变化曲线.

图4 在利特罗入射时，模态0和1关于dc和f的分布图

3 高通滤波器的设计

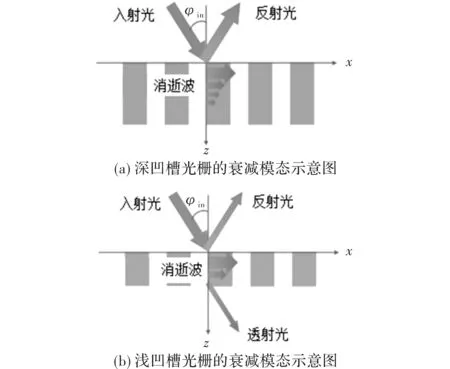
图5 凹槽光栅衰减模态示意图

图随波长λ的变化曲线

根据式 (3) 可得到某个模态m的消逝波经过光栅区域后的透射光振幅，可表示为

Am(h)=Cexp(-k0|neff|h)

(4)

(5)

η=1-ηt

(6)

根据式(1)，式(2)与式(6)，考虑光栅的制造方便及消逝波的特性，在利特罗入射条件下，取f=0.6 ，d=500 nm，h=1 500 nm，可得到光栅的TE与TM偏振总的反射率随波长的响应曲线，如图7所示，λH=1 413.910 8 nm的右侧为反射通带(BAND-PASS)，左侧为反射阻带 (BAND-REJECT)。很明显，图7中右侧通带的响应曲线与理想曲线较为一致，这一波长区域的光波几乎是被完全反射的，η近似为1，处在衰减模态的消逝波不能透射出光栅，从而形成了反射通带。左侧反射阻带的光波能透射出光栅，几乎不能被反射，响应曲线与理想曲线符合。对于λ<500 nm，即cc>1的情况，此时为传播模态，所以入射光可透射出光栅，这个范围全处于反射阻带。对于λ>2 500 nm的情况，此时dc<0.2，即不存在传播模态，入射光将被全反射形成反射通带。图7 中两张插图自上而下分别为TE与TM偏振单独激发时的响应曲线，两条曲线相似，也与普通光的响应曲线近似。因此，选取适当参数，这种亚波长光栅实现了高通反射滤波器的功能。

图7 亚波长光栅高通滤波器响应曲线

上述滤波器实现了高通反射滤波器的功能，若将上述亚波长光栅的透射光作为通带，反射光看作阻带，则便实现了低通滤波的功能。所以用两个亚波长光栅滤波器组合就能实现带通滤波器的功能。如图8所示，入射光首先入射光栅1，其反射光作为通带，透射光作为阻带，反射光入射光栅2后形成的透射光作为带通滤波器的通带。根据式(1)，式(2)与式(6)，设光栅1(高通滤波器)的参数与图7中一致，即f=0.6，d=500 nm，则λH=1 413.910 8 nm ；光栅2(低通滤波器)的参数为f=0.6，d=800 nm，则dcL=0.353 6，则λL=2 262.257 3 nm，设两光栅的深度均为h=1 500 nm，则此种滤波器的响应曲线如图9所示。明显，这种滤波器能满足带通滤波器的功能。并通过改变光栅参数，可实现不同通带范围的带通滤波器。

图8 亚波长光栅带通滤波器示意图

图9 亚波长光栅带通滤波器响应曲线

4 结束语

本文采用严格的矢量模态理论，通过求解光栅区域电场的亥姆霍兹方程，利用周期性条件可获得有效折射率函数的特征方程。研究了模态特性与亚波长光栅填充比与归一化光栅常数的关系，给出了衰减模态的条件与特性。对于两个基本衰减模态，若是深凹槽光栅，消逝波不能穿透光栅区域，此时入射光将会在界面发生全反射。利用衰减模态特性，分析设计了一种在利特罗入射条件下的亚波长光栅高通滤波器。选取适当参数，得到光栅反射率随波长的响应曲线，发现反射通带与理想曲线较为一致，波长>1 414 nm 的反射通带的反射率近似为1。又设计了一种由两个光栅组成的带通滤波器，选取适当参数，得到了波长在1 414～2 262 nm范围的通带滤波器。并通过改变光栅参数，可实现不同通带范围的滤波器。研究结果对于高通滤波器与带通滤波器的实验,以及亚波长光栅器件研究的实用化具有重要意义。

[1] 郭楚才,叶卫民,袁晓东,等.亚波长光栅偏振分束器的研究[J].光学学报,2010,30(9):2690-2695.

[2] 周云,叶燕,申溯,等.亚波长光栅结构彩色滤光片研究[J].光学学报,2011,31(1):223-227.

[3] Liu J,Gao H,Zhou J,Liu D.The design of a polarizing beam splitter made from a dielectric rectangular-groove grating[J].Optics & Laser Technology,2009,41(5):622-626.

[4] Chern R L,Chen Y T,Lin H Y. Anomalous optical absorption in metallic gratings with subwavelength slits[J].Optics Express,2010,18(19):3150-3152.

[5] Harats M G,Schwarz I,Zimran A,et al. Enhancement of two photon processes in quantum dots embedded in subwavelength metallic gratings[J].Optics Express,2011,19(2):1617-1625.

[6] Toni S,Lajunen H.Increase of spatial coherence by subwavelength metallic gratings[J].Optics Letters,2013,38(23): 5000-5003.

[7] Wang Z L,Li S Q,Chang R P H,et al.Perfect coupling of light to a periodic dielectric/metal/dielectric structure[J].Journal of Application Physics,2014,11(6):103-108.

[8] 唐元开,王正岭,刘清雅.亚波长光栅的模态特性与衍射效率及其应用[J].电子科技,2016,29(3):118-121.

The Design and Study of Filter Based on Evanescent Mode of Subwavelength Grating

LIU Qingya，WANG Yaru，TANG Yuankai，DU Yuqing，WANG Zhengling，GAO Chuanyu

(School of Science, Jiangsu University, Zhenjiang 212013, China)

The characteristic equations of the effective refractive index function are obtained by the rigorous vector modal theory. The relationship between the modal characteristics and filling ratio as well as the normalized subwavelength grating constant is investigated, and the attenuation condition and characteristics of the attenuation mode are given. A high-pass filter is designed by the characteristics of the attenuation mode under the condition of Littrow-mounting incidence, and the response curve of the reflectivity with the wavelength is given. And a bandpass filter is designed by two gratings based on appropriate parameters. Our result is important for the experimental research and application of high-pass or bandpass filter and the subwavelength grating device.

subwavelength grating; attenuation mode; filter; reflectivity

10.16180/j.cnki.issn1007-7820.2016.12.001

2016- 04- 09

国家自然科学基金资助项目(50975128)；江苏省自然科学基金资助项目 (BK2011462)；江苏省高校自然科学研究重大基金资助项目(15KJA140001)；江苏省大学生创新训练重点基金资助项目(201510299001Z)。

刘清雅(1994-)，女，本科。研究方向：微纳米光学等。王正岭(1971-)，男，博士，教授。研究方向：微纳米光学等。

TN383

A

1007-7820(2016)12-001-05