考虑积雪休止角的屋面积雪漂移数值模拟方法
2016-12-26康路阳周晅毅同济大学土木工程防灾国家重点实验室上海200092
康路阳,周晅毅,顾 明(同济大学土木工程防灾国家重点实验室,上海200092)
考虑积雪休止角的屋面积雪漂移数值模拟方法
康路阳,周晅毅,顾 明
(同济大学土木工程防灾国家重点实验室,上海200092)
根据风雪运动机理和屋面积雪特点,提出一种考虑积雪休止角的屋面风致积雪漂移数值模拟方法.应用此方法对一平屋盖屋面积雪重分布进行了模拟,随后分析了考虑休止角与否对屋盖雪面附近流场特性的影响,并将数值模拟结果与风洞试验结果进行了对比.结果显示,数值模拟结果与试验数据吻合较好.
积雪漂移;积雪重分布;数值模拟;积雪休止角;平屋盖
雪灾是造成屋盖结构损毁的主要自然灾害之一.雪灾中风致积雪漂移导致屋面积雪产生不均匀分布,不均匀的雪荷载往往对屋盖结构极为不利,因此在结构设计中准确预测屋面积雪分布非常重要.范峰等[1]和刘庆宽等[2]对比分析了国际上主要荷载规范和标准中关于屋面雪荷载的规定.然而,当前这些荷载规范或标准[3-7]有关雪荷载的规定主要依据工程经验和有限的实测数据,缺乏严格的理论依据.
除均匀分布雪荷载外,滑移雪荷载与漂移雪荷载是屋面雪荷载的主要形式.滑移雪荷载方面的研究偏少.Zhou等[8-9]提出了屋面滑移雪荷载计算模型,并计算了我国典型有雪城市滑移雪荷载系数.有关雪荷载的研究主要集中在漂移雪荷载方面.风洞试验是研究漂移雪荷载的有效手段.刘庆宽等[2]和Zhou等[10]在风洞中采用硅砂等模拟雪颗粒,研究了典型屋盖屋面的积雪分布.近些年来,随着计算技术的发展,有关学者开始利用计算流体动力学(CFD)方法研究雪漂移现象.Beyers等[11]在对一个立方体周边雪漂移模拟时考虑了击溅流的影响,利用南极科考站SANAE IV的实测数据,对模拟结果的准确性进行了详细分析.周晅毅等[12]使用数值模拟的手段对首都国际机场3号航站楼屋面雪荷载分布进行了研究.Thiis等[13]采用两相流数值模拟方法对一个大跨曲面屋盖的屋面积雪沉积进行了瞬态模拟,并将模拟结果与实测结果进行了对比.王卫华等[14]根据雪深变化采用时变边界,对一典型阶梯形屋面积雪分布进行了数值模拟.与建筑周边雪漂移不同的是,雪沉积在屋盖表面时会在屋盖边缘形成休止角,这将影响屋盖表面的风雪运动.然而,目前没有学者在屋面积雪漂移数值模拟中考虑这一因素.
初始积雪外形和积雪外形的改变都会对风雪运动产生影响.为解决这些问题,本文提出一种考虑积雪休止角的屋面风致积雪漂移数值模拟方法.数值模拟时在初始积雪外形中考虑积雪休止角,同时对风吹雪过程进行分时段处理,每一时段采用定常计算方法.本文应用此方法对一平屋盖屋面积雪漂移进行了模拟.随后详细分析了考虑休止角与否对屋盖雪面附近流场特性的影响,并将考虑休止角的屋盖积雪重分布数值模拟结果与风洞试验结果进行了对比.
1 数值模拟方法
1.1 计算方法与流程
对空气相和雪相分别建立传输方程.风场模拟采用Reynolds时间平均法,雪相模拟采用欧拉方法.风雪之间的影响为单向耦合,即雪在风的作用下发生漂移,而雪的搬运、堆积过程对空气不产生影响.壁面上雪的侵蚀与沉积通过计算壁面雪通量获得.限于篇幅,空气相控制方程、雪相控制方程与壁面雪通量计算的详细介绍见文献[12].
因长时间风吹雪过程引起的积雪侵蚀/沉积,必会造成建筑屋面积雪外形的改变,对屋盖周围的流场产生影响.另一个问题是,自然界一次风吹雪可能长达几小时至数天的时间,如果采用传统CFD瞬态方法进行非定常计算,将导致巨大的计算量.针对上述问题,为了兼顾计算效率与模拟的准确性,本文将屋面雪的迁移过程分成若干时间段,在这些时间段内采用单向耦合的定常方法计算屋面积雪的迁移;为考虑雪层高度变化的影响,利用本时段内积雪高度变化的计算结果,重新建立屋面积雪边界来进行下一个时段的定常计算.该方法的计算步骤如下:
(1)根据气象部门提供的气象数据,将某次风吹雪持续时间T分为n段,第i段时间长度用Δti来表示.
(2)采用定常方法求解空气相控制方程,得到第i时间段的平均风速场,从而求得雪面的摩擦速度u*.
(3)根据步骤(2)的计算结果,采用定常、单向耦合的方法[12]求解雪相控制方程,获得第i时段内单位时间积雪高度改变率Δhi=qi/ρs.q为壁面雪通量,ρs为积雪密度.
(4)由下式计算第(i+1)时段初始雪面高度:
hi+1=hi+ΔhiΔti(1)
式中:hi、hi+1分别为第i、第(i+1)时段初始积雪高度.计算得到更新后的屋面外形后,重新建立用于CFD分析的模型[14].
(5)重复步骤(2)~(4),得到风吹雪持续时间T后的屋面积雪分布.
尽管在每一时间段内采用了单向耦合的方法,但由于在下一时间段内通过雪面外形的改变而考虑了风雪过程对流场的影响,这也就在很大程度上反映了雪颗粒运动对风场的反馈作用.
1.2 积雪休止角
雪颗粒自然下落所能稳固保持的最大倾斜角度为积雪休止角.积雪休止角会改变屋面积雪边缘流动分离位置,对屋面的流动分离强度以及迎风前缘的摩擦速度都会有较大的影响.积雪休止角对屋面积雪漂移影响的详细分析见第4.1节.新降雪沉积在屋盖表面会形成一定休止角,考虑休止角会使模拟结果与实际屋面雪漂移更为接近.因此,本文在模拟初始积雪外形时考虑了积雪休止角.
积雪休止角与雪颗粒表面不规则性、颗粒之间的黏结性密切相关.积雪休止角随着颗粒不规则性的增加和环境温度的上升而变大.粉状雪颗粒在-35.0~-3.5℃时,积雪休止角为45°~55°,在接近融化点时可达90°[15].本文数值模拟假定新降积雪处于0℃以下,取积雪休止角为50°.
2 数值模型
2.1 研究对象
由于平屋盖是许多现行荷载标准和规范[3-7]中屋盖雪荷载计算的重要内容,因此本文选择了平屋盖作为研究对象.研究的平屋盖建筑跨度L为12.0 m、高H为3.0m,见图1.
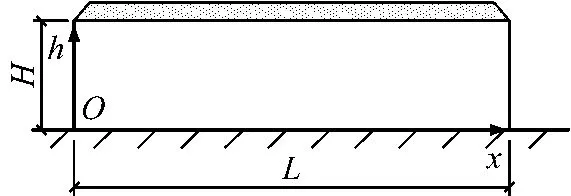
图1 平屋盖尺寸Fig.1 Dimensions of flat roof
2.2 模拟参数与边界条件
数值模拟使用的雪颗粒物理特性见表1.本文没有测量雪颗粒的物理属性,其值参考相关文献确定[15-16].

表1 雪颗粒物理属性Tab.1 Physical properties of snow particle
在商业软件FLUENT中模拟了该二维平屋盖原型,入口风剖面采用Yang等[17]建议的自保持大气边界层条件,表示如下:
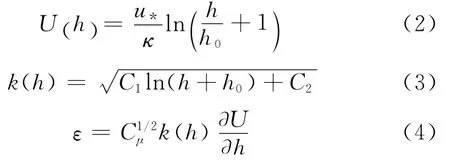
式中:h0为气动粗糙高度;U(h)为h高度处平均风速;κ为冯卡曼常数;C1、C2为拟合常数;k(h)为h高度处湍动能;ε为耗散率;Cμ为模型常数.式(2)~(4)中的常数可根据文后风洞试验的入流剖面拟合得到.
由于本文并没有一个确定的原型建筑及其相关的气象条件,于是作为一个工程的应用,这里取原型屋面初始雪厚度50cm,并将10m高度处的原型风速确定为6.4m·s-1.将风洞试验风剖面测量数据和风剖面式(2)进行拟合,可确定u*为0.35m· s-1,h0为0.004 26m,进而可以得到原型屋盖高度处风速U(H)=5.4m·s-1.由于一次风吹雪过程可能维持数小时到数天,于是风作用持续时间设置为T=10.3d.按照前面描述的计算流程,将该风吹雪过程分为3段进行模拟,3段时间分别为2.4、5.4、2.5d.
计算模型为实尺模型,计算域尺寸为16L× 30 H.风场计算采用时均Realizablek-ε模型.因k-ε模型是高雷诺数模型,只能处理湍流核心区的流动,因而在壁面区选用标准壁面函数求解流动物理量.出流采用完全发展出流边界条件,流域顶部采用自由滑移壁面条件,屋盖表面和地面采用无滑移壁面条件.网格方案采用结构化的渐进网格,网格增长因子为1.1,网格总数为1.84万.这里的网格划分方案保证了结果不随网格大小的改变而发生显著的变化.收敛标准为量纲一残差降至10-6以下且屋盖前缘控制点风速达到稳定.
3 风洞试验
文献[18]使用高密度硅砂对此平屋盖屋面的积雪漂移进行了缩尺模拟.试验在同济大学TJ-1风洞完成.风洞试验的几何缩尺比为1∶25,模型屋面的初始雪厚度为20mm.风洞试验的平均风速剖面见图2a,湍流度剖面见图2b,湍动能剖面见图2c.图中横纵坐标皆为量纲一值,U(H)和k(H)为屋盖高度处风速与湍动能,I为湍流强度.其中,湍动能由试验风速与试验湍流度获得.试验屋盖高度处风速为7.0 m·s-1,湍流度约为13%.风洞试验分3段进行,每个时段风作用持续时间为1min.数值模拟保证了风速相似参数和时间相似参数与风洞试验相同.相关相似参数的介绍见文献[10].

图2 入流风剖面Fig.2 Approaching wind profile
4 数值模拟结果
4.1 流场特性
图3给出了初始时刻平屋盖屋面周边的风速矢量图.若不考虑积雪休止角(即休止角为90°),风速矢量图如图3a所示,来流在迎风前缘点A发生强烈分离,形成一个大尺度旋涡附着在屋面上方.此时,屋盖雪面迎风侧大部分区域的近壁面风速与来流方向相反.考虑积雪休止角的计算结果见图3b,在来流的作用下,屋盖积雪前缘流动分离点为B点和C点.由于考虑了积雪休止角,流动分离强度相对于直角情况明显削弱,靠近雪面的风速方向与雪面大致平行,同时从风速矢量图(见图3b)中也观察不到迎风前缘有明显的旋涡.可见在屋盖表面积雪重分布数值模拟中必须考虑积雪休止角,否则屋面附近的流场有较大的差别,这将导致屋面雪荷载的分布有较大的差异.
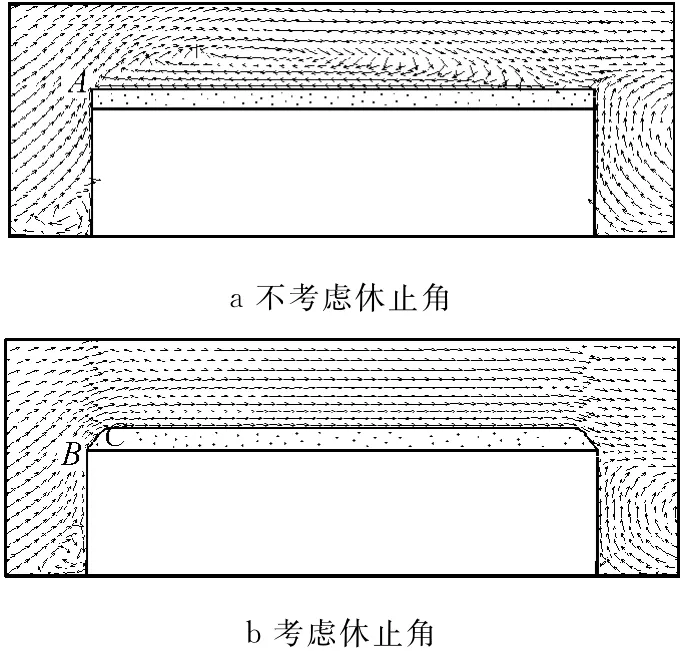
图3 雪面附近风速矢量图(初始时刻)Fig.3 Velocity vectors around snow surface(initial time)
图4给出了初始时刻屋盖积雪及建筑周边雪质量浓度.在初始积雪外形下,积雪表面附近雪质量浓度处于20~60g·m-3之间,只在雪面后缘很小的区域雪质量浓度略大于60g·m-3.从图4中可观察到,积雪表面雪质量浓度从前缘到后缘逐渐增大.结合风速矢量图(见图3b)可知,雪被吹离雪表面后沿顺风向向屋盖后缘运动,致使屋盖后缘雪质量浓度最大.可见,数值模拟反映出了来流作用下积雪在屋盖上方的迁移情况.
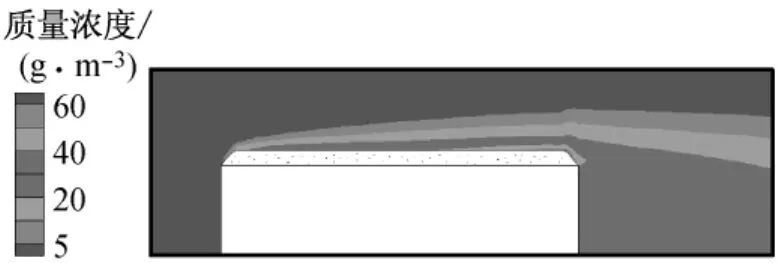
图4 屋盖周边雪质量浓度(初始时刻)Fig.4 Snow concentration around roof surface (initial time)
4.2 雪面摩擦速度
图5对比了初始时刻模拟休止角与不模拟休止角2种情况下雪面的摩擦速度分布.初始积雪外形如果考虑休止角,整体上雪面摩擦速度均大于阈值,只在屋盖尾缘很小部分摩擦速度低于阈值.摩擦速度在屋盖前缘较大,峰值达到阈值的2.5倍以上.在屋盖中后部,摩擦速度沿跨度变化较为平缓,维持在0.25m·s-1附近.在屋盖尾缘,摩擦速度略微上升,局部极值超过0.30m·s-1.数值模拟时,初始积雪外形如果不考虑积雪休止角,雪面摩擦速度将整体低于阈值.摩擦速度除在屋盖前缘与后缘有小幅波动外,沿跨度摩擦速度先增大后减小,跨中峰值仅为0.18m·s-1,未超过阈值0.20m·s-1.可见,如果数值模拟中不考虑积雪休止角,屋面积雪将不会发生侵蚀,也就是说当屋盖高度处风速为5.4m·s-1时,屋面积雪不会产生重分布现象,这与风洞试验结果不符,因而在数值模拟中必须考虑积雪休止角.
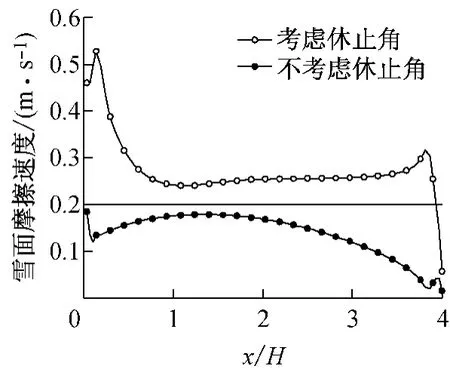
图5 雪面摩擦速度(初始时刻)Fig.5 Friction velocity on roof surface(initial time)
4.3 屋面积雪分布
图6对比了雪漂移结束时刻数值模拟和风洞试验获得的平屋盖屋面的积雪分布.图6中,量纲一积雪深度为结束时刻屋面积雪深度S与初始积雪深度S0(原型50cm;模型20mm)的比值.数值模拟结果与风洞试验结果吻合较好,但在平屋盖的迎风前缘(约占跨度的25%)数值模拟结果偏大.
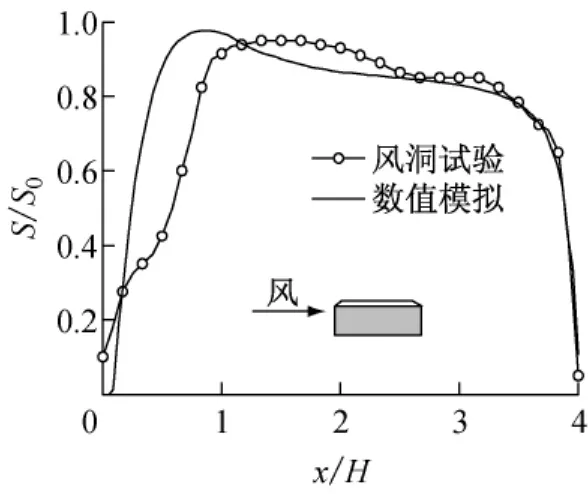
图6 屋面积雪分布(结束时刻)Fig.6 Snow distribution on roof surface(final time)
在原型屋盖高度处风速为5.4m·s-1时,平屋盖积雪整体上表现为侵蚀,屋盖前缘与后缘积雪侵蚀较多.在屋盖中部积雪沿跨度侵蚀量缓慢增加,数值模拟与风洞试验都预测出了这一变化趋势.积雪侵蚀最少位置在屋盖中前部,数值模拟预测出的侵蚀最少的位置比风洞试验预测出的位置更靠近屋盖前缘.
5 结论与展望
(1)提出了一种考虑积雪休止角计算屋面积雪重分布的数值模拟方法.该方法可结合气象数据对风吹雪进行分段定常模拟,在下一时间段内通过重新建模考虑雪面外形的改变对流场的影响.经试验验证,预测结果较准确.本文提出的方法,因考虑了初始积雪的积雪休止角,更能反映屋盖表面风吹雪的实际情况.
(2)屋面初始积雪外形对屋面雪漂移运动影响很大,0℃以下新降雪沉积在屋盖表面会保有一定休止角.从比较分析可见,如果没有考虑休止角,屋面附近的流场有较大的差别,这将导致屋面积雪分布有较大的差异,与试验结果不符,数值模拟必须考虑这一因素.因而,如果采用数值模拟方法确定屋面雪荷载,应考虑沉积在屋盖边缘积雪的休止角.
使用数值模拟方法预测屋面雪荷载有较好的应用前景,今后可在建筑屋面女儿墙、檐口等设置方面进行进一步研究.本文将提出的方法应用于二维建筑,今后可进一步将此方法推广应用到三维情况,使其可用于复杂建筑屋盖表面漂移雪荷载的预测.同时,在今后数值模拟中,可结合气象数据采集频率特点,将时间步进一步细化.
[1]范峰,莫华美,洪汉平.中、美、加、欧屋面雪荷载规范对比[J].哈尔滨工业大学学报,2011,43(12):18.FAN Feng,MO Huamei,HONG Hanping.Comparison of snow load requirements in design codes used in China,USA,Canada and EU[J].Journal of Harbin Institute of Technology,2011,43(12):18.
[2]刘庆宽,赵善博,孟绍军,等.雪荷载规范比较与风致雪漂移风洞试验方法研究[J].工程力学,2015,32(1):50.LIU Qingkuan,ZHAO Shanbo,MENG Shaojun,et al.Codes comparison and wind tunnel simulation of wind-induced snowdrift[J].Engineering Mechanics,2015,32(1):50.
[3]International Organization for standardization.Bases for design of structures:determination of snow loads on roofs[S].3rd ed.Geneva:International Organization for Standardization,2013.
[4]CEN.Euro code 1:actions on structures.Part 1-3:general actions-snow loads(EN1991-1-3)[S].Brussels:European Committee for Standardization,2003.
[5]National Research Council of Canada.National building code of Canada 2005[S].Ottawa:NRCC,2005.
[6]American Society of Civil Engineers.Minimum design loads for buildings and other structures(ASCE/SEI 7-10)[S].Reston:ASCE Press,2010.
[7]中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局.GB 50009—2012建筑结构荷载规范[S].北京:中国建筑工业出版社,2012.Ministry of Construction of the People’s Republic of China,General Administration of Quality Supervision,Inspection and Quarantine of the People’s Republic of China.GB50009—2012 Load code for the design of building structures[S].Beijing:China Architecture &Building Press,2012.
[8]ZHOU Xuanyi,ZHANG Yunqing,GU Ming,et al.Simulation method of sliding snow load on roofs and its application in some representative regions of China[J].Natural Hazards,2013, 67(2):295.
[9]ZHOU Xuanyi,LI Jialiang,GU Ming,et al.A new simulation method on sliding snow load on sloped roofs[J].Natural Hazards,2015,77(1):39.
[10]ZHOU Xuanyi,HU Jinhai,GU Ming.Wind tunnel test of snow loads on a stepped flat roof using different granular materials [J].Natural Hazards,2014,74(3):1629.
[11]Beyers J H M,SundsbØP A,Harms T M.Numerical simulation of three-dimensional,transient snow drifting around a cube[J].Journal of Wind Engineering and Industrial Aerodynamics,2004,92(9):725.
[12]周晅毅,顾明,朱忠义,等.首都国际机场3号航站楼屋面雪荷载分布研究[J].同济大学学报:自然科学版,2007,35(9):1193.ZHOU Xuanyi,GU Ming,ZHU Zhongyi,et al.Study on snow loads on roof of terminal 3 of Beijing capital international airport[J].Journal of Tongji University:Natural Science,2007,35(9):1193.
[13]Thiis T K,Potac J,Ramberg J F.3D numerical simulations and full scale measurements of snow depositions on a curved roof[C/OL]//EACWE,Florence.[2014-12-30].http://iawe.org/Proceedings/5EACWE/104.pdf.
[14]王卫华,廖海黎,李明水.基于时变边界屋面积雪分布数值模拟[J].西南交通大学学报,2013,48(5):851.WANG Weihua,LIAO Haili,LI Mingshui.Numerical simulation of wind-induced roof snow distributions based on time variable boundary[J].Journal of Southwest Jiaotong University,2013,48(5):851.
[15]Kuroiwa D,Mizuno Y,Takeuchi M.Micromeritical properties of snow[C/OL]//International Conference on Low Temperature Science:Physics of Snow and Ice.[2014-12-30].http://133.87.26.249/dspace/bitstream/2115/20340/1/2_p7.
[16]Tominaga Y,Okaze T,Mochida A.CFD modeling of snowdrift around a building:an overview of models and evaluation of a new approach[J].Building and Environment,2011,46(4):899.
[17]Yang Y,Gu M,Chen S,et al.New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering[J].Journal of Wind Engineering and Industrial Aerodynamics,2009,97 (2):88.
[18]胡金海.建筑屋盖表面风致积雪运动的实验研究[D].上海:同济大学,2013.HU Jinhai.Experimental study on wind-induced snow motion on building roof surface[D].Shanghai:Tongji University,2013.
Numerical Simulation Method About Snowdrift on Roofs With Consideration of Repose Angle of Snow
KANG Luyang,ZHOU Xuanyi,GU Ming
(State Key Laboratory for Disaster Reduction in Civil Engineering,Tongji University,Shanghai 200092,China)
Based on the mechanism of snowdrift and the characteristics of snow redistribution on roofs,a numerical simulation method about snowdrift on roofs was proposed with consideration of repose angle of snow.Then,the snow redistribution on a flat roof was simulated by the method.The effect of repose angle of snow on the characteristics of flow field around flat roof was also analyzed.Finally,the numerical results of snow redistribution were compared with those from wind tunnel tests.It is shown that simulation results are in good agreement with experimental data.
snowdrift;redistribution of snow;numerical simulation;repose angle of snow;flat roof
TU312
A
0253-374X(2016)01-0011-05
10.11908/j.issn.0253-374x.2016.01.002
2015-03-26
科技部国家重点实验室基金(SLDRCE14-B-10);中央高校基本科研业务费专项资金
康路阳(1991—),男,博士生,主要研究方向为结构风雪工程.E-mail:kangluyang@tongji.edu.cn
周晅毅(1975—),男,副研究员,博士生导师,工学博士,主要研究方向为结构风雪工程.E-mail:zhouxytj@tongji.edu.cn
