摩擦片材料和结构对制动器热弹性失稳影响

夏德茂，奚 鹰，朱文翔，华滨滨（同济大学机械与能源工程学院，上海201804）



摩擦片材料和结构对制动器热弹性失稳影响

夏德茂，奚 鹰，朱文翔，华滨滨
（同济大学机械与能源工程学院，上海201804）

建立了二维摩擦制动器热弹性失稳（TEI）数学模型.基于反对称热点分布模式，采用扰动分析法研究了临界速度、扰动增长系数以及扰动迁移速度的变化规律，讨论和比较了摩擦片厚度、热物理特性参数和有限周向接触弧长对系统稳定性的影响.结果表明：临界速度随扰动频率呈先减小后增大的变化规律；扰动迁移速度在摩擦片和金属盘内随扰动频率呈相反的变化趋势，且扰动在具有较高导热系数的金属盘内的速度几乎为零；增加摩擦片厚度、导热系数、比定压热容和减小弹性模量均可提高滑动摩擦系统的热弹性稳定性.

制动器；热弹性失稳（TEI）；扰动增长系数；临界速度；扰动频率

对于路面、铁路车辆以及航空飞机所装备的摩擦制动器或离合器，在其发生制动或换挡接合的过程中，当金属盘和摩擦片之间的相对滑动速度高于某一临界值时便会引起温度场和接触压力发生不均匀扰动，导致滑动摩擦系统因热弹性耦合作用而进入热弹性失稳（TEI）状态［1］，最终在金属盘面出现局部高温区，并形成热点.热点的产生会加剧材料的磨擦、损伤，导致摩擦副出现低频振动、啸叫和抖动，甚至发生制动失效，严重影响了车辆的行驶安全和乘坐舒适性［2］.Mao等［3］将该现象分为摩擦激励和静态接触2种，前者是由弹性体间相互滑动摩擦引起的，而后者则是在接触面上，由与接触压力相关的热阻引起的.

TEI扰动理论最早是由密歇根大学的Lee等［4］在西北大学Burton等［5］的研究基础上提出，并指出每个滑动摩擦系统均存在发生TEI的临界条件.Zagrodzki等［6］通过对换挡离合器在不同接合速度下热点产生机理的研究后发现，当初始接合速度很高时，即使时间很短，也会在金属盘面上观测到热点，此外结构上存在的微小瑕疵能很大程度触发该缺陷的产生.Ostermeyer等［7］通过研究指出，摩擦面上因滑动摩擦而产生的微小磨损颗粒物能加剧摩擦副的温升和TEI效应，尤以当热点呈环形带状分布时最为显著.Du等［8］研究了由一导热体和一热绝缘体组成的滑动摩擦模型的TEI临界条件，将求解临界速度问题转化为求解系统矩阵特征值问题.Zhao等［9］通过理论建模的方法研究了在流体润滑状态下湿式离合器的TEI临界条件.Painer等［10］通过试验发现，在金属盘面上观测到的热点有焦点型、区域型、形变型、梯度型和粗糙型凸点5种，尤以焦点型热点对制动盘的伤害最大.Kasem等［11］通过试验指出，热点最初出现在制动盘的最外边缘，随着制动的进行，逐渐向盘内径方向发展，盘面高、低温区的温差达到近700°C.

本文以某条快速城市轨道交通车辆所装备的盘式制动器中的摩擦副为研究对象，考虑摩擦片厚度的影响，建立了TEI数学模型.基于反对称热点模式，采用扰动分析法计算和比较了摩擦片材料的弹性模量、比定压热容、导热系数和线胀系数对系统稳定性的影响，得到的结论可为研发新型摩擦制动器和离合器提供一定的理论参考.

1 TEI数学模型

赵家昕等［12］在建立车辆离合器热弹性失稳数学模型时认为，接合过程中仅有少量摩擦热经热传导作用进入摩擦衬片，且摩擦片材料只有表层温度变化比较剧烈.因此，其将摩擦片简化为静止的半无限大材料，即认为摩擦片具有无限大厚度.实际上，由热载荷分配计算式（1）［13］可知，这种假设当且仅当摩擦片材料的导热系数、密度及比定压热容要远小于金属盘时才成立.

式中：δ为滑动摩擦面热载荷分配系数；λ、ρ和cp分别为材料的导热系数、密度和比定压热容；下标1、2分别代表摩擦片和金属盘.

随着列车运行速度的不断提高，传统摩擦片材料已不能满足高制动性能的要求，纸基、复合、粉末冶金等新型摩擦材料也更多地被应用于摩擦副材料的设计与选择过程中.西南大学的李明［14］研究了由25Cr2MoVA制动盘和铜基粉末冶金闸片组成的摩擦副在紧急制动过程中的热力耦合效应，两者的导热系数、比定压热容和密度分别为50 W·（m· K）－1、460J·（kg·K）－1、7 810kg·m－3和34W· （m·K）－1、550J·（kg·K）－1、5 250kg·m－3.由式（1）可知，在制动过程中，大约会有42.51%的热载荷进入摩擦片.若在建立该摩擦副的TEI模型时仍假设摩擦片具有无限大厚度，即认为仅有少量热载荷进入摩擦片，势必会影响计算结果的准确性.因此，考虑摩擦片的实际厚度，本文建立了如图1所示的TEI数学模型.

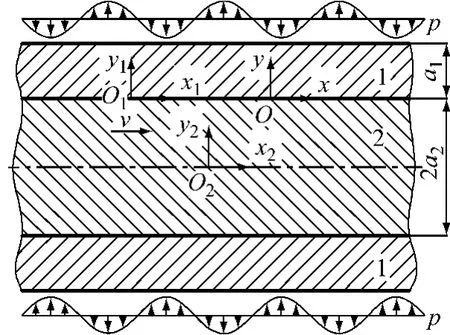
图1 TEI数学模型Fig.1 Mathematical model of thermoelastic instability

图1中，1为摩擦片，2为制动盘，均为轴对称结构，多见于车用离合器，飞机的多盘、片制动器.摩擦片在呈余弦分布的压力扰动p的作用下贴紧制动盘，发生滑动摩擦作用.假设层i的运动速度为vi（i＝1，2），且制动盘相对摩擦片以恒定速度v（v＞0）沿x轴正方向运动.a1、2a2分别为摩擦片和制动盘的厚度.（xi，yi）为层i的静态坐标系，且（x1，y1）固定在滑动摩擦面上，（x2，y2）固定在制动盘的中分面上，（x，y）为摩擦面运动方向上的动态坐标系，扰动在层i内沿x轴方向的速度为ci.

依据文献［4］，将接触压力扰动形式记为

式中：p（x，t）为接触压力的扰动形式；p0为接触压力的扰动幅值；b为扰动增长系数；m为扰动频率；t为时间；j为虚数单位，j＝（－1）0.5.

图1中各坐标系之间存在如下关系：

显然，汽车和火车上所装备的盘式制动器中摩擦片的速度v1＝0，v1、v2和c1、c2存在如下关系：

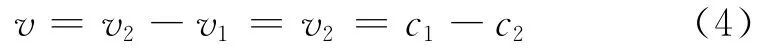
1.1 热点的分布形式

Burton等［5］通过理论分析和试验测试后指出，热点在金属盘的摩擦面上有对称和反对称2种模式.Lee等［4］以汽车盘形制动器为研究对象，建立了一厚度为a的制动盘在2块具有无限大厚度的摩擦片之间做相对滑动运动的TEI模型，求解了不同热点分布模式对应的临界失稳条件.研究结果表明，当热点呈反对称分布时所需的最低临界速度要比对称分布模式低很多.因此，文中后续的理论推导计算和研究均以热点呈反对称分布为前提.

1.2 温度场扰动分析

依据能量守恒定理，摩擦片和制动盘在滑动摩擦过程中应满足

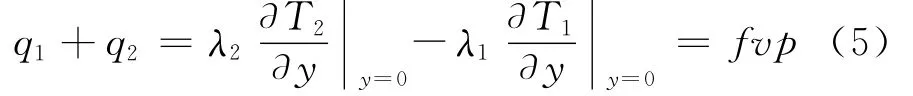
式中：q、T和f分别为热流密度、温度场扰动以及摩擦系数.

根据高等数学知识和方程（2）、（3）和（5），摩擦副的温度场与压力场存在相同形式的扰动，即

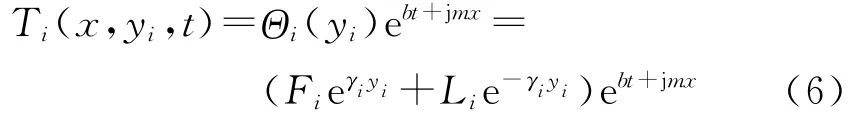
式中：Θi（yi）是关于yi的未知函数；Fi、Li为待求解未知常数；下标i＝1，2，分别表示摩擦片和制动盘.其中，

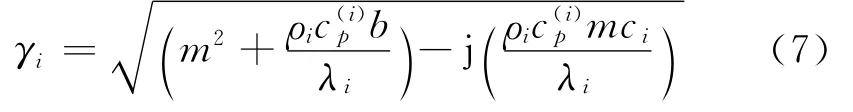
同时，固体温度场应满足瞬态热传导方程，即

为求解满足方程（6）的摩擦片和制动盘温度场扰动式中的未知常数Fi、Li，需要给出相应的4个热边界条件.由文献［4］可知，当热点呈反对称分布时，制动盘中分面上的温度场扰动为零.假设摩擦面完全接触，则对应接触点温度场扰动相同，均为K0ebt＋j mx（K0为任意常数）.对于传统路面及轨道车辆上所装备的盘式制动器，组成摩擦副的零件主要有制动盘、闸片和钢背.钢背一方面可用来固定摩擦片，另一方面可由螺栓连接将摩擦片铰接于制动夹钳上.由于钢背的材料为铸钢，而摩擦片为复合材料，其刚度要远小于钢背.因此，文中假设摩擦片的温度场扰动在钢背和摩擦片的连接处为零.将式（6）代入式（8），结合上述热边界条件，即可确定式（6）中的自定义未知函数Θi（yi），并进一步可得到摩擦片和制动盘的温度场扰动形式分别为

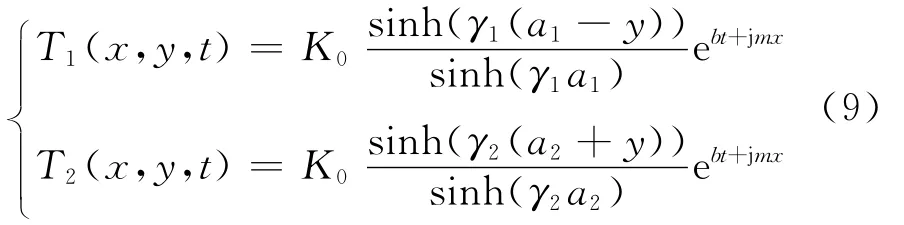
1.3 热弹性应力与变形分析

由于摩擦副间的接触压力和温度场存在扰动，这些扰动会引起材料的热弹性和热应力出现相应扰动.由热弹性力学理论可知，在已知温度场扰动式（9）的前提下，满足由位移表示的二维热弹性平衡非齐次微分方程［4］的特解可通过求解位移势函数ψi得到，其具体形式为

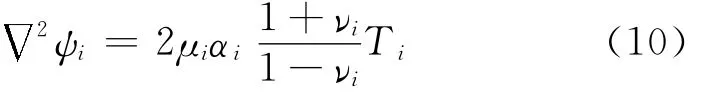
式中：μi、αi和νi分别为材料的剪切模量、线胀系数以及泊松比.

将温度场扰动表达式（9）代入式（10），通过迭代计算和化简后可得到位移势函数ψi分别为由位移势函数ψi可得到对应的热弹性变形u和热应力σ特解分别为

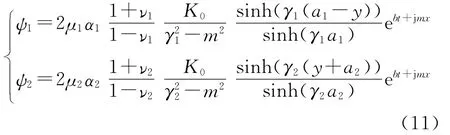
热弹性平衡非齐次微分方程（8）的齐次通解可由Green等［15］解的A和D形式相加得到.文中引入2个调和函数τi和ωi，其形式如下所示：

式中：Bi、Ci、li和Mi为未知常数.根据调和函数可得到对应的热弹性变形和热应力齐次通解为

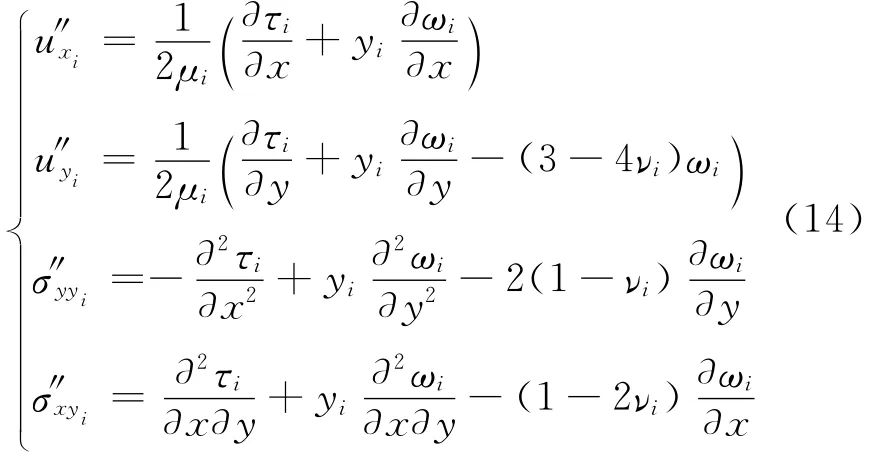
在滑动摩擦过程中引起的总热弹性变形和应力的通解为

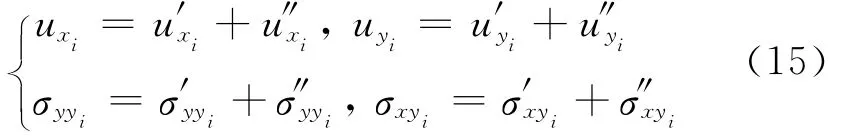
式（15）中的8个未知常数Bi、Ci、li和Mi可由下面的边界条件来确定：

（1）摩擦面上（y＝0），有

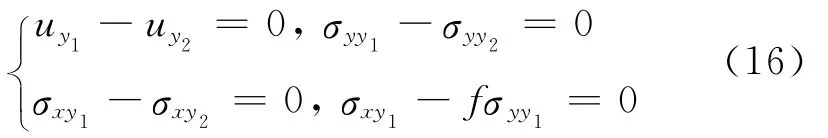
（2）制动盘中分面上（y2＝0），有

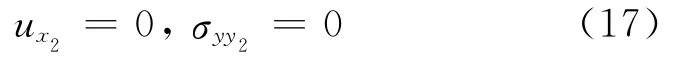
（3）假设与钢背连接处摩擦片背面（y1＝a1）的x和y方向上的位移扰动为零，即

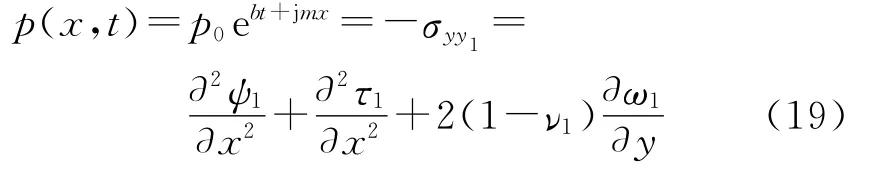
1.4 特征平衡方程

假设在制动过程中，忽略由空气引起的对流换热和辐射换热的影响［2］.由式（2）和（9）可知，当b＞0时，接触压力和温度场扰动均随时间呈指数增长，此时系统处于TEI状态；当b＜0时，系统内的扰动随时间逐渐衰减，系统越趋于稳定；若令b＝0，即为TEI状态的临界速度，是判断系统发生热弹性失稳的标准.将式（2）、（9）和（19）代入式（5），化简后得到

待未知常数Bi、Ci、li和Mi确定后，根据滑动摩擦面（y＝0）上存在的边界条件式（19）来确定接触压力扰动p中的扰动幅值p0，即临界速度

2 结果与分析

国内某条快速城市轨道交通车辆所装备的盘式制动器中摩擦副由HT250制动盘［16］和复合材料摩擦片［17］组成.室温下，两者的材料特性参数如表1所示.表中还给出了另外2种用于制造汽车离合器和制动器中摩擦片的材料：NAO［18］和FGM［19］，其配副均为HT250制动盘.为研究简便，表1中将3种不同摩擦片材料（摩擦片1～3）和HT250制动盘组成的摩擦副分别称为摩擦副系统1、2和3.本文所取的摩擦副结构参数如表2所示，摩擦系数f＝0.32［17］.

表1 室温下不同摩擦副材料参数Tab.1 Material properties of different brake pairs at room temperature

表2 摩擦副的结构参数Tab.2_Structural parameters of brake pair

若令扰动增长系数b＝0，由不同摩擦片材料组成的摩擦副系统的临界速度vcr随扰动频率m的变化关系如图2所示.从图中可以看出，不同摩擦副系统对应的临界速度vcr随扰动频率m均呈先减小后增大的变化规律，每条曲线以下部分为系统的热弹性稳定区，曲线以上部分为热弹性失稳区.不同扰动频率m对应一个临界速度vcr，且系统存在一个发生热弹性失稳时所需的最低临界速度vcr，min，如摩擦副系统3的点O1，对应的扰动频率称为临界扰动频率mcr.图中虚线G1G2和H1H2表示的是在相同临界速度vcr下，摩擦副系统3可受到2个不同扰动频率m的激励.不同摩擦副系统的最低临界速度以及对应的临界扰动频率均不同，且摩擦副系统3发生热弹性失稳时所需的最低临界速度要比另外2种摩擦副系统的高.通过比较表1中3种不同摩擦片材料的特性参数，分析其原因可能是由于复合材料中与温度相关的弹性模量、导热系数以及比定压热容等参数的不同而导致摩擦面发生热弹性变形较小，从而系统变得更稳定.为了验证该结论，文中后续将对复合材料摩擦片的热物理特性参数对系统热弹性失稳的影响做进一步研究.

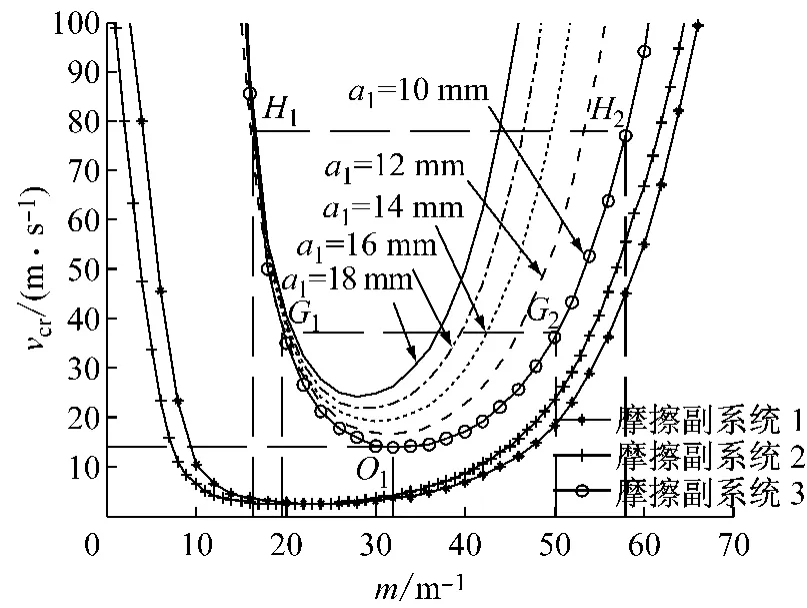
图2 临界速度随扰动频率的变化曲线Fig.2 Change of critical velocity with wave number

保证制动盘厚度2a2＝0.03m不变，图2给出了由不同厚度的摩擦片与制动盘组成的摩擦副系统3的临界速度随扰动频率的变化关系.从图中可以看出，当m≤18m－1时，不同摩擦片厚度对应的临界速度曲线基本重合，但当m＞18m－1时，同一扰动频率对应的临界速度随摩擦片厚度的增加而逐渐增大，即滑动摩擦系统的热弹性稳定性逐渐提高.表3给出了当m＝40m－1时，不同摩擦片厚度所对应的临界速度值及变化关系.从表中可以看出，当摩擦片厚度a1从10mm增加至18mm时，临界速度从17.09 m·s－1增加至49.48m·s－1，且增量不断提高.分析原因主要是由于摩擦片的热容量会随其厚度的增加而增大，在等量摩擦热的作用下，滑动摩擦面上以及y轴方向上（见图1）的温升效应和温度梯度势必会减小.在刚度不变的前提下，引起的热应力也会减小，降低了摩擦面上产生的热弹性变形，使得摩擦面上的温度以及压力分布更加趋于均匀，从而提高了滑动摩擦系统的稳定性.

表3 不同摩擦片厚度对应的临界速度（m＝40m－1）Tab.3 Change of critical velocity with thickness of frictional pad（m＝40m－1）

此外，从图2中还可以看出，随着摩擦片厚度a1的增加，摩擦副系统3的最低临界速度vcr，min逐渐提高，对应的临界扰动频率mcr逐渐减小.表4给出了不同摩擦片厚度a1对应的最低临界速度vcr，min以及临界扰动频率mcr值.从表中可以看出，当摩擦片厚度a1从10mm增加至18mm，增加了80%时，对应临界扰动频率mcr从28.14m－1减小至17.21m－1，而最低临界速度vcr，min则从14.17 m·s－1增加至24.28m·s－1，增加了71.35%.这表明，最低临界速度vcr，min值很大程度上取决于摩擦片厚度a1.若假设给摩擦片厚度a1相同的增量2mm，从表4中可知，虽然最低临界速度保持增加，但增量却逐渐减小，由最初的＋17.22%逐渐降低至＋11.99%.这表明，滑动摩擦系统的热弹性稳定性虽可以通过增加摩擦片厚度来得到提高，但摩擦片厚度增加到一定程度后，其对系统稳定性的影响逐渐越小.此外，过多增加摩擦片厚度，不但造成摩擦副结构异常庞大，且还会增加车辆的簧下质量，也不利于列车的行驶稳定性.比较文献［12］，若在建立制动器TEI数学模型的过程中仍不考虑摩擦片厚度的影响，而直接采用一半无限大平面来替代，根据图2和表4的计算结果可知，由无限大厚度摩擦片计算得到的最低临界速度值要比具有固定摩擦片厚度的高，影响了计算结果的准确性.而实际上，车辆变速箱中所装备的离合器虽由多块金属盘和摩擦片组成，但两者均有一定的厚度.因此，若忽略摩擦片厚度带来的影响会与实际情况不符.

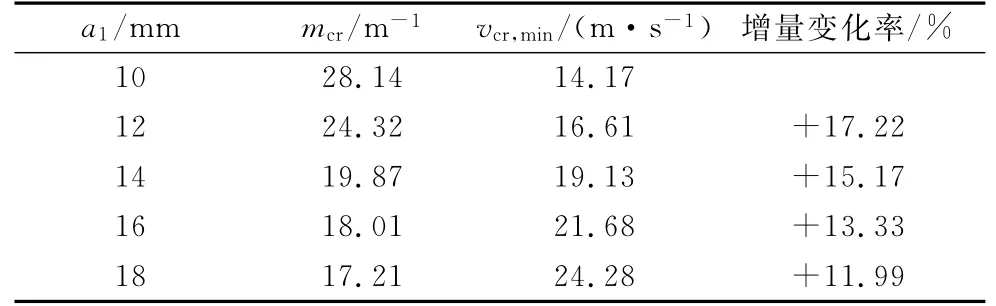
表4 不同摩擦片厚度对应的最低临界速度Tab.4 Change of minimum critical velocity with thinkness of frictional pad

若令扰动增长系数b＝0，得到摩擦副系统3中摩擦片和制动盘内迁移速度c1和c2随扰动频率m的变化关系，如图3和4所示.从图中可以看出，在log坐标系内，随着扰动频率m的增加，扰动在摩擦片内的迁移速度c1呈先减小后增加的变化趋势，而扰动迁移速度c2与c1的变化正好相反，两者均在扰动频率m≈31.65m－1处达到峰值，这与图3所示的摩擦副系统3的最低临界速度所对应的临界扰动频率基本一致.若取m＝50m－1，对应的扰动在摩擦片和制动盘内的迁移速度分别为c1＝39.51m·s－1，c2＝－0.04m·s－1.而由图3可知，当m＝50m－1时，对应的临界速度vcr＝39.55m·s－1.可见，扰动在摩擦片内的迁移速度与临界速度基本一致.此外，扰动在制动盘内的迁移速度很小，几乎为零.因此，可得出热点更倾向于出现在制动盘的摩擦面上.

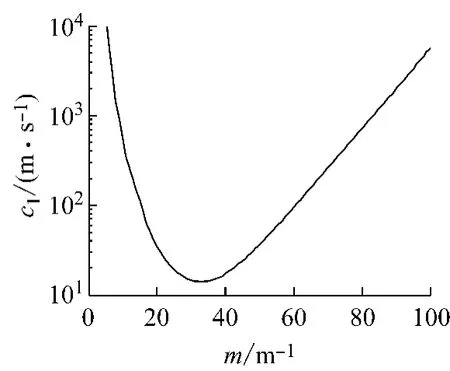
图3 扰动迁移速度c1随扰动频率m的变化曲线Fig.3 Change of velocity of perturbation c1with wave number m

若令扰动增长系数b＝0，扰动频率m＝50m－1，扰动在摩擦片和制动盘内的迁移速度ci随滑动速度v的变化关系如图5所示.可以看出，扰动迁移速度c1和c2的绝对值均随滑动速度v近似呈线性增加的变化趋势，2条直线的斜率分别近似于1和－1.扰动在制动盘层内的扰动速度c2值很小，几乎为零，该结论与图3一致，进而可得到c1≈v.通过比较材料的热物理特性参数可知：扰动在具有高导热系数材料内的迁移速度很慢，几乎为静止.

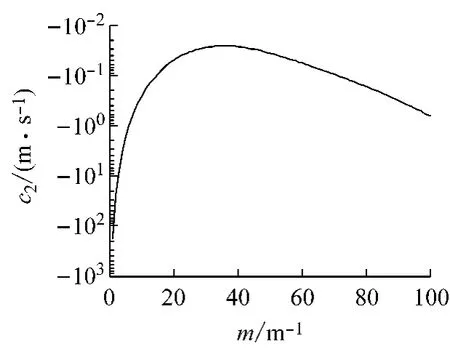
图4 扰动迁移速度c2随扰动频率m的变化曲线Fig.4 Change of velocity of perturbation c2with wave number m

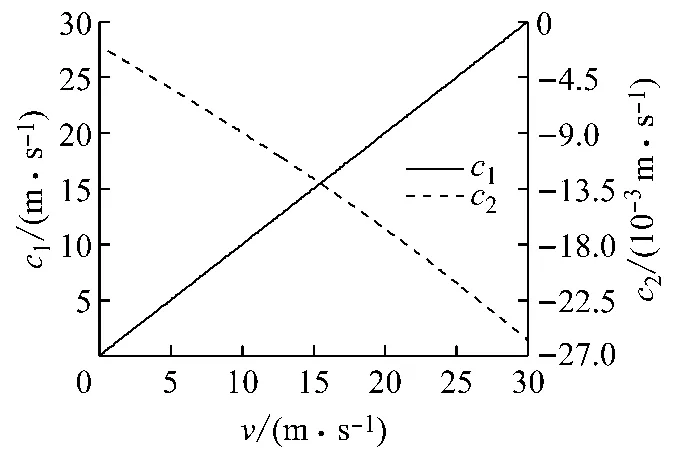
图5 扰动速度ci随滑动速度v的变化曲线Fig.5 Change of velocity of perturbation ciwith sliding velocity v

文献［17］给出了图2中G1、G2、H1和H24个扰动频率所对应的扰动增长系数随滑动速度的变化曲线，并指出：在TEI区域内，若不同扰动频率具有相同的临界速度，扰动频率越低，对系统发生TEI的影响越小.因此，本文在后续对摩擦副系统3TEI的影响研究均基于图3中临界扰动频率mcr（O1）的右侧区域.假设N个热点均匀分布在制动盘滑动摩擦面当量摩擦半径rμ［17］的圆周方向上，则扰动频率m、波长β与热点数N存在如下关系：

式中：r1、r2分别为制动盘的内、外半径.

保持其他参数不变，改变摩擦片的弹性模量E1，不同热点数N对应的临界速度vcr的变化如图6和表5所示.从图中可以看出：在log坐标系内，临界速度vcr随热点数N近似呈线性增加的变化趋势.两者呈线性关系的原因是：从图3中可看出，临界速度随扰动频率呈指数增长的变化规律，而Matlab中的log又是以指数e为底的函数.因此，取对数后，临界速度则随热点数呈线性变化的规律.随着热点数N的增加，临界速度逐渐增大的原因是：在盘面呈周向分布的热点的扰动频率m会随热点数N的增加而增大，系统需要在摩擦面上产生更多的热量来激发更大的热弹性变形的发生，因此系统的临界速度会逐渐提高.随着摩擦片弹性模量E1的增加，不同热点数N对应的临界速度逐渐减小.主要原因是，摩擦材料的弹性模量是衡量其抵抗弹性变形能力大小的力度，弹性模量越大，使材料发生一定弹性变形的应力也越大，进而增强了应力场的非均匀性，导致系统的稳定性会随摩擦片弹性模量的增加而逐渐降低.如表5所示，当热点数N＝16时，弹性模量E1的增量相同，临界速度vcr的降低量却逐渐减小.这表明当摩擦片的弹性模量增大到一定程度时，对系统发生TEI的影响逐渐减小，会被其他因素，如厚度、导热系数以及比定压热容等因素取代.

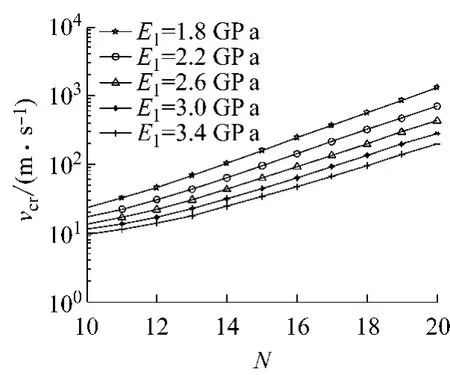
图6 不同摩擦片弹性模量E1对临界速度vcr的影响Fig.6 Effect of frictional pad’s elastic modulus E1on critical speed vcr

表5 摩擦片弹性模量与临界速度（N＝16）Tab.5 Changes of elastic modulus of frictional pad with critical speed（N＝16）

导热系数是指热流密度与温度梯度的比值，是表征材料导热性的参数.材料的导热性会影响摩擦生成的热量在摩擦副之间的分配，进而影响到摩擦副的温度分布及热应力.图7和表6分别给出了摩擦片导热系数λ1对系统临界速度vcr的影响.从图7中可以看出，当导热系数λ1增大后，临界速度vcr明显提高.由式（1）可知：当导热系数λ1增大时，热载荷分配系数δ值逐渐降低，即被制动盘吸收的热载荷逐渐减小，制动盘的温升逐渐降低，相应的热弹性变形也减小，进而降低了制动盘表面出现热点的可能性，系统变得越来越稳定.从表6中可以看出，在摩擦片导热系数增量相同的情况下，系统临界速度的增量越来越高.但这里也需要指出的是，在摩擦制动器的设计过程中，过多增大摩擦片的导热系数λ1，会导致摩擦片的温升过高，易出现磨损、热蚀和摩擦系数变得不稳定等缺陷，影响整个制动器的使用寿命，因此在制动器的设计过程中要综合考虑该因素带来的影响.

图7 摩擦片导热系数λ1对临界速度vcr的影响Fig.7 Effect of frictional pad’s thermal conductivity λ1on critical speed vcr

表6 摩擦片导热系数与临界速度（N＝16）Tab.6 Changes of thermal conductivity of frictional pad with critical speed（N＝16）

图8给出了滑动摩擦系统的临界速度随摩擦片比定压热容的变化关系.可以看出，随着比定压热容的增加，临界速度v逐渐增大.分析原因主要有

cr2个方面：一方面依据式（1），可推出制动过程中经热传导至摩擦片内部的热载荷会随其比定压热容的增加而减少；另一方面，依据比定压热容的定义，即为单位质量的某种物质，在温度升高吸收的热量与其质量和升高的温度乘积之比.由于被摩擦片吸收的热量以及质量保持不变，若要增加比定压热容，则摩擦片的末温度就要降低，即摩擦片比定压热容的增加会引起其在制动过程中的温升减小.因此可以得出：滑动摩擦系统的TEI会随摩擦片比定压热容的增加而逐渐提高.

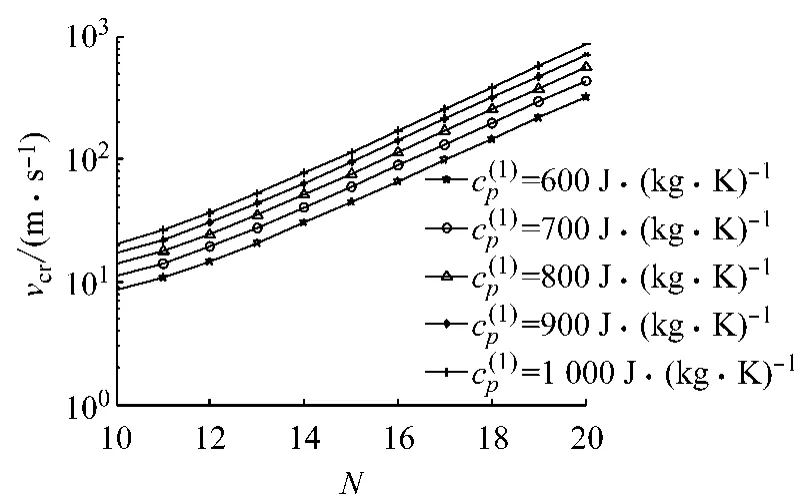
图8 摩擦片比热容c（1）p对临界速度vcr的影响Fig.8 Effect of frictional pad’s specific heat c（1）pon critical speed vcr

线胀系数是指单位温度变化所导致的体积变化.在相同的温升条件下，线胀系数越大，引起的热变形也越大.摩擦片不同线胀系数α1对应的临界速度vcr随热点数N的变化曲线如图9和表7和所示.从图中可以看出，临界速度vcr随线胀系数α1的变化很小.从表7中可以看出，当线胀系数α1从6×10－6K－1增加至9×10－6K－1，增加了50%时，对应的临界速度从128.66m·s－1增加至137.41m·s－1，增加了仅6.8%.分析其原因主要是由于摩擦片的导热系数要小于制动盘，制动过程中绝对大部分热量经热传导作用被制动盘吸收，仅有少部分热量进入摩擦片，所以滑动摩擦系统的临界速度对摩擦片线胀系数的改变不敏感.

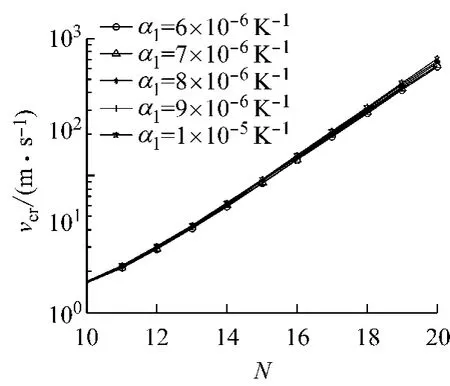
图9 摩擦片线胀系数α1对临界速度vcr的影响Fig.9 Effect of frictional pad’s thermal expansion coefficientα1on critical speed vcr

表7 摩擦片线胀系数与临界速度Tab.7 Changes of thermal expansion coefficient of frictional pad with critical speed

3 间歇接触TEI模型

本文第1、2节的研究是基于组成摩擦副系统的摩擦片和制动盘均为轴对称结构.如前所述，对于传统路面及轨道车辆上所装备的盘式制动器，组成摩擦副的零件主要有制动盘、闸片和钢背，如图10a所示.在制动过程中，摩擦片和制动盘并非连续接触.此时，摩擦片并不具有轴对称结构.因此，若要考虑摩擦片有限周向接触弧长对热弹性失稳的影响，须建立如图10b所示的间歇接触TEI模型.

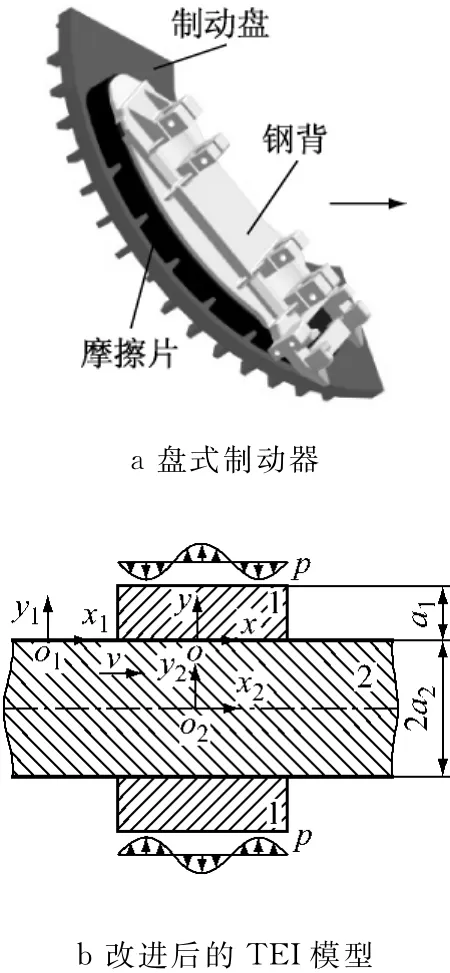
图10 间歇接触TEI数学模型Fig.10 TEI model of intermittent contact

目前还没有精确的解析法来求解间歇接触摩擦制动器的热弹性失稳问题［4，20］.Lee等［4］基于列车的制动时间要远大于摩擦副旋转一周需要的时间，将摩擦生成的热量在制动盘和摩擦片重新分配来处理间歇接触问题.Ayala等［21］在文献［4］的研究基础上指出，只要系统的傅里叶系数F0＜0.1，采用解析法得到的结果误差仅有1%.Hartsock等［20］则提出将摩擦产生热量除以盘、片的接触弧长比来近似处理摩擦副的间歇接触问题，即将特征平衡方程（4）做一定的修正，可得到

式中：U为摩擦副接触弧长比；φ为摩擦片包络角.

轴对称结构摩擦副（U＝1）和间接接触摩擦副（U＝4）系统的临界速度变化如图13所示.可以看出，在log坐标系内，若考虑摩擦片周向接触弧长的影响，系统的临界速度急剧增加.分析原因主要是由于式（24）确定的被摩擦副吸收的热量相对于轴对称结构摩擦副减小了U倍，很大程度上降低了制动盘和摩擦片在制动过程中的温升效应，进而导致热变形和热应力都相应减小.此外，由于摩擦片和制动盘间歇接触，盘面会周期性地经历加热、对流冷却和再加热的过程，温升效应也会降低，因此系统的稳定性也会得到很大提高.

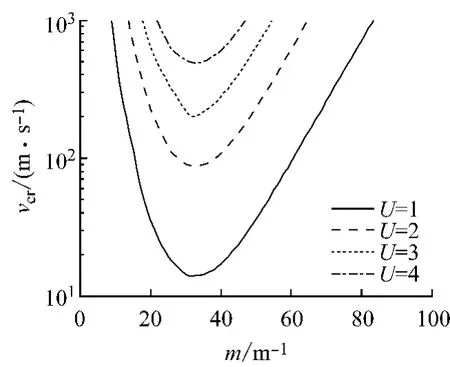
图11 摩擦片有限接触弧长对临界速度vcr的影响Fig.11 Effect of frictional pad’s finite contact length on critical speed vcr

4 结论

（1）不同摩擦副系统均存在一标志其进入热弹性失稳状态的最低临界速度.摩擦片厚度越大，最低临界速度越高，临界扰动频率越提前.

（2）扰动在摩擦片和滑动层内的迁移速度随扰动频率呈相反的变化趋势.扰动在具有较高导热系数的滑动层内速度几乎为零，而在摩擦层内的扰动速度几乎等于滑动层的相对运动速度.增加摩擦片的导热系数、比定压热容和减小弹性模量均可提高滑动摩擦系统的稳定性.

（3）间歇接触摩擦副系统的稳定性要比轴对称结构摩擦副的高.在制动器和离合器的设计过程中，在保证制动性能的前提下，合理选择摩擦片材料对系统的临界速度具有重要影响.

［1］孟德建，张立军，阮丞，等.摩擦引起的制动器热点问题综述［J］.同济大学学报：自然科学版，2014，42（8）：1203.MENG Dejian，ZHANG Lijun，RUAN Cheng，et al.Literature survey of friction－induced hot spots in brakes［J］.Journal ofTongji University：Natural Science，2014，42（8）：1203.

［2］Yi Y B，Bendawi A.Effect of convective cooling on frictionally excited thermoelastic instability［J］.Wear，2012，296（1）：583.

［3］MAO Jiajia，KE Liaoliang，WANG Yuesheng.Thermoelastic contact instability of a functionally graded layer［J］.International Journal of Solids and Structures，2014，51（23／24）：3962.

［4］Lee K J，Barber J R.Frictionally excited thermoelastic instability in automotive disk brakes［J］.Journal of Tribology，1993，115（4）：607.

［5］Burton R A，Nerlikar V，Kilaparti S R.Thermoelastic instability in a seal－like configuration［J］.Wear，1973，24（2）：177.

［6］Zagrodzki P，Truncone S A.Generation of hot spots in a wet multidisk clutch during short－term engagement［J］.Wear，2003，254（5／6）：474.

［7］Ostermeyer G P，Graf M.Influence of wear on thermoelastic instabilities in automotive brakes［J］.Wear，2013，308（1／2）：113.

［8］DU Shuqin，Zagrodzki P，Barber J.R，et al.Finite element analysis of frictionally excited thermoelastic instability［J］.Journal of Thermal Stresses，1997，20（2）：185.

［9］ZHAO Jiaxin，MA Biao，LI Heyan，et al.The effect of lubrication film thickness on the thermoelastic instability under fluid lubrication condition［J］.Wear，2013，303（1／2）：146.

［10］Painer S，Dufrénoy P，Weichert D.An experimental investigation of hot spots in railway disc brakes［J］.Wear，2004，256（7／8）：764.

［11］Kasem H，Brunel J F，Dufrénoy P，et al.Thermal levels and subsurface damage induced by the occurrence of hot spots during high－energy braking［J］.Wear，2011，270（5）：355.

［12］赵家昕，马彪，李和言，等.车辆离合器局部高温区成因及影响因素理论研究［J］.北京理工大学学报，2013，33（12）：1234.ZHAO Jiaxin，MA Biao，LI Heyan，et al.Research on the hot spots and thermoelastic instability of automotive clutches［J］.Transactions of Beijing Institute of Technology，2013，33 （12）：1234.

［13］Talati F，Jalalifar S.Analysis of heat conduction in a disk brake system［J］.Heat and Mass Transfer，2009，45（8）：1047.

［14］李明.高速列车制动盘热-机耦合数值模拟［D］.成都：西南交通大学，2007.LI Ming.Coupled thermo－mechanical numerical simulation of brake discs for high－speed trains［D］.Chengdu：Southwest Jiaotong University，2007.

［15］Green A E，Zerna W.Theoretical Elasticity［M］.Oxford：Oxford University Press，1968.

［16］余为高.通风盘式制动器热-机耦合仿真分析及寿命预测［D］.广州：华南理工大学，2010.YU Weigao.Thermal－mechanical coupled simulation and life prediction for a ventilated disc brake［D］.Guangzhou：South China University of Technology，2010.

［17］夏德茂，奚鹰，朱文翔，等.二维轴对称摩擦制动器瞬态热弹性失稳的研究［J］.机械工程学报，2015，51（20）：144.XIA Demao，XI Ying，ZHU Wenxiang，et al.Transient frictionally excited thermoelastic instability analysis of two dimensional axisymmetric friction brake［J］.Journal of Mechanical Engineering，2015，51（20）：144.

［18］Decuzzi P，Ciaverella M，Monno G.Frictionally excited thermoelastic instability in multi－disk clutches and brakes［J］.Journal of Tribology，2001，123（4）：865.

［19］Lee S W，Jang Y H.Effect of functionally graded material on frictionally excited thermoelastic instability［J］.Wear，2009，266（1）：139.

［20］Hartsock D L，Fash J W.Effect of pad／caliper stiffness，pad thickness，and pad length on thermoelastic instability in disk brakes［J］.Journal of Tribology，2000，122（3）：511.

［21］Ayala J R R，Lee K J，Rahman M，et al.Effect of intermittent contact on the stability of thermoelastic sliding contact［J］.Journal of Tribology，1996，118（1）：102.

Effect of Material Properties and Structure of Frictional Pad on Thermoelastic Instability of Disc Brake

XIA Demao，XI Ying，ZHU Wenxiang，HUA Binbin
（School of Mechanical Engineering，Tongji University，Shanghai 201804，China）

A mathematical model on thermoelastic instability （TEI）of two dimensional disc brake was built.Change rules of critical speed，growth rate of perturbation and its migration velocity in metal disk and frictional pad were respectively resolved by utilizing perturbation method with the assumption that hot spots were antisymmetrically distributed on frictional surfaces.Then，the effects of frictional pad’s thickness，material properties and finite contact length on critical speed were analyzed and compared.The results show that，critical speed will decrease firstly and then grow again with wave number and there is an opposite trend of migration velocity in brake disk and frictional pad.Meanwhile，it is almost zero in metal disk with higher thermal conductivity.The stability of sliding frictional system can be enhanced by increasing the thickness，thermal conductivity and specific heat of the frictional pad.

disc brake；thermoelastic instability（TEI）；growth rate of perturbation；critical speed；wave number

U463.51

A

0253－374X（2016）01－0119－09

10.11908／j.issn.0253－374x.2016.01.018

2014-11-05

国家留学基金（201406260074）；国家自然科学基金（61004077）

夏德茂（1986—），男，博士生，主要研究方向为制动器和离合器滑动摩擦基础理论.E－mail：demaoxia＠gmail.com

奚 鹰（1957—），男，教授，博士生导师，工学博士，主要研究方向为大型复杂机械系统中关键技术及理论.

E－mail：yingxi＠tongji.edu.cn