机械变速器齿轮敲击现象建模及其影响因素

吴虎威，吴光强，2（.同济大学汽车学院，上海20804；2.东京大学生产技术研究所，东京53 8505）



机械变速器齿轮敲击现象建模及其影响因素

吴虎威1，吴光强1，2
（1.同济大学汽车学院，上海201804；2.东京大学生产技术研究所，东京153 8505）

利用车辆基本参数和实车传动系统各部件的等效转动惯量、扭转刚度和阻尼扭转特性参数，建立了包含LuGre轮胎模型在内的传动系统非线性扭转振动和车辆纵向平移运动耦合模型.利用耦合模型再现了车辆处于一挡加速工况下各非承载齿轮对的敲击情况，并分析了各非承载齿轮对敲击强度的主要影响因素.结果表明，合理设计各挡位齿轮对齿侧间隙和等效转动惯量大小可有效抑制机械变速器齿轮敲击现象.

LuGre轮胎模型；非线性扭转振动；耦合模型；齿侧间隙；等效转动惯量

随着汽车工业的蓬勃发展，用户对于汽车乘坐的舒适性要求越来越高，汽车振动噪声品质越来越受到重视.变速器作为汽车动力传动系统的重要组

国内外已有关于变速器齿轮敲击问题的研究成果.在仿真建模方面，Wang等［2－3］较早利用基于集中质量的系统动力学方法针对变速器系统建模.模型中包括承载齿轮对和非承载齿轮对，将单个齿轮等效为集中转动惯量，齿轮间轴段等效为扭转刚度和扭转阻尼，仿真分析了变速器系统不同非承载齿轮对敲击强度.对于传动系统模型进行较大简化，将半轴、轮胎和整车质量等效为较大的单一集中转动惯量，并且假定非承载齿轮对所受阻滞力矩为定值，这与实际情况不符.Robinette等［4－5］针对装有某款手动变速器的传动系统，采用集中质量的系统动力学建模方法，建立了空套齿轮的阻滞力矩力学模型，并通过与仿真模型对应的试验装置验证了仿真模型的有效性.但该模型利用时域内阶梯型递增的转矩输入模拟整个传动系统的动力输入，而且模型中未考虑轮胎特性和整车平动质量，无法真实还原实车在特定工况下的敲击现象.马小英等［6］利用AVL－Timing Drive商业软件搭建变速器系统模型，在齿轮阻滞力矩中考虑搅油损失力矩和轴承摩擦力矩，仿真分析了变速器在怠速工况、五档同步器不同安装位置（输入轴或者输出轴）下各挡位齿轮对啮合力大小，提出五档同步器安装在输入轴上可减小怠速工况下敲击噪声，但未能对齿轮敲击强度主要影响因素进行系统分析.

本文在前人研究工作的基础之上，采用基于集中质量的系统动力学建模方法，利用车辆基本参数和传动系统各部件的等效转动惯量、扭转刚度和阻尼扭转振动特性参数，建立了传动系统非线性扭转振动和车辆纵向受力耦合模型.利用该耦合模型，再现了变速器工作在一挡工况时各非承载齿轮对齿轮敲击现象，并探讨了非承载齿轮对齿侧间隙大小和被动齿轮等效转动惯量大小对敲击强度的影响规律，为进一步研究齿轮敲击现象奠定了理论基础.

1 动力传动系统部件建模

1.1 发动机建模

在动力传动系统中，发动机是系统主要激励源.对于四缸四冲程发动机而言，发动机不平衡往复惯性力及气体压力的点火阶次造成发动机输出转矩波动.发动机输出力矩Te为平均输出力矩Tm和波动力矩Tp之和［7］，如下所示：

式中：Tpn为n次谐波分量的幅值，N·m；φn为n次谐波分量的相位，rad；N为建模中考虑的谐波分量的个数，一般取N＝5；t为时间，s；ωe为发动机曲轴转动角频率，rad·s－1；ωp为四缸四冲程发动机点火频率，rad·s－1.

1.2 离合器扭转减振器特性建模

离合器扭转减振器作为动力传动系统的重要部件，用来避免车辆传动系统共振和缓和所受的冲击载荷，其结构原理如图1所示.当离合器主、从动摩擦盘完全接合后，传动系统输入扭矩波动或者负载力矩变化时，从动盘体和从动盘毂之间将产生相对往复摆动，依靠两者之间减振器弹簧的弹性和阻尼特性改变传动系统扭转振动特性，消耗扭转振动能量.

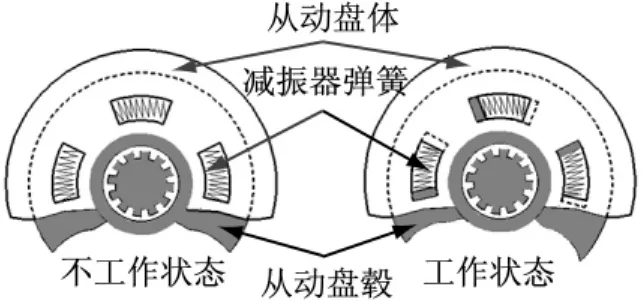
图1 扭转减振器结构原理图Fig.1 Schematic diagram of torsional vibration damper

变速器齿轮敲击属于动力传动系统扭转振动范畴，对于实车出现变速器齿轮敲击现象，多通过合理调节离合器扭转减振器特性参数实现对变速器齿轮敲击振动噪声的有效控制［8］，因此离合器扭转减振特性的建模至关重要，本文选取实车采用的某款离合器扭转减振器.试验测得的扭转特性数据经过曲线拟合后得到的扭转减振器特性曲线如图2所示［］.

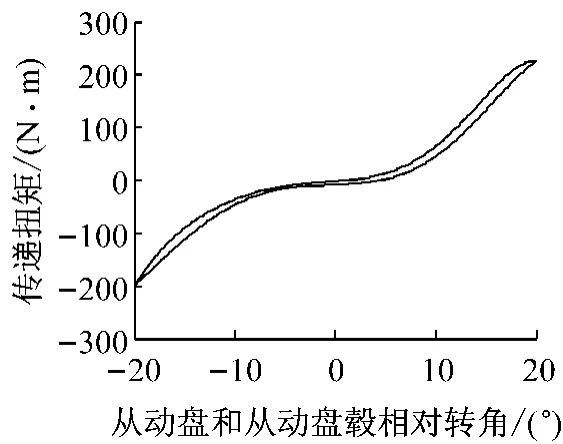
图2 考虑迟滞特性的离合器扭转减振器特性曲线Fig.2 Characteristics curve of clutch torsional vibration damper considering hysteresis characteristics

1.3 考虑齿侧间隙的单对齿轮对建模

对于变速器中任意一对非承载齿轮副的力学模型可简化为如图3所示.小齿轮为敲击主动齿轮，大齿轮为敲击被动齿轮，此处将主动齿轮时域内的运动输入作为单对齿轮系统的激励，因此图中主动齿轮处不施加驱动力矩.单对齿轮系统满足如下力学关系［10］：

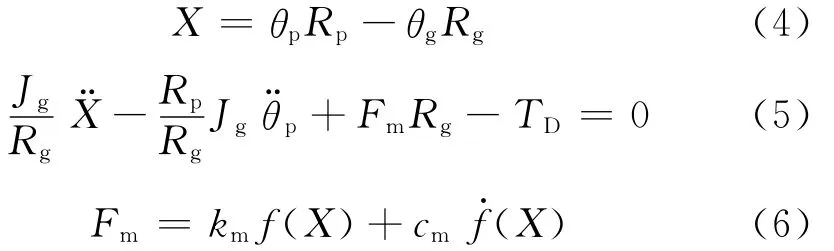
式中：X为沿基圆公切线上的相对位移，m；θp、θg分别为主动齿轮、被动齿轮扭转角度，rad；Rp、Rg分别为主动齿轮、被动齿轮基圆半径，m；Jg为被动齿轮等效转动惯量，kg·m2；km为齿轮副平均啮合刚度，N·m－1；cm为齿轮副平均啮合阻尼，N·s·m－1；TD为敲击被动齿轮所受阻滞力矩，N·m；Fm为齿轮对敲击力，N.其中，齿侧间隙函数f（X）满足如下关系：

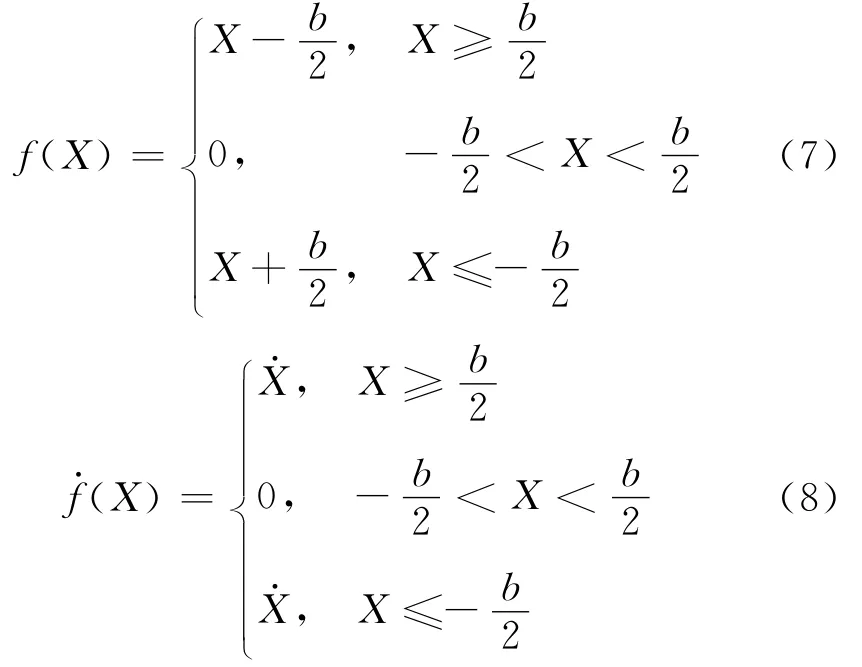
式中：b为齿轮副基圆啮合线上的齿侧间隙，m.

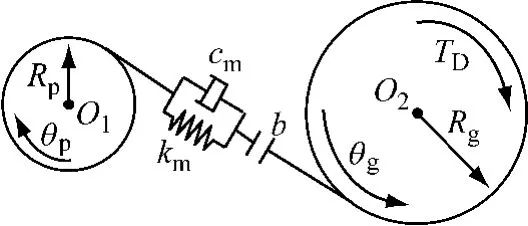
图3 单对齿轮副敲击简化模型Fig.3 Simplified model for rattling gear pair

1.4 空套齿轮拖曳力矩计算

由第1.3节可知，合理计算敲击被动齿轮（空套齿轮）的拖曳力矩可准确反映单对齿轮对敲击力学模型.对于不同挡位的空套齿轮，阻滞力矩TD可能包括滚子轴承损失力矩Trb、油膜剪切损失力矩Tsh和搅油损失力矩Tch.

对于滚子轴承损失力矩Trb，可通过下式进行估计［］：

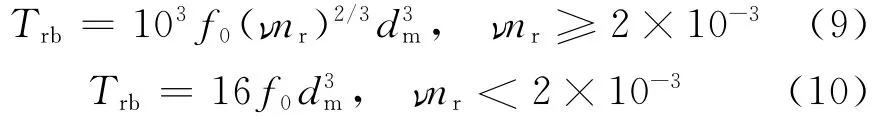
式中：nr为空套齿轮和轴段之间（轴承内外圈）相对转速，r·min－1；dm为轴承内外圈平均直径，m；f0为润滑因子，与润滑油类型和润滑方式有关；ν为润滑油运动黏度，m2·s－1.

油膜剪切损失力矩Tsh产生于空套齿轮与相邻轴段、同步器齿环之间，假设其间油膜流动为库埃特流动方式，则此时油膜剪切损失力矩［5］

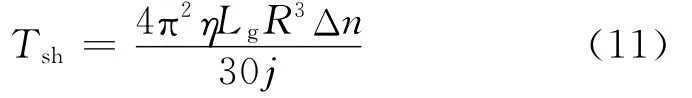
式中：η为润滑油绝对黏度，N·s·m－2；Lg为齿轮长度，m；R为轮齿节圆半径，m；Δn为空套齿轮与相邻轴段、同步器齿环之间的相对转速，r·min－1；j为轴承径向间隙，m.

对于搅油齿轮，其浸油几何关系简图如图4所示，搅油损失力矩［12］

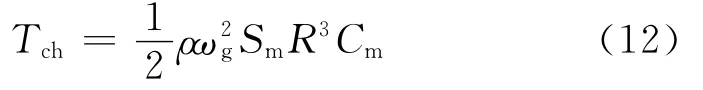
式中：ρ为润滑油密度，kg·m－3；ωg为齿轮旋转角速度，rad·s－1；Sm为齿轮浸油面积，m2；Cm为搅油损失力矩系数.

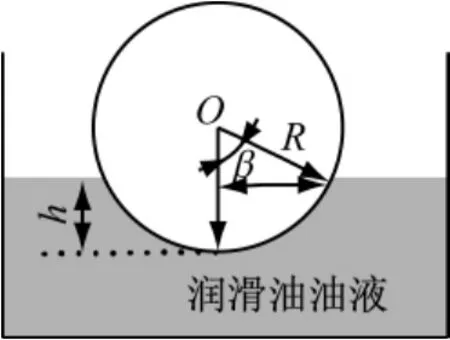
图4 搅油齿轮浸油几何关系简图Fig.4 Geometry relationship of churning oil－immersed gear

齿轮浸油面积Sm包括齿轮外侧面浸油面积Sm，l和齿轮轮齿浸油面积Sm，t之和，即

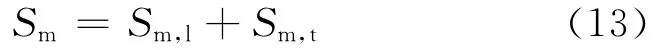
其中，

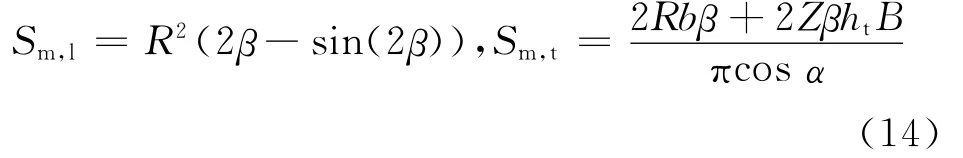
式中：B为齿轮轮齿齿宽，m；ht为齿轮轮齿高度，m；α为齿轮轮齿压力角，rad；Z为齿轮轮齿齿数；h为齿轮浸油深度，m.

对于搅油损失力矩系数C，计算式为m

式中：V0为箱内油体积，L；Fr为弗劳德数；Re为雷诺数；g为重力加速度，m·s－2.

1.5 轴段扭转刚度计算

对于变速器输入、输出轴，按照各挡位齿轮所在位置分成多段，等截面轴段扭转刚度

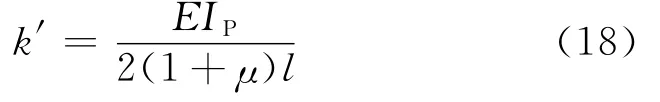
式中：E为轴段材料拉压弹性模量，GPa；IP为轴段截面极惯性矩，m4；l为等截面轴段长度，m；μ为轴段材料泊松比.

实际简化时，将变速器输入轴或者输出轴相邻齿轮间的轴段等效为一个扭转刚度，此时需要等效的轴段多为多截面轴段，此时多截面等效刚度

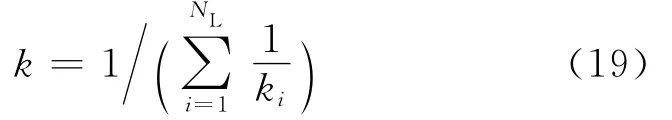
式中：ki为第i个轴段等效刚度，N·m·rad－1；NL为轴段个数.

1.6 基于分布参数的LuGre轮胎模型

本文采用基于分布参数的LuGre轮胎模型，其受力及运动简图如图5所示［13］.

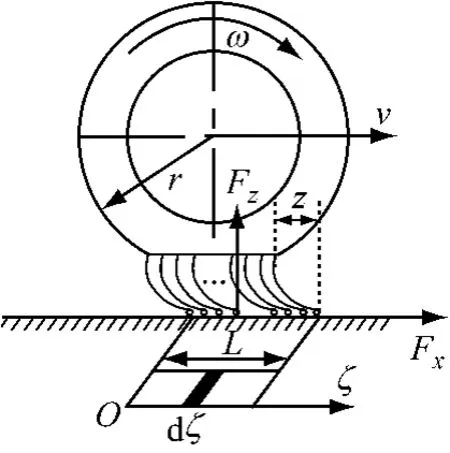
图5 基于分布参数的LuGre轮胎模型Fig.5 LuGre tire model based on distributed parameters

设轮胎上刷毛的平均变形量为z，轮胎相对地面的速度为vr，则毛刷变形的微分方程如下所示［14］：

式中：σ0为纵向等效刚度系数，m－1；σ1为纵向等效阻尼系数，s·m－1；σ2为摩擦面相对黏性阻尼系数，s·m－1；μc为动摩擦因数；μs为静摩擦因数；vs为斯特列贝格相对速度，m·s－1；λ为斯特列贝格效应指数；Fz为地面支持力，N；fn（ζ）为沿轮胎印记纵向压力分布密度函数；n为接地印记沿着ζ轴方向的积分个数；s为轮胎滑移率；r为轮胎滚动半径，m.

2 手动变速器结构形式及建模思路

本文以装备于某车辆的五挡手动变速器为例，变速器主要部件包括输入轴、输出轴、齿轮对和同步器总成等，采用两轴式设计（不包含倒挡轴），包括5个前进挡和1个倒挡，其具体结构形式如图7中所示.当变速器挂入某挡位时，相应的齿轮对传递动力，称为承载齿轮对，其余不传递动力的齿轮对为非承载齿轮对.

手动变速器齿轮敲击现象是动力传动系统扭转振动综合作用的结果，针对装备手动变速器的前置前驱车辆进行动力传动系统建模，其总体建模思路如图6所示，车辆动力传动系统非线性扭转振动分为主线扭转振动和敲击扭转振动.研究学者已经广泛认为空套齿轮的敲击扭转振动对于主线扭转振动的影响很小［2－4］，因此对于各非承载齿轮对，将主线扭转振动上的敲击主动齿轮运动作为敲击扭转振动系统的激励，而不考虑被动齿轮对于主动齿轮运动的影响.

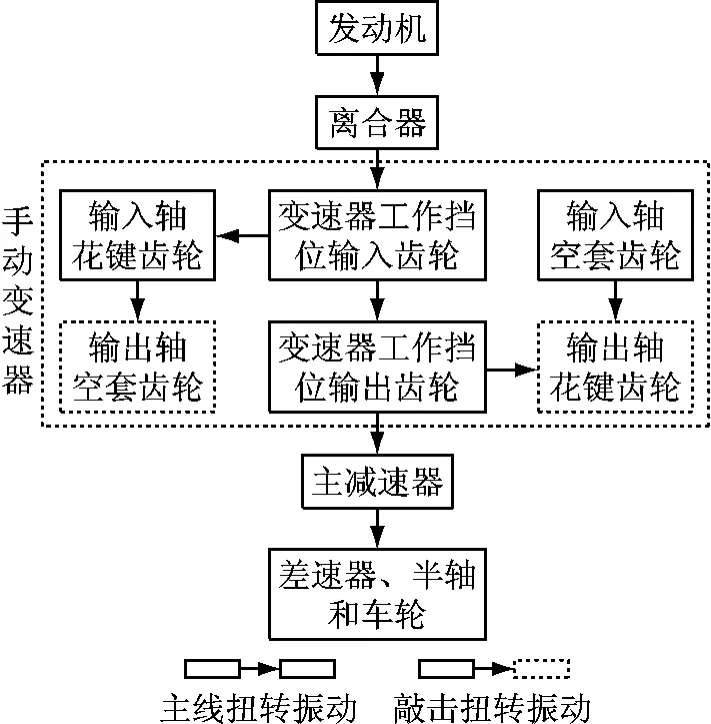
图6 整车动力传动系统建模结构图Fig.6 Structure of vehicle powertrain system modelling

3 传动系统扭转振动力学模型

以车辆行驶在水平道路上、工作挡位为一挡工况，仿真分析手动变速器齿轮敲击现象，建模基于以下假设：

（1）为离合器完全接合后仿真工况，不涉及离合器主、从动盘接合的动力传动过程.对主线扭转振动上的变速器和主减速器内传递动力齿轮对，输入轴二挡齿轮，输出轴三、四、五挡齿轮和同步器总成，忽略搅油损失力矩或者油膜剪切损失力矩对其扭转振动的影响.

（2）忽略变速器输入轴和输出轴轴承、主减速器轴承动态力学特性对于变速器内部齿轮系统扭转振动特性的影响，忽略差速器特性和左右半轴不同扭转刚度对传动系统扭转振动的影响，忽略车辆前后轴左、右车轮垂直载荷的差异，忽略变速器内部部件系统运动带来的润滑油温升.

3.1 主线扭转振动建模

对于主线扭转振动，建立如图7所示的传动系统扭转振动力学模型和如图8所示的整车纵向运动和受力分析模型.

图7 动力传动系统扭转振动模型Fig.7 Driveline torsional vibration model

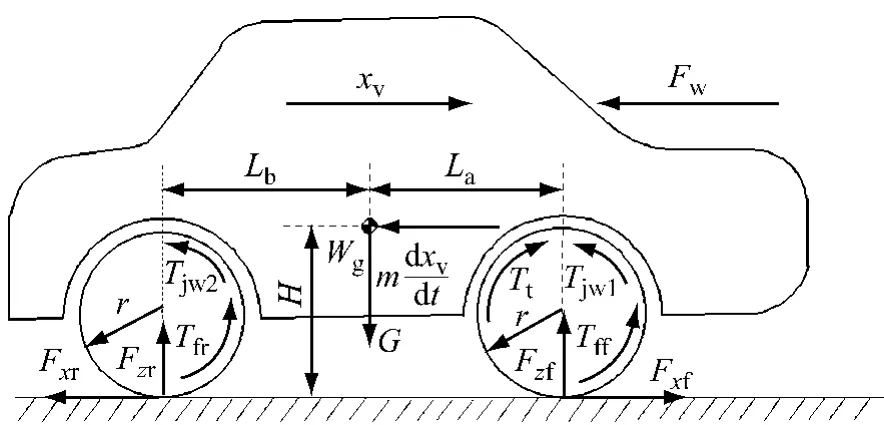
图8 整车纵向运动及受力分析图Fig.8 Vehicle longitudinal motion and force analysis

图7中，Jf为飞轮和离合器主从动摩擦盘转动惯量，kg·m2；JC为离合器从动盘毂转动惯量，kg· m2；JP1～JP5分别为输入轴一～五挡齿轮转动惯量，kg·m2；JG1S1为输出轴一挡齿轮和相应同步器总成转动惯量之和，kg·m2；JP0为输入轴倒挡齿轮转动惯量，kg·m2；JG2～JG5分别为输出轴二～五挡齿轮转动惯量，kg·m2；JS2为三、四挡同步器总成转动惯量，kg·m2；JS3为五挡同步器总成转动惯量，kg· m2；JFD1为主减速器主动齿轮转动惯量，kg·m2；JFD2为主减速器被动齿轮转动惯量，kg·m2；JT为差速器、半轴和车轮的等效转动惯量，kg·m2；k1～k5、c1～c5分别为一～五档齿轮副平均啮合刚度和啮合阻尼，单位分别为N·m－1和N·s·m－1；kf、cf分别为主减速器齿轮副平均啮合刚度和啮合阻尼，单位分别为N·m－1和N·s·m－1；b1～b5分别为一～五挡齿轮副齿侧间隙，m；bf为主减速器齿轮副齿侧间隙，m；TD2～TD5分别为二～五挡被动齿轮所受阻滞力矩，N·m；Tc为离合器扭转减振器传递扭矩，N·m；Tff为轮胎所受地面作用力矩，N·m.

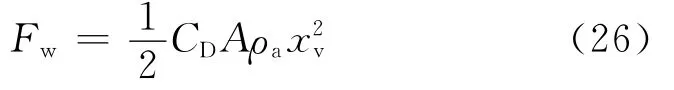
式中：CD为空气阻力系数；A为车辆迎风面积，m2；ρa为空气密度，kg·m－3.

此时，在车辆纵向加速度影响下前、后轴的载荷分配为

根据牛顿第二定律，建立分析变速器齿轮敲击主线扭转振动的数学模型，即

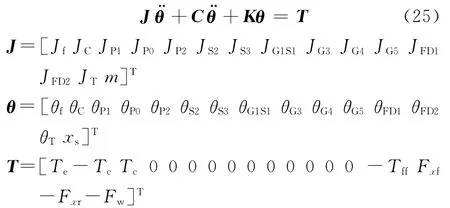
式中：J为惯量矩阵；K为刚度矩阵；C为阻尼矩阵；θ为（角）位移矩阵；T为作用扭矩（力）矩阵；θi（i＝f，C，…，T）为对应转动惯量Ji（i＝f，C，…，T）的角位移，rad；m为车辆整备质量，kg；xs为车辆平移运动位移，m；Fxf为驱动前轮所受地面纵向力，N；Fxr为从动后轮所受地面纵向力，N；Fw为车辆所受空气阻力，N.

图8中，xv为相对速度，在无风时即汽车的行驶速度，m·s－1；Wg为车辆质心；La、Lb分别为车辆质心至前、后轴距离，m；H为车辆质心高度，m；G为车辆整备重力，N；Tt为驱动前轮等效驱动力矩，N· m；Tjw1为驱动前轮惯性力矩，N·m；Fzf为车辆前轴垂直载荷，N；Tjw2为从动后轮惯性力矩，N·m；Tfr为从动后轮受到地面作用力矩，N·m；Fzr为车辆后轴垂直载荷，N.

如图8中所示，车辆所受空气阻力

式中：a为车辆运动加速度，m·s－2；g为重力加速度，m·s－2.

对于驱动前轮进行受力分析，扭转振动方程为

式中：k、c分别为主减速器被动齿轮和半轴、车轮等效转动惯量间的等效扭转刚度和扭转阻尼，单位分别为N·m·rad－1和N·m·s·rad－1；f为滚动阻力系数.

对于从动后轮进行受力分析，扭转振动方程为

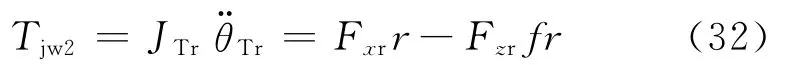
式中：JTr为从动后轮的等效转动惯量，kg·m2；θTr为后轮转动角位移，rad.轮胎模型采用基于分布参数的LuGre模型，地面纵向力Fxf、Fxr利用第1.6节中式（20）～（24）得到.

3.2 敲击扭转振动建模

对于敲击扭转振动，各非承载齿轮对沿基圆公切线上的相对位移大小分别为

式中：RP2、RG2分别为输入、输出轴二挡齿轮基圆半径，m；RP3、RG3分别为输入、输出轴三挡齿轮基圆半径，m；RP4、RG4分别为输入、输出轴四挡齿轮基圆半径，m；RP5、RG5分别为输入、输出轴五挡齿轮基圆半径，m.

对于二挡齿轮副，有

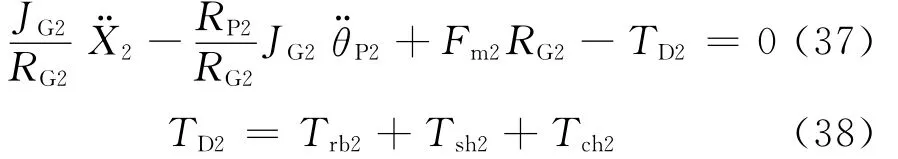
式中：Fm2为二挡齿轮对敲击力，N；Trb2为二挡被动齿轮所受轴承损失力矩，N·m；Tsh2为二挡被动齿轮所受油膜剪切损失力矩，N·m；Tch2为二挡被动齿轮所受搅油损失力矩，N·m.

对于三挡齿轮副，有

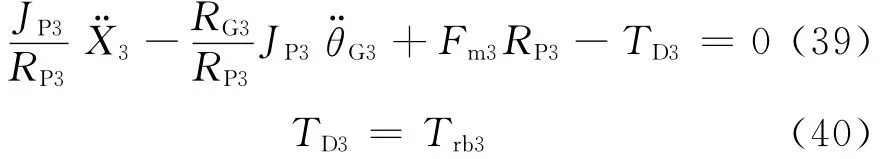
式中：Fm3为三挡齿轮对敲击力，N；Trb3为三挡被动齿轮所受轴承损失力矩，N·m.

对于四挡齿轮副，有

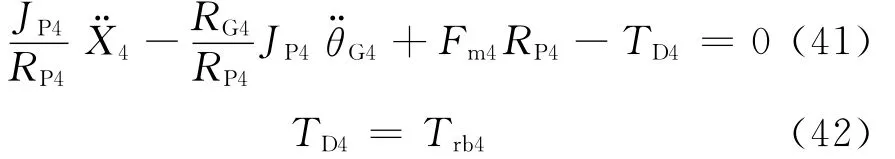
式中：Fm4为四挡齿轮对敲击力，N；Trb4为四挡被动齿轮所受轴承损失力矩，N·m.

对于五挡齿轮副，有

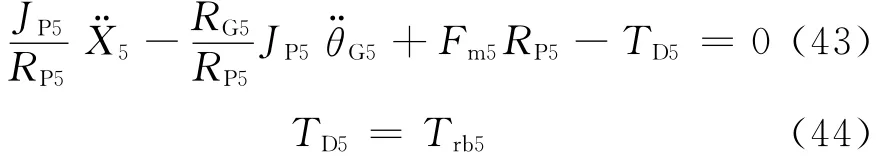
式中：Fm5为五挡齿轮对敲击力，N；Trb5为五挡被动齿轮所受轴承损失力矩，N·m.

4 齿轮敲击结果及其影响因素分析

根据整车厂家反馈，当该款变速器工作在一挡、车辆处于离合器完全接合后起步加速的初始工况下，实车存在较严重的齿轮敲击现象.以下仿真再现该初始工况下各非承载齿轮对敲击现象，并分析主要影响因素对于敲击强度的影响规律.

4.1 实车状态及各挡位敲击情况再现

通过仿真再现实车工况下的发动机飞轮转速和车速变化，分别如图9和10所示，此时对应的各非承载齿轮对敲击力大小如图11所示.

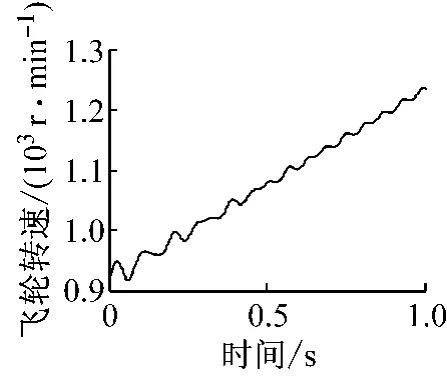
图9 发动机飞轮转速随时间变化曲线Fig.9 Engine flywheel speed curve in time domain

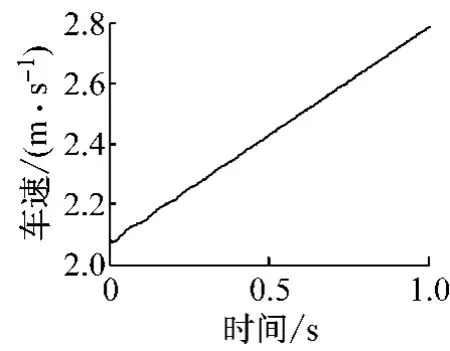
图10 车速随时间变化曲线Fig.10 Vehicle speed curve in time domain

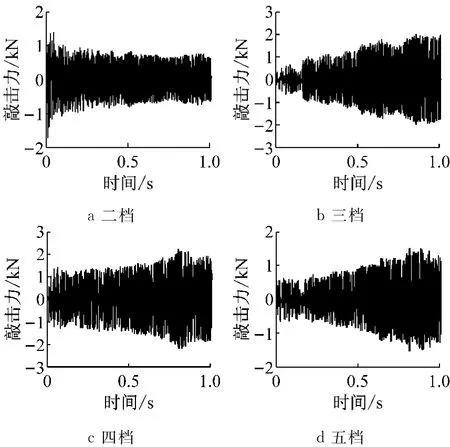
图11 各非承载齿轮对敲击力随时间变化曲线Fig.11 Unloaded gear pairs rattle force in time domain

由图9和10可知，此时发动机转速和车速处于加速过程，发动机飞轮转速存在波动，此转速波动通过离合器扭转减振器传至变速器输入轴而引起变速器内发生齿轮敲击现象.同时，由图11可知，对于二挡齿轮对，随着发动机转速升高，敲击强度有减小趋势，主要是因为二挡被动齿轮随转速升高，搅油阻滞力矩增加，导致敲击强度减小，再现工况末端二挡敲击力大小趋于稳定；对于三挡、四挡和五挡，随着发动机转速升高，敲击强度增大，再现工况末端三挡、四挡和五挡敲击力变化不大.

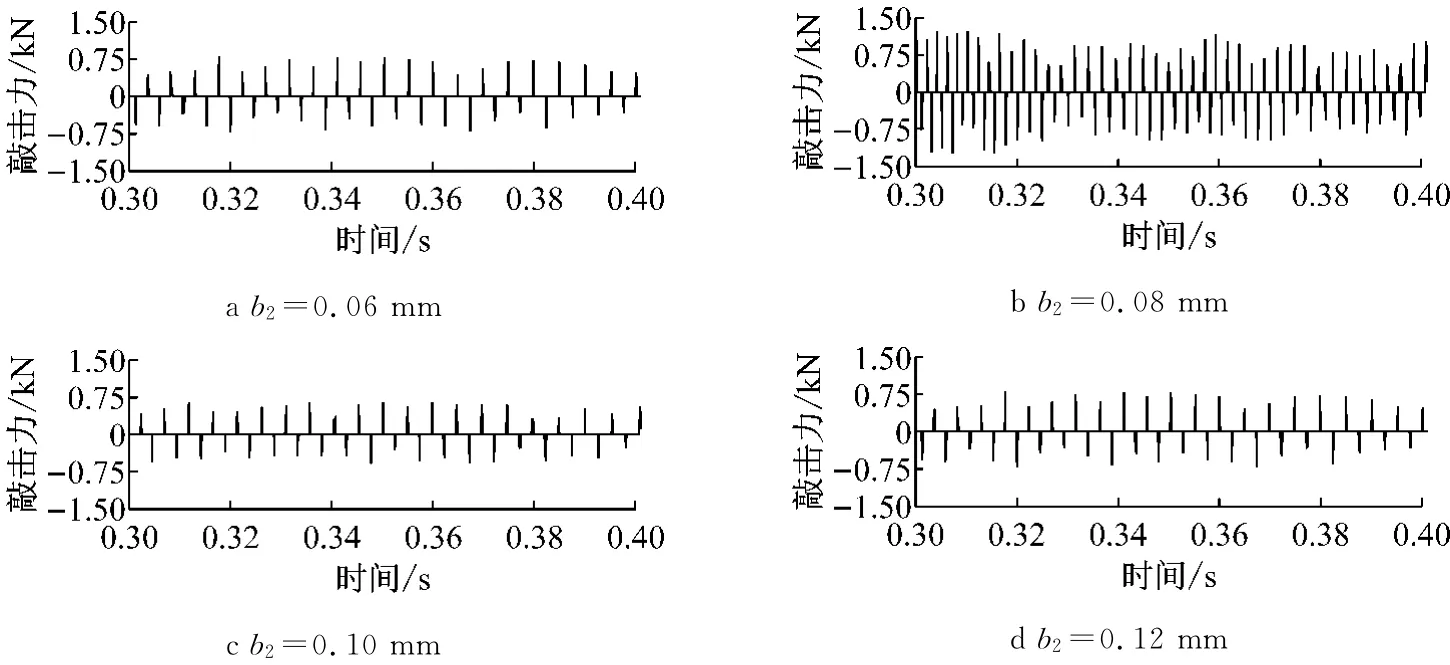
图12 二挡齿轮对间隙影响敲击力图Fig.12 Rattle force of the second gear pair influenced by gear backlash

4.2 齿轮对齿侧间隙大小对于敲击强度影响规律分析

由第1.3节单对齿轮对敲击模型可知，齿侧间隙作为数学模型中主要参数，直接影响敲击结果.由该款手动变速器厂家反馈，各挡位齿轮对齿侧间隙范围为0.06～0.12mm.现分析不同齿侧间隙大小对于各非承载齿轮对敲击强度影响规律，结果如图12～15所示.

图13 三挡齿轮对间隙影响敲击力图Fig.13 Rattle force of the third gear pair influenced by gear backlash

当齿侧间隙b取较小值时，各敲击齿轮对敲击频次较高，结合式（4）～（8）可知，当齿侧间隙越小，敲击被动齿轮一旦与主动齿轮脱啮，敲击被动齿轮齿背就更容易与下一个主动齿轮齿面产生敲击，导致敲击的频次增多.当齿侧间隙由小到大时，敲击力大小总体呈现出先增大后减小的变化趋势，这是因为当齿侧间隙增加时，敲击被动齿轮所受到的阻滞力矩作用时间相对较长，导致敲击前主被动齿轮相对速度增大，敲击力反而增大，当齿侧间隙继续增加时，阻滞力矩作用时间更长，敲击被动齿轮未能发生齿背敲击而继续发生齿面敲击.三挡较四挡、五挡轮齿敲击的频次高，这是因为在齿侧间隙相同的情况下，变速器处于一挡工况时，三挡、四挡和五挡角速度大小基本一致，齿轮对数多的三挡齿轮产生敲击的可能性越大.通过以上分析可知，合理设置各挡位齿侧间隙对于有效抑制齿轮敲击现象具有至关重要的作用，但是一旦实车工况下出现敲击现象，变速器内其他部件参数已经确定，很难调整齿侧间隙以抑制敲击现象，因此应在变速器正向设计中考虑多方 面因素确定合适的各挡位齿侧间隙大小.

图14 四挡齿轮对间隙影响敲击力图Fig.14 Rattle force of the fourth gear pair influenced by gear backlash

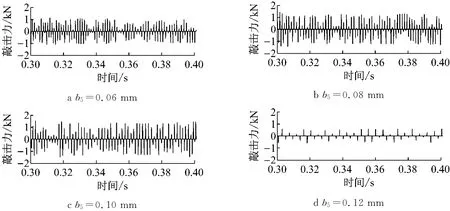
图15 五挡齿轮对间隙影响敲击力图Fig.15 Rattle force of the fifth gear pair influenced by gear backlash

4.3 非承载齿轮转动惯量对于敲击强度影响规律分析

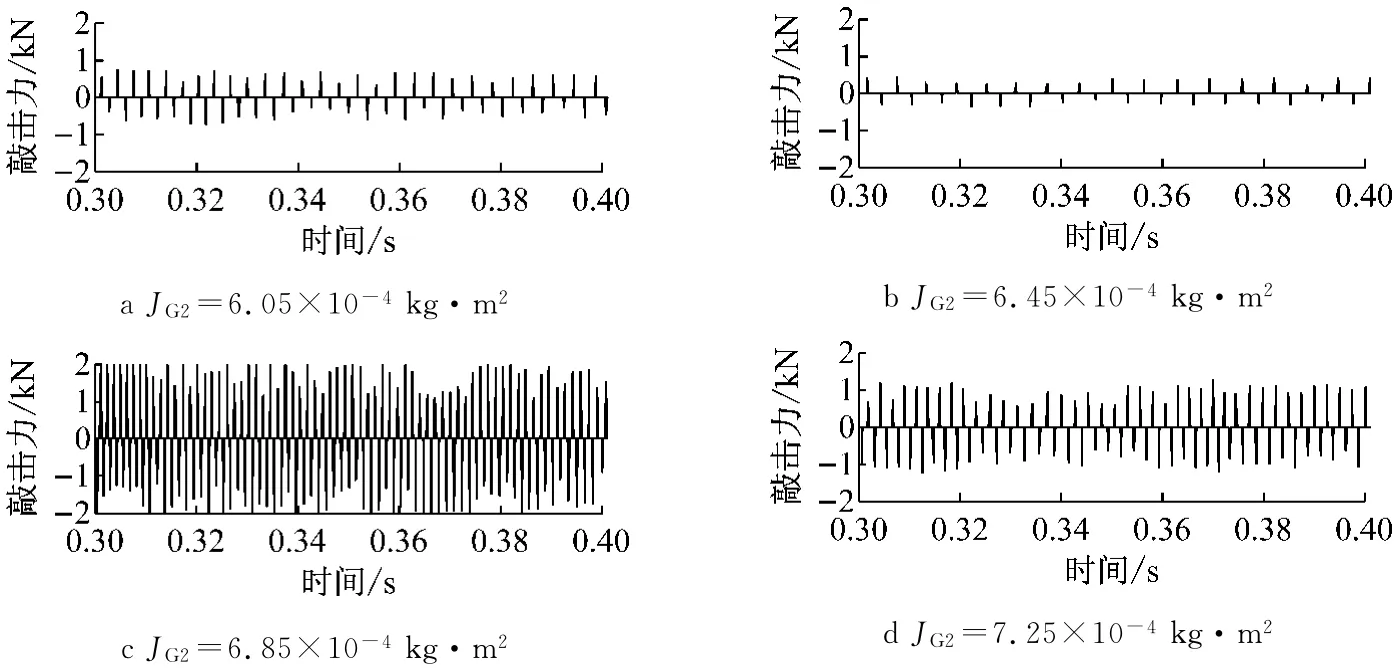
图16 二挡被动齿轮转动惯量影响敲击力图Fig.16 Rattle force of the second gear pair influenced by driven gear torsional inertia

由第1.3节单对齿轮对敲击模型可知，被动齿轮转动惯量作为数学模型中主要参数，也可直接影响敲击结果.以下分析非承载齿轮对被动齿轮转动惯量大小对于敲击强度的影响规律，结果如图16～19所示.

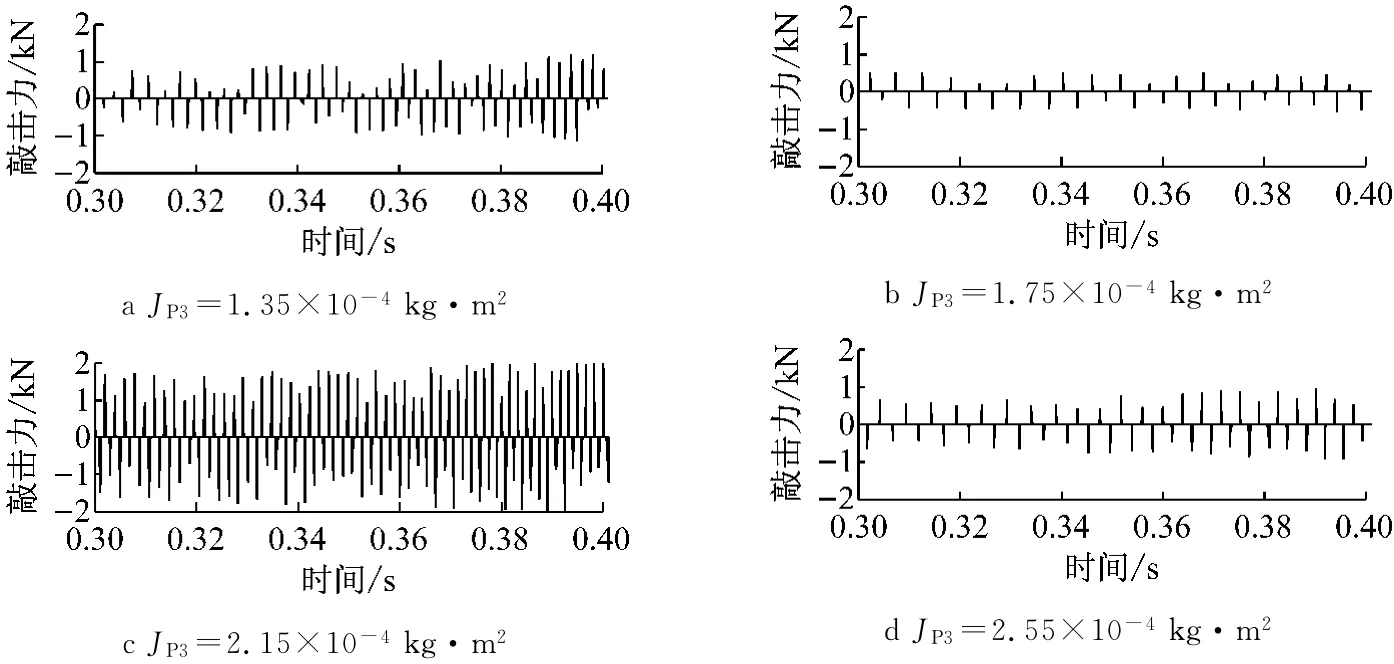
图17 三挡被动齿轮转动惯量影响敲击力图Fig.17 Rattle force of the third gear pair influenced by driven gear torsional inertia

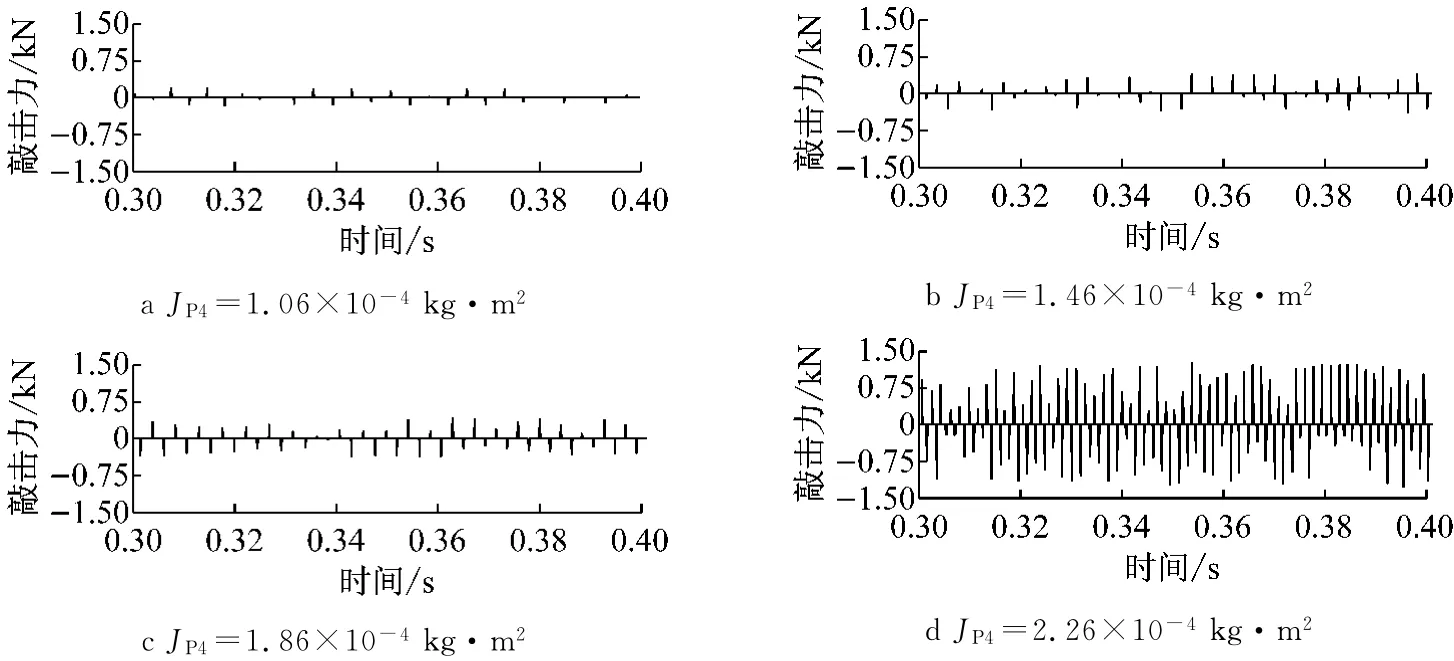
图18 四挡被动齿轮转动惯量影响敲击力图Fig.18 Rattle force of the fourth gear pair influenced by driven gear torsional inertia

图19 五挡被动齿轮转动惯量影响敲击力图Fig.19 Rattle force of the fifth gear pair influenced by driven gear torsional inertia

由图16结果可知，对于二挡齿轮对，被动齿轮转动惯量JG2由6.05×10－4kg·m2变化至7.25× 10－4kg·m2时，敲击频次逐渐增加，然而对于敲击力大小影响规律不明显.由图17结果可知，对于三挡齿轮对，当被动齿轮转动惯量JP3由1.35×10－4kg·m2变化至2.55×10－4kg·m2，敲击频次逐渐增加，对于敲击力大小影响规律不明显.由图18和19结果可知，对于给定的四挡和五挡被动齿轮转动惯量变化范围，随着被动齿轮转动惯量的增加，敲击力和敲击频次均增强.各挡敲击频次随被动齿轮转动惯量增加而增加，是因为当主动齿轮与空套被动齿轮发生敲击后，当空套被动齿轮转动惯量增加时，空套被动齿轮周向转动惯量增加，导致敲击被动齿轮发生敲击弹开，然后很快再次与主动齿轮发生敲击现象，从而使得敲击频次增高.该结果与文献［4］利用台架试验得到的结论保持一致.因此，在变速器主动齿轮设计过程中，应充分考虑各挡位的转动惯量设置（反映在各挡位齿轮具体结构上）.

5 结论

（1）本文利用车辆动力传动系统非线性扭转振动和纵向平移运动耦合模型，再现了车辆处于一挡加速工况时机械变速器各非承载齿轮对的敲击情况.结果表明，随着发动机转速升高，二挡非承载齿轮对敲击力逐渐减小，最后趋于稳定，然而三挡、四挡和五挡非承载齿轮对敲击力逐渐增大，最后趋于稳定.

（2）分析了非承载齿轮对齿侧间隙大小和被动齿轮等效转动惯量大小对敲击强度的影响规律.结果表明，当齿侧间隙位于0.06～0.12mm范围时，随着齿侧间隙增加，各挡位齿轮对敲击力先增加后减小，齿轮对敲击频次单调减小，并且三挡较四挡、五挡轮齿敲击的频次高.对于给定范围内的各挡位被动齿轮转动惯量，随着齿轮等效转动惯量增加，各挡位齿轮对敲击频次单调增加，然而对于敲击力大小，二挡和三挡影响规律不明显，四挡和五挡敲击力单调增加.

［1］Naunheimer H，Bertsche B，Ryborz J，et al.Automotive transmissions：fundamentals，selection，design and application ［M］.Berlin：Springer Science ＆Business Media，2010.

［2］Wang M Y，Manoj R.汽车手动变速箱的齿轮敲击模拟和分析［J］.传动技术，2002，16（4）：27.Wang M Y，Manoj R.Gear rattle modelling and analysis for automotive manual transmissions［J］.Drive System Technique，2002，16（4）：27.

［3］Wang M Y，Zhao W，Manoj R.Numerical modelling and analysis of automotive transmission rattle［J］.Journal of Vibration and Control，2002，8（7）：921.

［4］Robinette D，Beikmann R S，Piorkowski P，et al. Characterizing the onset of manual transmission gear rattle.Part I：experimental results［J］.SAE International Journal of Passenger Cars：Mechanical Systems，2009，2（1）：1352.

［5］Robinette D，Beikmann R S，Piorkowski P，et al.Characterizing the onset of manual transmission gear rattle.Part II：analytical results［J］.SAE International Journal of Passenger Cars：Mechanical Systems，2009，2（1）：1365.

［6］马小英，彭国民，余波.汽车手动变速器怠速敲击噪声研究及优化［J］.汽车工程学报，2011，1（Suppl.1）：44.MA Xiaoying，PENG Guomin，YU Bo.Gear rattle research and analysis for automotive manual transmissions［J］.Chinese Journal of Automotive Engineering，2011，1（Suppl.1）：44.

［7］Yoon J Y，Singh R.Effect of the multi－staged clutch damper characteristics on the transmission gear rattle under two engine conditions［J］.Proceedings of the Institution of Mechanical Engineers，Part D：Journal of Automobile Engineering，2013，227（9）：1273.

［8］Prasad J S，Damodar N C，Naidu T S.Clutch hysteresis maximization for elimination of gear rattle in a passenger bus ［R］.Maharashtra：SAE Technical Paper，2013.

［9］栾文博，吴光强.基于六自由度传动系模型的自动变速器起步仿真［J］.农业机械学报，2013，44（4）：1.LUAN Wenbo，WU Guangqiang.Launch simulation for AMT based on 6－DOF model of vehicle powertrain［J］.Transactions of the Chinese Society for Agricultural Machinery，2013，44 （4）：1.

［10］Ma X，Zhan Z，Peng G，et al.Rattle simulation analysis of a manual gearbox［C］／／Proceedings of the FISITA 2012 World Automotive Congress.Berlin：Springer Berlin Heidelberg，2013：219－233.

［11］刘泽九.滚动轴承应用手册［M］.北京：机械工业出版社，2006.LIU Zejiu.Rolling bearing application manual［M］.Beijing：China Machine Press，2006.

［12］Changenet C，Oviedo－Marlot X，Velex P.Power loss predictions in geared transmissions using thermal networksapplications to a six－speed manual gearbox［J］.Journal of Mechanical Design，2006，128（3）：618.

［13］Canudas de Wit C，Tsiotras P.Dynamic tire friction models for vehicle traction control［C］／／Proceedings of 38th IEEE Conference of Decision and Control.Phoenix：IEEE，1999，4 （3）：3746－3751.

［14］邓堃，李开军，何乐，等.用于车辆紧急制动仿真的动态轮胎模型［J］.农业机械学报，2007，38（12）：11.DENG Kun，LI Kaijun，HE Le，et al.Dynamic tire model for vehicle emergency braking simulation［J］.Transactions of the Chinese Society for Agricultural Machinery，2007，38（12）：11.

Modelling of Manual Transmission Gear Rattle Phenomenon and Its Impact Factors

WU Huwei1，WU Guangqiang1，2
（1.School of Automotive Studies，Tongji University，Shanghai 201804，China；2.Institute of Industrial Science，the University of Tokyo，Tokyo 153－8505，Japan）

Based on basic parameters of vehicle and rotational parameters of real driveline system components，e.g.torsional inertia，stiffness and damping，the coupling model of nonlinear torsional vibration of vehicle powertrain and longitudinal translation was established.With the coupling model，each unloaded gear pair rattling phenomenon was reproduced when the vehicle in gear one was accelerating.Then，gear rattle sensitivity was analyzed for different impact factors.It is shown that appropriate gear backlash and torsional inertia could inhibit the gear rattle phenomenon of manual transmission.

LuGre tire model；nonlinear torsional vibration；coupling model；gear backlash；equivalent torsional inertia成部分，其噪声包括变速器啸叫噪声、齿轮敲击噪声、换挡噪声、轴承噪声和Clonk噪声，是汽车振动噪声的主要来源［1］.对于变速器齿轮系统来说，根据不同的振动状态，噪声主要分为齿轮敲击噪声和啸叫噪声2类，其中齿轮敲击现象是发生在变速器中常啮合非承载齿轮副.当变速器工作在某挡位时，常啮合非承载齿轮对中存在单个齿轮空套在变速器轴上的情况，由于轮齿间存在齿侧间隙，若非承载齿轮副周向运动位移差幅值超过齿侧间隙大小，则将产生敲击现象.变速器齿轮敲击噪声严重影响乘员乘坐舒适性，直接影响车辆品牌形象，因此变速器敲击现象产生机理研究至关重要.

U463.21

A

0253－374X（2016）01－0136－10

10.11908／j.issn.0253－374x.2016.01.020

2015-01-17

国家自然科学基金（51175379）

吴虎威（1987—），男，博士生，主要研究方向为车辆动力传动系统振动噪声.E－mail：1133054＠tongji.edu.cn

吴光强（1965—），男，教授，博士生导师，工学博士，主要研究方向为车辆现代化设计理论及方法以及车辆动力学及其控制.E－mail：wuguangqiang＠tongji.edu.cn