常微分方程数值解法的Matlab计算与可视比较*
2016-12-24孙美玲
孙美玲
(南通职业大学公共教学部,江苏南通226007)
常微分方程数值解法的Matlab计算与可视比较*
孙美玲
(南通职业大学公共教学部,江苏南通226007)
文章研究常微分方程初值问题的数值解法,通过同一个算例、利用Matlab编程实现了一阶欧拉法、二阶预估-校正法、高阶泰勒法、高阶龙格-库塔法,结合数值列表、图文并茂地展现了误差比较与阶数。
常微分方程数值解;Matlab高效计算;精度与误差;方法的阶数
一、概述
常微分方程是描述与研究各事物、现象、运动的演变规律的重要工具,在众多领域应用广泛。理论学习时,对可分离变量方程、齐次与可化齐次方程、一阶线性微分方程、伯努利方程、全微分方程等,可用不同技巧求出其解析解[1]。
然而并不是所有方程都有解析解,求其数值解同样有重大意义。关于常微分方程数值解法,国内往往放在数值分析课程的最后章节,如文献[2],国外则有一本专著[3]。近年来,有效数值解法的研究继续展开,如文献[4]比较了四种算法的实际效果;文献[5]针对四阶方程,提出的Runge-Kutta-Nystrom法在精度和计算效率上都有很好的保证。
二、问题和数值解法
考虑一阶常微分方程的初值问题

这里f(t,u)是光滑函数。我们知道,若满足李普希茨条件|f(t,u1)-f(t,u2)|≤L|u1-u2|,其中L>0,则初值问题(1)存在惟一的连续可微解。
问题(1)的数值解法,即寻找精确解u(t)在一系列等距离散节点t0,t1,…,tn(tj+1=tj+h,h为时间等距步长)的近似值u0,u1,…,un,{un}称为数值解。给出各种数值解法:
1.折线法uj+1=uj+hk1,其中k1=f(tj,uj)。
3.高阶泰勒法,需有光滑的各阶导数f',f'',f(3),…,f(n-1),且利用泰勒展式,定义则高阶泰勒法uj+1=uj+hT(n)(tj,uj)。泰勒法要求较好的光滑性,各阶导数既要存在还要易求。
4.高阶龙格-库塔法,如
二阶龙格-库塔法uj+1=uj+hk2,



三、数值算例
例.分别用欧拉法、预估-校正法、三阶、四阶泰勒法、二阶、三阶、四阶龙格-库塔法求初值问题区间为t∈[0,1],取步长h=0.1。(精确解u(t)=t+e-t)
解:将上述公式转变为简便高效的Matlab编程计算,可得表1。
%精确解



表1 各数值解与精确解之比较
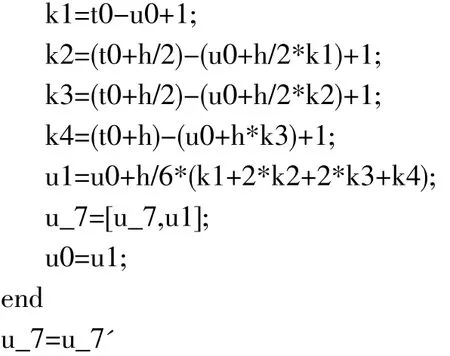

图1 各数值解与精确解
可以验证,欧拉法最简单但精度也最差,其整体截断误差为O(h),为一阶方法;预估-校正法精度有所改进,为二阶方法;高阶泰勒法需简易计算f的高阶导数,对应为O(hn)阶方法,同时也导致更多计算与局限;高阶龙格-库塔法格式对称、应用广泛,对应也为O(hn)阶方法。这促使我们,在复杂多维的常微分方程数值解法中,采用行之有效的高阶数值格式来逼近无精确解的实际模型,也能得到高精度的数值结果。
[1]王高雄,等.常微分方程(第3版)[M].北京:高等教育出版社,2006.
[2]李庆扬,王能超,易大义.数值分析(第5版)[M].北京:清华大学出版社,2008.
[3]J.C.Butcher.Numerical methods for ordinary differential equ ations[M].England:Wiley press,2003.
[4]魏明强.一阶常微分方程数值解中四种算法的实例比较[J].中国传媒大学学报(自然科学版),2016,23(2):41-44.
[5]I.T.Famelis,C.Tsitouras.On modifications of Runge-Kutta-Nystrom methods for solving y(4)=f(x,y)[J].Applied Mathematics and Computation,2016(273):726-734.
We study the initial value problem of ordinary differential equation for efficient numerical solutions. Applying an example and Matlab programing,we fulfill Euler,estimator-corrector,Taylor and Runge-Kutta methods. Through the corresponding tables and figures,we present the error comparison and orders.
numerical solutions of ordinary differential equation;Matlab computation;accuracy and error;order of methods
O17
A
2096-000X(2016)19-0060-02
南通职业大学高等教育教学改革研究课题(编号:2015-QN24);南通职业大学自然科学研究项目(编号:1512105);江苏省高校自然科学研究面上项目(编号:13KJB110030)
孙美玲(1981-),女,江苏南通人,理学博士,讲师,主要研究微分方程理论及其应用。
