基于局部熵的边界与区域水平集图像分割模型

张梦梦, 张泾周, 周三平, 张永涛

(1. 西北工业大学自动化学院, 陕西 西安 710072;2. 西安交通大学人工智能与机器人研究所, 陕西 西安 710049)



基于局部熵的边界与区域水平集图像分割模型

张梦梦1, 张泾周1, 周三平2, 张永涛1

(1. 西北工业大学自动化学院, 陕西 西安 710072;2. 西安交通大学人工智能与机器人研究所, 陕西 西安 710049)

基于图像局部熵提出了一种改进的结合边界信息和区域信息的水平集图像分割模型。利用局部熵构造自适应权重系数,使其能够根据图像性质自适应的决定演化方向,准确引导演化曲线向目标方向移动;然后,根据自适应权重系数定义新的边界指示函数,提高了模型检测弱边界能力,加快了曲线的演化速度;引入Chan-Vese (C-V)模型作为外部能量项,提高了模型的抗噪性,增强了模型分割灰度不均匀图像的能力。通过图像分割实验,验证模型对初始轮廓以及噪声的鲁棒性、分割灰度不均匀图像的能力,并采用客观数值指标,将所提模型与另外三种模型在分割效率和分割准确性方面进行比较。结果表明,提出的模型增强了对噪声的鲁棒性,提高了分割弱边界图像的能力,而且分割灰度不均匀的图像时也取得了比较满意的效果。

图像分割; 水平集方法; 局部熵; 边界信息; 区域信息

0 引 言

图像分割是一个根据区域内相似性以及区域间的相异性而把图像分割成若干区域的过程[1]。图像分割技术是图像处理、图像分析、图像理解、图像识别和计算机视觉领域一项基本而又关键的技术[2-3]。水平集方法的演化实质就是偏微分方程的求解,由图像信息定义能量泛函,根据梯度下降流方法得到一类演化方程,然后对该方程进行求解。对于拓扑变化复杂的图像有较强的适应性并有稳定的数值解。根据约束条件的不同,我们将水平集分割方法划分为两大类:基于边界信息[4-6]和基于区域信息[7-14]的分割模型。

基于边界信息的模型是根据图梯度信息来约束演化曲线,将梯度变化大的区域看作图像边界。这类模型对于边界明确的图像有很好的分割效果,但对于弱边界图像分割效果不理想。例如,测地活动轮廓(geodesic active contour, GAC)模型[4]以及文献[5]提出的无需重新初始化的活动轮廓模型。在文献[5]模型的基础上,文献[6]利用图像梯度信息建立了自适应权重系数模型。由于图像梯度受噪声的影响较大,基于边界信息的模型对噪声有很强的敏感性。基于区域信息的模型利用图像灰度的统计信息来检测目标边界,这类模型不但对噪声具有很强的鲁棒性,而且可以分割弱边界的目标。例如,文献[7]根据图像的全局灰度信息提出了著名的C-V模型,分割弱边界和强噪声图像时取得了很好的效果。为了分割灰度不均匀图像,文献[5]利用图像局部灰度信息建立了局部二值拟合(local binary fitting, LBF)模型[8],该模型对于分割灰度不均匀的图像取得了极大的成功。然而,局部灰度信息的引入,不但使得模型对轮廓初始化比较敏感,而且极易导致演化曲线陷入局部最优解。

本文提出了一种基于边界信息与区域信息的水平集图像分割模型。首先利用图像信息熵建立了权重系数模型与边界指示函数模型,使得模型能够自适应地引导曲线演化方向,并且准确地停止在目标边界上。其次,引入C-V模型作为外部能量项,增强了模型对弱边界图像的处理能力。最后,实验结果表明本文模型不但对噪声具有很强的鲁棒性,而且分割弱边界与灰度不均匀的图像都能取得了令人满意的效果。

1 相关背景

1.1 自适应距离保持水平集演化模型

在文献[5]提出的模型中,v是一个常数,缺乏方向和大小的自适应性。为解决这个问题, 文献[6]提出了一种自适应的演化模型,该模型的能量泛函可以表示为

(1)

(2)

式中,g为边界指示函数；H(z),δ(z)分别为Heaviside函数和Dirac函数;λ和u分别为长度项和距离惩罚项的系数。长度项和面积项能约束演化曲线向目标边界运动,距离惩罚项能够自动补偿水平集函数与符号距离函数之间的偏差,避免了迭代过程中的重新初始化。v(I)为自适应权重系数,Iσ表示经标准差为σ的高斯滤波器平滑后的图像,由图像二阶导数的符号决定演化方向。

虽然该模型能够自适应的调整演化方向,但是,自适应参数的大小仅依赖于图像梯度,这仍然存在一些缺点:

(1) 非边界噪声点处图像梯度也很大,甚至超过边界处梯度的大小,因此仅依据梯度信息判断图像边界,不能处理噪声图像；

(2) 对灰度不均匀,以及弱边界图像处理效果不好。

1.2 C-V模型

Chan和Vese在Mumford-Shah (M-S)模型的基础上提出了C-V模型,能量泛函定义如下:

λ1∫Ω(I(x,y)-c1)2H(φ)dxdy+

λ2∫Ω(I(x,y)-c2)2(1-H(φ))dxdy

(3)

式中,H(z)，δ(z)分别为Heaviside函数和Dirac函数;u为长度项系数;v为面积项系数;λ1,λ2为权重系数,通常取λ1=λ2=1;c1,c2分别为演化曲线内外的灰度均值。当且仅当演化曲线到达目标边界时,能量泛函有最小值。C-V模型对噪声具有鲁棒性,但不能分割灰度不均匀的图像。

1.3 局部熵的定义

信息熵是图像信息论中用来度量信息量的一个概念,Pun提出图像熵的定义如下:

(4)

式中,对数函数一般取2作为底数,也可以取其他数底。

定理 1 对于图像的一个局部窗口,当且仅当局部窗口内的所有灰度值均相等(不为0)时,窗口的熵值最大。

由以上定理可知,在图像的平坦区域局部熵值较大,图像的边界区域局部熵值较小。

2 本文模型

本文提出的模型将边界信息与区域信息结合起来,能量泛函为

E(φ)=wELi+(1-w)ECV(φ)+ER(φ)

(5)

式中,第一项为边界能量项;第二项为CV外部能量项;第三项为正则项。正则项又包括长度约束项以及距离惩罚项。

2.1 自适应权重系数

本文定义的自适应权重系数为

(6)

式中,Iσ表示经标准差为σ的高斯滤波器平滑后的图像;m>0为局部熵的权系数,当图像边界弱,噪声比较大时,可适当的提高m的值,一般取值在(6～15)之间。E为图像的局部熵,增强了边界处响应。

v(I)的选择主要基于以下两方面的考虑。

(1)v(I)的方向:图像的二阶导数在目标边界处异号,演化曲线在目标边界外部时,v>0,曲线向内朝目标边界运动;演化曲线在目标边界内部时v<0,与之前方向相反,曲线向外朝目标方向运动,达到自适应的效果。

(2)v(I)的大小是由图像局部熵和梯度共同决定的。在图像平坦区域,局部熵大,梯度值小,v的值较小,加快曲线演化速度;在目标边界处,局部熵小,梯度值大,v的值较大,增强了零水平集检测弱边界及多层轮廓的能力;在图像噪声点处,局部熵大,梯度值大,v的值较小,曲线继续演化,极大地提高了模型的抗噪性。

2.2 边界指示函数

根据图像局部熵信息,定义如下的边界指示函数:

(7)

式中,m为局部熵的权系数;β(v)是v的函数,可以定义为

(8)

将v中大于其平均值的数记作1,表示边界;将v中小于平均值的数记作0,各向同性区域。在各向同性区域,边界指示函数取值大于0,继续演化;在目标边界区域,边界指示函数取值为0,停止演化。

2.3 水平集方法

将自适应权重系数模型(6)和边界指示函数模型(7)带入到能量函数(5)中,本文提出的模型总的能量泛函为

E(φ)=wELi+(1-w)ECV(φ)+ER(φ)=

(1-w)[λ1∫Ω(I(x,y)-c1)2H(φ)dxdy+

λ2∫Ω(I(x,y)-c2)2(1-H(φ))dxdy]+

(9)

式中,w=0.5 为边界能量项与区域能量项之间的权系数。根据梯度下降流方法,能量函数(9)对应的演化方程可以表示为

(φ)+(1-w)

[δ(φ)(-λ1(I-c1)2+λ2(I-c2)2)]+

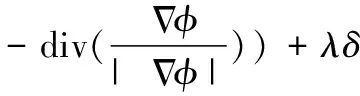
(10)

灰度均值c1,c2可以表示为

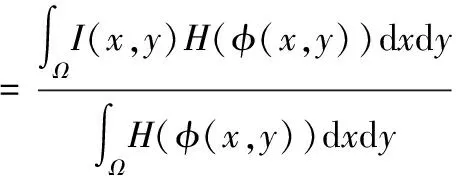
(11)

3 实验结果与分析

通过自然图像与人工合成图像的分割实验,验证模型对初始轮廓以及噪声的鲁棒性、分割灰度不均匀图像的能力、分割的效率和分割的准确性。本文实验环境为Matlab2014Ra、Lenovo PC、Pentium IV处理器,主频3.2 GHz,内存2 GB。实验参数规定为:时间步长Δt=5,惩罚项系数u=0.04,长度项系数λ=0.2,权重w=0.5,λ1=λ2=1,高斯核函数的窗口大小为3×3,标准差σ=2.0,局部熵窗口大小为9×9。

最终算法的实现可按如下步骤进行:

步骤 1 输入待分割图像,初始化演化曲线φ0；

步骤 2 如果|length(ci+1)-length(ci)|>η；

步骤 3 按照方程(11)计算c1(φn),c2(φn)；

步骤 4 分别按照式(6)和式(7)计算自适权系数v(I)以及边界指示函数g；

步骤 5 由方程(10)更新水平集函数；

步骤 6 end；

步骤 7 输出最终的演化结果。

实验 1 验证模型对初始轮廓的鲁棒性

局部熵权系数m=6,初始轮廓的位置分别如图1(a)～图1(c)所示,图1(d)～图1(f)分别为经过2次迭代得到的相应分割结果。可以看出,在初始轮廓的位置、大小都不相同的情况下,本文模型都能够得到正确的分割结果。

图1 模型对初始轮廓的鲁棒性Fig.1 Robustness of our method to different initializations

实验 2 验证模型对噪声的鲁棒性

(1) 对不同噪声的鲁棒性

对未经污染的图像分别加入不同强度的高斯噪声和椒盐噪声,验证模型对各种噪声的抑制能力,实验结果如图2所示。其中,图2(a)为未受污染的原始图像的分割结果,图2(b)和图2(c)分别为图像添加方差0.01和0.1的高斯噪声后的分割结果,图2(c)和图2(d)分别为图像添加方差为0.005和0.01的椒盐噪声后的分割结果。由实验结果可以看出,本文模型对不同强度的高斯噪声以及椒盐噪声都有较好的鲁棒性。

图2 对不同噪声的鲁棒性Fig.2 Robustness to different noisies

(2) 3种模型对噪声鲁棒性的比较

图3中m=6,(a1)，(a2)，(a3)为初始轮廓在图像中的位置；(b1),(b2),(b3)分别为本文模型迭代15次,3次,10次的结果;(c1),(c2),(c3)为C-V模型迭代100次,120次,65次的结果;(d1),(d2),(d3)为文献[6]提出的模型迭代100次的结果。由图3以及表1可以看出,本文模型对噪声具有极好的鲁棒性,而且效率很高,在很少的迭代次数内就能得到准确的分割效果。C-V模型具有一定的抗噪性,但效率不高,对于某些噪声点并不能准确判断出来。而文献[6]提出的模型,则对噪声有很大的敏感性。因此,可以认为本文模型在分割效率和噪声的鲁棒性方面优于另两种模型。这是因为,本文模型采用边缘与区域相结合的方式,根据图像边缘信息可以快速的锁定图像边缘,而区域信息又增加了模型的抗噪性。

图3 3种模型对噪声鲁棒性比较Fig.3 Robustness to noisy comparisons between our model and two other models

图像名称本文模型CPU时间/s迭代次数C⁃V模型CPU时间/s迭代次数文献[6]模型CPU时间/s迭代次数图3(a1)0．2340152．63641003．8688100图3(a2)0．390032．77681206．3336100图3(a3)0．5460102．8236656．9888100

实验 3 灰度不均匀图像的分割

图4为3种模型对灰度不均匀图像项的分割比较,此时m=10,图4(b)～图4(d)分别为3种不同模型的分割结果。对分割结果进行视觉对比可以看到,本文模型对灰度不均匀图像的分割能力较强。

为了从数值对本文提出的模型进行客观的评价,选择4种图像分割准确性评价指标进行验证，分别为真正类(true positive, TP)、假正类(false positive, FP)、精确度(precision, P)、相似度(jaccard similarity, JS)。

图4 3种模型对灰度不均匀图像分割的比较Fig.4 Intensity inhomogeneity image segmentation comparisons between our model and two other models

其中,SG与ST分别为分割的目标区域与实际的目标区域的集合。实际目标区域来源于标准库中的分割结果。

由以上可知一个好的图像分割算法应该取得较高的TP、P、JS值以及较低的FP值。由表2的数据结果可以看出,本章模型的分割准确性要高于其他两种模型。原因在于,首先,本章模型中引入局部熵,在分割过程中考虑了图像的局部信息。其次,定义了新的自适应权重系数,可以更加准确的定位边缘信息。

表2 3种模型分割准确性比较

4 结 论

本文提出了一种基于局部熵的自适应分割模型,引入了C-V模型的外部能量项,使边界信息与区域信息结合起来,同时又可以将局部信息与全局信息结合起来。该模型可以分割噪声图像,对灰度不均匀图像也有很好的分割效果。基于局部熵的自适应权重系数,能够根据图像信息自动的调节演化方向,即使是在噪声的干扰下,也能够准确定位目标边界,极大的提高了模型分割弱边界以及细小目标的能力。此外,通过实验对模型的性能进行了验证,人工合成图像和自然图像的分割实验结果表明本文提出的模型与文献[6]提出的模型,以及基于局部灰度信息的活动轮廓模型相比,除增强了对初始轮廓以及噪声的鲁棒性外,还具有较高的分割效率,对灰度不均匀图像也有较好的分割效果。

[1] Pong F, Chen Z. A new level set method for inhomogenous image segmentation[J].ImageandVisionComputing,2013,(31):809-822.

[2] Zhang Y J. A survey on evaluation method for image segmentation[J].PatternRecognition, 1996, 29(8):1335-1346.

[3] Liu J W. Research of level set method for image segmentation and its applicationsin medical image[D].Hefei:University of Science and Technology of China,2009.(刘军伟. 基于水平集的图像分割方法研究及其在医学图像中的应用[D].合肥:中国科学技术大学,2009.)

[4] Kichenassamy S, Kumar A. Gradient flows and geomerric active contour models[C]∥Proc.oftheIEEEInternationalConferenceonComputerVision, 1995: 810-815.

[5] Li C M, Xu C Y, Gui C F, et al. Level set evolution without re-initialization: a new variational formulation[C]∥Proc.oftheIEEEComputerSocietyConferenceonComputerVisionandPatternRecognition, 2005: 430-436.

[6] He C J, Li M, Zhang Y,Adaptive distance preserving level set evolution for image segmentation[J].JournalofSoftware, 2008, 12:3161-3169.(何传江,李梦,詹毅. 用于图像分割的自适应距离保持水平集演化[J]. 软件学报, 2008, 12:3161-3169.)

[7] Chan T F, Vese L A. Active contours without edges[J].IEEETrans.onImageProcessing, 2001, 10(2): 266-277.

[8] Li C M, Kao C Y. Minimization of region-scalable fitting energy for image segmentation[J].IEEETrans.onImageProcessing, 2008, 17(10): 1940-1949.

[9] Zhang K, Song H, Zhang L. Active contours driven by local image fitting energy[J].PatternRecognition, 2010, 43(4): 1199-1206.

[10] Li C M, Kao C Y. Minimization of region-scalable fitting energy for image segmentation[J].IEEETrans.onImageProces-sing, 2008, 17(10): 1940-1949.

[11] Zhang K, Zhang L, Song H, et al. Active contours with selective local or global segmentation: a new formulation and level set method [J].ImageandVisionComputing, 2010, 28(4): 668-676.

[12] Wang X F, Huang D S, Xu H. An efficient local Chan-Vese model for image segmentation[J].PatternRecognition, 2010, 43(3): 603-618.

[13] Zhou S, Wang J, Zhang S, et al. Active contour model based on local and global intensity information for medical image segmentation[J].Neurocomputing, 2016,186:107-118

[14] Wang L, Li C. Active contours driven by local and global intensity fitting energy with application to brain MR image segmentation[J].ComputerizedMedicalImagingandGraphics, 2009: 520-531.

Boundary and region level set method based on local entropy for image segmentation

ZHANG Meng-meng1, ZHANG Jing-zhou1, ZHOU San-ping2, ZHANG Yong-tao1

(1.SchoolofAutomation,NorthwesternPolytechnicalUniversity,Xi’an710072,China; 2.InstituteofArtificialIntelligenceandRobotics,Xi’anJiaotongUniversity,Xi’an710049,China)

An improved level set method for image segmentation based on image local entropy information is proposed, which combines the edge-based model and the region-based model into a joint framework. Using image local entropy information, an adaptive weighting function is built firstly, which enables the evolving curve choose the evolution direction and move to the object boundary, adaptively. A novel edge indicator function is proposed based on the weighting function, which improves the ability of detecting weak boundary and accelerates the speed of contour evolution. Finally, the Chan-Vese (C-V) model is introduced into the joint framework as an external energy, which enhances the model dealing images with intensity inhomogeneity. In the experiments, the robustness of the method is evaluated to initial contours and noises, and the ability of segmenting images with intensity inhomogeneity. The results show that the proposed method can not only enhance the robustness to noises and improve the ability of segmenting images with weak boundary, but also achieve the satisfying results in segmenting images with intensity inhomogeneity, as compared with the other three methods using objective numerical indicators.

image segmentation; intensity inhomogeneity; local entropy, level set method; active contour model

2016-05-24;

2016-08-03;网络优先出版日期:2016-09-30。

TN 957.52

A

10.3969/j.issn.1001-506X.2016.12.30

张梦梦(1992-),女,硕士研究生,主要研究方向为图形图像处理、图像分割。

E-mail:z_mm@mail.nwpu.edu.cn

张泾周(1960-),男,教授,硕士研究生导师,主要研究方向为生物医学成像。

E-mail:bme@nwpu.edu.cn

周三平(1988-),男,博士研究生,主要研究方向为图像分割、目标检测、多目标跟踪。

E-mail:sanpingzhou@stu.xjtu.edu.cn

张永涛(1992-),男,硕士研究生,主要研究方向为图像处理。

E-mail:252361378@qq.com

网络优先出版地址:http:∥www.cnki.net/kcms/detail/11.2422.TN.20160930.1313.030.html