基于未知输入滤波器的过驱动系统故障诊断方法
2016-12-24王振华
周 萌, 王振华, 沈 毅, 王 艳
(哈尔滨工业大学航天学院, 黑龙江 哈尔滨 150001)
基于未知输入滤波器的过驱动系统故障诊断方法
周 萌, 王振华, 沈 毅, 王 艳
(哈尔滨工业大学航天学院, 黑龙江 哈尔滨 150001)
过驱动系统由于执行器间的冗余性导致故障往往具有严重的耦合性,从而给故障的分离带来很大困难。针对过驱动系统的执行器乘性故障,提出了一种基于未知输入滤波器的故障诊断方法。首先,提出了一种新的未知输入滤波器结构,设计方便。然后,将指定执行器的故障看作未知输入,通过一组结构化残差来实现故障分离,并在此基础上,提出了一种故障估计方法。最后,通过ADMIRE飞行器的近似线性化模型仿真验证了所提方法的有效性。
未知输入滤波器; 故障诊断; 执行器乘性故障; 过驱动系统
0 引 言
为了提高控制系统的可靠性与安全性,故障检测与诊断(fault detection and diagnosis, FDD)技术受到了国际自动控制界的高度重视。自20世纪70年代以来,国内外研究学者在该领域展开了广泛的研究,取得了丰硕的研究成果[1],其中以基于模型的方法研究得最为深入,出现了故障检测滤波器[2]、自适应观测器[3]、未知输入观测器[4]、滑模观测器[5]等诸多方法。
近年来,控制系统的规模越来越大,复杂程度也日益提高,利用单一驱动实现单一控制目标的传统方式已经很难满足要求,因此,具有冗余机构的过驱动系统引起了国内外研究学者的高度重视。过驱动系统是一类控制输入数多于输出数的系统,这些冗余控制不仅为控制器的设计提供更大的自由度,而且由于冗余机构的存在大大提高了系统的容错控制能力,已经在航空航天飞行器[6-7]、水下航行器[8]、四驱汽车[9]等领域得到了广泛的应用。但同时过驱动系统由于执行机构存在严重的功能耦合,故障特征之间也会存在严重的耦合,使得传统的故障诊断方法往往不能有效对其进行故障检测与隔离[10]。
目前过驱动系统的故障检测与诊断还未引起足够的重视,研究方法有限。文献[11]将基于几何方法的故障诊断拓展到过驱动系统,并在F-18HARV飞行器上进行了仿真验证。针对四轮独立驱动电气车辆,文献[12]利用主动故障诊断策略对故障进行估计。文献[13]从故障稀疏性出发,研究了基于稀疏优化算法的卫星四飞轮的故障诊断方法,但该文献仅考虑了加性故障的情况。针对卫星姿态控制系统,文献[10]基于未知输入观测器研究了过驱动系统的故障诊断问题,但设计较为复杂。文献[14]同样利用了未知输入观测器对过驱动系统实现了故障分离,但并没有进一步研究执行器的故障估计问题,给容错控制带来一定的局限性。
未知输入观测器利用自身富裕的自由度可以实现与未建模动态、参数变化、外界干扰等未知输入的解耦,从而消除其对控制系统的影响,已经受到了广泛的研究[15-16]。在实际应用中,系统往往受到随机噪声的影响,对具有未知输入离散随机系统的研究逐渐引起了学者的重视。1969年Friedland提出一种未知输入的二级卡尔曼滤波器,将状态和未知输入进行解耦来进行估计[17]。1987年Kitanidis在未知输入滤波器的基础上研究了具有未知扰动的线性随机系统的无偏最小方差估计,称为未知输入卡尔曼滤波器(unknown input Kalman filter, UIKF)[18]。1997年Darouach等人给出了这种形式下的未知输入卡尔曼滤波器稳定性与收敛性的充要条件[19]。2000年Hsieh将二阶滤波器与Kitanidis未知输入滤波器建立联系,并利用二阶卡尔曼滤波器阶数对状态和未知输入进行估计[20]。文献[21]在文献[18-19]的基础上设计了一个递归滤波器,可以同时估计系统的状态和输入,并且二者之间是相互联系的。文献[23]在文献[22]的基础上针对离散线性时变系统提出了一种传感器故障估计滤波器,该滤波器在形式上与传统滤波器有所不同,更易于实现。
本文在此基础上研究基于未知输入卡尔曼滤波器的过驱动系统的故障诊断。利用未知输入滤波器与未知输入解耦的特性,将执行器故障视为未知输入,然后设计一组结构化残差来实现故障分离。又由于与指定故障解耦的未知输入滤波器的估计值不含有故障信息,因此可以用此估计值来还原真实的故障信息。最后通过ADMIRE飞行器的近似线性化模型进行仿真,验证了本文所提方法能对过驱动系统的单个执行器故障及并发故障实现故障检测、分离与估计。
1 问题描述
考虑带有执行器乘性故障的离散系统:
(1)
式中,x(k)∈Rn,u(k)∈Rm,y(k)∈Rp分别为系统的状态向量,控制输入向量和测量输出向量;A∈Rn×n,Bf∈Rn×m,C∈Rp×n为相应的系统矩阵;ω(k)∈Rn,v(k)∈Rp为不相关的均值为零的高斯随机向量,协方差分别为Q(k)=E[ω(k)·ωT(k)]≥0,R(k)=E[v(k)vT(k)]>0,对于过驱动系统,控制输入的个数多于输出的个数,即满足p Bf=BΛ=B 式中,λi为第i个执行器的失效因子,满足0≤λi≤1(i=1,2,…,m)。当λi=1时,表明第i个执行器没有发生故障;当λi=0时表明第i个执行器发生完全失效故障;当0<λi<1时表明第i个执行器发生部分失效故障。 为了对执行器乘性故障进行诊断,本文首先将乘性故障转化为未知输入进行处理。假设第i个执行器发生故障时,故障是通过输入矩阵B的第i列Bi对系统造成影响,因此式(1)可以写成 (2) 其中 F=Bi (3) fi(k)=(λi-1)ui(k) (4) 式中,下标i表明第i个执行器发生了故障。 不失一般性,本文满足如下假设: 假设 1 系统状态向量x(k)与噪声ω(k),v(k) 不相关,满足 (5) 假设 2 矩阵C,F满足 rank(CF)=rank(F) (6) 本文主要设计一组未知输入滤波器对过驱动系统执行器的乘性故障进行故障检测、分离与估计。首先,假设过驱动系统仅有一个执行器发生故障,针对过驱动系统的m个执行器,设计m个未知输入滤波器,使得只有第i个未知输入滤波器的残差不受第i个执行器故障的影响,并以此为基础实现故障的分离与估计。然后,将该故障分离与估计的方法推广到有并发故障的情况。接下来,在第2节和第3节中分别具体介绍未知输入滤波器的设计方法和故障诊断策略。 本节只针对第i个执行器发生故障的情况下设计一个未知输入滤波器,第3节中的故障诊断策略将主要根据本节设计的未知输入滤波器选出正确的故障情形。 借鉴文献[22-23]的思想,针对系统式(2)设计未知输入滤波器形式为 (7) 令 T+NC=In (8) 式中,In为单位矩阵,对式(2)左边乘以T+NC得 x(k+1)=(T+NC)x(k+1)=Tx(k+1)+ NCx(k+1)=TAx(k)+TBu(k)+TFfi(k)+ Tω(k)+NCx(k+1) (9) 设未知输入滤波器的状态估计误差向量为 (10) 则式(9)-式(7)可得 e(k+1)=(TA-L(k)C)e(k)+TFfi(k)+ Tω(k)-L(k)v(k)-Nv(k+1) (11) 为了使未知输入滤波器对指定的故障f(k)不敏感,设计矩阵T,使其满足 TF=0 (12) 则 e(k+1)=(TA-L(k)C)e(k)+ Tω(k)-L(k)v(k)-Nv(k+1) (13) 为了得到未知输入下的状态估计最优值,设计增益矩阵使得估计误差的协方差最小。定义估计误差的协方差为 P(k)=E[e(k)e(k)T] (14) 将式(13)代入式(14)得 P(k+1)=E[e(k+1)eT(k+1)]=(TA-L(k)C)P(k)(TA-L(k)C)T+TQTT+L(k)RLT(k)+NRNT= TAP(k)(TA)T-TAP(k)(L(k)C)T-L(k)CP(k)(TA)T+L(k)CP(k)(LC)T+TQTT+L(k)RLT(k)+NRNT= TAP(k)(TA)T-TAP(k)(L(k)C)T-L(k)CP(k)(TA)T+TQTT+NRNT+L(k)(CPT(k)C+R)LT(k) (15) 因为R为正定矩阵,则CP(k)CT+R为正定矩阵,令 G(k)GT(k)=CP(k)CT+R (16) H(k)=TAP(k)CTG-1(k) (17) 代入整理得 P(k+1)=TAP(k)(TA)T+TQTT+NRNT+L(k)G(k)GT(k)LT(k)-H(k)GT(k)LT(k)-L(k)GT(k)HT(k)= TAP(k)(TA)T+TQTT+NRNT+L(k)G(k)GT(k)LT(k)-H(k)GT(k)LT(k)-L(k)GT(k)HT(k)+H(k)HT(k)- H(k)HT(k)=TAP(k)(TA)T+TQTT+NRNT+(L(k)G(k)-H(k))(L(k)G(k)-H(k))T-H(k)HT(k) (18) 为了使P(k+1)最小,令 L(k)G(k)=H(k) (19) 对式(19)左右两边乘以GT(k)得 L(k)G(k)GT(k)=H(k)GT(k) (20) 即 L(k)(CP(k)CT+R)=TAP(k)CT (21) 求解得未知输入滤波器的增益矩阵为 L(k)=TAP(k)CT(CP(k)CT+R)-1 (22) 将式(22)代入式(18)可得 P(k+1)=TAP(k)(TA)T+TQTT+NRNT- (TAP(k)CTG-1(k))(TAP(k)CTG-1(k))T= TAP(k)(TA)T+TQTT+NRNT- TAP(k)CT(CP(k)CT+R)-1CP(k)(TA)T (23) 由式(8)和式(12)可得 (In-NC)F=0 (24) 在满足假设2的情况下可得 N=F(CF)++S(I-(CF)(CF)+) (25) 式中,S为任意选取的矩阵;(CF)+为矩阵CF的伪逆,进一步可以求得矩阵T。至此,未知输入滤波器设计完毕。 基于上述未知输入滤波器算法,本节主要针对过驱动系统,分别给出单一故障及并发故障情况下的故障检测、分离与估计策略。 3.1 单一故障的检测、分离与估计 首先,假设过驱动系统在某一时刻仅有一个执行器发生故障,针对具有m个执行器的过驱动系统式(2),设计m个未知输入卡尔曼滤波器,使其分别于特定的某一个执行器解耦,然后构造一组结构化残差实现执行器的故障分离。当成功对故障进行分离后,提出了一种利用不含故障的状态估计值的故障估计方法。该方法的原理图如图1所示。 图1 只考虑单一故障时的故障诊断原理示意图Fig.1 Fault diagnosis scheme for single fault scenario 设计m个未知输入卡尔曼滤波器形式为 (26) 式中,下标i代表与第i个执行器解耦的未知输入滤波器,且Ti,Ni满足 TiBi=0 (27) Ti+NiC=In (28) 式中,Bi为B的第i列。 定义残差为 (29) 在ω(k),v(k)为零均值的高斯白噪声条件下,若所有执行器均未发生故障,则各滤波器生成的残差均为零均值的白噪声,而一旦有某个执行器发生故障,则与之相对应的未知输入滤波由于与该故障解耦,则残差中不包含故障信息,而其他滤波器生成的残差中则包含故障信息,因此残差会很大。基于此思路,预先根据经验给定阈值为εi,当所有的残差满足ri(k)≤εi(i=1,2,…,m),则表明所有的执行器均没有发生故障,但是如果有一个残差ri(k)>εi,则表明有执行器发生了故障。当仅有一个残差小于给定阈值而其他残差均超过给定阈值时,说明该系统仅有一个执行器发生了故障。而当所有的残差均超过给定的阈值时,则表明系统至少有两个执行器同时发生了故障。 当过驱动系统仅有一个执行器发生故障时,因为仅有一个残差小于给定阈值,因此可通过在m个残差中选出最小的ri(k)所对应的指标i,即代表第i个执行器发生了故障。 {‖ri‖} (30) 当成功对故障进行分离后,与之对应的第i*个未知输入滤波器的估计结果由于与故障解耦,该状态估计值不受故障的影响,因此可以利用其对故障进行估计。采用文献[24]的思路,利用这一时刻的估计值来近似上一时刻的故障信息,即 y(k+1)=Cx(k+1)+v(k+1)≈ (31) 当只有一个执行器发生故障时,只有第i*个执行器的失效因子不为零,其他全部为零。由式(4)可以求得执行器失效因子矩阵为 (32) 3.2 考虑并发故障的检测、分离与估计 接下来,针对过驱动系统提出了存在并发故障情况下的故障检测、分离与估计算法。 图2 考虑并发故障时故障诊断原理示意图Fig.2 Fault diagnosis scheme for concurrent faults scenario (33) 式中,下标i,j代表同时与第i个执行器和第j个执行器解耦的未知输入滤波器,且Tij,Nij满足 TijBij=0,i,j=1,2,…,m (34) Tij+NijC=In (35) 其中,Bij为输入矩阵B的第i列和第j列组成的矩阵。 定义残差为 (36) (37) 为了验证本文所提方法的有效性,本节利用ADMIRE飞行器的近似线性化模型进行仿真验证[25]。状态向量为x=[αβpqr]T,分别为攻角(°),侧滑角(°),滚转角速率((°) /s),俯仰角速率((°)/s)和偏航角速率((°)/s)。控制为u=[δrcδlcδroeδrieδlieδloeδr],分别为鸭翼的右偏角(°)和左偏角(°),升降副翼的右外偏角(°)和右内偏角(°),升降副翼的左内偏角(°)和左外偏角(°)以及方向舵的偏角(°)。系统矩阵为 C= 首先对系统进行离散化,采样时间设为Δt=0.1 s,通过近似离散化公式可以得到离散化矩阵Ak,Bk为 Ak=eAΔt (38) (39) S= 情况 1 单一故障时 假设过驱动系统仅有一个执行器发生故障,针对该模型的7个执行器,设计7个未知输入滤波器,根据式(27)和式(28)可求取7组相应的Ti和Ni,然后通过式(22)和式(23)迭代求得未知输入滤波器的增益矩阵Li。 假设当0 s≤t<30 s时所有的执行器均没有发生故障,当30 s≤t<60 s时第5个执行器发生部分时变失效故障,当60 s≤t<100 s时第5个执行器恒定失效90%。故障表达式为 Λ= (40) 情况 2 两个执行器同时发生故障时 针对两个执行器同时发生故障的情况,本文设计了21个滤波器,使其分别对任意两个执行器进行解耦。 假设当0 s≤t<40 s时所有的执行器均没有发生故障,当40 s≤t<100 s时第2个执行器和第6个执行器同时发生部分失效故障。故障表达式为 (41) 图3~图5为单一时变故障情况下的未知输入滤波器的残差结果和故障估计结果。由图3可以看到当0 s≤t<30 s所有的残差都小于预先设定的阈值,表明所有的执行器均未发生故障,而当30 s 图3 单一故障时的前7个滤波器的残差Fig.3 Residuals generated by the 7 filters for single fault scenario 图4 单一故障时21个滤波器的残差Fig.4 Residuals generated by the 21 filters for single fault scenario 图5 单一故障时的故障估计结果Fig.5 Fault estimation results for single fault scenario 图6~图8为并发故障时的故障分离与估计结果。由图6可以看出,当两个执行器同时发生故障时,针对单一故障设计的7个滤波器的残差在40 s≤t<100 s内均高于设定阈值,说明该过驱动系统有多个执行器同时发生了故障。由图7可以看出,针对两个执行器解耦的滤波器生成的残差中只有r26小于阈值,其余均高出给定阈值,表明第2个执行器和第6个执行器同时发生了故障。图8为故障估计结果,可以看出本文提出的设计方法准确地估计出第2个执行器和第6个执行器的乘性失效故障。 图6 并发故障时的前7个滤波器的残差Fig.6 Residuals generated by the 7 filters for concurrent fault scenario 图7 并发故障时的21个滤波器的残差Fig.7 Residuals generated by the 21 filters for concurrent fault scenario 图8 并发故障时的故障估计结果Fig.8 Fault estimation results for concurrent fault scenario 本文针对过驱动系统的执行器乘性故障诊断,提出了一种区别于常用结构的未知输入滤波器,其形式更易于设计实现。利用未知输入滤波器与未知输入的解耦特性来实现过驱动系统的执行器乘性故障的故障检测与分离,并在此基础上提出一种故障估计的方法。仿真结果验证了所提方法的正确性与有效性。 [1] Hwang I, Kim S W, Kim Y D, et al. A survey of fault detection, isolation and reconfiguration methods[J].IEEETrans.onControlSystemsTechnology, 2010, 18(3): 636-653. [2] Zhong M Y, Ding S X, Lam J, et al. An LMI approach to design robust fault detection filter for uncertain LTI systems[J].Automactica, 2003, 39(3): 543-550. [3] Meng L Y, Jiang B. Fault diagnosis based on the nonlinear adaptive observer[J].SystemsEngineeringandElectronics, 2008, 30(7): 1317-1319.(孟令雅,姜斌.基于非线性自适应观测器的故障诊断[J].系统工程与电子技术,2008,30(7): 1317-1319. [4] Liu L J, Shen Y, Zhang M. Adaptive robust fault-tolerant H control design based on an adaptive fault observer[C]∥Proc.ofthe31thChineseControlConference, 2012: 5209-5214. [5] Liu C, Li Y H. Design of high gain observers with sliding mode for the actuator robust fault detection of nonlinear system[J].SystemsEngineeringandElectronics, 2014, 36(8):1626-1631.(刘聪,李颖晖.基于高增益滑模观测器的非线性系统执行器鲁棒故障检测[J].系统工程与电子技术,2014,36(8):1626-1631.) [6] Alwi H, Edwards C. Fault tolerant control using sliding modes with online control allocation[J].Automatica, 2008, 44(7): 1859-1866. [7] Chen Y, Dong X M, Xue J P, et al. Constrained adaptive control allocation for multi effector flight control system[J].SystemsEngineeringandElectronics,2011, 33 (5): 1118-1123.(陈勇,董新民,薛建平,等.多操纵面飞控系统约束自适应控制分配策略[J].系统工程与电子技术,2011,33(5):1118-1123.) [8] Johansen T A, Fuglset T P, Tondel P, et al. Optimal constrained control allocation in marine surface vessels with rudders[J].ControlEngineeringPractice,2008, 16(4): 457-464. [9] Mohand A D, Rochdi M, Belkacem O B, et al. Fault diagnosis and fault tolerant control of an electric vehicle overactuated[J].IEEETrans.onVehicularTechnology, 2013, 62(3): 986-994. [10] Cristofaro A, Johansen T A. Fault tolerant control allocation using unknown input observers[J].Automatica, 2014, 50(7): 1891-1897. [11] Meskin N, Khorasani K. Fault detection and isolation of actuator faults in overactuated systems[C]∥Proc.oftheAmericanControlConference, 2007: 2527-2532. [12] Wang R, Wang J. Fault-tolerant control with active fault diagnosis for four-wheel independently driven electric ground vehicles[C]∥Proc.oftheAmericanControlConference, 2011: 3954-3959. [13] Wang Z H, Shen Y, Zhang X, et al. Fault diagnosis for satellite attitude control systems with four flywheels[J].JournalofDynamicSystems,MeasurementandControl,2014, 136: 041016. [14] Fonod R, Henry D, Bornschlegl E, et al. Thruster fault detection, isolation and accommodation for an autonomous spacecraft[C]∥Proc.ofthe19thInternationalFederationofAutomaticControlWorldCongress, 2014: 10543-10548. [15] Liu L J, Shen Y, Dowell E H. Integrated adaptive fault-tolerantH∞output feedback control with adaptive fault identification[J].JournalofGuidance,ControlandDynamics, 2012, 35(3): 881-889. [16] Shen Y, Liu L J, Dowell E H. Adaptive fault-tolerant robust control for a linear system with adaptive fault identification[J].IETControlTheoryandApplications, 2013, 7(2): 246-252. [17] Friedland B. Treatment of bias in recursive filtering[J].IEEETrans.onAutomaticControl, 1969, 14(4):359-367. [18] Kitanidis P K. Unbiased minimum variance linear state estimation[J].Automatica, 1987, 23(6): 775-778. [19] Darouach M, Zasadzinski M. Unbiased minimum variance estimation for systems with unknown exogenous inputs[J].Automatica, 1997, 33(4): 717-719. [20] Heieh C S. Robust two-stage Kalman filters for systems with unknown inputs[J].IEEETrans.onAutomaticControl, 2000, 45(12): 2374-2378. [21] Gillijins S, Moor B D. Unbiased minimum-variance input and state estimation for linear discrete-time systems[J].Automatica, 2007, 43(1): 111-116. [22] Wang Z H, Yi S, Zhang X L, et al. Observer design for discrete-time descriptor systems: an LMI approach[J].SystemsandControlLetters, 2012, 61(6): 683-687. [23] Wang Z H, Mickael R, Didier T, et al. Sensor fault estimation filter design for discrete-time linear time-varying systems[J].ActaAutomaticaSinica, 2014, 40(10): 2364-2369. [24] Jiang B, Chowdhury F N. Fault estimation and accommodation for linear MIMO discrete-time systems[J].IEEETrans.onControl,SystemsTechnology, 2005, 13(3): 493-499. [25] Ye S J, Zhang Y M, Wang X M, et al. Robust fault tolerant control using on-line control re-allocation with application to aircraft[C]∥Proc.oftheAmericanControlConference, 2009: 5534-5539. 王振华(1987-),通信作者,男,讲师,博士,主要研究方向为航天器故障诊断与容错控制、描述系统故障诊断。 E-mail:zhenhua.wang@hit.edu.cn 沈 毅(1965-),男,教授,博士,主要研究方向为控制系统的故障诊断、飞行器制导与控制技术、超声成像技术。 E-mail:shen@hit.edu.cn 王 艳(1959-),女,教授级高工,博士,主要研究方向为自动化检测与控制、信号处理。 E-mail:wyabc@hit.edu.cn Unknown input filter based fault diagnosis method for over-actuated systems ZHOU Meng, WANG Zhen-hua, SHEN Yi, WANG Yan (SchoolofAstronautics,HarbinInstituteofTechnology,Harbin150001,China) For over-actuated systems, due to the redundancy of the actuators, there is often serious coupling between the actuator faults, which may bring great difficulty to fault detection, especially for fault isolation. To overcome the drawbacks, a fault diagnosis method for over-actuated systems is proposed with unknown input filters. Firstly, a new unknown input filter is proposed with a novel structure, which is more convenient to implement. And then, by considering an actuator fault as the unknown input vector, a set of structure residuals is achieved to fault isolate. Next, a fault estimation method is presented based on the isolation result. Finally, the presented method is applied to the ADMIRE aircraft control system, and simulation results illustrate the method is able to detect and estimate the actuator multiplicative fault effectively. unknown input filter; fault diagnosis; actuator multiplicative fault; over-actuated system 2015-08-17; 2016-10-17;网络优先出版日期:2016-10-27。 国家自然科学基金(61273162, 61403104)资助课题 TP 273 A 10.3969/j.issn.1001-506X.2016.12.24 周 萌(1988-),女,博士研究生,主要研究方向为故障诊断与容错控制。 E-mail:zhoumeng6932@126.com 网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20161027.1605.020.html2 未知输入卡尔曼滤波器设计

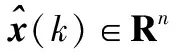

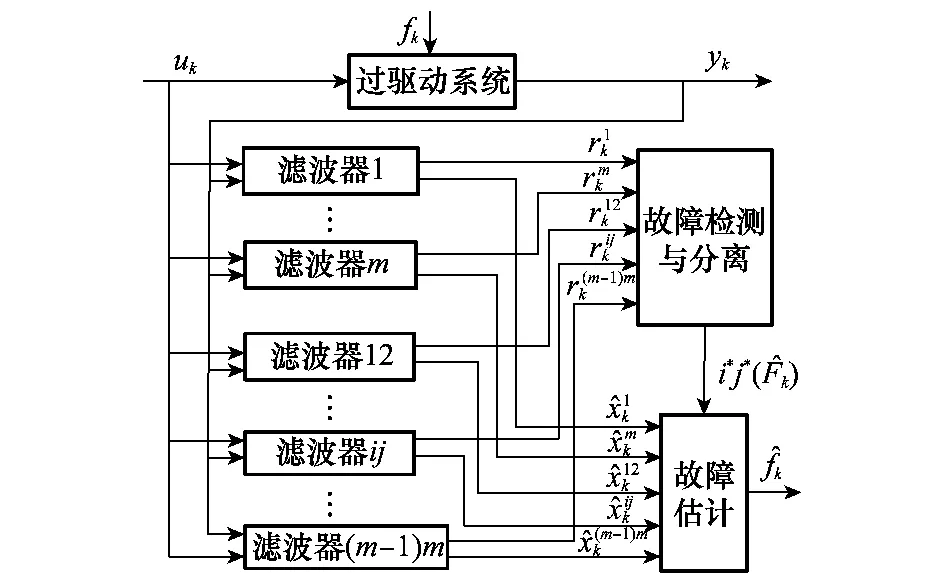
3 故障诊断方法



4 仿真验证




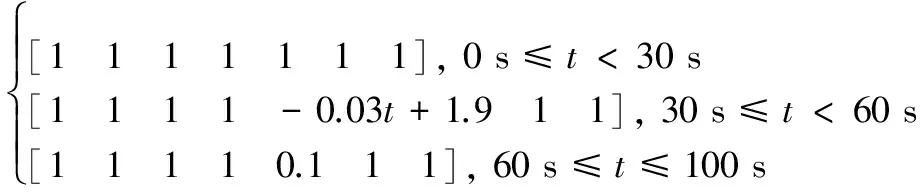







5 结 论
