基于扩展H∞滤波的SINS/AMM机载组合导航技术

2016-12-24申杰亮朱欣华

系统工程与电子技术 2016年12期

关键词：不确定性气动滤波

申杰亮, 王宇, 朱欣华, 苏岩

(南京理工大学机械工程学院, 江苏南京 210094)

基于扩展H∞滤波的SINS/AMM机载组合导航技术

申杰亮, 王宇, 朱欣华, 苏岩

(南京理工大学机械工程学院, 江苏南京 210094)

研究了飞机运动模型(aircraft motion model, AMM)与中、低精度捷联惯导系统(strapdown inertial navigation system, SINS)相融合的组合导航技术。针对由于气动系数的不准确所导致的系统方程的不确定性以及观测方程和噪声的不确定性问题,提出采用基于极小极大准则的扩展H∞滤波(extendedH∞filter, EHF)方法用于组合导航系统的数据融合。以某小型固定翼无人机为研究对象,分别从时域、频域的角度进行仿真实验的验证与分析。实验结果表明,在SINS/AMM组合导航过程中,与扩展卡尔曼滤波(extended Kalman filter, EKF)相比,EHF具有更好的鲁棒性,并且可以提高35%左右的导航精度。

飞机运动模型; 捷联惯导系统; 系统和噪声的不确定性; 扩展H∞滤波

0 引言

捷联惯导系统(strapdown inertial navigation system, SINS)与全球定位系统(global positioning system, GPS)的惯性/卫星组合导航是目前最主要的机载导航系统。SINS输出的导航参数与GPS信号融合后,实时补偿SINS的累积误差,可以实现高精度的导航。但GPS信号在某些情况下不稳定,如GPS在上电的初始阶段,由于无法立即搜索到足够数量的卫星,组合系统无法完成精确的数据融合;在有较大较多障碍物的环境下,GPS会因遮蔽而无法使用;另外,GPS也会受到自然界或人为的电磁干扰等。

飞机运动模型(aircraft motion model, AMM)基于速度、角速度和姿态微分方程,利用已知的飞机油门、舵机等控制输入量和初始运动状态,可实时推算出机体的姿态、速度和位置。在机载导航中,SINS/AMM的组合可以在某种程度上替代SINS/GPS组合导航,且无需增加外部传感器,具有低成本、自主性强的优点。Koifman M最早于1999年提出了利用飞机运动模型辅助低精度惯导系统的方法,利用扩展卡尔曼滤波(extended Kalman filter, EKF)仿真验证其可行性,并分析了飞行机动特性、气动参数的不准确性对导航精度的影响[1];文献[2]将飞机运动模型和惯导系统的组合运用到直升飞机的导航中,通过仿真和飞行实验,验证了该组合方案可以达到较好的导航精度;载体运动模型和惯导系统组合的方法还成功地运用到车载导航[3]、潜艇导航[4-6]以及炮弹制导中[7-9]。以上研究均采用EKF来进行数据融合,但EKF无法解决由于载体运动模型和噪声的不确定性所致导航误差的问题,且EKF自身也包含一定的线性化误差。

本文以某小型固定翼无人机为研究对象,设计了中、低精度SINS与AMM的组合导航方案。针对SINS/AMM组合导航中系统方程、量测方程以及噪声的不确定性问题,设计了鲁棒性更强的扩展H∞滤波(extendedH∞filter, EHF) 算法。仿真实验结果表明,与EKF算法相比较,EHF可以达到更高的导航精度。

1 SINS/AMM组合导航系统的建立

1.1 SINS误差模型

SINS误差模型表示如式(1)所示,地理坐标系n系指向北、东、地。

(1)

式中

1.2 AMM及线性化误差模型

AMM包括动力学模型和运动学模型。飞机动力学模型以速度、角速度微分方程的形式描述了飞机在外力和外力矩作用下的运动规律;而飞机运动学模型则通过姿态、位置微分方程来描述机体绕质心的转动和质心的位移[11]。

以某常规布局的小型螺旋桨式固定翼无人机为例,速度微分方程在b系中投影为

(2)

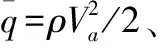
(3)

角速度微分方程在b系中投影为

(4)

(5)

用于姿态计算的姿态角微分方程为

(6)

(7)

基于小扰动原理,在平衡点处对式(7)做泰勒级数展开并仅保留线性项,得到的包含状态量XAMM=[δu,δw,δq,δθ]T的线性纵向运动误差微分方程为

(8)

式中,FAMM为线性化过程中由式(7)计算的Jacobian矩阵,飞机纵向气动系数CX,CZ,Cm的不准确会导致不确定性ΔFAMM的产生;WAMM=[wδu,wδw,wδq]T表示因线性化而产生的不确定性噪声,可近似为白噪声。而高度h和俯仰角θ等纵向参数的保持与控制,由基于飞机纵向通道线性化模型设计的经典PID控制实现,其原理如图1所示。

图1 飞机纵向通道控制原理图Fig.1 Principle for aircraft’s longitudinal control

1.3 SINS/AMM组合导航系统滤波模型

建立如式(9)所示的线性化的系统方程和观测方程:

(9)

系统方程由式(1)、式(8)组成:

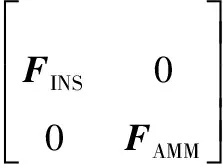
(10)

那么,SINS/AMM组合导航系统设计如图2所示,经过滤波器估计得到的状态量实时闭环补偿到SINS和AMM中。

图2 SINS/AMM组合导航系统原理图Fig.2 Principle for SINS/AMM integrated navigation

2 扩展H∞滤波器的设计

由SINS/AMM组合导航系统建立过程可以看出,系统状态方程、观测方程以及系统噪声和观测噪声均存在一定的不确定性。飞机初始气动系数分析误差以及飞行条件和飞行环境的变化,使得气动系数C存在一定的不准确性和时变性,导致系统状态方程的不确定性ΔF;而观测方程矩阵H由于近似计算会产生不确定性ΔH;系统和观测噪声同样存在统计特性的不确定性,但均可视为能量有界噪声。针对系统和噪声的不确定性,本文采用鲁棒性更强的EHF算法实现信息的融合。

(11)

与最小方差估计理论不同,H∞滤波旨在保证系统由输入噪声至估计误差的传递函数的H∞范数最小,等价于输入信号至输出信号能量最大增益的最小化,使得滤波器具有更强的鲁棒性。其相应的代价函数[12-14]为

(12)

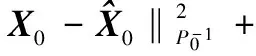
(13)

则EHF的递推过程[14-15]为

(14)

(15)

(16)

(17)

(18)

θ的选取应该满足:

(19)

(20)

3 仿真验证与分析

本文仿真包含3个模块。

(1) AMM的仿真

选取某型号的小型螺旋桨式固定翼无人机,其结构参数、气动参数以及螺旋桨参数标称值可以较精确获得[16],如表1所示。飞机飞行轨迹设定为定高定直线无侧滑匀速飞行。飞行初始状态量、螺旋桨转速、舵机的输入量可经过配平得到,如表2所示。利用飞行的初始状态、结构和气动参数以及AMM可以逐步解算出飞机的各项运动参数。仿真中忽略风速的影响。

表1 飞机参数标称值设定

表2 配平状态设定

(2) 机载SINS的仿真

取中等精度的惯性测量单元,设定陀螺的常值漂移为1(°)/h,随机噪声为0.5(°)/h;加速度计的常值偏置为0.1 mg,随机噪声为0.05 mg。不考虑惯导解算初始误差。

(3) EKF、EHF滤波器的仿真

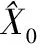
Q=diag{(0.5°/h)2(0.5°/h)2(0.5°/h)2(0.05mg)2(0.05mg)2

(0.05mg)2(1e-4m/s)2(1e-4m/s)2(1e-5rad/s)2}

R=diag{ (0.01m/s)2(0.01m/s)2(0.01m/s)2}

P0=diag{(0.2°)2(0.2°)2(0.2°)2(0.1m/s)2

(0.1m/s)2(0.1m/s)2(2e-5°)2(2e-5°)2(0.1m)2

(0.5°/h)2(0.5°/h)2(0.5°/h)2(0.1mg)2(0.1mg)2

(0.1mg)2(0.1m/s)2(0.1m/s)2(0.001rad/s)2(0.15°)2}

EHF的加权矩阵以及相应的参数设定:

Sk=Pk;QH=5Q;RH=5R,θ=5

仿真过程中,SINS和AMM均以0.01 s为采样周期,滤波器的滤波周期为1 s。其中,AMM的纵向气动参数(包括阻力系数CX、升力系数CZ、俯仰力矩系数Cm)分别使用表1中的标称值以及分别增加0.1%、1%的随机误差的不准确值。

在这3种情况下,分别利用EKF和EHF算法,对比各个导航参数的闭环补偿效果,如图3～图6所示。表3为各纵向导航参数误差均值绝对值的对比。

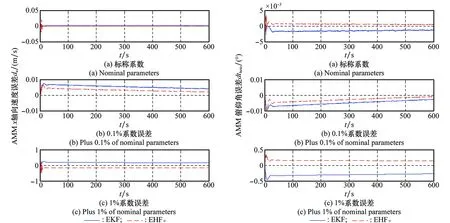
图5 AMM x轴速度误差比较图6 AMM俯仰角误差比较Fig.5 Comparison of AMM velocity error alone x-axisFig.6 Comparison of AMM pitch error

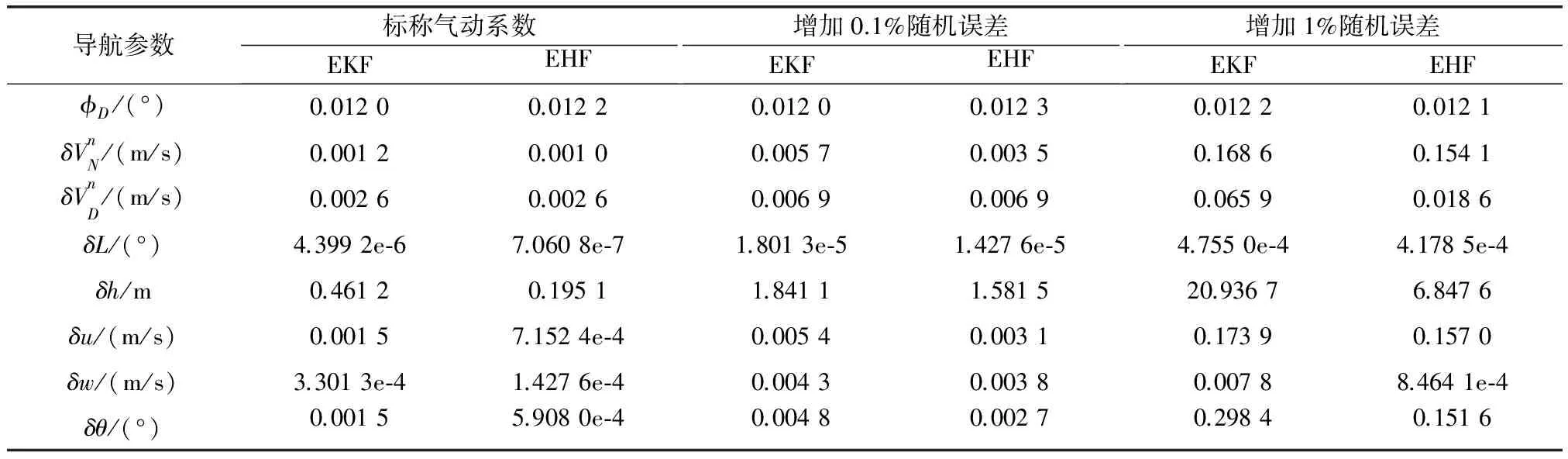
导航参数标称气动系数EKFEHF增加0．1%随机误差EKFEHF增加1%随机误差EKFEHFϕD/(°)0．01200．01220．01200．01230．01220．0121δVnN/(m/s)0．00120．00100．00570．00350．16860．1541δVnD/(m/s)0．00260．00260．00690．00690．06590．0186δL/(°)4．3992e⁃67．0608e⁃71．8013e⁃51．4276e⁃54．7550e⁃44．1785e⁃4δh/m0．46120．19511．84111．581520．93676．8476δu/(m/s)0．00157．1524e⁃40．00540．00310．17390．1570δw/(m/s)3．3013e⁃41．4276e⁃40．00430．00380．00788．4641e⁃4δθ/(°)0．00155．9080e⁃40．00480．00270．29840．1516

由图表分析可得:①随着气动系数误差的增加,导航误差总体增大,主要是因为AMM误差的增大;②采用标称气动系数或者包含随机误差的气动系数,EHF滤波的精度整体高于EKF滤波的精度,主要是由于EHF对于系统方程、量测方程以及噪声的不确定性都具有更高的鲁棒性;③对于采用标称气动系数的组合系统,与EKF相比,EHF滤波后的SINS的位置误差和AMM的速度、位置误差均有60%左右精度的提升;④气动系数分别加入0.1%、1%的随机误差后,除了SINS的俯仰角误差φD外,两种情况下的导航精度分别有25%和45%左右的提高。即气动系数误差越大,越能体现EHF的鲁棒性;⑤相比于EKF,利用EHF算法使得SINS/AMM组合导航精度平均提高了35%左右。

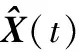
(21)

(22)

在图7、图8中,蓝色实线簇表示采用EKF时的传递函数幅频特性曲线,红色虚线簇则表示采用EHF时的幅频特性。局部放大图可以看出,在EKF或EHF的作用下,随着纵向气动系数随机误差大小的递增,幅频特性曲线上移,即幅值增加。EHF的幅值总体比EKF小约25dB左右,即由输入噪声至状态估计误差的增益小于EKF。此外,EHF滤波器幅频特性曲线的包线相对于EKF更为集中,说明在系统和噪声存在不确定性的情况下,EHF具有更好的鲁棒性。

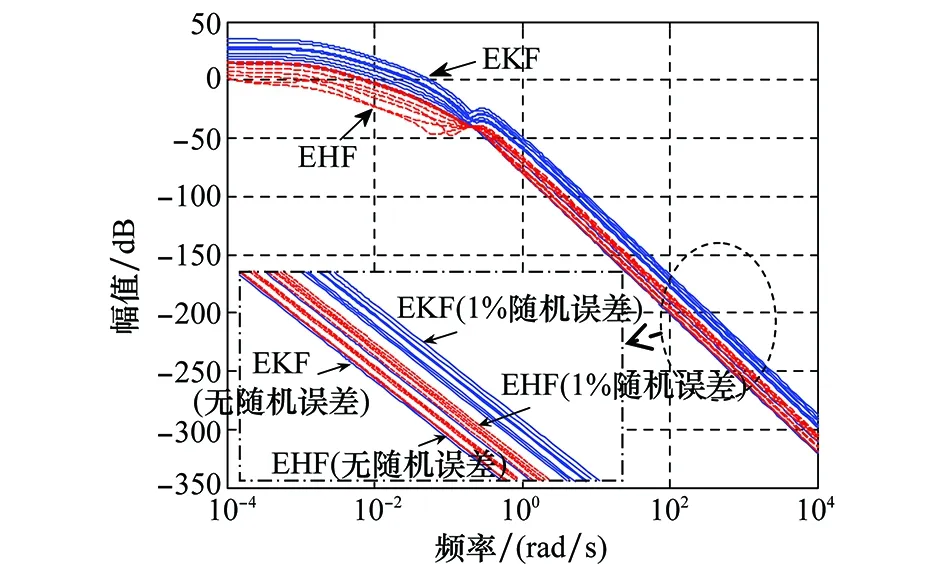
图7 输入至输出δh的幅频特性Fig.

图8 输入至输出δu的幅频特性Fig.

4 结论

本文主要研究了AMM与中、低精度的SINS的组合导航技术。针对SINS/AMM在融合过程中系统方程、观测方程和噪声统计特性的不确定性,提出了基于极小极大准则的EHF组合导航系统信息融合方法,可以在卫星信号不稳定的情况下,实现低成本、自主性强的组合导航。仿真结果表明,与EKF算法相比,EHF具有更好的鲁棒性,并且可提高35%左右的导航精度。在后续的研究中,需要根据不同的飞行环境、飞行机动条件,针对飞机气动系数的不确定性问题,开展相应的补偿技术研究,从而进一步提高SINS/AMM的导航精度。

[1]KoifmanM,Bar-ItzhackIY.Inertialnavigationsystemaidedbyaircraftdynamics[J]. IEEE Trans.on Control Systems Technology, 1999,7(4):487-493.

[2]VasconcelosJF,SilvestreC,OliveiraP,etal.EmbeddedUAVmodelandLASERaidingtechniquesforinertialnavigationsystems[J].Control Engineering Practice,2010, 18:262-278.

[3]WangJH,GaoY.Landvehicledynamics-aidedinertialnavigation[J]. IEEE Trans.on Aerospace and Electronic Systems, 2010, 46(4): 1638-1653.

[4]MorgadoM,OliveiraP,SilvestreC,etal.Embeddedvehicledyna-micsaidingforUSBL/INSunderwaternavigationsystem[J]. IEEE Trans.on Control Systems Technology, 2014, 22(1): 322-330.

[5]LiN,DingW.Model-aidedstrapdowninertialnavigationintegratedmethodforAUVbasedonH∞filtering[C]∥Proc.of the IEEE International Conference on Computational and Information Sciences, 2013: 1088-1092.

[6] ØyvindH,EinarB,OddvarH.Model-aidedinertialnavigationforunderwatervehicles[C]∥Proc.of the IEEE International Conference on Robotics and Automation, 2008:1069-1076.

[7]FresconiF,HarkinsT.Aerodynamiccharacterizationsofasymmetricandmaneuvering105mm, 120mm,and155mmfin-stabilizedprojectilesderivedfromtelemetryexperiments[C]∥Proc.of the AIAA Atmospheric Flight Mechanics Conference, 2011: 1-30.

[8]FairfaxLD,FresconiF.Affordablestateestimationusinginertialnavigationsensorarrays[C]∥Proc.of the AIAA Atmospheric Flight Mechanics Conference, 2011:1-8.

[9]FairfaxLD,FresconiFE.Cost-efficientstateestimationforprecisionprojectiles[C]∥Proc.of the AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, 2011:1-11.

[10]LuoJJ,MaWH,YuanJP,etal. Principle and application of the integrated navigation[M].Xi’an:NorthwesternPolytechnicalUniversityPublisher,2012.(罗建军,马卫华,袁建平,等.组合导航原理与应用[M].西安:西北工业大学出版社,2012.)

[11]WuST,FeiYH. Flight control system[M].Beijing:BeijingUniversityofAeronauticsandAstronauticsPublisher,2005.(吴森堂,费玉华.飞行控制系统[M].北京:北京航空航天大学出版社,2005.)

[12]ShakedU,TheodorY.H∞-optimalestimation:atutorial[C]∥Proc.of the 31th IEEE Conference on Decision and Control, 1992:2278-2286.

[13]GaoYN,ChenJB,YangTP.Initialalignmentonmovingbaseforintegratednavigationsystembasedonrobustfilterapproach[J].Systems Engineering and Electronics, 2005,27(7):1260-1263. (高亚楠,陈家斌,杨亭鹏.基于鲁棒滤波的组合导航系统动基座对准[J].系统工程与电子技术,2005,27(7):1260-1263.)

[14]QinYY,ZhangHY,WangSH. Kalman filter and principle of integrated navigation[M].2nded.Xi’an:NorthwesternPolytechnicalUniversityPublisher,2011. (秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].2版.西安:西北工业大学出版社,2012.)

[15]WangX,ZhangSL,LiuMQ.ComparisonofKalmanfilter,H∞filterandrobustmixedKalman/H∞filter[C]∥Proc.of the 30th IEEE Chinese Control Conference,2011:3277-3281.

[16]GuillaumeJ,DucardJ. Fault-tolerant flight control and guidance systems-practical methods for small unmanned aerial vehicles[M].ChenZL,XieZGtrans.Beijing:NationalDefendIndustryPress,2012. (GuillaumeJ,DucardJ. 容错飞行控制与导航系统——小型无人机实用方法[M]. 陈自力,谢志刚译. 北京: 国防工业出版社,2012.)

[17]YiDJ.Robustfilteringforintegratednavigationsystem[D].Changsha:NationalUniversityofDefenseTechnology, 2008.(易大江.组合导航中的鲁棒滤波研究[D].长沙：国防科技大学，2008.)

Airborne integrated navigation technology of SINS/AMM based on extendedH∞filter

SHEN Jie-liang, WANG Yu, ZHU Xin-hua, SU Yan

(SchoolofMechanicalEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China)

The integrated navigation technology of aircraft motion model (AMM) with medium and low accuracy strapdown inertial navigation system (SINS) is studied. Considering the uncertainty of the system equation caused by inaccurate aerodynamic coefficient and the uncertainty of the observation equation as well as the noise, the extendedH∞filter (EHF) algorithm is proposed, which is abided by the min-max principle. The simulation, which is tested on a small fixed-wing UAV in both time and frequency domain, shows that for the SINS/AMM integrated navigation system, EHF performs better than the extended Kalman filter (EKF) in robustness and EHF brings approximately a 35% increasing in precision.

aircraft motion model (AMM); strapdown inertial navigation system (SINS); uncertainty of the system and the noise; extendedH∞filter (EHF)

2015-10-18;

2016-10-13;网络优先出版日期:2016-10-27。

国家自然科学基金(61374215)资助课题

V 249.3

10.3969/j.issn.1001-506X.2016.12.23

申杰亮(1989-),男,博士研究生,主要研究方向为组合导航技术。

E-mail:perfect.sjlchg2008@163.com

王宇(1978-),男,讲师,博士,主要研究方向为MEMS惯性导航、卫星导航、组合导航与控制。

E-mail:wangyu.njust@gmail.com

朱欣华(1963-),男,教授,博士,主要研究方向为导航制导与控制、嵌入式系统与应用、MEMS惯性技术。

E-mail:zhuxinhua@mail.njust.edu.cn