基于协作表示的雷达辐射源多传感器融合识别

周志文, 黄高明, 高 俊

(海军工程大学电子工程学院, 湖北 武汉 430033)



基于协作表示的雷达辐射源多传感器融合识别

周志文, 黄高明, 高 俊

(海军工程大学电子工程学院, 湖北 武汉 430033)

针对接收通道噪声影响和传感器引起的信号畸变,仅提高单传感器的识别性能远不能满足需求,提出了一种基于协作表示的雷达辐射源多传感器融合识别方法。首先,在训练阶段构成离线的完备字典,而多个传感器的接收信号在字典上求得协作表示系数及分类残差。接着通过设计合理的基本概率分配函数,将多传感器的分类残差与单元素事件的D-S理论相结合,根据最大信任决策规则得到融合识别结果。采用常见的6种雷达辐射源信号进行了仿真实验,仿真结果验证了提出方法的有效性,且较单传感器提高了识别性能,具有较好的噪声鲁棒性,适用于小样本的识别。

雷达辐射源识别; 协作表示; 决策级融合; D-S证据理论; 小样本问题

0 引 言

典型电子支援措施/雷达告警器的信号处理,包括信号探测、辐射源参数度量、数据库构建、信号分选与识别及作战提示，而这个过程的最终目的是对雷达信号分类从而识别作战环境中的敌方雷达、探知方位,估计威胁等级并上报信息。然而由于信号密度和电磁环境复杂度的增加、军事雷达类型的增多和分散以及噪声和传播影响导致信号特征错误或不完整,使得这个任务十分具有挑战性[1]。

雷达辐射源识别的两个关键技术为特征提取和分类器设计。在特征提取方面,高阶谱特征、时频原子[2]和小波包特征等均被作为新的特征量。文献[3]指出时频分析方法对于挖掘非平稳雷达信号的时变信息十分有利。文献[4-5]均采用了基于时频分布的辐射源特征提取,获得了较好的识别性能。在分类器设计方面,VNN[6]、粗糙集理论[7]和目前较为流行的稀疏分类[8-10](sparse classification, SC)都已应用在雷达辐射源识别中,同时协作表示[11-12](collaborative representation, CR)因其有效性和低计算复杂度逐渐受到关注。然而,噪声污染造成提取的特征量严重离散,类间特征发生重叠,从而影响了分类器的决策;不同传感器的特性引起接收信号畸变,使得时变信号的特征容易受到干扰,导致不能有效表征信号;对于有监督学习分类器,当辐射源训练样本较少,退化为小样本识别问题时,容易引起分类器性能严重下降。因此,单纯提高单分类器的识别能力或设计高性能的分类器已经无法满足实际需求,而融合多个传感器接收到的互补信息可以提高决策能力[13]。在多传感器数据融合中,D-S证据提供了一种度量每种状态不确定性的方法,在决策层融合多个传感器的识别结果,可以减小单个分类器的局限[14]。鉴于目前协作表示在辐射源识别领域较少应用,而它在计算复杂度、分类和解决小样本问题方面有着优异的性能,本文将CR引入到辐射源识别中,提出了基于CR的雷达辐射源多传感器融合识别算法(collaborative-representation-based multi-sensor fusion algorithm, CR-MSF)。对每个传感器的接收支路提取时频特征后,在离线的完备字典下求解协作表示系数,通过求得各类分类残差并设计合理的基本概率分配函数(basic probability assignment function, BPAF)赋予各类可信度,在D-S证据推理下融合得到决策级度量结果。仿真结果验证了本文提出算法的有效性,且较单传感器识别率更高,提高了系统鲁棒性能,且较适用于小样本条件下的雷达辐射源识别。

1 辐射源特征提取

1.1 雷达信号模型

每个接收通道中雷达实信号序列[15]可用如下数学形式表示:

s(t)=Re{uN(t)s[φ(t)]+n(t)}

(1)

1.2 基于时频分析的特征提取

如图1所示,传感器接收到的时域信号通过短时傅里叶变换(shorttimeFouriertransform,STFT)表示为二维时频分布。先对时频图像SSTFT(t,f)剪裁去除冗余信息,提取时频能量分布区域。接着将时频图通过如下公式进行映射:

p(u,v)=255×SSTFT(u,v)/max(SSTFT(u,v))

(2)

式中,1≤u≤U,1≤v≤V且U和V分别是剪裁后的图像尺寸。由于噪声分布在整个时频图像上且对应着灰度较低的高频成分,采用均值滤波减少噪声影响。最后将二维时频矩阵向量化为高维数据vec[p(u,v)]=z∈Rd,其中vec为向量化运算且d=U×V,并利用与数据不相关的随机投影[16](random projection, RP)降维得到低维特征向量,Rz=x∈Rr,其中R∈Rr×d为高斯压缩矩阵,r为降维后的维度。

图1 基于时频分析的特征提取流程图Fig.1 Flow chart of feature extraction based on time-frequency analysis

2 基于协作表示的辐射源融合识别

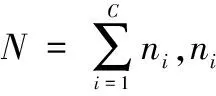
2.1 单传感器辐射源协作表示

由于不同类别的样本特征存在相似性,因而字典中这种原子类间的关联性可以协作表示测试样本,即其他类的样本有助于第i类样本的正确表示,这可以某种程度上解决小样本问题[11-12]。而对于新体制雷达辐射源的识别,截获到的信号往往十分有限甚至很少,因此是个典型的小样本问题,适用于协作表示的框架。假设测试样本属于第i类,即label(y)=i,则它可由Xi线性编码表示:

(3)

式中,αi=[αi,1,…,αi,ni]T∈Rni为编码系数;εi为编码误差。若在整个字典X上进行编码,则有

(4)

式中,α=[α1,…,αC]T为字典上的表示系数;ε=[ε1,…,εC]T为误差向量。那么对于协作表示分类,就是解决如下最小化问题：

(5)

(6)

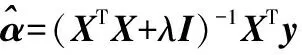
(7)

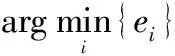
2.2 多传感器协作表示融合

然而,第2.1小节中单传感器的识别对分类残差只是简单地选择了最小值,而忽略了其他残差值的贡献。如图2所示,测试样本label(y)=4,但只有传感器2做出了合理的推断,这意味着对于正确分类选择最小值是合理的,但对于错误分类直接剔除其他残差值不利于做出正确的判断,因为传感器1中label(y)=4所对应的残差仅小于最小残差。然而,通过融合两个传感器的残差,最终可得到label(y)=4信任度较强的理论判据,这是由于单传感器非最小残差同样对正确识别提供着分类信息。因此融合多传感器的分类残差可以充分利用单传感器的分类信息和互补特性,从而对融合分类不确定性推理,减小单传感器的局限性。本小节在得到单传感器协作表示分类残差基础上,利用D-S证据理论对多传感器进行辐射源融合识别。

图2 两个传感器和融合后的分类残差示意图Fig.2 Classification residuals of two sensors and fusion

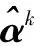
(8)

容易注意到,协作表示下的单传感器概率质量分配是个单元素事件集,即概率质量不是由联合命题或者不确定类分配的。对于本文的融合识别框架Ω,其焦点元素P={ci∈[1,2,…,C]},Ω上的子集即为对C类样本的判决。假设m为P上的基本概率赋值函数,且满足

(9)

式中,Φ为空集。因此,为满足基本概率分布上可信度和为1的条件,首先对处理后的残差归一化,得到每个传感器基本概率赋值函数为

(10)

步骤 1 利用D-S准则计算单元素事件的BPAF,其计算规则如下:

(11)

式中,cj,ct∈P。由于单元素集的特性,对于ci∩cj=Φ即意味着ci≠cj。那么对于融合矩阵,除了对角线上的元素其他全部为空集。然而,它并不满足条件(9)中第一个等式,所以需要对融合矩阵的概率再分配。

步骤 2 对非空集元素的概率质量再分配,计算公式如下：

(12)

式中,⊕表示直和;m(Φ)为上步所得空集命题的概率之和。那么对于K个传感器而言,同样在识别框架Ω下其D-S合成规则为

m(ct)=[m1⊕m2⊕…⊕mK](ct)

(13)

融合规则同样遵循前述两步。根据最大信任程度决策规则对最终的分类决策进行判决,则融合识别结果为最大概率值所对应的类别：

(14)

然而,在实际应用中,由于多传感器接收的辐射源信号相近,造成提取到的特征向量差异大不,并且各传感器的分类残差相关性较强,这样对于融合多传感器的互补信息和差异特性贡献较小。将式(6)的解代入到式(7)中,得

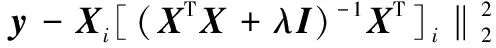
(15)

3 仿真实验

为验证本文基于协作表示的辐射源多传感器融合识别方法的有效性,仿真实验中采用了6类常见的雷达辐射源信号,包括常规脉冲(conventional pulse, CP)、线性调频(linear frequency modulation, LFM)、非线性余弦调频(nonlinear cosine frequency modulation, NCFM)、二相编码(binary phase shift keying, BPSK)、四相编码(quadrature phase shift keying, QPSK)和二频率编码(binary frequency shift keying, BFSK)信号。每类辐射源信号产生70个脉冲作为离线训练样本,降维后的特征维度r=90。由于r与计算复杂度、样本信号的冗余性相关,在仿真中选取了较为合适的值(其他值同样是可取的)。在相同参数设置条件下,实时产生测试样本。对于本文多传感器融合的仿真环境,每个接收通道的辐射源信号均在相同的信噪比(signal-to-noise ratio, SNR)下获得,每次进行1 000次蒙特卡罗仿真实验。

3.1 两个传感器融合识别性能

当SNR=-2 dB且接收信号同为CP时,两个传感器的正则化参数随机选择为λ1=0.2,λ2=0.4,在第2.1节所述协作表示下的两个单传感器分类残差如图3所示。

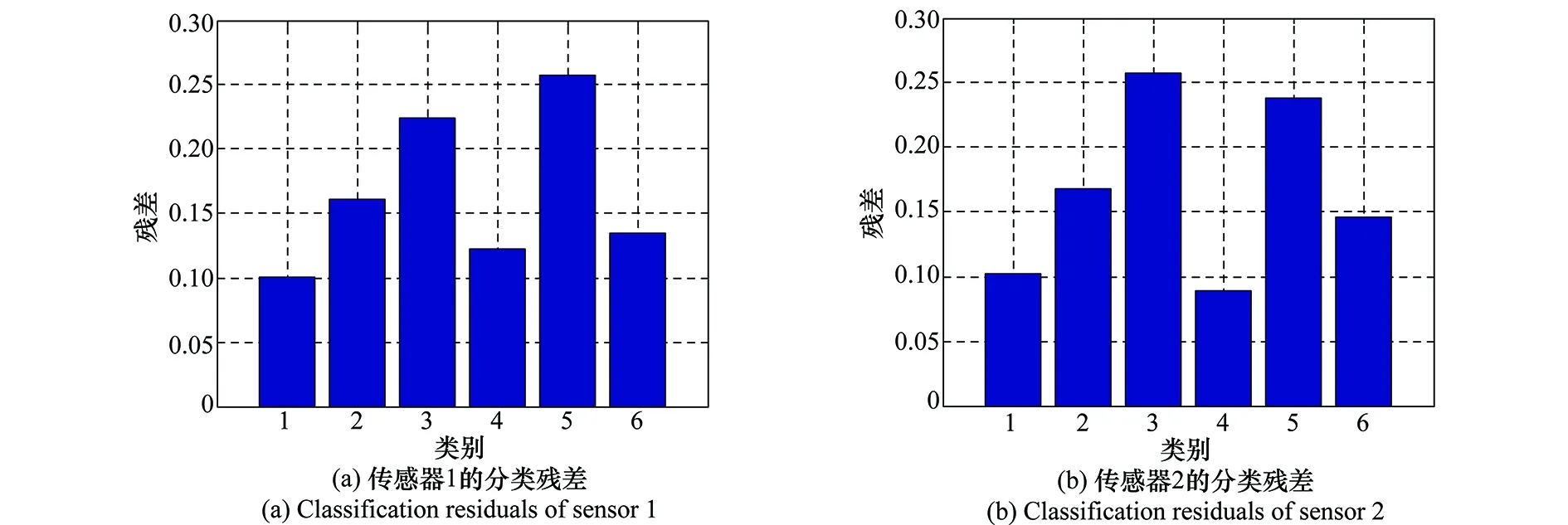
图3 两个传感器分类残差Fig.3 Classification residuals of two single sensors

由图3可以看出,接收噪声的影响以及分类器的差异,导致了两个传感器的分类残差不同,从而识别结果出现差异。若选择最小残差作为分类结果的判断依据,传感器1和传感器2的识别结果分别为CP(正确识别)和BPSK(错误识别)。在本文提出的算法框架下,求得两个传感器各焦点的概率质量,利用单命题D-S证据合成规则的概率分配如表1所示。

表1 两个传感器的概率质量分配

对比表1中数据可以看出：①尽管传感器2出现了误判,但仍对label(y)=1保持较高的可信度;②经融合后不仅纠正了传感器2的判定结果,而且对正确判决赋予了更高的概率质量。以最大后验概率作为广义置信度[18],则融合后对测试样本label(y)=1的信任程度明显大于单传感器,提高了正确分类置信度。下面对不同SNR条件下两个传感器融合识别性能仿真对比,其中训练字典保证n1=n2=…=nC=30共180个离线样本,不同SNR每类信号实时产生200个测试样本,识别性能采用正确识别率来衡量。

由图4可以看出:①随着SNR的提高,单传感器和融合后的正确识别率均逐渐增大,而且对于单传感器的协作表示识别,λ的选择影响着分类性能;②融合后的决策能力要优于单传感器,且相比SNR≥6 dB时,低SNR条件下性能提升更明显,这是因为当SNR≥6 dB时接收端信号相近且两个单传感器的识别性能已趋近稳健。

3.2 传感器数目对融合识别性能的影响

为对比不同传感器数目的融合识别性能,同时衡量多传感器的计算成本,在保持单传感器参数设置相同条件下进行仿真实验,并且记录不同传感器数目算法的运算时间。传感器数变化范围为K∈[2,7],不同接收支路的正则化参数随机选择,且满足0≤λk≤1,k∈[2,7]。由表2可以看出,随着传感器数的增加,计算时间不断增加且呈现线性关系,这说明提出的CR-MSF算法其计算成本主要在于单传感器的识别上。而图5表明:①当传感器数增加时,提出的融合算法识别率有一定的提高,但是当K>5时,性能提升得不再明显,几乎与K=5时相同;②在低信噪比条件下,经D-S证据融合后识别性能改善更加显著,但SNR≥0 dB时仅增大K并没有提高识别率,说明此时已充分利用了不同传感器的互补信息,制约识别性能的因素不再是传感器数,增大K反而会增加计算成本;③当SNR=-8 dB时,对于K∈[2,7]均能取得较高的融合识别率,说明CR-MSF算法在低信噪比条件下的鲁棒性较强,适用于高斯噪声环境下。

图4 不同SNR下融合识别性能Fig.4 Fusion performance with different SNRs

传感器数目K234567计算时间t/s601．8902．51204．51505．818082110．2

图5 传感器数与识别率关系的曲线图Fig.5 Relationship between the number of sensors and recognition rate

3.3 训练样本数目对融合识别性能的影响

从式(15)可以看出字典X影响着残差的表达,即X的完备性对测试样本的线性表征起着重要作用。下面针对训练样本数目与融合效果的关系进行了仿真实验,在其他参数设置相同的情况下改变每类训练样本数,仿真中保证n1=n2=…nC且ni∈[10,70]。

仿真结果如图6所示,由图可以看出:①随着每类样本数目的增加,不同信噪比条件下的识别率均有所提高,呈现递增的趋势,但当每类样本ni≥50时,识别性能改善得不再明显;②当样本数较少时,不同信噪比下的识别率区别显著,而当ni≥50时,融合后的噪声影响较小,这说明了字典的完备性对正确识别起着重要作用,尤其在低信噪比情况下;③当ni=10时,则此时字典X∈R90×60,即样本的维度大于样本数,是个小样本的识别问题。从图结果看出,提出CR-MSF算法仍能保持较高的识别率,说明了该算法框架适用于小样本情况下的辐射源识别。

图6 每类训练样本数目对融合识别的影响Fig.6 Effect on recognition performance with different training samples in each class

3.4 不同融合识别算法性能对比

下面,将本文提出的算法与不同融合识别算法进行对比分析。由于支撑向量机[19](support vector machine, SVM)在解决小样本、高维特征问题的优异性能,将概率SVM(probabilistic SVM, PSVM)与D-S证据相结合以对比本文的CR-MSF算法。同时,在提取相同的特征下,与文献[9]的信号级融合算法相比较。为对比小样本和样本充足条件下的算法性能,分别设置ni=10和ni=70进行仿真实验,仿真结果如表3所示。

从表3可以看出:①PSVM+DS和CR-MSF的决策级融合识别算法在两种样本情况下都优于文献[9]的信号级融合算法,这是由于原始数据端因噪声造成融合后的信号出现了差错,而无法在决策时纠错,但两种决策级融合算法会根据不同传感器的概率赋值调整权重值,从而减少了错误累加,提高了融合后的置信度;②尽管都为决策级融合算法,但CR-MSF在两种样本情况下识别率均优于PSVM+DS,说明单传感器的协作表示性能更优,且融合后的算法更适合解决小样本辐射源识别问题。

表3 不同算法融合识别性能对比

4 结 论

当接收通道存在噪声影响或因传感器特性引起信号畸变,仅提高单传感器的识别性能或设计优异的分类器已无法满足雷达辐射源识别实际需求,本文提出了一种基于协作表示的多传感器融合识别方法。构造了离线的完备字典后,将不同支路的接收信号在此字典下进行协作表示并求得残差,利用D-S证据理论对多传感器分类残差融合,最后得到决策层的判决结果。仿真结果验证了提出方法的有效性,提高了单传感器识别性能和正确判决的置信度,在低信噪比条件下鲁棒性较强,且与信号级和其他决策级融合算法相比,本文算法更适用于小样本的辐射源识别。

[1] Spezio A E. Electronic warfare systems[J].IEEETrans.onMicrowaveTheoryandTechniques, 2002, 50(3): 633-644.

[2] Zhu M, Pu Y W, Jin W D, et al. Feature extraction of radar emitter signals based on time-frequency atoms[J].ChineseJournalofRadioScience, 2007, 22(3): 458-462.

[3] Thayananthan T, Ljubisa S, Moeness A, et al. Time-frequency approach to radar detection, imaging, and classification[J].IETSignalProcessing, 2010, 4(4): 325-328.

[4] Bai H, Zhao Y J, Hu D X. Radar signal recognition based on the local binary pattern feature of time-frequency image[J].JournalofAstronautics,2013,34(1):139-146.(白航,赵拥军,胡德秀.时频图像局部二值模式特征在雷达信号分类识别中的应用[J].宇航学报,2013,34(1):139-146.)

[5] Zeng D, Zeng X, Lu G, et al. Automatic modulation classification of radar signals using the generalized time-frequency representation of Zhao, Atlas and Marks[J].IETRadar,SonarandNavigation, 2010, 5(4): 507-516.

[6] Shieh C S, Lin C T. A vector neural network for emitter identification[J].IEEETrans.onAntennasandPropagation, 2002, 50(8): 1120-1127.

[7] Guan X, Yi X, He Y. A novel emitter signal recognition model based on rough set[C]∥Proc.oftheLectureNotesinControlandInformationSciences, 2006, 345(1): 81-89.

[8] Ma J, Huang G M, Zuo W, et al. Robust radar waveform recognition algorithm based on random projections and sparse classification[J].IETRadar,SonarandNavigation,2014,8(4):290-296.

[9] Ma J, Huang G M, Ji J, et al. Signal-level fusion algorithm for radar emitter identification based on spare representation[J].ControlandDecision,2014,29(10):1798-1802.(马捷,黄高明,吉嘉,等.基于稀疏表示的雷达辐射源信号级融合识别算法[J].控制与决策,2014,29(10):1798-1802.)

[10] Wang L, Zhou L N, Ji H B, et al. A new matching pursuit algorithm for signal classification[J].JournalofElectronicsandInformationTechnology,2014,36(6):1329-1306.(王磊,周乐囡,姬红兵,等.一种面向信号分类的匹配追踪新方法[J].电子与信息学报,2014,36(6):1329-1306.)

[11] Jia S, Shen L L, Li Q Q. Gabor feature-based collaborative representation for hyperspectral imagery classification[J].IEEETrans.onGeoscienceandRemoteSensing, 2015, 53(2): 1118-1129.

[12] Li W, Du Q, Xiong M M. Kernel collaborative representation with Tikhonov regularization for hyperspectral image classification[J].IEEEGeoscienceandRemoteSensingLetters,2015,12(1):48-52.

[13] Alain A.Uncertaintytheoriesandmultisensorydatafusion[M]. Great Britain and United States: ISTE Ltd and Wiley, 2014: 4-28.

[14] Lawrence A K.Sensoranddatafusion:atoolforinformationassessmentanddecisionmaking[M]. Washington: SPIE Press, 2012: 183-232.

[15] Nadav L, Eli M.Radarsignals[M]. New York: Wiley, 2004: 53-68.

[16] Majumdar A, Ward R K. Robust classifiers for data reduced via random projections[J].IEEETrans.onSystems,Man,andCybernetics, 2010, 40(5): 1359-1371.

[17] Zhang X D.Matrixanalysisandapplications[M]. Beijing: Tsinghua University Press, 2013: 330-335.(张贤达. 矩阵分析与应用[M]. 北京:清华大学出版社, 2013: 330-335.)

[18] Li L, Ji H B. Radar emitter recognition based on multiple classifier fusion[J].JournalofDataAcquisitionandProcessing, 2010, 25(3): 396-400.(李林, 姬红兵. 一种基于多分类器融合的雷达辐射源识别方法[J]. 数据采集与处理, 2010, 25(3): 396-400.)

[19] Shi Y, Ji H B, Zhu M Z, et al. Specific radar emitter identification in multiple kernel fusion framework[J].JournalofElectronicsandInformationTechnology, 2014, 36(10): 2484-2490.(史亚,姬红兵,朱明哲,等.多核融合框架下的雷达辐射源个体识别[J].电子与信息学报,2014,36(10):2484-2490.)

Collaborative representation based radar emitter fusion recognition of multi-sensor

ZHOU Zhi-wen, HUANG Gao-ming, GAO Jun

(CollegeofElectronicEngineering,NavalUniversityofEngineering,Wuhan430033,China)

Aimed at the impact of noise in receiving channels and signal distortion caused by sensors, simply improving the recognition performance of a single sensor no long meeting the demands, a collaborative representation based radar emitter fusion recognition of multi-sensor method is proposed. Firstly, a completed dictionary is constructed with off-line sample signals in the training phase, on which collaborative coefficients of multiple receiving signals and classification residuals are obtained. Then, multi-sensor classification residuals and the D-S theory are combined by designing the basic probability assignment function reasonably, and consequently the fusion recognition result is acquired according to the maximum belief rule. Simulation experiments are performed by adopting 6 types of conventional radar emitters, the results validate the effectiveness of the proposed method and show that the method not only improves the performance in comparison with the single sensor, but is robust to noise and applicable to small-sample-size recognition.

radar emitter recognition; collaborative representation; decision-level fusion; D-S evidence theory; small-sample-size problem

2016-03-16;

2016-05-30;网络优先出版日期:2016-07-18。

国家高技术研究发展计划(863计划)(2014AA7014061)；国家自然科学基金(61501484)资助课题

TN 974

A

10.3969/j.issn.1001-506X.2016.12.07

周志文(1989-),男,博士研究生,主要研究方向为辐射源识别、信息融合。

E-mail:mini_paper@sina.com

黄高明(1972-),男,教授,博士研究生导师,主要研究方向为盲信号处理、无源探测。

E-mail:hgaom@126.com

高 俊(1957-),男,教授,博士研究生导师,主要研究方向为数字信号处理、数字通信技术。

E-mail:gaojunnj@163.com

网络优先出版地址:http:∥www.cnki.net/kcms/detail/11.2422.TN.20160718.1039.004.html