龙卷风风场下水面船舶倾覆的力学机理研究

贺沅平,危卫,顾兆林

(1.西安交通大学人居环境与建筑工程学院,710049,西安;2.武汉理工大学能源与动力工程学院,430070,武汉)



龙卷风风场下水面船舶倾覆的力学机理研究

贺沅平1,危卫2,顾兆林1

(1.西安交通大学人居环境与建筑工程学院,710049,西安;2.武汉理工大学能源与动力工程学院,430070,武汉)

为研究龙卷风风场对船舶稳定性的影响,利用龙卷风风场模型分析了船舶风荷载特性及其随方位的变化规律。龙卷风风场模型在柱坐标系下形成并假定流场定常,龙卷风的漏斗外形轴对称,且从外围到中心的气压降主要由切向风速产生的离心力来平衡;以“东方之星”船舶简化模型为例,计算了船舶的最小倾覆力矩,并从船舶航向以及船舶位于龙卷风风场的不同径向位置分析了船舶倾覆的力学条件。研究结果表明:船舶航向垂直于龙卷风的径向时,船两侧负压差大于最小倾覆力矩,从而导致船舶倾覆;船舶航向平行于龙卷风的径向时,船舶受高速风的冲击而发生倾覆,倾覆方向与龙卷风的切向一致;船舶航向与龙卷风风场径向成任意夹角时,倾覆取决于船舶相对于龙卷风中心的位置、龙卷风切向风速以及船舶航速。该结果可为船舶设计及龙卷风预警研究提供参考。

龙卷风;风荷载;“东方之星”游轮;船舶倾覆;预警

龙卷风风场特征与常规的大气边界层风完全不同,具有时间随机性、地域随机性及危害性,对此国内外学者采用理论分析和数值模拟等手段分析了龙卷风损坏陆面建筑的机理。Wen给出了三维风场模型来描述龙卷风的风速,并成功应用于高层建筑计算风载[1];Dutta等首次使用有限单元法(FEM)分别对高、低层建筑在龙卷风风场下的动态响应进行了研究[2];Eric等将龙卷风风场模型用于格勾式杆塔,探讨了龙卷风风载对杆塔稳定性的影响[3];McDonald等总结了影响龙卷风风阻设计的各因素,并针对核电厂当前设计标准分析了各因素的相关性[4];Sparks等通过对典型单层楼房屋顶风压差进行计算获得了所受风力,进而评估不同形式屋盖对龙卷风的抗风能力[5];宋拓等以核电常规岛主厂房钢框架结构为计算模型,分析了结构在不同龙卷风作用工况下的随机响应及可靠度[6]。但是,有关水龙卷对船舶稳定性的影响至今还未见相关研究。

基于“东方之星”游轮翻船事件,为更好地理解龙卷风风场对船舶稳定性的影响,本文以船舶简化模型为例,通过分析龙卷风风场特性及船舶位于龙卷风风场不同方位上的力学行为,证明了龙卷风风场的破坏性以及对龙卷风预警的必要性。

1 龙卷风风场模型及水面船舶风载荷

采用文献[1]给出的柱坐标系下三维风场模型来描述龙卷风的风速场,并从柱面坐标下的流体力学控制方程出发,完善了三维风场模型对气压场的描述,进而计算出龙卷风风场下水面船舶所受风荷载。

1.1 龙卷风的风场参数化模型

根据气流所处位置(坐标z值)不同,边界层将龙卷风风场气流分为上、下两部分,见图1,边界层以上(z>δ)气流各速度分量为

(1)

边界层内(z≤δ)气流各速度分量为

(2)

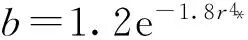
结合图1及式(1)、式(2)分析可知,龙卷风风场具有以下特征:①风场边界层分界面为零径向速度面,即边界层上部空间不存在径向速度分量,边界层内部切向速度沿高度由地面处零速度增大至峰值后逐渐减小,甚至在近龙卷风场核心区域出现径向出流;②切向速度随径向距离的增大呈先增大后减小的趋势,近龙卷风场核心区域边界层内部切向速度沿高度由地面处零速度增大至峰值后逐渐减小,至边界层上部时沿高度保持不变,龙卷风场远场处边界层内部切向速度沿高度增大但增速较缓,上部切向风速几乎不变,类似常态风剖面;③竖向速度变化无论沿径向还是沿高度均类似切向速度变化,但沿径向减小部分的衰减速度远大于切向速度。

图1 龙卷风特征参数示意图[1]

龙卷风的径向和垂直风速相对切向风速都较小,对建筑物影响远不及切向风速[7]。根据流体力学控制方程组,并假定流场定常且流场重力可以忽略、龙卷风的漏斗外形轴对称及龙卷风从外围到中心的气压降主要由切向风速产生的离心力来平衡[8],得到龙卷风的气压场

(3)

式中:Tmax(η)为高度z处的切向风速最大值;rmax(z)为高度z处Tmax(η)对应的径向坐标值。

1.2 龙卷风风场下水面船舶的荷载分析

船舶行驶过程遭遇龙卷风,下列原因可能引起船舶侧翻:①极高速风的冲击作用;②龙卷风中心横掠船舶时的气流压降导致船舶两侧负压产生差值。由于实际龙卷风风场对船舶的作用很复杂,为便于计算风荷载,本文进行了简化处理,把龙卷风风场下水面船舶上的风荷载简化成两部分:船舶左右两侧的气压差和风场冲击作用。

作用于船舶左右两侧的气压差为

(4)

式中:Δp(r)为船左侧气压降;Δp(r+B)为船右侧气压降;B为船宽。

高速风的冲击作用使得

(5)

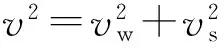
(6)

式中:Cp为压力系数;vs为船舶速度;vw为风速;v为相对速度;α为风速与船舶航向的法向之间的夹角。船舶速度、风速和相对速度的矢量关系如图2所示。

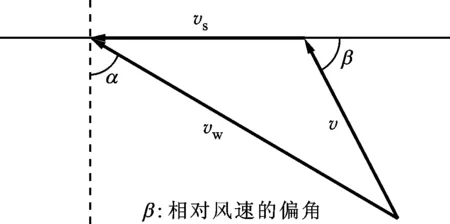
图2 风场的矢量速度

(7)

船舶行驶过程中遭遇龙卷风之后, 其在风场中的位置可由船舶中心距离龙卷风风场中心的距离和船舶行驶方向与龙卷风风场径向的夹角来描述。依据船舶行驶方向与龙卷风风场径向的夹角有2个典型方位,即:船舶行驶方向垂直于龙卷风的径向方向,如图3a所示,此时船舶上的风载荷仅受船舶两侧气压差的影响;船舶行驶方向沿着龙卷风的径向方向,如图3b所示,此时船舶上的风载荷仅受高速风的冲击。

(a)α=90°

(b)α=0°图3 船舶不同航向示意图

船舶行驶方向垂直于龙卷风的径向方向时,α=90°,此时导致船舶横向倾覆的风荷载仅为pP,即p1=pP=Δp(r)-Δp(r+B),根据式(1)～(4)可得

(8)

(9)

实际上,船舶在水面上航行经常受到突然作用的外力矩Mh,船舶在这种外力矩作用下很快发生倾斜。设Mq为船舶最小倾覆力矩,当Mh>Mq时,船舶会因倾覆力矩所做的功大于复原力矩所做的功而不再处于动平衡状态,进而导致倾覆[9]。

船舶所能承受的风压强Pf最大(Pf,max)时,其与最小倾覆力矩的关系为[10-11]

(10)

当船两侧荷载超过最大风压强时,船舶发生倾覆。

2 “东方之星”实例分析

2.1 最小倾覆力矩

2015年6月1日21时28分,从南京驶往重庆的“东方之星”游轮在长江中游湖北监利水域沉没,造成重大人员伤亡。根据雷达判断,事发当地附近出现12级以上龙卷风,但接地风力不大,约9.2 m/s,影响范围很小。“东方之星”游轮船长为76.5 m,总质量为2 200 t,船宽为11 m,船深为3.1 m,吃水深度为2.5 m左右,核定乘客定额为534人。2014年检验符合星级游轮评定标准,抗风标准10级。

本文分析中忽略轮船结构侧面及顶部一些细微而复杂的部分,将船舶近似为长方体,受风中心取露出水面侧面的中心位置,如图4所示。另外,由于“东方之星”经改造两侧被封闭,成为独立房间,为防止雨水飘入客舱必须关闭窗户,因此轮船可视为封闭结构。

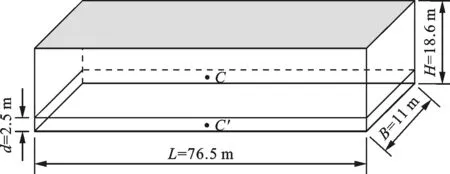
(a)结构图

(b)实体图图4 “东方之星”结构示意图

分析龙卷风风场水面船舶倾覆的可能性时,首先要获得“东方之星”自身的倾覆力矩。倾覆力矩不仅与船舶的质量及尺寸有关,还涉及船舶重心和浮心的具体位置。由于影响这两者的因素不能精确获得,如船舶装载状态、航区、船内重物移动、自由液面等等,所以下面根据“东方之星”船检的抗风等级估算出它的最小倾覆力矩Mq。

根据蒲式风级与风压对照表(气象仪器http:∥www.98cns.com/qxyq/feng.htm),得知最小风压范围为37.52～50.41 N/m2,由此可以得出该船的最小倾覆力矩。计算步骤如下:

受风面积

(11)

受风面积中心距船舶1/2吃水的距离

(12)

最小倾覆力矩

Mq=Pf,maxAfZf

(13)

代入已知数据,得“东方之星”最小倾覆力矩为Mq=4.27×105～5.74×105N·m。

2.2 龙卷风风场中船舶倾覆的区域分析

根据雷达判断,事发当地附近的确出现风力为12级(F2)的龙卷风,此时船舶进入风场危险区域将发生倾覆。根据特征参数表1,可得Vmax=52.4 m/s,rmax=50.0 m。另外,Pf,max=50.41 N/m2,Zf=9.3 m,B=11 m,ρ=1.29 kg/m3。

表1 3种等级(F1、F2、F3)龙卷风的特征参数[7]

注:V为龙卷风的平移速度;Umax为龙卷风场的最大速度,Umax=Vmax+V;Δpmax为龙卷风风场的最大气压降。

在龙卷风风场不同区域下船舶倾覆倾向的分析如下。

(1)船舶行驶方向垂直于龙卷风的径向方向(α=90°),此时“东方之星”行驶方向与最大风速的切向相同,如图3a所示。由船舶两侧压强|Pf|=|Pf,max|可得r*1=0.853 2,r*2=0.940 1,r*3=3.018 4,即r1=42.66 m,r2=47.01 m,r3=150.92 m,如图5所示。船舶恰好处于龙卷风风场中心时,各侧面风压具有一致性,船舶只可能发生膨胀爆炸式破坏;距离龙卷风核心半径0～r1和r2～r3位置时,船舶会因船两侧负压差大于最小倾覆力矩而发生倾覆,且在λ1区域船舶将往龙卷风中心倾覆,在λ3区域船舶倾覆方向背离龙卷风中心;在r1～r2以及r3以外范围,船舶在相对较小的外力矩及本身的回复力矩的作用下发生摇摆,但不会倾覆。

图5 α=90°时船舶倾覆区域

(2)船舶行驶方向沿着龙卷风的径向(α=0°),此时“东方之星”的航向如图3b所示,Cp=0.72[12]。由船舶两侧压差|Pf|sinβ=|Pf,max|(β为相对风速的偏角),可得r*4=0.111 7,r*5=7.190 6,即r4=5.585 m,r5=359.53 m,如图6所示。在距离龙卷风核心半径r4～r5位置时,船舶会因高速风的冲击发生倾覆,倾覆方向与切向风一致。

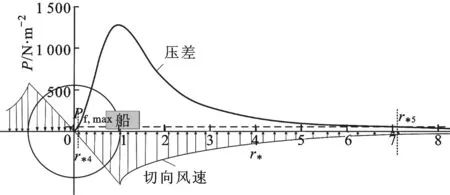
图6 α=0°时船舶倾覆区域

(3)船舶行驶方向为任意角度,即航向与龙卷风风场径向成任意夹角时,船舶将受到两侧负压差及高速风冲击的共同作用,因此在龙卷风强度一定的情况下,倾覆主要取决于距离龙卷风中心的径向距离、船舶航速大小及方向。结合图5、6,在λ1区域(0～r1)及λ3区域(r2～r3),船舶沿任意方向行驶必遭倾覆;在λ2区域(r1～r2),船舶沿不同方向行驶均受到横向风压的作用,见图7,当α趋近0°时倾覆速度较快,当α接近90°的小范围内时船舶所受风压小于它的最小倾覆力矩对应的风压,此时船舶不会倾覆;在λ4区域(r3～r5),见图8,当α接近90°时船舶所受风压小于它的最小倾覆力矩对应的风压,通过减少α有机会避免横向倾覆。事实上,龙卷风移动方向多变,船舶不断摇摆,航向基本无法控制在小范围内,因此处在λ2、λ4区域船舶也基本难以避免倾覆厄运。

另外,龙卷风具有快速移动、方向多变以及破坏力强等特性,所以处于龙卷风影响范围内的船舶难以控制[13]。水面波浪也会引起船舶横摇,特别是在恶劣海况时,船舶做大幅横摇运动并表现出复杂的非线性动力学行为[14]。在龙卷风作用以及波浪外激励下,严重的非线性横摇运动使船舶更易倾覆。

图7 船舶在λ2区域(r1～r2)不同航向时的横向风压

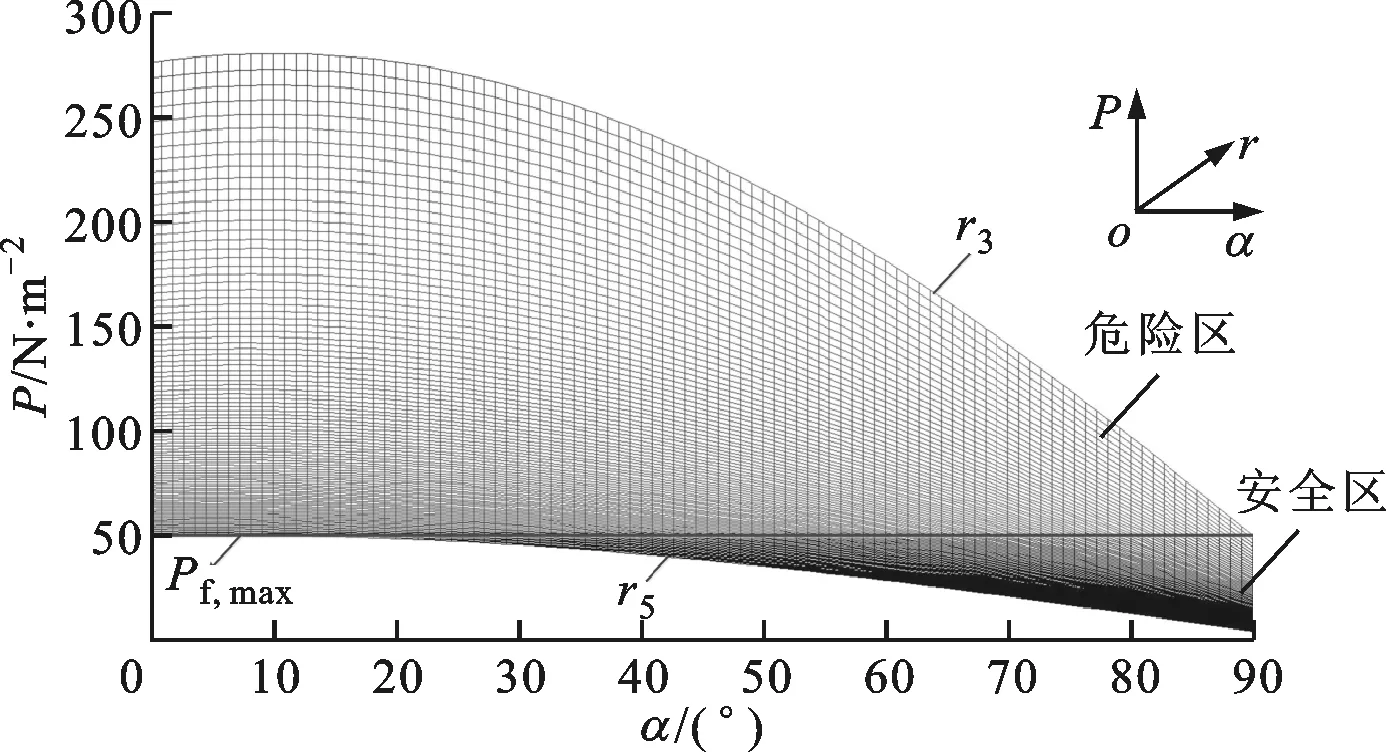
图8 船舶在λ4区域(r3～r5)不同航向时的横向风压

3 结 论

本文从流体力学控制方程出发,完善了三维龙卷风风场模型对气压场的描述,有助于准确计算龙卷风风场下水面船舶所受风荷载。根据龙卷风风场模型以及水面航行船舶倾覆力学机理,讨论了龙卷风风场下船舶在水面航行的力学行为,其力学特征与船舶位于龙卷风风场中心的径向距离以及船舶航向与径向的角度紧密相关,导致倾覆的风压大小主要取决于船舶相对于龙卷风中心的位置、龙卷风切向风速以及船舶航速。龙卷风具有快速移动、方向多变以及破坏力强等特性,处于龙卷风影响范围内的船舶难以控制,加上水面波浪引起的船舶横摇,极易导致船舶的倾覆。因此,加强预报系统的定位精确性和时间超前性更具实际意义。

[1] WEN Y K. Dynamic tornadic wind loads on tall buildings [J]. Journal of the Structural Division, 1975, 101(1): 169-185.

[2] DUTTA P K, GHOSH A K, AGARWAL B L. Dynamic response of structures subjected to tornado loads by FEM [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(1): 55-69.

[3] SAVORY E. Modelling of tornado and icroburst-induced wind loading and failure of a lattice transmission tower [J]. Engineering Structures, 2001, 23(4): 365-375.

[4] MCDONALD J R, MEHTA K C, MINOR J E. Tornado-resistant design of nuclear power-plant structures [J]. Nuclear Safety, 1973, 15(4): 432-439.

[5] SPARKS P R. On the failure of single-story ood-framed houses in severe storms [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1988, 29(1/2/3): 245-252.

[6] 宋拓, 吕令毅. 龙卷风作用核电常规岛主厂房随机响应及结构体系可靠度 [J]. 建筑结构学报, 2014, 35(5): 128-134. SONG Tuo, LÜ Lingyi. Stochastic response and structure reliability of nuclear power plant main house under tornado loads [J]. Journal of Building Structure, 2014, 35(5): 128-134.

[7] 徐枫, 肖仪清, 李波, 等. 龙卷风风场特性的CFD数值模拟 [J]. 空气动力学学报, 2013, 31(3): 350-370. XIAO Feng, XIAO Yiqing, LI Bo, et al. CFD numerical simulation of wind field characteristics of tornado [J]. Acta Aerodynamica Sinica, 2013, 31(3): 350-370.

[8] 汤卓, 张源, 吕令毅. 龙卷风风场模型及风荷载研究 [J]. 建筑结构学报, 2012, 33(3): 104-105. TANG Zhuo, ZHANG Yuan, LÜ Lingyi. Study on tornado model and tornado-induced wind loads [J]. Journal of Building Structure, 2012, 33(3): 104-105.

[9] 刘红. 船舶原理 [M]. 上海: 上海交通大学出版社, 2009.

[10]方学智. 船舶设计原理 [M]. 北京: 清华大学出版社, 2014: 138-176.

[11]刘亚冲, 胡安康, 韩凤磊, 等. 超大型集装箱船风载荷系数研究 [J]. 武汉理工大学学报, 2014, 36(4): 80-85.

LIU Y C, HU A K, HAN F L, et al. Research on wind load coefficients of large scale container ship [J]. Journal of Wuhan University of Technology, 2014, 36(4): 80-85.

[12]陆冠东. 列车强侧向风力作用下的倾覆力矩 [J]. 铁道车辆, 2008, 46(9): 9-10. LIU Guandong. Capsizing moment of train under strong lateral wind [J]. Railway Vehicle, 2008, 46(9): 9-10.

[13]JOSEPH E T, DANIELLE N, BRENDA P, et al. Tornadoes, social science, and the false alarm effect [J]. Weather Climate and Society, 2015, 7(4): 333-351.

[14]SPYROU K J, THOMPSON J M T. The nonlinear dynamics of ship motions: a field overview and some recent developments [J]. Philosophical Transactions: Mathematical, Physical and Engineering Sciences, 2000, 358(1771): 1735-1760.

[本刊相关文献链接]

李乃一,彭宗仁,刘鹏.直流电压下环氧浇注绝缘子的表面电场分析.2016,50(2):73-79.[doi:10.7652/xjtuxb201602013]

李远洁,江凯,刘子龙.低温增强型非晶铟镓锌氧薄膜晶体管特性研究.2015,49(12):1-5.[doi:10.7652/xjtuxb201512 001]

李春艳,高忠权,刘兵,等.电极位置与电极面积对离子电流影响的试验研究.2015,49(7):55-60.[doi:10.7652/xjtuxb 201507010]

马利娥,梅雪松,李彦锋,等.薄膜传输系统导向辊的力学特性分析.2014,48(11):86-91.[doi:10.7652/xjtuxb201411 015]

(编辑 苗凌)

Aerodynamic Forces on a Ship in Tornado and Their Impact on Ship Capsizing

HE Yuanping1,WEI Wei2,GU Zhaolin1

(1. School of Human Settlements and Civil Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. School of Energy and Power Engineering, Wuhan University of Technology, Wuhan 430070, China)

To investigate the impacts of tornado wind field on ship stability, the characteristics of wind loads on the ship and ship capsizing law are analyzed. A tornado wind field model is constructed on cylindrical coordinates, the flow field of the tornado is supposed as steady and the tornado funnel as axisymmetric in its shape. The air pressure drop from the tornado periphery to its center is assumed to be mainly balanced by the centrifugal force derived from tangential velocity of tornado. Taking simplified Eastern Star ship model as an example, the minimum overturning moment of the suffering ship is evaluated, and the tornado’s aerodynamic impact on ship capsizing is analyzed considering the vessel sailing directions and different radial positions of the field where the vessel is located. According to the results, when sailing direction is perpendicular to the radial direction of the tornado, the ship capsizes as the pressure difference between both ship sides gets greater than its minimum overturning moment; when sailing along the radial direction, mainly due to dynamic impacts of high-speed incoming wind, the ship capsizes in the tangential direction of the tornado; when the ship sails in any direction, whether the ship capsizes depends on the ship’s radial distance from the tornado center, the tangential wind speed of the tornado and the ship velocity. This results may provide a reference for ship design and tornado-warning research.

tornado; wind load; Eastern Star ship; ship capsizing; tornado-warning

10.7652/xjtuxb201605018

2015-11-03。 作者简介:贺沅平(1991—),女,博士生;顾兆林(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(40675011,10872159)。

时间:2016-03-01

http:∥www.cnki.net/kcms/detail/61.1069.T.20160301.1014.002.html

O355,U661.3

A

0253-987X(2016)05-0120-05