大型薄壁件多点定位的初始布局优化算法研究

王少锋,洪军,王建国,李宝童,杨朝晖

(1.内蒙古科技大学机械工程学院,014010,内蒙古包头;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安;3.西北工业大学航空学院,710072,西安)



大型薄壁件多点定位的初始布局优化算法研究

王少锋1,2,洪军2,王建国1,李宝童2,杨朝晖3

(1.内蒙古科技大学机械工程学院,014010,内蒙古包头;2.西安交通大学机械制造系统工程国家重点实验室,710049,西安;3.西北工业大学航空学院,710072,西安)

为了抑制大型薄壁件加工过程中传统“N-2-1”定位原理的支承/定位能力局部失效的现象,以满足工件夹紧力和外形定位精度为目标,并基于支承/定位资源约束,提出了跟随加工区域布置定位点的“X-2-1”多点支承/定位方法,该方法不仅能保证工件加工过程中的夹持可靠性,而且能实现对工件不同加工区域定位误差有针对性的重点防控。实验结果表明:使用该方法计算得到的工件最大定位误差小于0.2 mm,远远优于传统均布支承/定位点在相同实验条件下实验件0.8 mm的最大定位误差,从而抑制了工件外形定位误差对加工质量的扰动。提出的支承/定位点初始布局方案可为进一步的全局优化,并以此控制工件加工变形、提高工艺系统刚度,最终改善加工质量奠定基础。

薄壁件;多点定位;初始布局

弱刚度薄壳类零件在自重与外部载荷的作用下,易产生法向变形,传统“3-2-1”六点定位原理无法实现工件的完全定位。鉴于此,Cai等提出了“N-2-1”定位原理[1],但其并不适用于切边等工艺,原因在于部分支承/定位点的逐渐失效导致相应加工区域刚度减弱。为此,Hu等提出了“X-2-1”动态定位原理[2-3],但从目前已查阅文献的内容看,该理论对于如何寻找最优X的研究还不够充分。

传统的装夹方案依赖于直观判断和经验的积累,或者有针对性地对工件弱刚度部位进行加固。其缺陷在于:经验的获取不能满足加工质量的不断发展;弱刚度部位的针对性加固需长时间地尝试和调整。为此,大量的研究围绕着工件装夹定位布局的优化展开。King等构建了工夹系统的刚性体模型,利用非线性优化技术优化工件静态装夹定位布局[4];DeMeter继承了文献[4]的研究成果,并进一步约束了装夹定位布局优化过程中的夹紧力[5];Menassa等基于有限元分析对装夹定位布局优化进行了研究[6],优化目标被设计为最小化加工位置处的结点变形总和;Cai等延伸了文献[6]的研究工作,更合理地设置最小化工件法向变形的平方和为优化目标[1];文献[7-8]也类似地实现了所关注局部结点变形的最小化分析。由此可看出,上述方法的研究具有设计变量的目标函数不明确、最终布局方案的获取对优化过程的初值异常敏感等缺点。

上述方法只是对以往方法的改进,而不是全局最优方案。为此,本课题组前期基于数值计算探索了大型薄壁件定位参数对其定位精度的影响规律[9],而本文拓展了上述研究工作。以满足工件夹紧力和外形定位精度为目标,并基于定位资源(支承/定位点数量)约束,提出一种跟随加工区域布置定位点的多点支承/定位方法,旨在保证在工件可靠装夹的前提下,高效利用有限的定位资源,实现对工件多点支承/定位参数的优化,为进一步控制工件加工变形、提高工艺系统刚度为目标的定位点布局全局优化提供可靠的初值。

1 “X-2-1”跟随定位原理

定位的目的是使工件在夹具中相对机床、刀具具有确定的位姿。现有“N-2-1”定位原理无法抑制弱刚度空间薄壁工件切边过程中动态变化的支承/定位点数量所带来的夹紧力和定位精度的缺失。

针对上述有效支承/定位点随切边路径动态变化的问题,并受文献[2-3]的启发,本文提出一种具有新含义的“X-2-1”跟随定位原理,如图1所示,“X”代表在第一基准面上为保障薄壁工件加工区域定位精度而布置的支承/定位点数量;“2”和“1”分别代表在第2、3基准面上相应布置2个、1个支承/定位点。该定位方法不仅限制了薄壁件的所有自由度,而且能够集中有限定位资源,于第一基准面上有针对性地在各加工区域合理布置“X”个支承/定位点,以此在满足加工过程对夹紧力需求的前提下,实现最小化工件加工区域定位误差δ的目的。

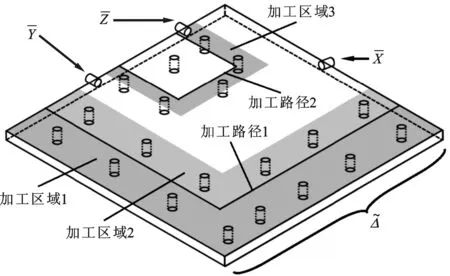
图1 “X-2-1”跟随定位原理

2 多支承/定位点柔性工装

综合考虑大型薄壁件的几何特性及其加工特殊性,为实现其可靠装夹与精确定位,设计了支承/定位阵列工装原型,如图2所示;提出了x和y坐标集中调整、z坐标单独调整方案;确定了支承/定位球半径r=20 mm,吸盘直径r=80 mm,滑枕数m=10,各滑枕上支承/定位单元数n=2,相邻两滑枕上支承/定位点沿x方向的最小间距极限值Dx_min=150 mm,同一滑枕上相邻两个支承/定位点沿y方向的最小间距极限值Dy_min=150 mm。

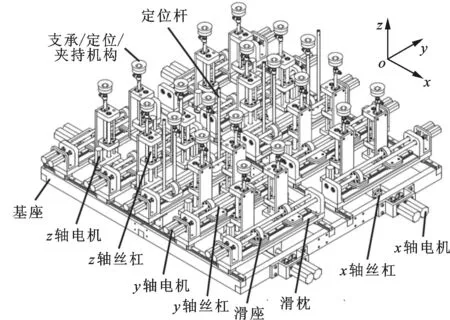
图2 多点柔性支承/定位阵列工装原型

图2所示工装原型主要由基座、滑枕、滑座、支承/定位单元、真空夹持末端等组成,采用单侧真空吸附实现工件夹紧。基座上装有10个滑枕,可沿x轴移动;各滑枕上装有2个滑座,可沿y轴移动;各滑座上装有1个支承/定位单元,可带动顶端真空夹持末端机构沿z轴运动,利用内置球头相切工件支承面完成工件定位。

3 支承/定位点跟随定位算法

控制加工质量的前提是提供足够的夹紧力,以保障工件装夹的可靠性,同时抑制工件定位误差对加工质量的干扰,可直接通过提高工件外形定位精度实现。依据加工路径将工件支承面分割为加工和非加工区域,优先在加工区域添加支承/定位点,在达到工件对夹紧力要求的前提下,进一步以满足工件外形精度为目标添加支承/定位点,直至达到支承/定位资源极限,由此确定所需支承/定位点的数量。此外,为实现以削弱工件最大定位误差提高工件定位精度的目的,选取最大定位误差位置添加支承/定位点,可得到满足工件夹紧力、定位误差约束的初始装夹方案。

基于上述思路,跟随加工区域的支承/定位点布置流程可表述为如下优化问题:

在总定位资源Nmax的约束下,求解各加工区域的支承/定位方案,即各支承/定位点位置P1,P2,…,达到工件对夹紧力需求FJ_max的前提下,削弱工件定位误差,以此控制工件外形精度,数学描述为

目标函数 min(δ)=f(P1,P2,…)

约束条件N≤Nmax,FJ≥FJ_min

优化过程实现的具体步骤如下。

(1)设置最大支承/定位点数量Nmax,设置支承/定位点初始分布P1,P2,…,PN,跟随加工路径划分工件支承面为n个加工区域。

(2)构建基于支承/定位点分布P1,P2,…,P的工件多点定位误差数值分析模型。

(3)求解并提取施加于工件上的夹紧力总和FJ与加工区域i的最大变形量δi_max,i=1,…,n。

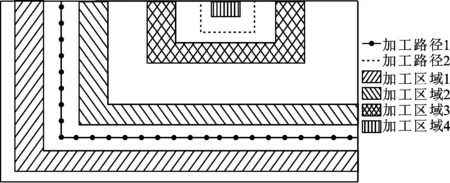
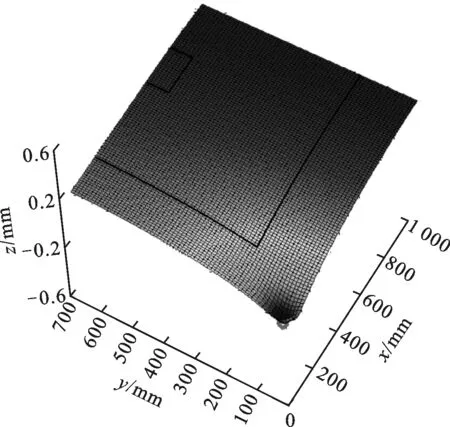
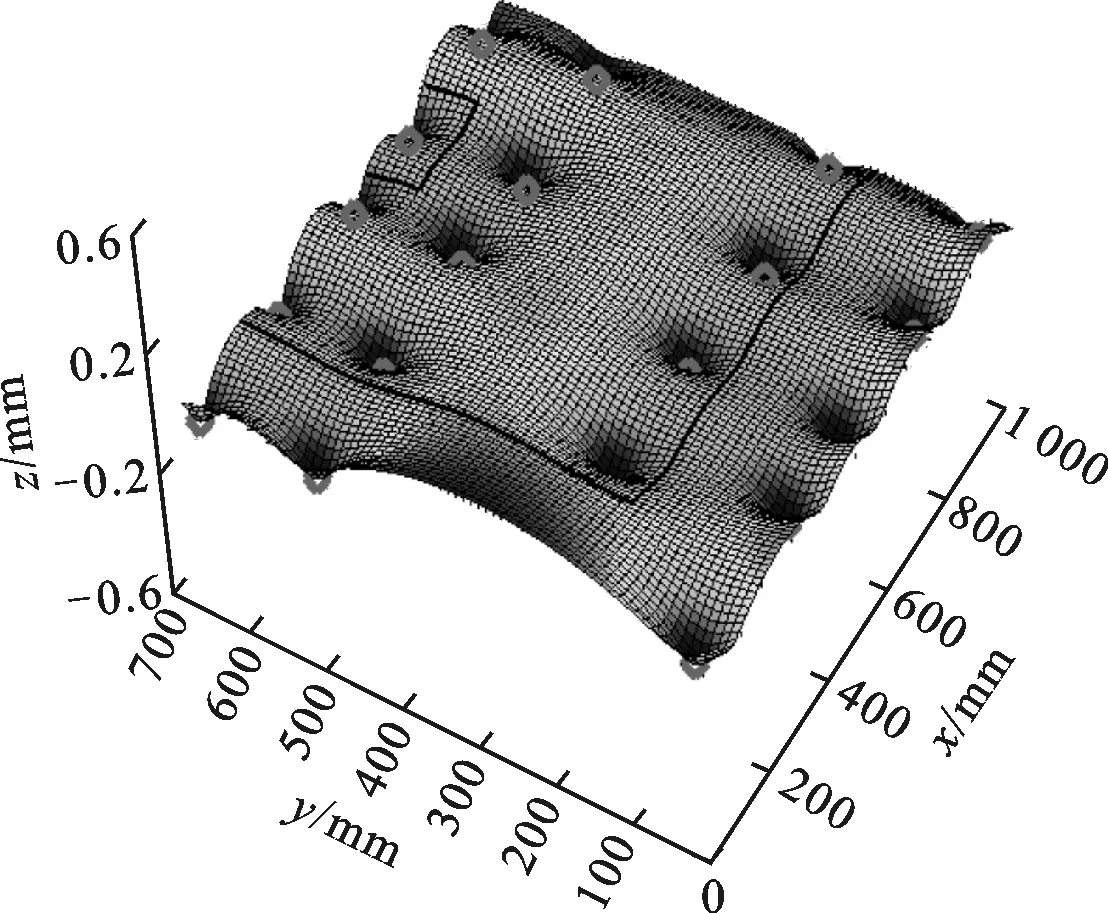
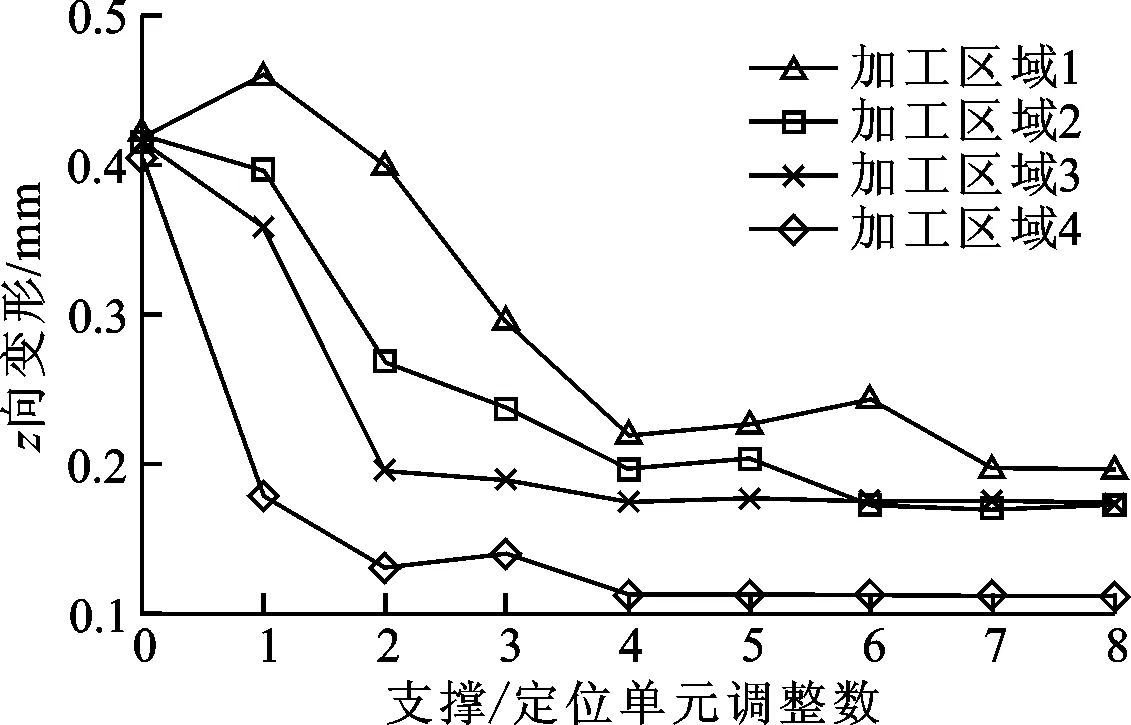
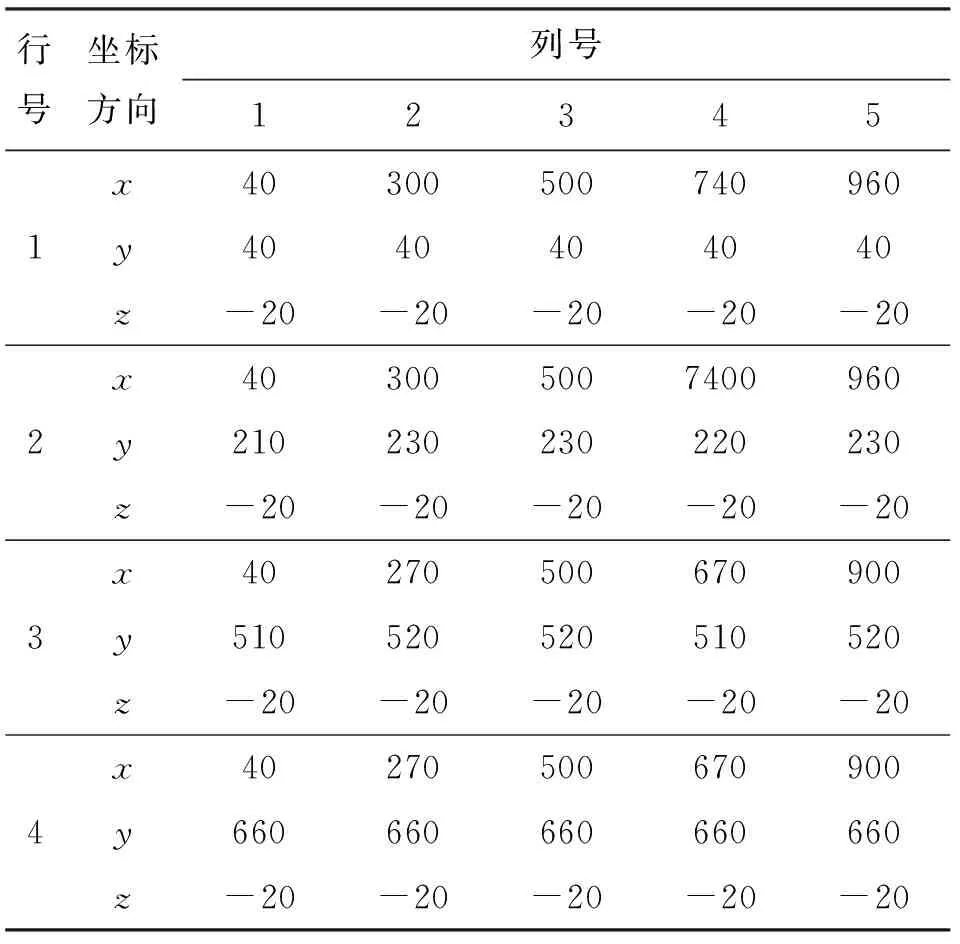
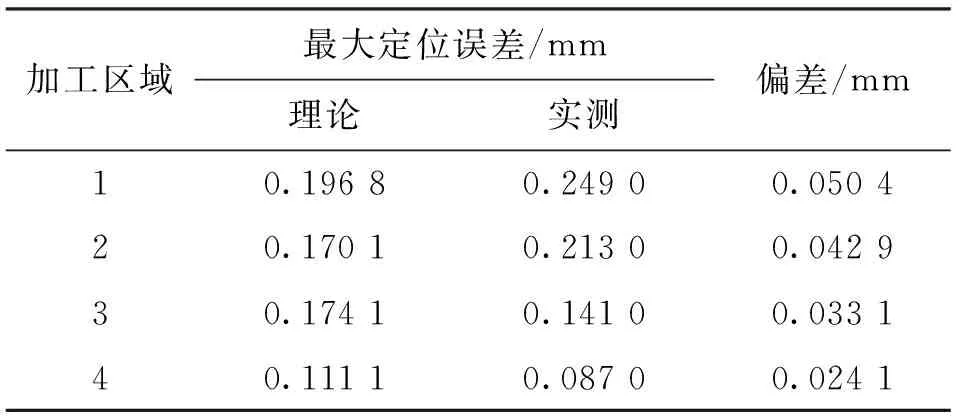
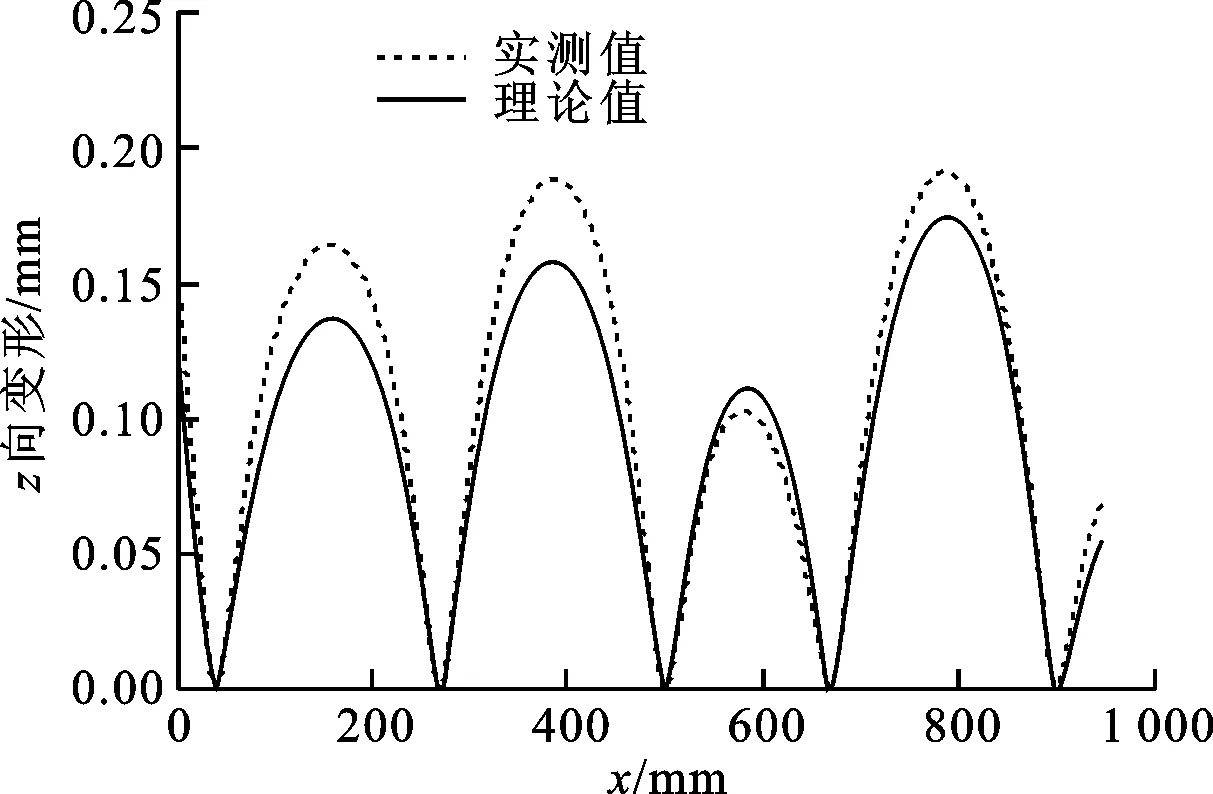
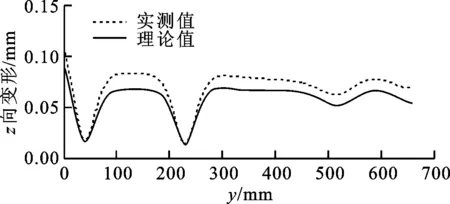
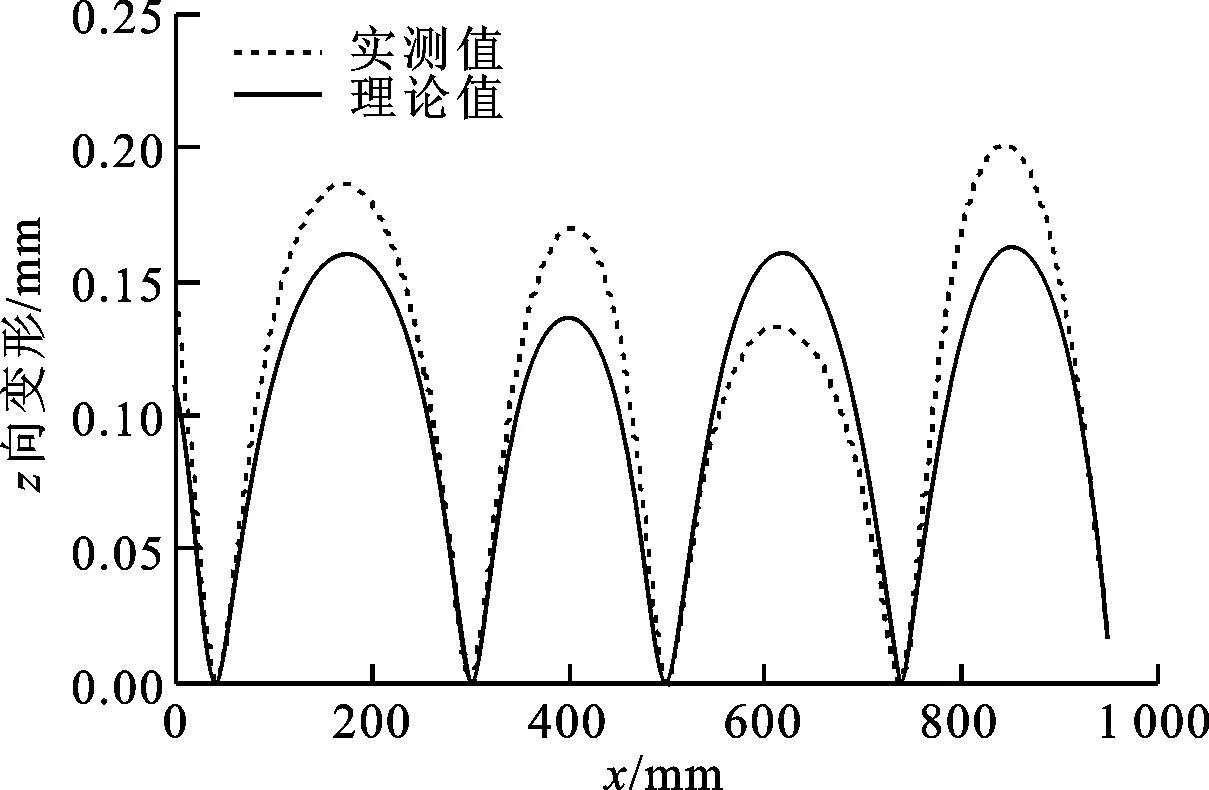
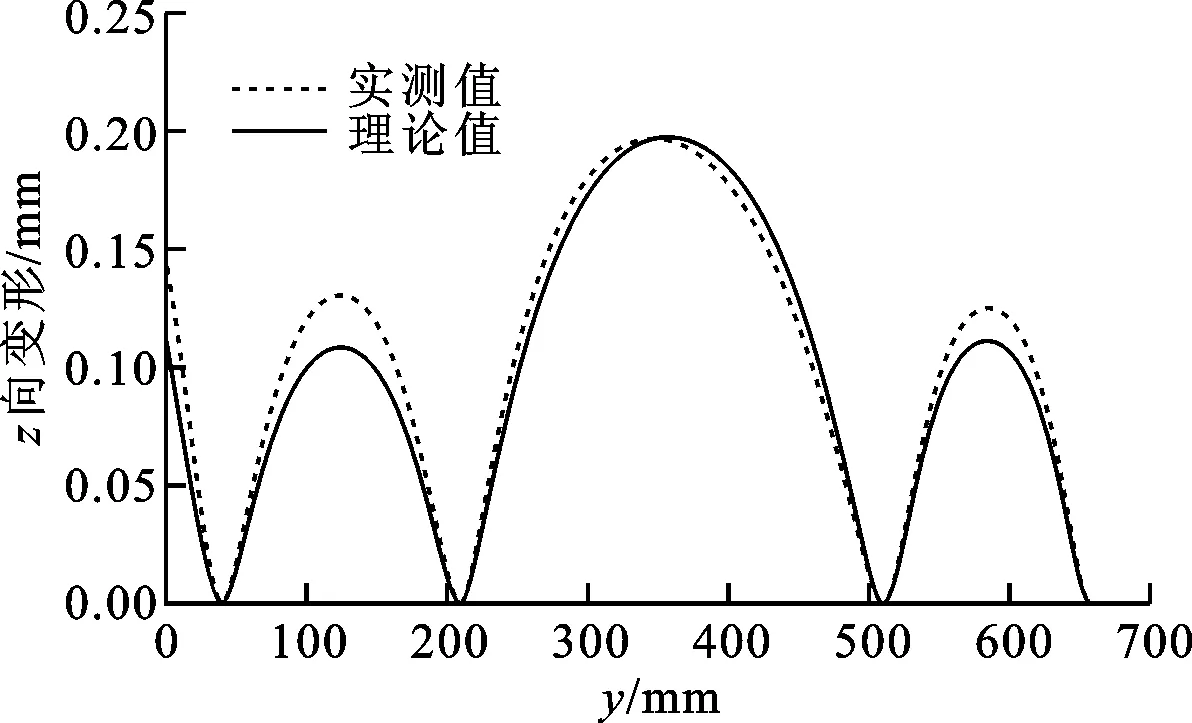
(4)若FJ≥FJ_min,表明工件满足夹紧力需求,转至步骤(5);若FJ

(5)若δi_max≤δmax,表明满足工件加工区域i外形定位误差约束。令i=i+1,若i>n,表明当前定位点分布下,对所有加工区域的分析已结束,且符合工件对夹紧力和外形精度的需求,故退出计算;否则,返回步骤(3)。若δi_max>δmax,表明不满足工件加工区域i外形定位误差约束。令N=N+1,并在δi_max处添加支承/定位点。若新增支承/定位点PN满足其间距约束,则确定在该区域添加,转至步骤(6);否则,不在该区域添加,并令N=N-1,转至步骤(6)。

(6)若N>Nmax,表明已超出支承/定位资源约束,退出计算;否则,令i=i+1,若i>n,表明当前支承/定位点分布下,对所有加工区域的分析已结束,更新定位点分布,并令i=1,返回步骤(2),否则,返回步骤(3)。

4 算例研究

本节选择工程中常见的平面大型薄壁件多点定位过程为算例,说明跟随加工区域的多点定位过程,并且在保证工件加工过程中夹持可靠的前提下,展示该方法对工件不同加工区域定位误差有针对性重点防控的特性。与本课题组所设计的多点柔性支承/定位阵列工装进行实验测试,讨论分析理论与实验结果差异,进一步验证工装原型设计与相应定位方法的正确性、合理性。

图3所示为待分析的平面大型薄壁件,外形尺寸为1 920 mm×1 320 mm,厚度为3 mm,材料为7075铝合金,弹性模量Ewp为70 GPa,要求提供的夹紧力为5 600 N,且需加工出周边轮廓,并开两矩形窗口。依据对称性,取四分之一为研究对象,沿加工路径确定,如图3所示4个加工区域,同时采用Shell 181壳单元,构建有限元数值分析模型,真空法向吸附力为0.05 N/mm2。由此可知,四分之一工件需提供1 400 N夹紧力,并且需保证工件外形精度δmax在[-0.2 mm, 0.2 mm]范围内。

图3 平面大型薄壁工件样件

4.1 理论计算分析

4.1.1 跟随加工区域的多点支承/定位历程 基于多点支承/定位算法,可得图3所示工件的支承/定位点添加历程,如图4～9所示。图10显示了工件支承/定位点添加过程中各加工区域最大定位误差的变化趋势。图4显示了初始支承/定位点分布下工件表面z向变形。于各加工区域最大变形位置添加支承/定位点,图5显示了第1次添加后的工件外形。

图4 多点定位过程:初始支承/定位分布

图5 多点定位过程:第1次添加定位点

图6 多点定位过程:第2次添加定位点

图6显示了第2次添加过程。若各加工区域均添加支承/定位点,夹紧力总和FJ(600 N)不满足工件需求FJ_min(1 400 N),故应在各加工区域添加支承/定位点,然而在对加工区域4的添加过程中,无法搜索到符合支承/定位点间距约束的位置,本次添加过程未在加工区域4进行。类似地,图7所示的第5次添加过程未在加工区域3进行。

图7 多点定位过程:第5次添加定位点

如图8所示,第6次添加后夹紧力总和达到1 425 N,满足加工需求。因此,第7次添加过程在加工区域1、2进行,同时发现加工区域2的最大定位误差δ2_max(0.170 8 mm)满足工件外形精度要求,故第7次添加过程不再选择对加工区域2进行添加,而加工区域1的最大定位误差δ1_max(0.244 8 mm)不满足要求,故第7次添加仅选择在该区域中进行。如图9所示,第7次添加后,支承/定位点数目达到极限,故支承/定位点添加过程结束。

图8 多点定位过程:第6次添加定位点

图9 多点定位过程:第7次添加定位点

经计算可知,夹紧力总和满足工件需求,加工区域1的最大定位误差δ1_max(0.196 8 mm)几乎超过允许极限,这是因为所引起的大变形表现为工件的边缘翘曲,但该区域属工件落料部位,对加工质量影响微弱,故可忽略。

图10 加工区域最大定位误差变化历程

4.1.2 支承/定位球心位置的求解 结合图2所示工装结构设计的约束,即各滑枕上支承/定位球心具有相同的x坐标,对图9所示支承/定位点布局进行微调,得到该工件支承/定位点布局,计算可得多点柔性支承/定位阵列工装的支承/定位球心空间坐标,如表1所示。

表1 支承/定位球心空间坐标 mm

4.2 实验比对分析

应用表1所示理论计算结果,进行样件的装夹定位测试,实验过程主要包括支承/定位球的标定、工件在工装系统上的夹持、工件外形定位误差的测量与分析。

4.2.1 支承/定位球标定 支承/定位球的标定是指对支承/定位球进行球心空间位置标定,标定仪器采用Leica AT901激光跟踪测量系统,标定过程分为两个阶段:①使用反射标靶对工装系统坐标系标定孔1～3进行测量,在测量软件PC-DIMS中,以标定孔1到2和标定孔1到3的连线方向分别为x轴和y轴,构建工装系统世界坐标系的xy平面,并以工装系统左下角最外侧支承/定位球心为坐标系原点,构建工装系统世界坐标系;②采用Leica AT901激光跟踪测量系统组件T-Probe,对工装各支承/定位球进行测量,并依据支承/定位球心坐标值,调整对应球心的空间坐标,以此形成工件支承面的多点包络。

4.2.2 工件的定位夹持 对应四分之一有限元分析模型,并考虑模型中对称边界的影响,选用薄壁实验工件尺寸为1 000 mm×700 mm,板厚为3 mm,材料为7075铝合金。将工件蒙在标定好的工装支承/定位球包络面上进行定位,进而开启真空吸附系统,对工件进行真空吸附夹持,如图11所示。

图11 工件的夹持定位(-0.5 MPa吸附)

4.2.3 工件定位误差的测量与分析 选用Faro Laser ScanArm多关节测量臂系统对工件定位误差进行测量,其优势在于可精确扫描黑色和高反光材质工件外形,测量精度可达0.01 mm。测量实验中,去除工件表面油污,并使用显像剂将其喷涂均匀,进而通过探头发出激光束,照射到工件表面上,采集工件表面离散点,再通过大量点云数据获取被测物的详细参数,如图12所示。

图12 工件定位误差的测量环境

将工件定位后表面实测点云数据与理论计算数据同时导入Imageware软件,以两组点云中支承/定位点为基准,对上述两组点云进行对准,进而对工件外形实测点云进行3D反求,并依据理论数据点相对位置关系对工件3D反求模型进行分割,以此实现分割后的工件表面数据点的实测拟合值与ANSYS计算结果数据进行比对。图13显示了表1所列支承/定位点布局下工件表面数据点实测值与理论计算值的比对,可见变化趋势基本一致。表2显示了工件各加工区域的最大定位误差的偏差。

图13 工件定位误差(z向)实测拟合值与理论计算值全局对比

加工区域最大定位误差/mm理论实测偏差/mm10.19680.24900.050420.17010.21300.042930.17410.14100.033140.11110.08700.0241

为了进一步观察工件定位误差的变化趋势及实测值与其理论值的偏差,分别沿图13所示x为40、270、490、660、930 mm和y为40、210、510、660 mm的方向对工件定位误差变化规律进行观察,可发现工件定位误差的变化趋势主要表现为:靠近对称边界附近的区域受对称边界条件的影响较小,但相对于工件其他位置,该处变形更大,主要原因在于实验用工件只模拟了其理论模型的四分之一部分,无法构造理论计算中的对称边界,因此与理论计算结果相比较,实物工件在靠近对称边界附近的区域缺少了理论模型中对称部分的牵拉,因此表现为较大翘曲变形,如图14、15所示。

此外,工件外侧边缘区域和非加工区域具有较大变形量,如图16、17所示,但相对加工区域处的定位误差而言,其对加工质量的影响并不显著,该布局结果也正体现了本文所提布局方法重点防护加工区域定位误差的特性。

图14 工件定位误差(z向)实测拟合值与理论计算值偏差:y=660 mm

图15 工件定位误差(z向)实测拟合值与理论计算值偏差:x=930 mm

图16 工件定位误差(z向)实测拟合值与理论计算值偏差:y=40 mm

图17 工件定位误差(z向)实测拟合值与理论计算值偏差:x=40 mm

5 结 论

本文紧密结合大型薄壁件加工过程中多点支承/定位这一基础理论问题,提出了一种跟随加工区域布置定位点的“X-2-1”定位原理与定位方法。同时,以常见的大型薄壁件的多点支承/定位为案例,展示了跟随加工区域布置支承/定位点的实现流程,对比了定位后工件外形的理论计算与实测值,结果表明对应支承/定位点布局下工件定位误差的变化趋势基本一致,且20个支承/定位点资源约束下,相应实验件最大定位误差小于0.2 mm,满足工程需求,且远远优于传统均布支承/定位点在相同实验条件下实验件0.8 mm的最大定位误差[10],进一步验证了有限支承/定位资源约束下跟随加工区域布置定位点的定位方法的正确性与合理性。

本文所提跟随加工区域布置支承/定位点的定位方法有利于设计人员在保障工件加工过程中夹持可靠的前提下,基于有限支承/定位资源对工件不同区域的定位误差实施有针对性的重点防控,并为控制工件加工变形、提高工艺系统刚度为目标的支承/定位点布局全局优化提供了可靠的优化初值。

[1] CAI W, HU S J, YUAN J. Deformable sheet metal fixturing: principles, algorithms, and simulations [J]. Journal of Manufacturing Science and Engineering, 1996, 118(3): 318-324.

[2] 胡福文, 李东升, 李小强, 等. 面向飞机蒙皮柔性夹持数控切边的定位仿真系统及应用 [J]. 计算机集成制造系统, 2012, 18(5): 993-998. HU Fuwen, LI Dongsheng, LI Xiaoqiang, et al. Locating simulation for aircraft skins NC trimming based on flexible holding fixture [J]. Computer Integrated Manufacturing Systems, 2012, 18(5): 993-998.

[3] 胡福文, 李东升, 李小强, 等. 蒙皮柔性夹持数控切边的工艺设计方法 [J]. 北京航空航天大学学报, 2012, 38(5): 675-680. HU Fuwen, LI Dongsheng, LI Xiaoqiang, et al. Process planning of aircraft skins NC trimming based on reconfigurable fixture [J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(5): 675-680.

[4] KING L S, HUTTER I. Theoretical approach for generating optimal fixturing locations for prismatic workparts in automated assembly [J]. Journal of Manufacturing Systems, 1993, 12(5): 409-416.

[5] DEMETER E C. Min-max load model for optimizing machine fixture performance [J]. Journal of Engineering for Industry, 1995, 117(2): 183-186.

[6] MENASSA R J, DEVRIES W R. Optimization methods applied to selecting support positions in fixture design [J]. Journal of Engineering for Industry, 1991, 113(4): 412-418.

[7] PONG P C, BARTON R R, COHEN P H. Optimum fixture design [C]∥Proceedings of the 2nd Industrial Engineering Research Conference. Los Angeles, CA, USA: IIE, 1993: 6-10.

[8] DEMETER E C. Fast support layout optimization [J]. International Journal of Machine Tools and Manufacture, 1998, 38(10/11): 1221-1239.

[9] 刘春青, 洪军, 王少锋, 等. 飞机薄壁件多点柔性定位变形控制寻优算法 [J]. 上海交通大学学报, 2013, 47(8): 1191-1197. LIU Chunqing, HONG Jun, WANG Shaofeng, et al. Searching optimization algorithm for deformation control of aircraft thin-walled parts in multi-point flexible tooling system [J]. Journal of Shanghai Jiaotong University, 2013, 47(8): 1191-1197.

[本刊相关文献链接]

吴继琸,朱刚贤,陆斌,等.自愈合效应对光内送粉激光变斑熔覆成形薄壁件的影响.2016,50(1):145-150.[doi:10.7652/xjtuxb201601022]

周强,刘志刚,洪军,等.卡尔曼滤波在精密机床装配过程误差状态估计中的应用.2015,49(12):97-103.[doi:10.7652/xjtuxb201512016]

侯明明,吴九汇,姜宁.旋转封闭薄壁球壳辐射噪声的多极展开方法.2014,48(7):102-108.[doi:10.7652/xjtuxb201407 018]

黄泽华,李建勇,樊文刚,等.复杂曲面薄壁叶片点铣加工弹性变形预测.2012,46(5):67-72.[doi:10.7652/xjtuxb2012 05012]

徐海洋,宋国兵,樊占峰,等.行波波头的参数识别方法在高压直流输电系统中的应用.2016,50(2):85-90.[doi:10.7652/xjtuxb201602015]

王新孟,杨军,梅雪松,等.精密坐标镗床进给系统热误差分析与预测.2015,49(10):22-28.[doi:10.7652/xjtuxb201510 004]

郝双晖,王磊,宋宝玉,等.交流伺服系统永磁同步电机电流及位置二级状态观测器设计.2015,49(5):100-107.[doi:10.7652/xjtuxb201505016]

吴杰,冯祖仁,刘恒,等.水下目标多元声传感阵列网络定位方法.2015,49(4):40-45.[doi:10.7652/xjtuxb201504007]

董恩清,刘伟,宋洋.采用三角形节点块处理无线传感器网络节点定位中节点翻转歧义的迭代方法.2015,49(4):84-90.[doi:10.7652/xjtuxb201504014]

王云龙,吴瑛.联合时延与多普勒频率的直接定位改进算法.2015,49(4):123-129.[doi:10.7652/xjtuxb201504020]

(编辑 赵炜 杜秀杰)

Initial Distribution Optimization for Multi-Point Location of Large Thin-Walled Components

WANG Shaofeng1,2,HONG Jun2,WANG Jianguo1,LI Baotong2,YANG Zhaohui3

(1. School of Mechanical Engineering, Inner Mongolia University of Science and Technology, Baotou, Inner Mongolia 014010, China; 2. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 3. School of Aeronautics, Northwestern Polytechnical University, Xi’an 710072, China)

To restrain the dynamic change of effective locators in the manufacturing process of large thin-walled components, a new “X-2-1” locating method is proposed to distribute the location/support points following machining region, with the goal to meet the requirements for the clamping force, positioning accuracy and maximum support capacity. This method can ensure reliable clamping in the machining process of workpieces, and control positioning error in different machining regions. Simulation and experiment show that the maximum positioning error is 0.2 mm, much better than that obtained when twenty location/support points are distributed evenly over the whole support area of a workpiece. The improvement suppresses the perturbations of clamping deformation to machining quality. Furthermore, the optimization result of initial distribution of location/support points provides a foundation for a further global optimization of multi-point location distribution of large thin-walled components so as to increase process system’s stiffness, decrease machining distortion, and improve machining quality.

thin-walled component; multi-point location; initial distribution

10.7652/xjtuxb201605006

2015-10-27。 作者简介:王少锋(1980—),男,讲师。 基金项目:国家自然科学基金青年基金资助项目(51405377)。

时间:2016-03-04

http:∥www.cnki.net/kcms/detail/61.1069.T.20160304.1649.002.html

TH161

A

0253-987X(2016)05-0038-07