轴向拉紧的圆弧端齿轴段扭转特性研究
2016-12-24夏凯孙岩桦洪德江赵世全
夏凯,孙岩桦,洪德江,赵世全
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;3.东方汽轮机有限公司,618000,四川德阳)
轴向拉紧的圆弧端齿轴段扭转特性研究
夏凯1,2,孙岩桦1,2,洪德江2,赵世全3
(1.西安交通大学机械工程学院,710049,西安;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;3.东方汽轮机有限公司,618000,四川德阳)
为了研究轴向拉紧的圆弧端齿轴段的扭转特性,提出了圆弧端齿轴段传扭特性的分段线性模型,给出了分段线性转折点处扭矩的估计值,同时建立了轴向预紧圆弧端齿轴段三维有限元模型,采用数值计算对理论分析进行了验证。此外,通过数值计算求得圆弧端齿轴段的双线性扭转刚度,并进一步研究了预应力、摩擦系数等参数对圆弧端齿扭转特性的影响。研究结果表明:圆弧端齿结构具有典型的软弹簧双线性扭转特性,预应力对圆弧端齿的传扭特性有影响且存在预紧饱和现象;预紧饱和后,圆弧端齿双线性刚度基本不受预应力的影响,分段线性转折点扭矩则与预应力成正比;摩擦系数对圆弧端齿双线性刚度的起始段刚度基本无影响,仅对线性特性的第二段刚度有影响,扭转刚度随摩擦系数的增大而增大。研究结果对工程应用中端齿连接的设计及重型燃气轮机转子动力学分析具有参考价值。
重型燃气轮机;转子;圆弧端齿;扭矩;刚度
圆弧端齿传扭能力强,结构强度高,且具有良好的自对中性能,大量应用于航空发动机转子和大功率工业燃气轮机转子上。对于重型燃气轮机,其透平转子一般采用带有端齿的多个轮盘在轴向用拉杆拉紧的结构,与整锻式转子或焊接式整体转子相比,圆弧端齿的存在在一定程度上削弱了整个转子的刚度。为了能更精确地分析此类转子的动力学特性,需要深入研究圆弧端齿轴段的传扭能力及扭转刚度等特性。
目前,关于圆弧端齿的研究文献在齿面应力方面居多,端齿刚度方面的研究很少,而直接对端齿扭转刚度的研究更是缺乏。Yuan等采用GW模型[1]研究了拉杆预紧下的圆弧端齿接触面的等效抗弯刚度与预紧力和接触面表面粗糙度的关系[2]。然而,GW模型、MB模型[3]等粗糙接触面刚度解析模型仅适用于接触面压力不大的情况,在解决复杂形体接触及大载荷作用下的接触问题存在一定的局限性[4-5]。尹泽勇等提出了端齿梁单元模型,采用有限元法计算了端齿梁单元弯曲刚度矩阵,分析了端齿轴段弯曲刚度与变轴力的关系,研究了端齿轴段弯曲刚度对航空发动机转子动力特性的影响,深化了对端齿接触问题的认识,为端齿轴段扭转刚度的研究提供了思路[6-8]。Liu等建立了平面端齿段的三维有限元模型,静态分析得到了端齿段的弯曲刚度,通过等效弹性模量计入端齿段刚度,研究了某实验拉杆转子的动力特性[9]。李浦等基于三维有限元非线性接触算法计算了周向拉杆预紧下轮盘平面端齿轴段的扭转刚度,研究发现,当作用扭矩较大时,端齿轴段扭转刚度存在急剧减小的现象[10],但是文中没有对此给予充分的解释,也没有考虑摩擦系数对扭转刚度的作用。
与端齿轴段弯曲刚度不同,在研究端齿轴段扭转刚度、传扭能力等特性时,需要综合考虑端齿接触面摩擦系数、预紧力等因素的影响。本文针对某重型燃气轮机透平转子轴向预紧圆弧端齿轴段的结构特点,通过理论分析提出了端齿轴段传扭特性的分段线性模型,并通过三维有限元数值计算进行了验证。此外,通过数值计算求得端齿轴段分段线性的扭转刚度,并分析预紧力、摩擦系数等对扭转特性的影响。本文的研究希望能对工程应用中端齿连接的设计及重型燃气轮机转子动力学分析提供参考。
1 圆弧端齿配合的扭转特性
1.1 圆弧端齿结构
图1为某重型燃气轮机透平转子半剖面示意图。该透平转子由多级轮盘通过数根周向均布拉杆拉紧装配而成,轮盘之间通过圆弧端齿啮合定位并传递扭矩。图2为轮盘间的圆弧端齿配合示意,图中凹齿的两侧齿面均为凹面,凸齿的两侧齿面均为凸面,凹齿与凸齿相互啮合起到定心传扭的作用。圆弧端齿主要齿形参数包括圆弧端齿内径Di、外径Do、齿宽B、齿数Z、压力角θ、齿顶高ha、齿根高hb、全齿高hf、齿顶倒角角度λc、齿顶倒角高度hc、齿根过渡圆角半径Rg和山形底高hg等,圆弧端齿轴段的长度为Lb。
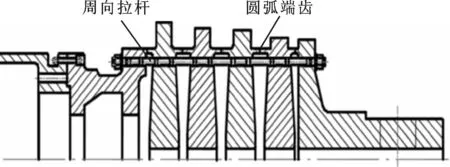
图1 某重型燃气轮机透平转子半剖面示意图
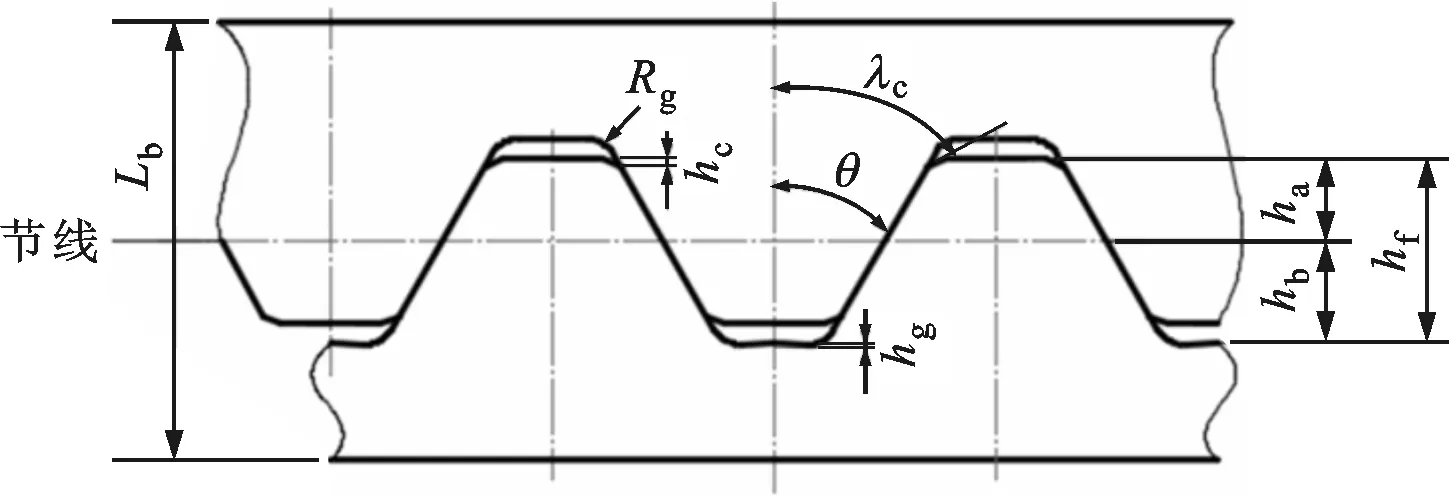
图2 圆弧端齿结构参数及啮合关系
1.2 圆弧端齿配合的受力分析及临界载荷
对于轴向拉紧的圆弧端齿配合,取其中的一对齿进行分析,在扭转时其中的凹齿受力情况如图3所示。凹齿轴段轴向预紧力为Fa,切向力为Fτ,Fτ=2T/Dm,其中T为扭矩,Dm为节圆直径,Dm=(Do+Di)/2。凹齿齿面有法向力Fn1、Fn2和摩擦力Ft1、Ft2。在受力平衡状态下有
Fa=Fn1sinθ+Fn2sinθ+Ft1cosθ+Ft2cosθ
(1)
Fτ=-Fn1cosθ+Fn2cosθ+Ft1sinθ-Ft2sinθ
(2)
其中两个齿面上的法向力Fn1、Fn2满足下面的单边接触条件
(3)
摩擦力Ft1、Ft2是静摩擦力,其方向与两个界面的相对运动趋势有关,在扭转过程中满足
(4)
式中:μ为摩擦系数。
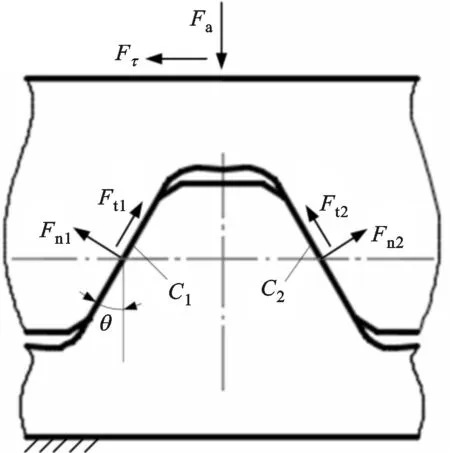
图3 圆弧端齿凹齿受力图
在扭转过程中,随着扭矩T的增大,齿面C1上的压力减小而齿面C2上的压力增大,当Fn1=0时,齿面C1分离。由于齿面C2上有摩擦力,可以提供额外的力来平衡切向力,使得端齿连接还能承受更大的周向载荷而不分离。但是,随着Fτ进一步增大,齿面C2上的摩擦力达到最大静摩擦力后会发生滑动,此时存在临界载荷Fτmax满足Fn1=0,Ft1=0,Ft2=-μFn2,将其带入式(1)和式(2)可得
(5)
式(5)给出了一个受轴向预紧力Fa作用的端齿连接所能承受的最大周向载荷,它只与端齿的压力角、齿面的摩擦系数和轴向预紧力有关。如果忽略齿面上的摩擦力,即当μ=0时,端齿连接所能承受的最大周向载荷满足
(6)
当Fτ>Fτmax时,端齿接触面发生滑动,切向刚度变为0,端齿轴段扭转刚度趋于0。Fτmax对应的临界扭矩为
(7)
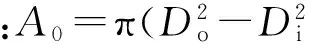
(8)
上述分析表明,在端齿轴段的扭转过程中,其中一个配合齿面会出现分离。在齿面分离前,由于两边的齿面都是配合的,所以齿的切向变形会受到两边齿面的约束,相应的端齿轴段扭转刚度比较大;当一个齿面出现分离时,这个接触界面成为自由界面,只有另一边的齿面受摩擦力而产生约束,相应的端齿轴段扭转刚度减小。因此,端齿连接的扭转特性会由于一个配合齿面的分离而发生突变。如果假定在齿面分离前后轴段的扭转变形都是线性的,那么整个扭转特性必然表现为典型的分段线性特性,如图4所示。
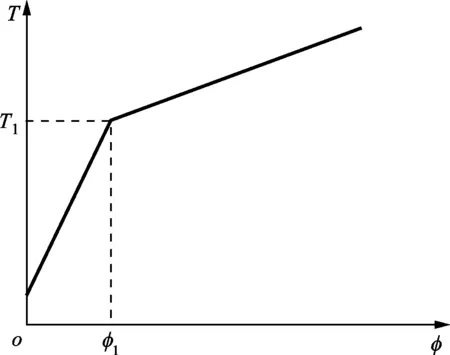
图4 圆弧端齿扭转分段线性特性示意图
对于一个轴向拉紧的端齿配合,在没有扭矩作用时,每个齿两个齿面上的摩擦力方向必然与该齿受到的轴向压紧力的方向相反,见图3。以凹齿为例,当齿面C1上的摩擦力减小到0时,该齿面脱离接触。继续增大切向力,仍然接触的齿面C2趋向于沿齿面滑动,该齿面上的摩擦力方向将发生反转。假设齿面C1脱离接触时,齿面C2上的摩擦力正好为0,该情况相当于两个齿面上的摩擦系数为0时给端齿连接施加最大的周向载荷。因此,图4中分段线性特性的转折点对应的扭矩就是式(8)确定的无摩擦时的端齿连接所能承受的最大扭矩。
需要说明的是,上述的分析不考虑端齿的局部滑动和分离,假定在扭转过程中齿面的滑动和脱离都是整体的,但这与实际情况不同。实际的端齿各处受力情况并不完全一致,接触状态随切向载荷的变化不完全同步,齿面的脱离也一定是从局部开始的。事实上,本文目的恰恰是要研究在这个扭转过程中端齿本身的扭转刚度。上述的分析虽然简单,但仍然可以给出这样一个端齿配合在扭转过程中的两个关键点的载荷估计,这对端齿传扭能力的设计非常重要。
1.3 扭转刚度修正系数
为了比较端齿连接和连续轴段扭转特性的差别,定义如下的刚度修正系数
(9)
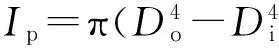
(10)
2 圆弧端齿轴段扭转特性有限元分析
为了验证前述理论分析得到的端齿轴段分段线性的传扭特性,本节将利用有限元分析软件ANSYS进行三维接触分析,并且计算端齿轴段的扭转刚度。
圆弧端齿轴段的配合具有周期循环对称性,为了简化计算,可以取一对齿的部分模型进行分析,最终建立的有限元模型如图5所示,各参数见表1。实体建模采用Solid 186单元,该单元为高阶3D20节点实体单元,采用了二次插值函数,对不规则形状具有良好的精度。凹齿与凸齿啮合采用面-面接触单元进行建模,包括接触单元Conta 174和目标单元Targe 170。图5中前端面施加预应力,以模拟拉杆预紧力的作用;前端面外圆弧线上节点施加切向力,用以模拟施加在轴段的扭矩的作用;后端面采用固定约束。为了减小施加切向载荷引起的应力集中对弧形端齿轴段扭转变形的影响,建模轴段应尽可能长,经过验算,建模轴段L0=200 mm或者更长时,该影响可以忽略。
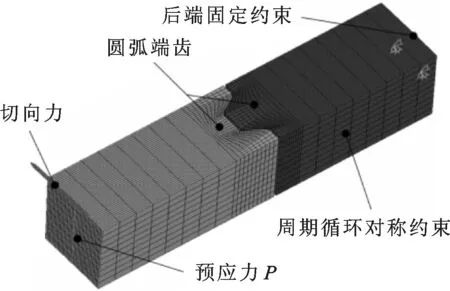
图5 端齿轴段扭转刚度计算有限元模型及边界条件
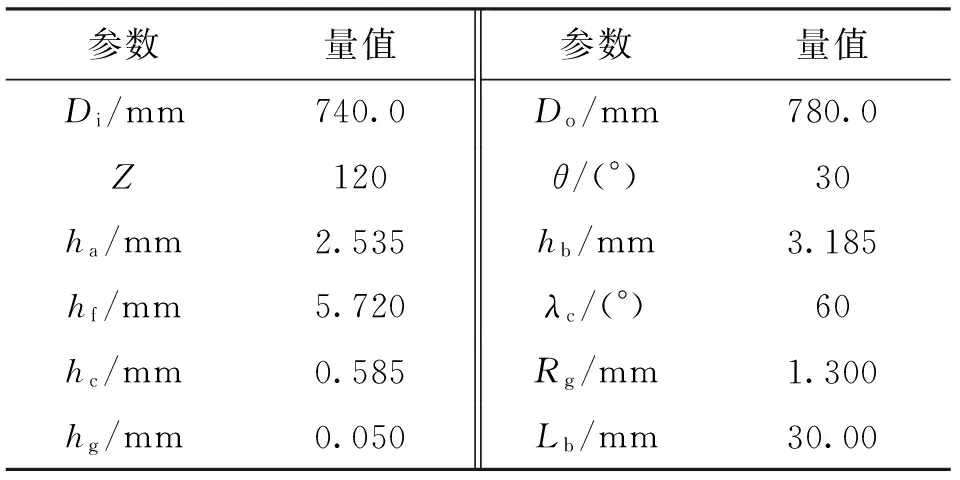
参数量值参数量值Di/mm740.0Do/mm780.0Z120θ/(°)30ha/mm2.535hb/mm3.185hf/mm5.720λc/(°)60hc/mm0.585Rg/mm1.300hg/mm0.050Lb/mm30.00
此外,假设作用在端齿轴段两端面的预紧力在外部扭矩的变化过程中保持不变。在工程上,不同截面尺寸的连接轴段预紧力相差很大,而相应的预应力变化范围较小,因此本文采用预应力作为研究变量,使研究结果更具适用性。
预应力P=40 MPa时端齿轴段的扭转变形关系如图6所示。μ=0.2时有限元临界扭矩Tlim=2.26 MN·m,当施加扭矩T>Tlim,a时齿面C2发生整体滑动,采用式(7)估算的临界扭矩Tlim,a=2.15 MN·m,临界扭矩估算值Tlim,a与有限元计算值Tlim非常接近,相对误差为4.87%。μ=0时有限元临界扭矩Tlim=1.25 MN·m,采用式(8)估算的临界扭矩Tlim,a=1.26 MN·m,临界扭矩估算值Tlim,a与有限元计算值Tlim的相对误差只有0.8%,两者吻合非常好。这说明前述的理论分析可以给出端齿承载临界扭矩的较准确估计,用于在设计时进行端齿结构传扭能力的计算。
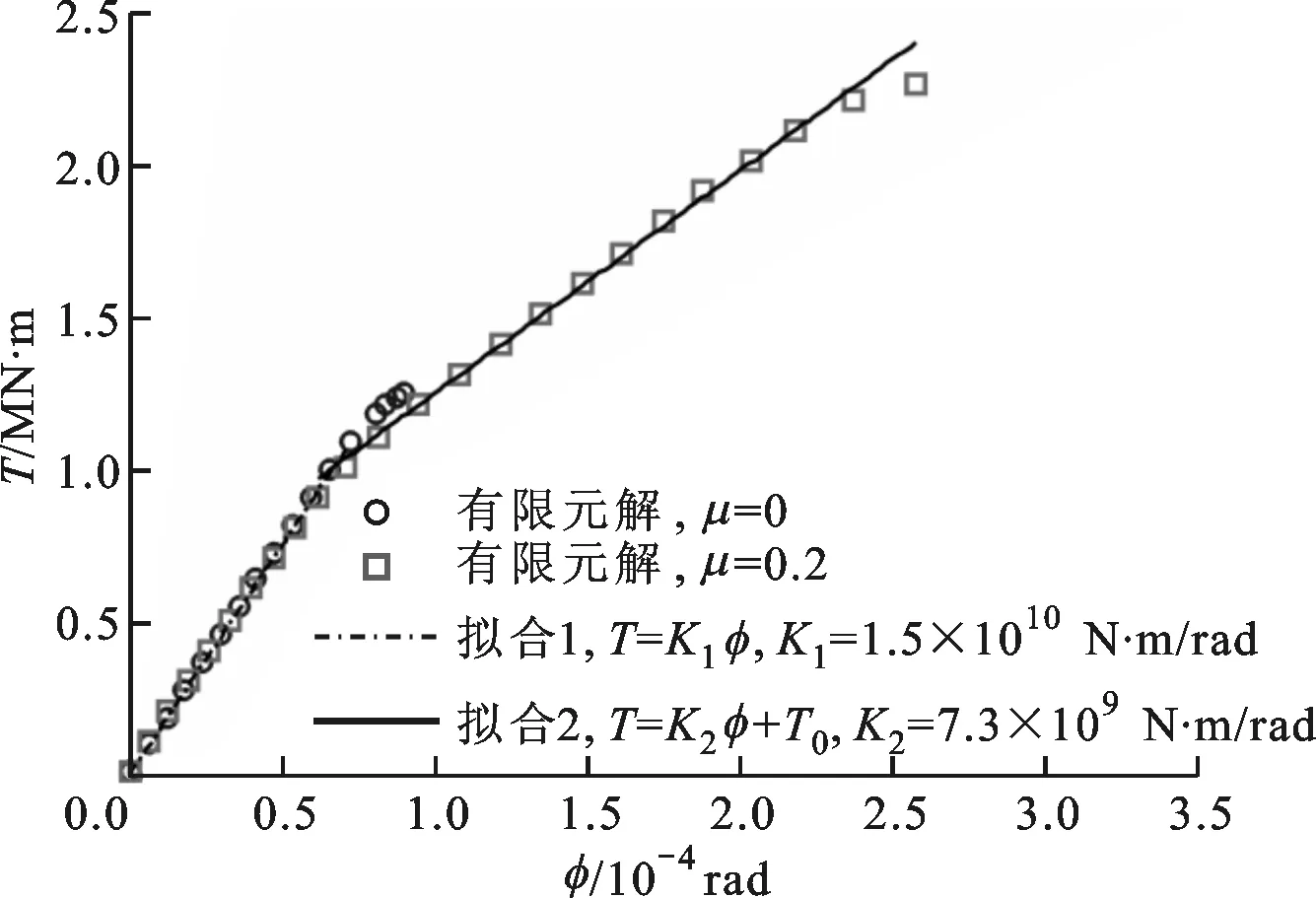
图6 端齿轴段扭转变形曲线
从图6还可以看出,与理论分析一致,端齿轴段的扭转变形呈现明显的分段线性特性。图中,拟合1和2的交点是(T1,φ1),T1=1.01 MN·m。可以认为,该点是齿面C1的近似分离点。有限元计算得到齿面C1完全分离时的临界扭矩Tlim=1.16 MN·m,比T1稍大。C1分离时扭矩的估算值Tlim,a=1.26 MN·m,估算值与有限元计算值比较接近,两者相对误差为8.6%。因此,式(8)给出了端齿齿面C1分离点扭矩的较好估计。
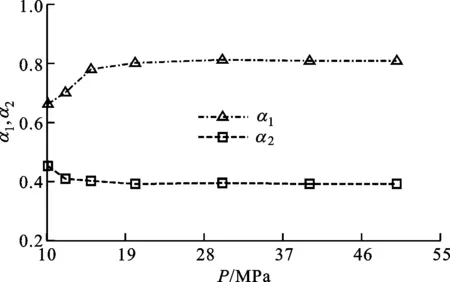
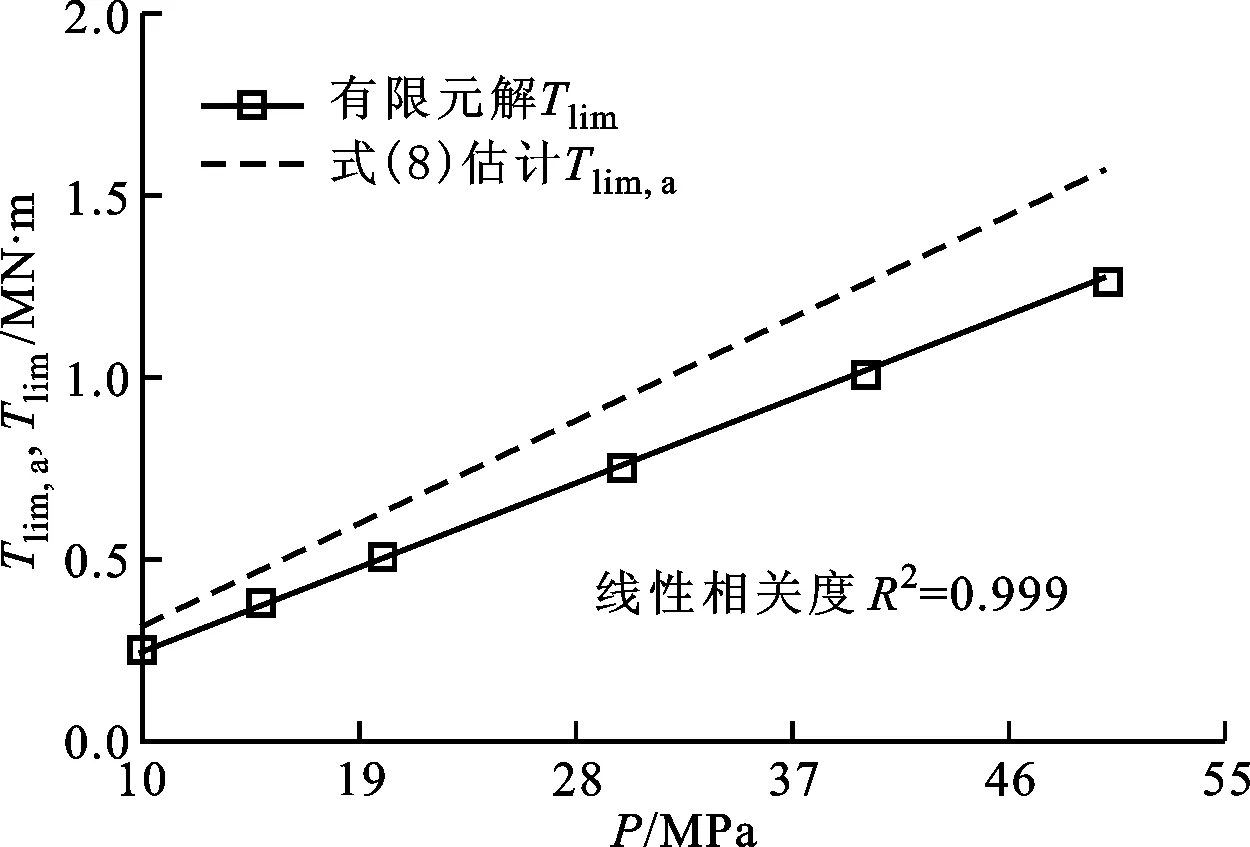
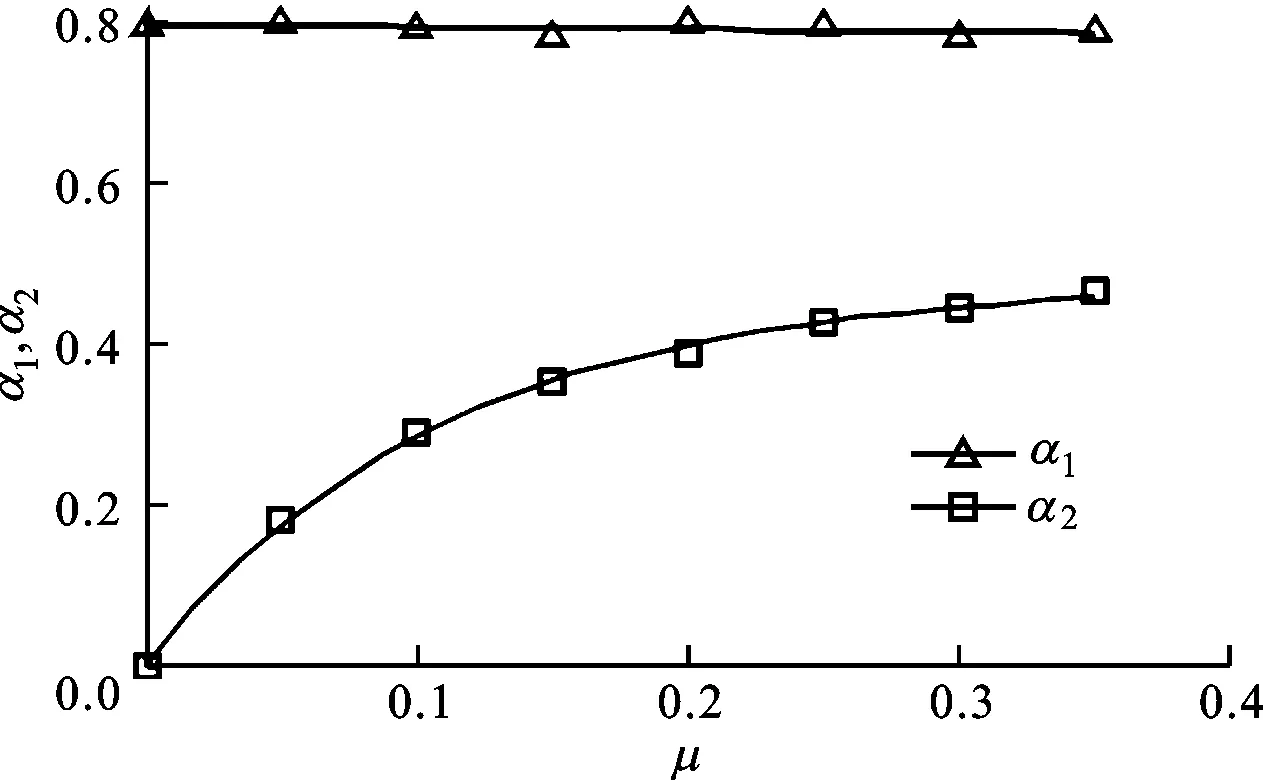
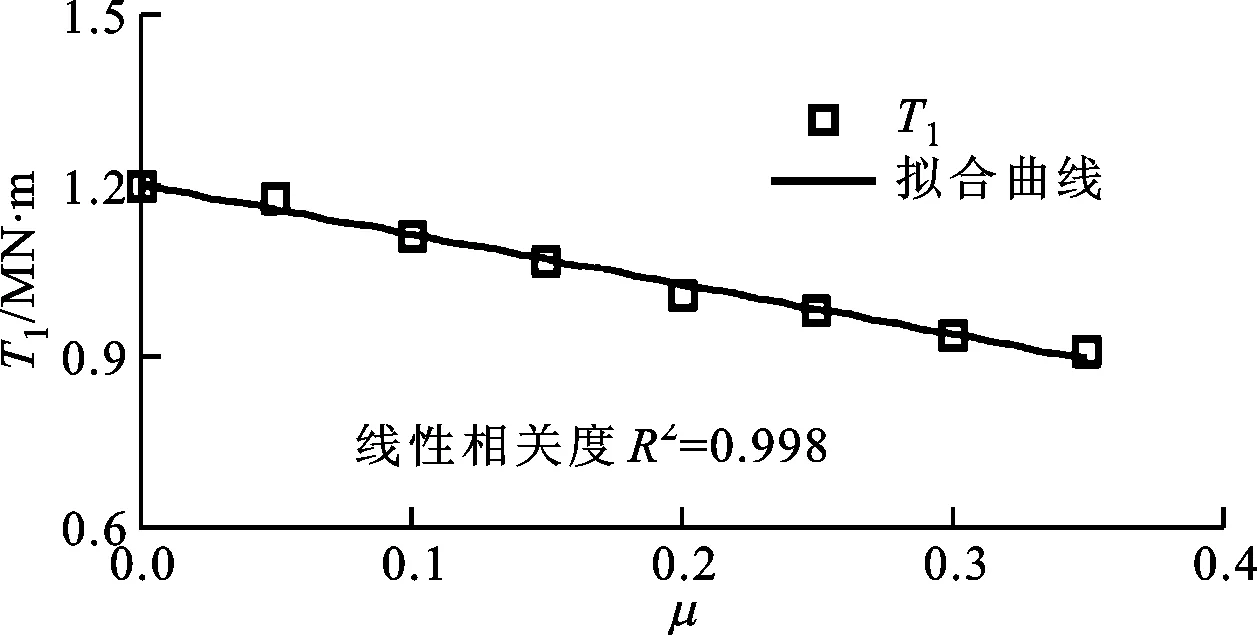
此外,端齿轴段刚度转折点发生在齿面C1完全分离之前,即T1 端齿轴段扭转变形的双线性特性可以表示为 (11) (12) 式中:K1、K2为圆弧端齿轴段双线性刚度;T0=(K1-K2)φ1。因此,圆弧端齿轴段扭转刚度修正系数α1=K1/K0,α2=K2/K0。 图7 端齿齿面的接触状态 3.1 预应力的影响 取圆弧端齿接触面摩擦系数μ=0.2,端齿几何参数见表1,端齿轴段扭转刚度修正系数和分段线性转折点扭矩随预应力的变化如图8所示。 (a)扭转刚度修正系数 (b)分段线性转折点扭矩图8 预应力对端齿轴段扭转特性的影响 由图8a可以看出:预应力较小(P<20 MPa)时,端齿轴段预紧不足,扭转刚度修正系数α1随着预应力P的增大而增大,α2随着预应力P的增大而减小;预应力较大(P≥20 MPa)时,端齿轴段达到预紧饱和状态,随着预应力P的增大α1、α2基本不变,分别维持在0.81和0.40附近,前后变化均不超过1%。 由图8b可以看出,有限元法计算的分段线性转折点扭矩随预应力的增大而线性增大,这与理论分析一致。由线性回归分析结果可知,分段线性转折点扭矩与预应力近似成正比(线性相关度R2=0.999)关系。比较式(8)与有限元数据的线性回归方程可知,分段线性转折点扭矩估算值与有限元值的相对误差为23.5%。 3.2 摩擦系数的影响 扭转刚度修正系数及分段线性转折点扭矩随摩擦系数的变化如图9所示。由图9a中拟合数据可以看出:扭转刚度修正系数α1维持在0.81附近,基本不受摩擦系数的影响。这是因为在齿面C1脱离前,凹齿与凸齿配合紧密,在弹性小变形范围内端齿扭转刚度保持不变,与理论分析吻合;扭转刚度修正系数α2随摩擦系数的增大而增大,最后趋于平稳,在0~0.35的摩擦系数范围内,刚度修正系数α2位于0~0.47之间。 (a)扭转刚度修正系数 (b)分段线性转折点扭矩图9 摩擦系数对端齿轴段扭转特性的影响 由图9b线性回归分析结果可知,分段线性转折点扭矩T1与摩擦系数近似线性相关(相关度为R2=0.988),摩擦系数减小0.1,相应的分段线性转折点扭矩减小87.21 kN·m,占无摩擦时转折点扭矩的7.26%,可见摩擦系数虽然有影响,但影响不太大。 本文针对某重型燃气轮机透平转子圆弧端齿轴段的结构特点,建立了圆弧端齿理论分析模型,研究了端齿轴段分段线性的传扭特性,并通过三维有限元数值计算进行了验证。 (1)圆弧端齿轴段扭转特性是典型的分段线性特性,可以用软弹簧特性的双线性模型来近似,而双线性特性的转折点临界扭矩大小可以通过无摩擦的端齿配合最大扭矩来估算。 (2)圆弧端齿轴段扭转特性与预紧力有关,且出现预紧饱和现象。端齿轴段处于预紧饱和状态时,圆弧端齿双线性刚度保持不变,此时分段线性转折点扭矩则与预应力成正比。 (3)摩擦系数对起始段圆弧端齿双线性刚度基本没有影响,只对线性特性的第二段刚度有影响,增大摩擦系数可以提高圆弧端齿轴段在此扭矩范围内的扭转刚度。此外,摩擦系数对分段线性转折点扭矩的影响不大。 上述的双线性刚度特性将对转子的扭转振动产生影响,可能导致工作中的转子产生一些非线性振动现象,这需要进一步深入研究。 [1] GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces [J]. Proceedings of the Royal society of London: Series A, 1966, 295: 300-319. [2] YUAN Shuxia, ZHANG Youyun, ZHU Yongsheng, et al. Study on the equivalent stiffness of heavy-duty gas turbines composite rotor with curvic couplings and spindle tie-bolts [C]∥Proceedings of ASME Power Conference. New York, USA: ASME, 2011: 1-10. [3] MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces [J]. ASME Journal of Tribology, 1991, 113(1): 1-11. [4] 李辉光, 刘恒, 虞烈. 粗糙机械结合面的接触刚度研究 [J]. 西安交通大学学报, 2011, 45(6): 69-74. LI Huiguang, LIU Heng, YU Lie. Contacts tiffness of rough mechanical joint surface [J]. Journal of Xi’an Jiaotong University, 2011, 45(6): 69-74. [5] 饶柱石, 夏松波, 汪光明. 粗糙平面接触接触刚度的研究 [J]. 机械强度, 1994, 12(2): 72-76. RAO Zhushi, XIA Songbo, WANG Guangming. A study of contact stiffness of flat rough surface [J]. Journal of Mechanical Strength, 1994, 12(2): 72-76. [6] 尹泽勇, 欧圆霞, 李彦, 等. 端齿轴段刚度及其对转子动力学特性的影响 [J]. 振动工程学报, 1993, 6(1): 63-67. YIN Zeyong, OU Yuanxia, LI Yan, et al. Stiffness of a shaft section with curvic couplings and its effect on dynamic characteristic of a rotor [J]. Journal of Vibration Engineering, 1993, 6(1): 63-67. [7] 尹泽勇, 欧园霞, 胡柏安, 等. 端齿连接及变轴力的影响 [J]. 航空动力学报, 1994, 9(2): 129-132. YIN Zeyong, OU Yuanxia, HU Bo’an, et al. Rotor with curvic couplings and the influence of variable axial force [J]. Journal of Aerospace Power, 1994, 9(2): 129-132. [8] 尹泽勇, 胡柏安, 吴建国, 等. 端齿连接转子轴向预紧力的确定 [J]. 航空动力学报, 1996, 9(2): 355-357. YIN Zeyong, HU Bo’an, WU Jianguo, et al. Determination of axial preloads of rotor with curvic couplings [J]. Journal of Aerospace Power, 1996, 9(2): 355-357. [9] LIU Xin, YUAN Qi, LIU Yang, et al. Analysis of the stiffness of Hirth couplings in rod-fastened rotors based on experimental model parameter identification [C]∥Proceedings of ASME Turbo Expo. New York, USA: ASME, 2014: 1-10. [10]李浦, 袁奇, 高进, 等. 轮盘端面齿连接的周向拉杆转子刚度研究 [J]. 航空动力学报, 2013, 28(7): 1618-1623. LI Pu, YUAN Qi, GAO Jin, et al. Investigation on stiffness of circumferential distributed tie-rod rotor with curvic couplings of trochal disk [J]. Journal of Aerospace Power, 2013, 28(7): 1618-1623. [本刊相关文献链接] 刘雨薇,张卫正,叶福浩.单个微凸体接触过程中的闪点温度研究.2016,50(3):90-93.[doi:10.7652/xjtuxb201603014] 刘香浪,张英杰,李云龙,等.面向低碳制造的切削液供给系统优化研究.2016,50(2):91-97.[doi:10.7652/xjtuxb201602 016] 刘雅琳,上官博,徐自力.干摩擦阻尼对失谐叶盘系统受迫振动的影响.2016,50(2):111-117.[doi:10.7652/xjtuxb201602 019] 蒲伟,王家序,杨荣松,等.重载下准双曲面齿轮传动界面润滑机理分析.2015,49(11):55-61.[doi:10.7652/xjtuxb2015 11010] (编辑 苗凌) Torsional Characteristics of Axial Fastened Shaft Section with Curvic Couplings XIA Kai1,2,SUN Yanhua1,2,HONG Dejiang2,ZHAO Shiquan3 (1. School of Mechanical Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China; 3. Dongfang Turbine Co., Ltd., Deyang, Sichuan 618000, China) To reveal the torsional characteristics of axial fastened shaft with curvic couplings, a piecewise linear torsional deformation model for the shaft section with curvic couplings is proposed, and the torque at the turning point is estimated. Additionally, a 3-D finite element model for the axial pre-tightened shaft section with curvic couplings is created to validate the theoretical analysis. The bilinear torsional stiffness is obtained by numerical analysis, and the effects of prestress and friction coefficient on torsional behaviors are discussed. The results show that the shaft section with curvic couplings has typical bilinear torsional characteristic of soft spring, the prestress affects torsional behaviors, and there exists a preload saturation. In the saturated preload state, the bilinear torsional stiffness has almost no relation with prestress, and the torque at the turning point gets proportional to the prestress. Moreover, the friction coefficient exerts almost no effect on the primary bilinear torsional stiffness, but heightens the secondary one. heavy duty gas turbine; rotor; curvic couplings; torque; stiffness 10.7652/xjtuxb201605008 2015-12-12。 作者简介:夏凯(1989—),男,博士生;孙岩桦(通信作者),男,副教授。 基金项目:国家“973计划”资助项目(2013CB035705);国家自然科学基金资助项目(51275386)。 时间:2016-03-01 http:∥www.cnki.net/kcms/detail/61.1069.T.20160301.1017.012.html TH113;TH117 A 0253-987X(2016)05-0051-06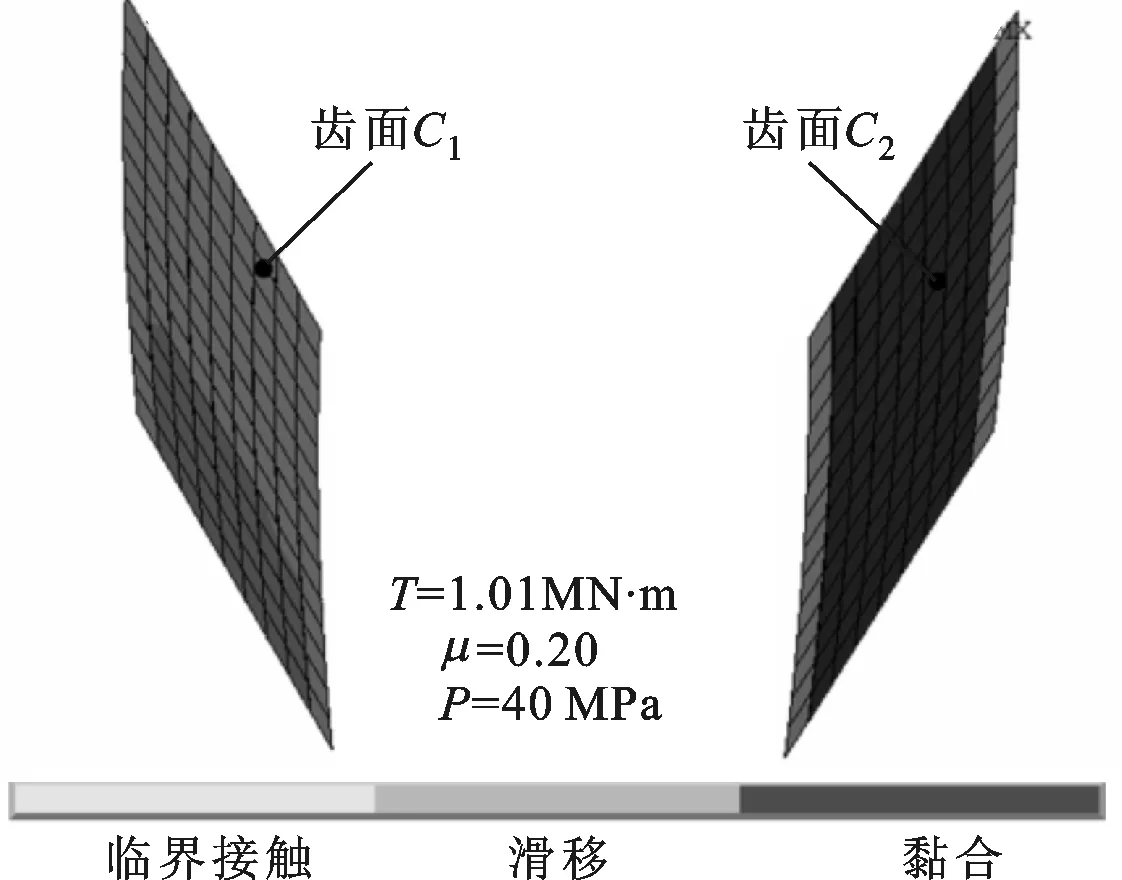
3 圆弧端齿轴段扭转特性影响因素
4 结 论
