移动互联网金融下签名认证静态特征提取技术

何殿源,冯 筠,杨晓萌

(西北大学 信息科学与技术学院,陕西 西安 710127)



·信息科学·

移动互联网金融下签名认证静态特征提取技术

何殿源,冯 筠,杨晓萌

(西北大学 信息科学与技术学院,陕西 西安 710127)

在签名图像预处理研究的基础上,提出了通过提取图像形状特征、不变距特征以及基于Gabor滤波纹理方向特征而得到签名图像静态特征的方法,并通过基于稀疏表示的L1范数分类方法在提取的特征样本集上进行签名鉴别。实验结果表明,在相同10组样本的特征集下,稀疏分类最小残差法的平均FRR和平均FAR分别为9.25%和4.63%,明显低于经典KNN法的12.15%和8.67%,也明显低于经典SVM法的13.31%和7.26%。该文的研究成果达到了移动互联网金融业务的性能要求。

互联网金融；静态特征;提取技术;L1范数;稀疏表示

为解决基于手机的移动互联网金融平台下客户登录时遇到的“你是谁”和系统交易时“你是你”的问题,签名鉴别技术研究得到了互联网金融企业和相关科研机构的高度关注。作为基于签名鉴别技术的关键,签名特征值的提取成为了移动互联网金融下身份识别技术重点研究的课题,并取得了广泛的成果。LÜ Hairong[1]等人利用笔段特征、空间分布特征、轮廓检测等方法提取字形结构,该方法可有效区分相似字。但是，对结构特征提取不理想。Alessandro[2]等人运用统计方法、距离度量匹配准则,采用多维特征值累加的办法把噪声最小化,具有良好的鲁棒性。但是，无法很好地利用一些敏感特征。张大海[3]等人通过从签名中直接提取的和通过派生得到的3级共188个特征,利用自定义的特征重要性函数进行特征选择,将用特征函数选择的个性特征用SVM算法进行训练和验证。王珂敏[4]改进了传统的动态时间弯折算法结构,对最佳匹配路径的动态规划方法进行改进并将其应用于在线签名鉴别系统。肖春景[5]等人提出了基于小波包的特征提取方法，解决了特征提取过程不可逆的问题，并降低了特征提取的困难性。陈晓红[6]等人利用计算机技术提取和分析纸上签名的宽度、灰度和弧度等动态特征数据,研究其规律并创立了一种新型的定量化签名笔迹鉴别技术,但在基于移动设备的互联网金融应用实验中,效果并不理想。从国内外的研究现状看,对从签名样本中提取能反映个人书写风格的有效特征值的研究,目前还没有可应用的研究成果，文中给出了从通过滤波、归一化、二值和灰度化等技术进行预处理后的签名笔迹中提取体现个人书写风格的静态特征的有效方法和技术。

1 签名笔迹静态特征的分类

签名特征的分类存在很多方法,例如Samuel将签名的特征分为全局特征和局部特征两大类[7]; Blayvas等人将签名特征划分为全局、统计、几何以及拓扑特征等多种[8]。对于特征的分类更多的是从实际需求来进行考虑。对于汉字而言,可以将签名笔划的方向、字体的拉伸度、密度,倾斜度等反映个人书写习惯的信息作为有效的鉴别签名的特征信息。实验证明,形状特征、矩特征、以及纹理特征能够全面地刻画签名的静态特征[9]。

2 签名特征提取

2.1 形状特征

2.1.1 字体骨架的倾斜方向向量 中文签名基本上都是由横撇竖捺等笔划构成,因此对于同一个人的手写签名,他的书写笔划在方向上的变化基本是固定的。文中实验采用签名的二值骨架提取笔划的倾斜方向特征,该方法可以有效地反映笔划在方向上的变化。记笔划骨架上的某一点为P(x,y),定义P点3个倾斜方向的特征向量为v(d1,d2,d3),分别记为笔划正倾斜方向d1，笔划垂直倾斜方向d2,以及笔划负倾斜方向d3,如图1所示,d1,d2,d3取值为0或1。

图1 垂直、正负倾斜方向Fig.1 Vertical, positive and negative tilt

骨架方向倾斜点定义:关于骨架上的某一点P(x,y),如果P′=P(x-1,y+1)非零,那么定义P′为负方向倾斜点;如果P′=P(x,y+1)非零,那么定义P′为垂直方向倾斜点;如果P′=P(x+1,y+1)非零,则定义P′为正方向倾斜点,我们将这3类点统称为骨架倾斜点。

最终,在签名骨架上的点的3个倾斜方向上进行累计求和,得3维向量V(D1,D2,D3),其中D1=∑d1,D2=∑d2,D3=∑d3,Vf=(D1,D2,D3)=(D1/D,D2/D,D3/D),其中D=D1+D2+D3。

2.1.2 签名网孔数与连通域数 签名网孔数和连通域的个数两者都属于汉字的局部几何特征,同时具有大小、平移不变性等特点,可以有效区分视觉上不能直观鉴别的局部差异[10]。签名网孔数指的是黑色笔迹所包围的封闭空白区域个数。连通域个数指的是签名笔划中彼此连接在一起的部分区域的个数。针对同一个人的签名来说,他的局部签名网孔数与笔划的连通性大体上是保持稳定的。因此,我们可以将签名网孔数与连通域个数作为一对局部有效特征。其原理示意图分别如图2所示。

图2 签名笔迹局部特征示例Fig.2 Local features of signatures example

本文采用图像形态学算法中的漫水填充算法[11]以及二值轮廓签名提取方法来统计签名网孔数和连通域个数,该算法思路如下:在二值化签名图像中,选取任意像素作为背景种子点,进而将近邻区域所有相似点都填充上同样颜色,得到填充操作的结果一般总是某个联通的区域。最后,统计二值签名图像中没有颜色变化的区域计数,即为签名网孔数。求取连通域数之前需要对于平滑签名图像的边缘轮廓进行提取,选取背景种子点之后再次利用上述漫水填充法填充背景。实验时，多次选取种子点进行填充,在字体笔划内部某些闭合区域处得到较好处理效果,图3(a)给出了签名图像轮廓提取图,图3(b)为多次选取背景种子点填充之后的效果图。扫描图像中颜色没有变化的区域计数,得到签名的连通域数。

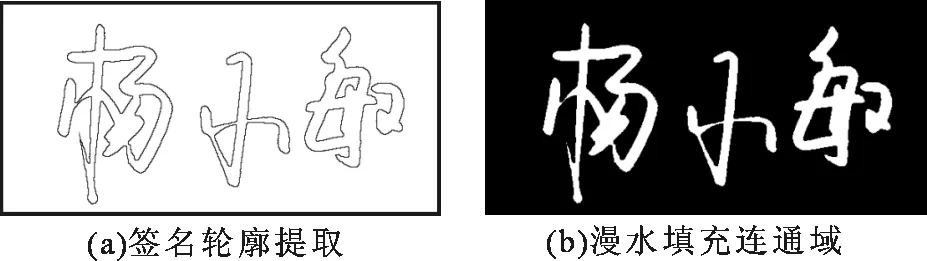
图3 漫水填充与轮廓提取连通域Fig.3 Connected domain of diffuse water filling and contour extraction

2.1.3 签名交叉点和端点数 关于不同人书写的同一签名,其笔划交叉点以及端点的个数之间都会存在一定的差别。因此,我们可以用具有单像素宽度的签名骨架上的端点和交叉点作为一组有效的局部特征。文中将交叉点分为3种,分别为二交叉点、三交叉点,以及四交叉点。在以像素点(i,j)为中心的3×3邻域进行二值骨架的扫描和判断,如图4所示。在3×3像素邻域图中,我们定义了8组像素对,分别是:A:{(i-1,j-1),(i,j)},B:{(i-1,j),(i,j)},C:{(i-1,j+1),(i,j)},D:{(i,j+1),(i,j)}，E:{(i+1,j+1),(i,j)},F:{(i+1,j),(i,j)},G:{(i+1,j-1),(i,j)},H:{(i,j-1),(i,j)}。当这些像素对之间满足如下规则L1～L4时,则判定其中心像素点(i,j)为相应交叉点类型。

端点与交叉点的定义:

L1:上述8组像素对中,若只有1对像素值为1,则判定中心像素点(i,j)为端点。

L2:上述定义的8组像素对中,除了一条直线上的像素对之外,例如A和E，B和F，C和G，D和H,剩余任意两组像素对的值都为1时,则判定中心像素点(i,j)为折点或者拐点。

L3:上述8组像素对中,若任意3组中像素值全为1时,则判定像素点(i,j)为三叉交点。

L4:上述8组像素对中,若任意4组中像素值全为1时,则判定像素点(i,j)为四叉交点。

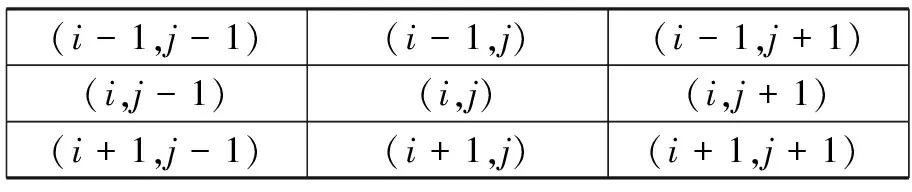
(i-1，j-1)(i-1，j)(i-1，j+1)(i，j-1)(i，j)(i，j+1)(i+1，j-1)(i+1，j)(i+1，j+1)

图4 像素邻域分布示意图

Fig.4 Pixel neighborhood maps

2.2 不变矩特征

矩特征的概念来源于物理力学,以图像像素为质点,以像素的坐标为力臂,将物理力学的阶矩借鉴过来以反映区域的形状特征。不变矩特征于20世纪60年代被提出,之后广泛用于字体识别中,具有平移、旋转,以及尺度缩放等不变性[12]。文中利用不变矩特征来反映物理意义明确的形状几何特征,例如字体相对重心,字形倾斜度,以及字形拉长度,因为这些几何特征可以从整体上有效地反映出书写者的运笔风格以及书写习惯。

首先定义一幅大小为M×N的签名图像f(x,y)的p+q阶矩Apq为

(1)

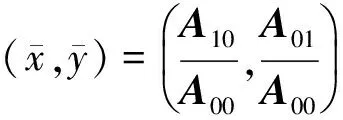
(2)

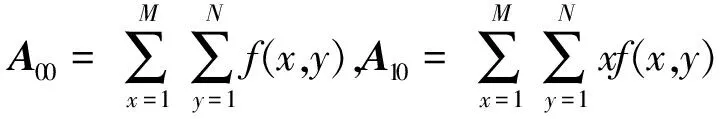
(3)

(4)

定义签名图像f(x,y)的p+q阶中心矩为

(5)

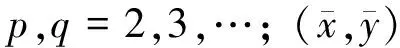
中心矩μpq表示签名图像区域相对于灰度重心的分布。二阶中心距μ00表示图像签名中所有像素点的灰度值之和。二阶中心矩μ20表示图像签名中沿x坐标方向的方差,其物理意义上表征字符图像在水平方向的伸展度。同理,μ02表征签名图像在垂直方向的伸展度。二阶中心距μ11表征图像签名的倾斜程度,基函数代表图像签名把重心作为原点分布。若μ11<0,则签名笔迹向右上方倾斜;若μ11>0,则签名笔迹向左上方倾斜。

签名字体倾斜度中，字符点阵协方差矩阵定义为

(6)

该字符点矩阵的正交轴就是协方差矩阵的特征向量,字符的伸展方向为特征值较大的主轴方向。因此,我们利用协方差矩阵可以计算主轴的方向角度θ，字形倾斜度ffqx,以及字形拉长度fflc,如下式

(7)

(8)

式(7)中，

若ffqx>0,则签名左倾斜;若ffqx<0,则签名右倾斜。在式(8)中，

本研究对二阶中心矩的字形倾斜度以及字形拉长度两个物理量进行了提取,加上之前的相对重心量,共4维特征。

2.3 基于Gabor滤波的纹理方向特征

通过对大量样本的观察发现,由于签名书写的随意性,真实签名之间通常存在一定的差异性,同时模仿签名之间也存在一定的相似特性。尽管如此,书写的习惯性导致同一个人签名笔划的方向特征还是相对较稳定的。为了在频域中找到能反映细微边角差异的纹理特征量,可以利用多通道Gabor滤波器对图像签名进行预处理[13]。很显然,不同方向的频域滤波在一定程度上能够反映细微的签名频域特征。

2.3.1 Gabor函数 信号处理中存在着时域频域测不准关系的问题,即时域上非常明确的信号特征,在频域内就会变得不确定，反之亦然。直到1964年,学者Gabor提出了可以满足时域频域测不准关系下界的函数式,该函数式在频域中通过对高斯函数的平移得到，

(9)

二维Gabor函数为一维Gabor函数在二维函数空间上的推广，

g(x,y)=

(10)

其中二维Gabor函数的傅里叶变换为

(11)

二维高斯函数实际上属于二维空间上的平滑函数,然而二维Gabor函数则是二维空间上的带通滤波器。和一维空间的情况一样,二维Gabor函数也满足时域频域测不准关系,也是唯一能达到不准下界的函数,因此利用二维Gabor滤波器的性质可以实现不同纹理信号分割,其基本原理就是可以较好地通过一类主频纹理,同时过滤掉另一类的主频纹理。

2.3.2 Gabor滤波器 本文采用Gabor滤波器的空域表达式为

G(x,y,f,θ)=

(12)

x′=xsinθ+ycosθ，

(13)

y′=xcosθ-ysinθ。

(14)

其中,f表示在θ方向上的正弦波频率,δx′,δy′分别表示沿着x′,y′方向的高斯方差,均为常量。

为了分辨各类真伪图像签名之间笔迹上的细微差异,我们构造了M×M的Gabor滤波器,其频率f为0.5,而x和y方向的δ方差分别为0.5和1,选取0,π/4,π/2,3π/4这4个不同的方向。

(15)

其中,ni代表子图Si中像素的个数,Piθ代表子图Si中像素fiθ(x,y)的均值。至此,针对每幅图像签名都可以得到一组4×N维的特征向量。N取值为8,因此每幅图像签名提取到Gabor滤波笔划的方向特征为32维。

最终,我们共提取到95维图像签名的静态特征量。其中包括签名形状特征9组共63维,签名纹理方向特征32维。

3 签名鉴别的分类

3.1 稀疏字典的设计

稀疏字典一般包括超完备字典和标准正交字典两种[14],标准正交字典大多都是通过字典学习算法得到,此外字典学习算法中求解出的稀疏系数中含有太多非零项,通常适合使用MOD算法，K-SVD算法,或者Online Dictionary Learning方法进行分类,不适合通过求解L1范数的稀疏表示进行分类。相对而言,超完备字典通常是由训练样本集的简单变换构成,冗余性比较强,能较好地稀疏表示测试样本,因此，文中选用超完备字典。

假设同一书写人签名的训练样本集有C类,可以将第i类的si个样本装备成矩阵Ai=[xi1,xi2,…,xisi],其中C∈{0,1},表示真假签名,s表示同一人的签名样本总数。xij∈Rt表示第i类的第j个样本,t代表样本特征维数。在签名鉴别过程中,假设训练集D∈Rt×s,所以,训练样本集可表示为

D=[A0,A1]=[x01,…,x0s0,x11,…,x1s1]。

(16)

测试样本y可表示为训练样本集的线性组合，

y=Dx0。

(17)

3.2 稀疏系数求解

L1范数问题具有比L0范数更容易求解、比L2范数所求解更稀疏等优点,目前大部分稀疏系数求解问题都是基于解决L1范数最小化问题[15]。本文实验中的稀疏分类也应用L1范数问题。求解公式为

(18)

其中,‖x‖0代表L0范数,即非0元素的个数。然而,当训练样本集D为一超完备字典时,式(18)的求解就变成了NP难问题。数学上一般利用近似求解解决此类问题,通过求解L1范数稀疏系数来逼近L0范数的解,而L1范数求解是一个凸优化问题,属于比较常见的优化模型。因此,上述优化问题又变成式(19)，

(19)

考虑到噪声等因素的影响,还需为式(19)添加正则约束项,得到新的优化模型为

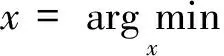
(20)

其中,ε代表噪声误差项。

3.3 稀疏分类方法选择

文中选择稀疏分类中经典的最小残差法和权重系数法对签名训练样本进行鉴别分类。

最小残差法(Min-error)的原理是利用所测试样本与它对应的恢复样本之间的残差来确定所属分类。

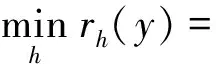
(21)

1)给定同一人签名训练集D=[A0,A1]=[x01,…,x0s0,x11,…,x1s1],已知测试样本y∈Rk,噪声误差项ε。

2)归一化训练样本。

5)判定测试样本y所属分类h，

(22)

其中,si代表第i类的样本个数。

4 实验结果及分析

4.1 实验样本说明

实验利用系统的采集模块多次获取,共收集了11人不同时间段的自然手写签名。其中每个人的真实签名数40个，不同人书写的伪造签名数在60到75个之间,真实签名共计440个,伪造签名共计718个。伪造签名包括随机伪造和熟练模仿两种,其中每个人的熟练伪造签名30个。签名样本如图5所示。

图5 签名样本示意图Fig.5 Schematic diagram of signature samples

在实验中选取每人的20个真实签名和20个伪造签名(其中,随机模仿和熟练模仿各10个)作为训练样本,剩余的真假签名作为测试样本。因为共有11组签名,所以鉴别工作也分成11次,一次鉴别一个人的签名测试集。最终取11组签名的两类平均错误率FRR和FAR来评价模式分类方法的性能,其中 FRR表示错误拒绝的真实签名数与总体签名数的比值,FAR表示错误接纳的伪造签名数与总体签名数比值。对于理想系统,这两类错误率都应该可以忽略掉,但实际中,这两个指标是有相关性的:当拒真率(FRR)比较低时,纳误率(FAR)会比较高,反之亦然。

4.2 实验结果分析

在10组签名测试集上对Min-error和WC两种稀疏分类方法的FRR和FAR进行了实验,结果如表1所示，从表1可以看出，最小残差法的两类鉴别错误率明显低于权重系数法。

同时,为了验证本文L1范数稀疏表示分类的有效性,我们分别用经典KNN和SVM算法,以及稀疏分类的最小残差法(Min-error)对签名的静态特征进行分类错误率的实验,具体实验结果如图6和图7两个直观的错误率曲线图所示。

从图5和图6可以看出，文中所使用的稀疏表示最小残差法在FAR与FRR两类指标下都优于传统经典模式分类方法。稀疏分类最小残差法在本文相同的特征集下10组数据上的平均FRR为9.25%,平均FAR为4.63%。而采用经典KNN和SVM得到的平均FRR分别为12.15%和13.31%,平均FAR分别为8.67%和7.26%。结果表明,采用稀疏表示分类方法更具加有效,较经典方法提高了鉴别签名的精准度。

表1 最小残差法和权重系数法错误率实验结果

Tab.1 Experimental results on the error rate of Min-error method and WC method

签名ID 最小残差法Min-error 权重系数法WC FRRFAR平均FRRFAR平均10116700500008340133300667010002011290048400806014520048400968301290006450096801290006450096840076900769007690107700923010005004840016100323008060048400645601077004620077001077004620077070111100417007640138900556009738008330050000667010000066700834900676004050054100946006760081110007140028600500008570042900643

图6 KNN，SVM和Min-error误纳率比较Fig.6 Comparison of KNN, SVM and Min-error FAR

图7 KNN，SVM和Min-error拒真率比较Fig.7 FRR comparison of KNN, SVM and Min-error

5 结 论

文中在重点介绍了签名图像形状特征、纹理特征,以及不变矩特征3大静态特征的基础上,提出了签名图像纹理特征、不变矩特征以及形状特征中的字体骨架倾斜方向向量、签名网孔数和连通域数、签名交叉点及端点数等特征的提取方法和技术,在此基础上,利用基于L1范数的稀疏表示法对提取的图像特征集进行了签名鉴别分类。通过有效实验表明,利用文中所提出的形状特征以及纹理特征而生成的训练集,明显降低了签名鉴别的纳误率FAR和拒真率FRR。

[1] LÜ Hairong,WANG Wenyuan,WANG Chong,et al. Off-line Chinese signature verification based on support vectormachines[J].Pattern Recognition Letters,2005,26(15):2390-2399.

[2] KOERICH A L, SABOURIN R, SUEN C Y.Recognition and verification of unconstrained handwritten words [J].IEEE Transactions on Patten Analysis and Machine Intelligence,2005,27(10):1509-1522..

[3] 张大海,汪增福.用于在线签名认证的特征提取和个性化特征选择方法[J]. 模式识别与人工智能,2009,22(4):619-623.

[4] 王珂敏.基于 DTW改进算法的在线签名鉴别方法[J].科技导报,2010,28(13):101-104.

[5] 肖春景,乔永卫,贺怀清.基于小波包的手写体签名特征提取方法[J].中国民航大学学报, 2011,29(3):13-15.

[6] 陈晓红，贾玉文，杨旭，等.纸上静态签名笔迹动态特征的提取和分析[J].中国司法签定,2012(4):28-36.

[7] DARAMOLA S A, IBIYEMI S. Novel feature extraction technique for off-line signature verification system[J]. International Journal of Engineering Science and Technology, 2010,2(7):3137-3143.

[8] BLAYVAS I,BRUCKSTEIN A,KIRNMEL R. Efficient computation of adaptive threshold surfaces for image binarization[J]. Pattern Recognition, 2006,39(1): 89-101.

[9] 陈睿. 一种新型的手写汉字笔迹鉴别方法[J].西南大学学报(自然科学版)，2014,36(1):137-145.

[10] 左敏,曾广平. 基于等价对的图像连通域标记算法[J].计算机仿真，2011,28(1):14-16.

[11] 陈佳鑫,贾英民.一种基于满水填充法的实时彩色目标识别方法[J].计算机仿真,2012, 29(3):4-8.

[12] 张黎, 陈宇桐,李海伟. 一种基于不变矩的图像分类算法[J].大众科技,2014,16(9): 12-15.

[13] ZUO W,QI M. A novel data fusion scheme for offline Chinese signature verification[C]∥International Conference on Natural Computation. Springer Berlin Heidelberg, 2005:51-54.

[14] 易学能.图像的稀疏字典及其应用[D].武汉：华中科技大学，2011：2-11.

[15] 周崴.L1范数最小化算法及应用[D].广州：华南理工大学，2013：51-56.

(编 辑 李 静)

Static feature extraction technology of signature verification in mobile internet banking

HE Dianyuan, FENG Jun, YANG Xiaomeng

(School of Information Science and Technology, Northwest University, Xi′an 710127， China)

Based on the research on the preprocessing of signature image, a new research approach that the static characteristics of signature images are obtained by extracting the shape features of the image, the invariant moments features of the image and the features of texture direction based on the Gabor filter in the image is proposed. Signature verification is carried out on the set including 10 feature samples extracted by the L1 norm classification method based on sparse representation. The experimental results show that the average FRR and the average FAR of Min-error method for the sparse classification are 9.25% and 4.63%, respectively. They are significantly lower than 12.15% and 8.67%, respectively for classical KNN method, and 13.31% and 7.26%, respectively for classical SVM method. The research results can meet the performance requirements of mobile internet banking.

internet banking; static feature； extraction technology; L1 norm; sparse representation

2016-03-07

何殿源，男，内蒙古呼和浩特人，博士生，从事模式识别及金融大数据研究。

TP391

A

10.16152/j.cnki.xdxbzr.2016-06-006