癫痫脑电的特征提取方法综述

张 瑞,宋江玲,胡文凤

(西北大学 医学大数据研究中心，陕西 西安 710127)



【数理科学·脑电数据分析专题研究】

癫痫脑电的特征提取方法综述

张 瑞,宋江玲,胡文凤

(西北大学 医学大数据研究中心，陕西 西安 710127)

癫痫是一种常见的以反复癫痫性发作为特征的慢性神经系统疾病。癫痫性发作的自动检测是通过机器学习及数据挖掘等方法对癫痫发作脑电自动识别的一种技术。如何设计合适的脑电特征提取方法是有效完成癫痫性发作自动检测的关键所在。文中系统总结了用于癫痫性发作自动检测的脑电特征提取方法,分别从时域分析、频域分析、时频分析、非线性动力学、图论、癫痫计算模型6个方面将已有的癫痫脑电特征提取方法进行归类,并对每类方法的基本原理和设计思想进行了系统的阐述。

癫痫;癫痫性发作;脑电;自动检测;特征提取

癫痫是一种以突然、短暂、反复的癫痫性发作为特征的慢性神经系统疾病或综合征。癫痫性发作则是大脑内神经细胞群阵发性异常超同步电活动的临床表现。由于这种异常电活动的起始部位及传播方式不同, 导致癫痫临床表现复杂多样, 包括短暂的感觉障碍、肢体抽搐、意识丧失、行为障碍等。反复、突然的癫痫性发作十分危险, 严重威胁着人们的日常生活乃至生命, 且患者过早死亡的可能性是正常人的两到三倍[1]。因此, 关于癫痫有效诊断和治疗的研究具有非常重要的临床意义和社会意义。

脑电图 (electroencephalogram,EEG) 是大脑神经细胞群电生理活动的记录, 包含大量的生理及病理信息。它不仅是研究脑科学的重要工具, 而且是协助医师对神经系统疾病 (如癫痫、阿尔兹海默症、精神分裂症等) 进行诊断和治疗的主要方法之一。特别是对于癫痫, 脑电图更是其他方法所不能取代的检测手段之一。 EEG用于研究癫痫已有70多年的历史, 包括对癫痫性发作的检测、预测, 以及癫痫病灶的定位等。其中, 癫痫性发作的准确检测是进一步进行发作预测以及病灶定位的关键。

传统的癫痫性发作检测主要是依靠有经验的医生询问患者的临床病史,进而从视觉上检查EEG中是否存在癫痫性脑波来完成的。由于癫痫的发作时间具有不确定性, 因此往往需要对病人的脑电波进行长期监测, 这样就会产生海量的脑电数据, 从而使得传统的视觉检测方法变得十分耗时; 此外, 该方法又严重依赖于医生的个人经验, 因而主观性很强。为了克服上述局限性, 近年来关于癫痫性发作的自动检测成为一个研究热点问题。

癫痫性发作的自动检测主要是通过机器学习及数据挖掘等方法, 并借助计算机技术完成对EEG中有效信息的挖掘与提取, 以实现对癫痫发作脑电自动识别的一种技术。利用EEG进行癫痫性发作的自动检测, 其本质可归结为一个模式识别问题。具体流程如图1所示。

图1 癫痫性发作自动检测流程图Fig.1 Flow chart of automated seizure detection

在上述实现过程中,如何设计有效的、能够用于区分癫痫发作与未发作脑电的特征提取方法可认为是完成最终目标的关键所在。基于此,本文将从基于时域分析、频域分析、时频分析、非线性动力学、图论以及基于模型等6个方面对癫痫性发作自动检测中的脑电特征提取方法进行综述。

1 癫痫脑电的特征提取方法

1.1 基于时域的特征提取方法

早期关于癫痫脑电的特征提取基本都是源于对EEG中最基本的特征属性进行刻画。具体地,把EEG看作是一个时间序列同时计算该序列的相关统计量,并基于此定义对应的癫痫脑电特征。

1)基于序列的波形特征分析:Gotman于1982年提出了最早的最具代表性的基于脑电信号棘波-尖波的癫痫性发作自动检测方法[2]。在该方法中,首先将EEG分解为半波, 进而计算其波峰幅度、平均时长、 斜率、 变异系数等特征, 并与提前定义的阈值进行比较,从而完成对发作脑电的自动检测。

2)基于序列的互相关性分析:相关性分析是研究两随机变量间相关关系的统计方法,其中最常用的度量指标为互相关函数。在文献[3]中, Chandaka等人通过互相关函数计算参考EEG信号(通常为发作间歇期脑电)与当前EEG信号间的一族互相关系数值, 构成互相关序列, 进而从互相关图中提取图心(centroid)、等效宽度(equivalent width)、均方坐标(mean square abscissa)等指标, 构建基于互相关序列的脑电特征提取方法。

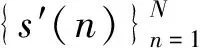
e(n) =s(n)-s′(n)=

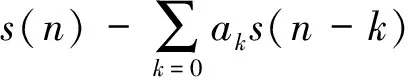
1.2 基于频域的特征提取方法

基于频域特征提取方法的主要思想是通过刻画信号在频域上的能量变化以提取相应的脑电特征。其中最常用的能量特征为功率谱(power spectral density,PSD), 它表示了信号功率随着频率的变化情况(即信号功率在频域的分布状况)。 由于癫痫发作时, 脑电信号的功率或能量相比未发作时会明显增大, 因此将脑电信号的功率谱作为特征能有效区分发作与未发作脑电。 图2中显示的是对应正常、发作与未发作脑电的功率谱,可以看出它们具有明显的差异性。

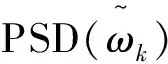
其中M为第p个数据上总的样本点个数,K为总的数据段个数[6]。 将计算出的功率谱值直接作为脑电特征,并结合分类器共同完成癫痫性发作的自动检测[7]。

2)基于参数方法的谱特征提取:包含基于AR，MA模型的参数方法, 特征向量法(eigenvector (EV))及多信号分类(multiple signal classification (MUSIC)等。 其中AR是一种最常用的基于模型的谱估计方法。假设样本来自于一个p阶的AR模型, 即

其中w(n)方差为σ2的白噪声。此时,功率谱密度定义为

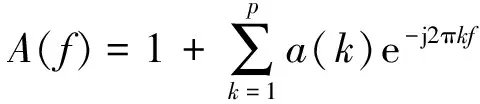
显然,只要估计出AR模型的参数a(k),即可求得相应功率谱密度的估计。 而AR参数的估计主要有Burg方法和Yuler-Walker方法。 可以将通过非参方法计算出的功率谱直接作为脑电特征，并结合分类器共同完成癫痫性发作的自动检测[8]。

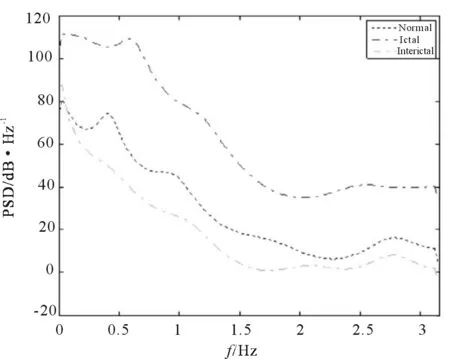
图2 正常、发作与未发作脑电的功率谱Fig.2 Power spectrum to normal, inter-ictal and ictal EEGs

3)基于谱值的癫痫脑电特征提取:除了上述工作中直接把计算出来的谱值作为癫痫脑电特征之外,在功率谱的基础上进一步处理以提取更有效的癫痫脑电特征,也是一个研究方向。Naghsh-Nilchi等人首先将脑电信号分解为不同频率子带(δ, θ,α,β,γ), 其次以EV和MUSIC方法得到每一子带的功率谱, 并从每个子带的功率谱中提取相应的均值、标准差、 熵 (entropy)、移动性(mobility)等参数, 最终将所有子带的参数进行整合作为最终分类癫痫脑电的特征集合[9]。

1.3 基于时频分析的特征提取方法

上述基于时域或频域的癫痫脑电特征提取方法,仅能反映脑电信号单一方面的特性,且常常需要假定信号是平稳或近似平稳的,这一假设显然与脑电信号的非平稳本质不符。为了克服这一局限性,许多研究者开始展开基于时频分析的癫痫脑电特征提取方法研究。

从时频分析角度分析EEG, 其主要观点是通过短时傅里叶变换(short-time wavelet transform,STFT)[10]、小波变换(wavelet transform,WT)[11-13]、 Hilbert-Huang变换[14-16]、经验模态分解(empirical mode decomposition, EMD)[17-18]等常用的非平稳信号分析方法对EEG信号进行重新表示, 并在此基础上进一步提取相应的特征。

1)基于WT的癫痫脑电特征提取: 小波变换是一种用于非平稳信号的时间-尺度分析手段, 在时域、频域都具有表征信号局部特征的能力[19]。 2006年,Jahankhani等人利用离散小波变换 (discrete wavelet transform, DWT)将EEG分解为不同的频率子带信号, 进而计算小波系数的最大值、最小值、均值、方差, 并将其作为脑电特征[20]。 Guo等人以子带信号的线长特征 (line length feature)作为所提取的癫痫脑电特征, 并结合神经网络完成癫痫性发作的自动检测[14]。 除线长特征外,Ocak等人从DWT分解后的子带信号中提取近似熵以完成癫痫性发作的自动检测[21]。离散小波包变换(wavelet package transform, WPT)作为WT的扩展, 也被用于脑电特征的提取。 Acharya等人通过WPT将EEG分解为子带信号后,将子带信号的高阶累积量作为脑电特征完成发作检测[22]。

2)基于EMD的癫痫脑电特征提取: EMD是Huang 于1998年提出的一种用于分析非平稳信号的方法[23], 它能够自适应地将信号分解为有限个数的本征模函数(intrinsic mode function,IMF)。 Li等人从EMD分解后的各IMF中提取方差、波动指标等特征[17],提出了一种新的癫痫脑电特征提取方法。 Pachori等人则将IMF二阶差分图的95%置信椭圆面积作为脑电特征, 以实现癫痫性发作的自动检测[18]。

1.4 基于非线性分析的特征提取方法

基于人们对脑科学研究的不断探索, 大量研究表明，大脑可以看作是一个非线性动力系统。 在这一背景下, 通过刻画非线性动力学特征以挖掘癫痫发作脑电与未发作脑电的差异性就成为近年来的研究热点问题。

1)基于系统的复杂性分析:神经科学研究表明,相比于正常脑电,癫痫发作时大脑的电活动变得相对简单,从而脑电信号的复杂性降低。基于这一理论,大量关于刻画非线性系统复杂性(或无规律性)的特征提取方法被广泛提出,其中最常见的一类即为基于熵的特征提取方法。20世纪90年代初,Pincus从衡量时间序列复杂性角度提出并发展了近似熵 (approximation entropy, ApEn) 的概念,并成功将它应用于生理性的时间序列分析,如心率信号、血压信号等[24]。直观地说,近似熵能够表示新信息的产生率,即近似熵越大,序列中新信息的产生率越大, 从而表明序列的复杂性越高。 然而,在原始近似熵的计算中不仅存在着自相似的比较,而且整个计算过程是一个极限过程,其值与数据长度有关。 这些因素都会导致近似熵值的偏差性。基于此, Richman和Moornan提出了一种新的度量时间序列复杂度的指标,即样本熵[25]。 Yuedong Song 等人分别以近似熵、样本熵作为脑电信号特征用于癫痫性发作的自动检测[26]。 排列熵是近期提出的一种新的度量时间序列复杂性的指标,它将信号映射到符号序列上后,通过对不同符号相对发生率的衡量来度量信号的复杂性。 Nicolao等人以排列熵为特征进行癫痫EEG的自动识别[27]。 类似地, 小波熵、谱熵、模糊近似熵等也作为脑电特征应用于癫痫性发作检测[28]。 除此之外关联和[29]、 线长特征[14]、 分形截距[30]等作为系统复杂性的度量也是癫痫性发作自动检测中常用的特征提取方法。

2)基于系统的反持久性分析:针对于癫痫未发作期脑电信号的反持久性低于发作期这一认知,大量对信号持久性刻画的脑电特征被提出。Hurst指数[31]是对序列随机性或长程相关性(持久性)的一种刻画指标。 它能揭示时间序列中的趋势性,并且通过值的大小反映时间序列持久性或反持久性的强弱,即值越接近1,持续性越强:越接近0,反持续性越强。 去趋势波动指标[32]是通过对序列的局部趋势进行线性拟合, 并计算信号与局部趋势间的均方误差, 然后基于均方误差构造出的能够反映时间序列长程相关性的另一种度量。 Qi Yuan 等人采用Hurst 指数及去趋势标度指数作为EEG特征进行癫痫性发作的自动检测[33]。

3)基于系统的同步性分析:由于癫痫性发作的本质是由神经细胞群超同步放电产生,因此在发作过程中系统的同步性必然高于未发作时期,因此基于系统同步性的度量可用于癫痫EEG的检测。 Mormann等人以脑电的相位同步性为特征, 检测颞叶癫痫病人的癫痫发作情况[34]; Altenburg用同步似然性作为EEG 通道间同步性的度量, 来辨别婴儿EEG 中的癫痫发作与未发作脑电[35]。 同步性也常被用于癫痫性发作的预测, Mirowskil等人以4种同步性度量(最大互相关指数, 非线性相互依赖性, 短期Lyapunov 指数的差异性, 基于小波的同步性度量)作为EEG特征来预测癫痫性发作[36]。

4)基于系统的非高斯性分析:由于癫痫发作时,脑电信号的高斯性明显强于未发作状态，因此，通过刻画系统的高斯性(或非高斯性)也构成了一种特性提取方法。高阶谱(high order spectra, HOS)是高阶统计量(三阶及三阶以上的矩或累积量)的谱表示, 它能够用于度量信号的非高斯性,并且能够从混合的非高斯性信号(各信号是独立的)和高斯噪声中分离出非高斯信号[37-38]。 实际应用中常用的是三阶矩的谱特征,即所谓的双阶谱。 双阶谱在二维频率图上给出了频率成分间的互相关性,它是关于两个频率变量的函数,很多有用的参数能够从双阶谱中提取出来。 Chua等人将从双阶谱中得到3个特征(平均谱幅、双阶谱熵、双阶谱平方熵)用于癫痫性发作前期、发作期以及正常脑电的检测[39]。 高阶累积量作为高阶统计量的非线性组合, 也常用于分析EEG信号或癫痫脑电的检测[39]。

1.5 基于图论的特征提取方法

从图论角度分析EEG, 关键在于将EEG首先表示为合适的图, 如星型图、局部二值模式、水平可视图等, 进而从图像处理的角度提取能够判别癫痫EEG的特征。

1)基于星型图拓扑指标的癫痫脑电特征提取:在星型拓扑结构中,各节点通过点到点的方式连接到一个中央节点上,其中任何两个节点要进行通信都必须经过中央节点。利用星型图分析脑电信号分为3个步骤:i) 根据脑电信号的幅度, 采用S2SNet滤波器将信号转化为字符串或序列; ii)将得到的字符序列转化为嵌入(embedded SG)和非嵌入的星型图 (non-embedded SG),如图3所示; iii) 计算相应的星型图拓扑指标(如连通矩阵的迹、Wiener指标、Harary数等)。 Blanco等人利用星型图拓扑指标及线性判别分析完成了癫痫性发作脑电的自动检测[40]。

2)基于局部二值模式的癫痫脑电特征提取:局部二值模式(local binary pattern, LBP)是一种纹理度量算子。 由于其原理相对简单、计算复杂度低、且具有旋转不变性和灰度不变性等优点, 因而在纹理分类、人脸识别、图像恢复等领域LBP方法都得到了广泛应用。 在一个图像中,LBP用于提取以某一像素为中心的领域内的像素强度变化情况, 并以简单的形式表示出来, 这使得其十分适用于非平稳信号的局部特性分析。 Kumar等人以癫痫发作与未发作脑电信号的一维LBP值作为脑电特征, 完成了癫痫性发作的自动检测[41]。

3)基于加权水平可视图的癫痫脑电特征提取:水平可视图(horizontal visibility graph, HVG)作为可视图的子图由Luque等人提出[42],是复杂网络的一种形式。 它将时间序列{xi}(i=1,2,…,n)转化为一个图G(V,E), 其中xi对应于图中的节点vi∈V, 而两点xi与xj间的关系对应于图中的一个边eij∈E。 由于节点自由度(即与某一节点相连的边的个数)难以区分具有单调性的时间序列及恒常数的时间序列[43], 而在EEG中包括棘波在内的大量波形都含有单调上升或下降的部分, 因此为了更好地检测癫痫发作时脑电中的棘波, Zhu等人提出了快速加权水平可视图(weighted horizontal visibility graph,WHVG)的方法, 并从得到的WHVG中提取出两个特征(平均自由度与平均强度)来区分发作脑电与正常脑电[43]。

图3 脑电片段的嵌入和非嵌入星型图Fig.3 Embedded and Non-embedded star graph of EEG segments

1.6 基于模型的特征提取方法

上述特征提取方法主要是从信号处理角度出发分析EEG。 然而,对于本身极其复杂的脑电信号而言, 已有的特征提取方法只能局限、片面地反映脑电的某一变化情况。 为了解大脑内在的生理变化过程与EEG间的关系, 进而从大脑的内在放电过程出发分析EEG, 显然有助于更全面、更本质地刻画大脑的放电过程。 从这一目标出发,大量学者提出了基于计算模型的脑电信号特征提取方法。 这一研究方向属于神经计算科学的范畴, 包含微观(主要考虑单个神经元的放电行为)和宏观(主要考虑由神经细胞经相互作用而构成群体的放电行为)两个层面。

神经生理学假定电极处检测到的大脑局部场电位是由大脑内部不同神经集群相互作用(主要是突触间的相互作用)而产生,当这种相互作用发生异常时,大脑内的放电也会发生异常。 在癫痫性发作的自动检测中,基于模型的特征提取方法,主要是通过对大脑神经集群间的相互作用进行建模,如Jasen模型、头皮丘脑模型等[44-47]。 通过分析模型中的生物物理参数,并根据参数的变化情况来发现大脑活动的异常。 Aarabi等人在Jasen模型的基础上进行扩展, 得到如图4所示的神经质量模型, 模型对应一组二阶常微分方程, 进而通过频域贝叶斯反演的方法估计微分方程中的参数,基于模型参数构造了用于癫痫性发作自动检测的特征[44]。

除了从上述角度出发,提取用于癫痫性发作的脑电特征之外,还有大量基于其他分析角度的癫痫脑电特征提取方法。 如Saab等人提出的用于临床或在线的癫痫发作检测系统,即通过Bayesian公式计算先验概率来判断癫痫发作与否[48]。 Rangaprakash等人基于递归量化分析(recurrence quantification analysis,RQA)与相位同步度量来研究大脑的连通性,通过大脑连通性的变化来检测癫痫的发作[49]。 Shasha Yuan等人将热力学中的扩散距离作为特征从脑电信号中提取出来, 进而结合贝叶斯线性判别分析完成癫痫性发作的自动检测[50]。

2 总 结

癫痫性发作的自动检测主要通过机器学习及数据挖掘等方法, 并借助计算机技术完成对EEG中有效信息的挖掘与提取, 以实现对癫痫发作脑电自动识别的一种技术。 如何设计有效的、能够用于区分癫痫发作与未发作脑电的特征提取方法是完成癫痫性发作自动检测的关键所在。 基于此,本文从时域分析、频域分析、时频分析、非线性动力学、图论以及计算模型等6个方面对已有的用于癫痫性发作自动检测的脑电特征提取方法进行综述,对每类方法的基本原理于设计思想步骤进行了系统阐述。

[1] ACHARYA U R, SREE S V, SWAPNA G, et al. Automated EEG analysis of epilepsy[J] .A Review, Knowledge-Based Systems, 2013,45:147-165.

[2] GOTMAN J. Automatic recognition of epileptic seizures in the EEG, Electroencephalogr[J] .Clin Neurophysiol, 1982,54:530-540.

[3] CHANDAKA S, CHATTERJEE A, MUNSHI S. Cross-correlation aided support vector machine classifier for classification of eeg signals[J] .Expert Systems with Applications, 2009,36:1329-1336.

[4] ALTUNAY S, TELATAR Z, EROGUL O. Epileptic eeg detection using the linear prediction error energy[J] .Expert Systems with Applications, 2010,37:5661-5665.

[5] JOSHI V, PACHORIA R B, VIJESH A. Classification of ictal and seizure-free EEG signals using fractional linear prediction[J] .Biomedical Signal Processing and Control, 2014,9:1-5.

[6] ALKAN A, KOKLUKAYA E, SUBASI A. Automated seizure detection in eeg using logistic regression and artificial neural network[J] .Journal of Neuroscience Methods, 2005,148:167-176.

[7] POLAT K, GUNES S.Classification of epileptiform EEG using a hybrid systemsbased on decision tree classifier and fast Fourier transform[J] .Appl Math Comput,2007,187(2):1017-1026.

[8] SUBASI A, ERCELEBI E, ALKAN A, et al. Comparison of subspace-based methods with parametric methods in epileptic seizure detection[J] .Computers in Biology and Medicine, 2006,36:195-208.

[9] NAGHSH-NILCHI A R, AGHASHAHI M. Epilepsy seizure detection using eigen-system spectral estimation and multiple layer perceptron neural network[J] .Biomedical Signal Processing and Control, 2010,5:147-157.

[10] KIYMIK M K,GULER I, DIZIBUYUK A, et al. Comparison of STFT and wavelet transform methods in determining epileptic seizure activity in EEG signals for real-time application[J] .Computers in Biology and Medicine,2005,35:603-616.

[11] JAHANKHANI P, KODOGIANNIS V, REVETT K. EEG signal classification using wavelet feature extraction and neural networks[M] .in: IEEE International Symposium on Modern Computing John Vincent Atanasoff, 2006:120-124.

[12] SADATI N, MOHSENI H R, MAGSHOUDI A. Epileptic seizure detection using neural fuzzy networks[M] .in: Proceedings of the IEEE International Conference on Fuzzy Systems, 2006:596-600.

[13] SUBASI A.EEG Signal classification using wavelet feature extraction and a mixture of expert model[J] .Expert Syst Appl,2007,32 (4):1084-1093.

[14] GUO L, RIVERO D, DORADO J, et al. Automatic epileptic seizure detection in EEGs based on line length feature and artificial neural network[J] .Journal of Neuroscience Methods, 2010,191:101-109.

[15] KUMAR Y, DEWAL M L, ANAND R S. Epileptic seizure detection using dwt based fuzzy approximate entropy and support vector machine[J] .Neurocomputing, 2014,133:271-279.

[16] ORHAN U, HEKIM M, OZER M. EEG signals classification using the k-means clustering and a multilayer perceptron neural network model[J] .Expert Systems with Applications, 2011,38:13475-13481.

[17] LI S, ZHOU W, YUAN Q, et al. Feature extraction and recognition of ictal eeg using EMD and SVM[J] .Computers in Biology and Medicine, 2013,43:807-816.

[18] PACHORI R B, PATIDAR S.Epileptic seizure classification in EEG signals using second-order difference plot of intrinsic mode functions[J] .Computer Methods and Programs in Biomedicine,2014，113(2)：494-502.

[19] MALLAT S. A theory for multiresolution signal decomposition: the wavelet representation[J] .IEEE Trans Pattern Anal March Intell, 1989,11(7):674-693.

[20] JAHANKHANI P, KODOGIANNIS V, REVETT K.EEGsignal classification using wavelet feature extraction and neural networks[M] . In: IEEE John Vincent Atanasoff 2006 International Symposium on Modern Computing (JVA’06); 2006:52-57.

[21] OCAK H. Automatic detection of epileptic seizures in EEG using discrete wavelet transform and approximate entropy[J] .Expert Syst Appl,2009,36 (2):2027-2036.

[22] ACHARYA U R, VINITHA S, SREE J , et al.Automatic detection of epileptic EEG signals using higher order cumulant features[J] .Int J Neural Syst,2011,21 (5):1-12.

[23] FLANDRIN P, RILLING G, GONCALVES P. Empirical Mode Decomposition as a Filterbank[J] .IEEE Signal Processing Letters, 2003,2:112-114.

[24] PINCUS S M,GLADSTONE I M,EHRENKRANZ R A. A regular statistic for medical data analysis[J] .Journal of Clinical Monitoring. 1991,4:335-345.

[25] RICHMAN J S, MORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J] .American Journal of Physiology: Heart and Circulatory Physiology,2000,6:2039-2049.

[26] SONG Y, CROWCROFT J, ZHANG J. Automated epileptic seizure detection in EEGs based on optimized sample entropy and extreme learning machine[J] .Journal of Neuroscience Methods, 2012,210:132-146.

[27] NICOLAOU N, GEORGIOU J. Detection of epileptic electroencephalogram based on permutation entropy and support vector machines[J] .Expert Systems with Applications, 2012,39:202-209.

[28] KUMAR S P, SRIRAAM N, BENAKOP P, et al.Entropies based detection of epileptic seizures with artificial neural network classifiers[J] .Expert Systems with Applications, 2010,37: 2010, 3284-3291.

[29] TITO M, CABRERIZO M, AYALA M, et al. Classification of electroencep-halographic seizure recordings into ictal and inter-ictal files using correlation sum[J].Computers in Biology and Medicine, 2009,39:604-614.

[30] YUAN Q, ZHOU W D,LIU Y X , et al.Epileptic seizure detection with linear and nonlinear features[J] .Epilepsy & Behavior,2012,24:415-421.

[31] HURST H E. Long-term storage capacity of reservoirs[J] .Transactions of the American Society Civil Engineers, 1951,116:770-779.

[32] PENG C K, BULDYREV S V, HARLIN S. Mosaic organization of DNA nucleotides[J] .Phys Rev E,1994,2:1685-1689.

[33] YUAN Q, ZHOU W, LI S, et al. Epileptic eeg classification based on extreme learning machine and nonlinear features[J] .Epilepsy Research, 2011,96:29-38.

[34] MORMANN F, LEHNERTZ K, DAVID P, et al. Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients[J] .Physica D, 2000,144:358.

[35] ALTENBURG J, VERMEULEN R J, ROB L M, et al. Seizure detection in the neonatal EEG with synchronization likelihood[J] .Clinical Neurophysiology,2003,114:50-55.

[36] MIROWSKI P, MADHAVAN D, LECUN Y, et al. Classification of Patterns of EEG Synchronization for Seizure Prediction[J] .Clinical Neurophysiology,2009,120:1927-1940.

[37] ACHARYA U R, SREE S V, SURI J S. Automatic detection of epileptic EEG signals using higher order cumulant features[J] .Int J Neural Syst，2011,5:1-12.[38] YAO D. Electroencephalography inverse problem by subspace decomposition of the fourth-order cumulant matrix[J] .J Biomed Eng，2000,2:174-178.

[39] CHUA K C, CHANDRAN V, ACHARYA U R, et al. Application of higher order spectra to identify epileptic EEG[J] .J Med Syst, 2011, 6:1563-1571.

[40] FERNANDEZ-BLANCO E, RIVERO D, RABUNAL J, et al. Automatic seizure detection based on star graph topological indices[J] .Journal of Neuroscience Methods, 2012,209:410-419.

[41] KUMAR T S, KANHANGAD V, PACHORI R. B. Classification of seizure and seizure-free EEG signals using local binary patterns[J] .Biomedical Signal Processing and Control, 2015,15:33C40.

[42] LUQUE B, LACASA L, BALLESTEROS F.Horizontal visibility graphs: exact results for random time series[J] .Phys Rev E, 2009，17:80.

[43] ZHU G, LI Y, WEN P P.Epileptic seizure detection in EEGs signals using a fast weighted horizontal visibility algorithm[M] .Computers in Biology and Medicine, 2014:64-75.

[44] AARABI A, HE B. Seizure prediction in hippocampal and neocortical epilepsy using model-based approach[J] .Clinical Neurophysiology, 2014,125:930-940.

[45] WENDLING F, BENQUET P, BARTOLOMEI F, et al. Computational models of epileptiform activity[J] .Journal of Neuroscience Methods, 2016,260:233-251.

[46] AARABI A, HE B. A rule-based seizure prediction method for focal neocortical epilepsy[J] .Clinical Neurophysiology, 2012,123:1111-1122.

[47] HOCEPIED G, LEGROS B, VANBOGERT P, et al. Early detection of epileptic seizures based on parameter identification of neural mass model[J] .Computers in Biology and Medicine, 2013,43:1773-1782.

[48] SAAB M, GOTMAN J. A system to detect the onset of epileptic seizures in scalp EEG[J] .Clinical Neurophysiology, 2005,116:427-442.

[49] RANGAPRAKASH D. Connectivity analysis of multichannel EEG signals using recurrence based phase synchronization technique[J] .Computers in Biology and Medicine, 2014,46:11-21.

[50] YUAN S S, ZHOU W D, YUAN Q, et al. Automatic seizure detection using diffusion distance and BLDA in intracranial EEG[J] .Epilepsy & Behavior, 2014,31:339-345.

(编 辑 亢小玉)

A review of feature extraction method for epileptic EEGs

ZHANG Rui, SONG Jiangling, HU Wenfeng

(Medical Big Data Research Center, Northwest University, Xi′an 710127， China)

Epilepsy is a serious brain disorder characterized by recurrent and transient epileptic seizures. Automated epileptic seizure detection is the technique for recognizing epileptic EEGs automatically through the machine learning and data mining methods. How to design an appropriate feature extraction method plays a key role in realizing the seizure detection successfully. This paper systemically summarizes the fundamental theories and designing procedures of existing EEG feature extraction methods from the perspective of time-domain analysis, frequency-domain analysis, time-frequency analysis, non-linear dynamics, graph-domain analysis and computational models.

epilepsy; epileptic seizure; electroencephalogram (EEG); automated seizure detection; feature extraction

2016-04-03

国家自然科学基金资助项目(61473223)；陕西省自然科学基础研究计划基金资助项目(2014JM1016)

张瑞，女，陕西西安人，西北大学教授，博士生导师，从事机器学习理论与算法、脑电心电数据分析等研究。

O29

A

10.16152/j.cnki.xdxbzr.2016-06-001

【主持人语】 大数据时代的到来，意味着传统的思维方式和解决问题的方法将发生巨大改变。医学是关乎民生的重要领域，是社会发展的轴心。随着现代医学科学技术的飞速发展，所产生的各种医学数据呈现规模巨态、表征动态、价值稀态及结构多态等特点。那么，如何运用现代信息技术与方法对这样高复杂性的医学大数据进行分析与处理以挖掘其中潜在的规律和价值，则是大数据时代下以数据驱动为研究与发展方向的必然趋势。西北大学医学大数据研究中心以创建具有鲜明领域特色的融合数学、信息、医学及生物等多学科的交叉研究中心为总体目标，以医学大数据分析与挖掘为研究重点，积极开展机器学习理论与方法及其在医学大数据分析中的应用等方面的研究工作。中心目前主要针对脑电、心电及中药数据，开展关于癫痫性发作的自动检测及预测、自适应阵发性房颤的自动检测、神经生理系统建模、中药成分谱效关系建模等课题的研究。

本次“脑电数据分析”专题由西北大学医学大数据研究中心主任张瑞教授主持，主要针对癫痫性发作自动检测中的相关问题展开系统研究。包括癫痫脑电的特征提取方法综述、癫痫脑电信号的去噪方法研究、非平衡脑电数据的处理方法研究、新的癫痫脑电特征提取方法研究。特别是在“癫痫脑电的特征提取方法综述”一文中， 首次对已有的癫痫脑电特征提取方法， 分别从时域分析、 频域分析、 时频分析、 非线性分析、 图论、 癫痫计算模型6个方面进行归类， 并对每类方法的基本原理和设计思想进行了系统的阐述。 此外， 本栏目内容还包含了癫痫性发作自动检测中的去噪、 非平衡处理及特征提取等各个关键环节。 所提出的基于ICA与小波阈值的癫痫脑电信号去噪方法， 在一定程度上达到了自动去噪的效果， 同时避免了去噪过程中对噪声人工辨别及干净参考噪声选取等问题； 所提出的数据平衡方法， 在减少数据信息损失的前提下提高了非平衡数据分类的有效性； 所提出的癫痫脑电融合特征提取方法与已有方法相比， 检测性能有了很大提高， 准确率可达到97.42%。这些工作为癫痫性发作自动检测的系统研究提供了一定的思路。

主持人：张瑞，西北大学医学大数据研究中心主任，西北大学数学学院教授，博士生导师。