非平衡数据处理方法在癫痫发作检测中的应用

野梅娜,李艳艳,杨陈军,张 瑞

(西北大学 医学大数据研究中心,陕西 西安 710127)



·数理科学·脑电数据分析专题研究·

非平衡数据处理方法在癫痫发作检测中的应用

野梅娜,李艳艳,杨陈军,张 瑞

(西北大学 医学大数据研究中心,陕西 西安 710127)

非平衡数据集是指数据集中的某类样本数量远大于其他样本的数量。对于此类数据,类分布的不平衡会直接导致很多分类算法的失效。文中基于K-means聚类,Silhouette指标和M-近邻下采样提出一种新的数据平衡方法(K-S-M)。该方法首先用K-means算法对多数类样本进行多次聚类并选取最优聚类个数,然后采用M-近邻下采样对聚类后的数据进行采样,将采样后的点最终构成平衡数据,并对得到的平衡数据进行癫痫性发作的自动检测。实验结果表明,文中所提方法可以很好地处理非平衡数据,减少数据信息损失,同时可以提高非平衡数据分类的有效性。

非平衡数据集;Silhouette指标;K-means算法;M-近邻下采样;癫痫性发作;癫痫脑电信号

癫痫是由于大脑神经细胞群超同步放电引起的脑部神经系统紊乱疾病,具有反复性和突发性,严重危害人类健康。头皮脑电图是大脑细胞电生理活动的记录,由于其不开刀、花费小等特点,现已成为癫痫诊断和治疗的一个主要手段。但是,由于癫痫性发作的不确定性,往往需要对病人进行长时间的监测,而且在所记录的脑电数据中,非发作脑电数据量远远大于发作脑电数据量,从而会产生海量的非平衡脑电数据集。

非平衡数据集是指数据集中的某类样本数量远大于其他样本的数量,样本多的称为多数类,样本少的称为少数类[1]。对于此类数据,类分布的不平衡会直接导致很多分类算法的失效,而非平衡数据在众多实际问题中又普遍存在。 因此,如何提高非平衡数据集的分类性能成为一个研究热点问题。目前针对解决非平衡数据分类的问题主要包括数据处理以及算法设计两方面。在算法层面上[2-4],主要结合非平衡数据集的特点,对传统的分类算法进行改进,以提高相应的分类性能;在数据层面上[5-9],主要是对数据进行重新采样以达到平衡。采样方法分为欠采样和过采样两种。过采样是指增加少数类样本数量以达到平衡,欠采样则是降低多数类样本数量以达到平衡。传统的过采样技术由于并不产生新的样本,只是通过对原始的少数类样本进行复制,容易过学习现象[10]。最为广泛应用的欠采样方法为随机下采样,但该方法会造成重要数据的缺失。

本文提出了一种新的非平衡数据处理方法,并将该方法应用于癫痫性发作的自动检测。首先,应用Silhouette指标与K-means聚类相结合的算法对多类数据进行聚类并选取最优聚类个数;其次,采用M-近邻下采样方法对聚类后的数据选取具有代表性的样本点,将所选取样本点构成最终的平衡多类数据集;最后,结合3种脑电特征及超限学习机(ELM)完成癫痫性发作的自动检测。

1 方 法

1.1 K-means算法

K-means是一类基于距离的迭代式聚类算法。在该算法中,N个样本被分类到K个类中,以使每个样本与其所在的类中心比该样本与其他类中心的距离更小。

K-means算法:给定样本数据集S={s1,s2,…,sN},聚类个数K。

步骤1 从数据集中随机选出K个样本作为初始类中心;

步骤2 对剩余的样本,计算其到每个类中心的距离,并将其划分到距离最近的类中心所在的类中;

步骤3 计算每一类的样本均值,并将其作为新的类中心;

步骤4 重复步骤2，3,直到相邻两次总的类内误差不再发生变化。

1.2 Silhouette指标

在聚类方法中聚类个数K的选取十分重要,往往通常通过聚类有效性指标方法来确定最佳聚类个数。常用的包括Calinski-Harabasz指标、In-Group Proportion指标及Silhouette指标等。基于Silhouette指标的简单易行及有效性,本文采用Silhouette指标法,即通过计算每一样本与类内样本及类间样本间的距离来确定聚类个数K。

设K-means算法将数据集聚为K类,记为Ω={C1,C2,…,CK},其中Ck={sk,1,sk,2,…,sk,lk}表示此次聚类结果Ω中的第k类。显然有

其中sk,i为类Ck中的第i样本点。

首先定义点sk,i的Silhouette指标为[11]:

(1)

其次,定义聚类结果Ω={C1,C2,…,CK}的整体Silhouette指标为:

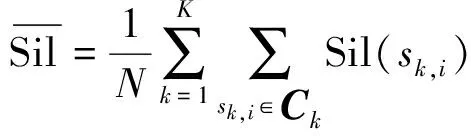
(2)

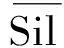
1.3 M-近邻下采样

文献[13]中已证明,类中心是各类中最富有代表性的样本。显然,与类中心最密切相关的点也能够在一定程度上表征一个聚类簇内样本的整体特性。本小节介绍基于类中心的M-近邻下采样方法,用以选取所有类中最具代表性的点构成新的数据集,从而达到平衡两类数据的目标。

M-近邻下采样算法:给定样本数据集S={s1,s2,…,sN}。根据K-means算法将数据集S聚为K类,记作:

Ω={C1,C2,…,CK},

其中Ck={sk,1,sk,2,…,sk,lk}(k=1,2,…,K)。

步骤1 计算Ck的类中心:

步骤2 计算Ck中的元素sk,i到类中心mk的距离:dki=d(sk,i,mk), i=1,2，…,lk;

步骤4 则数据集S的M-近邻下采样为:

综上所述，在白内障小切口手法超乳术中予以患者优质护理，可缩短手术时间，优化视力恢复程度，降低并发症发生率，提升护理满意度，效果可观。

1.4 一种新的数据平衡方法

在上述工作的基础上,本小节提出一种基于K-means,Silhouette指标和M-近邻下采样的新的数据平衡方法(K-S-M),并总结为如下算法。

数据平衡算法K-S-M:给定数据集Θ=SP∪SN,其中SP表示正类点集(多数类),SN表示负类点集(少数类); 聚类次数m;下采样参数p。

步骤1 采用K-means算法对正类点集SP进行第i次聚类,聚类结果记为:

Ωi={C1,C2,…,CKi}, i=1，2，…,m;

Cip;

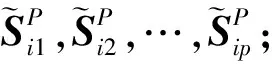
步骤7 将所提取的特征作为输入,应用超限学习机进行分类;

步骤8 根据分类结果选取最优聚类个数,记作k*,并记其所对应的聚类结果为Ωk*;

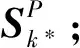
2 数据平衡处理方法K-S-M在癫痫性发作自动检测中的应用

癫痫的自动检测即通过挖掘EEG中潜在的癫痫样波特征,并结合某一分类器对EEG中是否有癫痫性发作进行判断。若将脑电分为发作脑电与未发作脑电,则其本质上就是一个两类分类问题。

2.1 特征提取

本文选用3种特征提取方法:线长L(line length)、均方根幅值RMS Amp(root mean square amplitude)以及Hjorth第3参数C(complexity)。

线长[14]是由Eteller等人提出的作为用于癫痫性发作的自动检测的脑电特征,其表达式为:

(3)

RMS Amp[15]是Maynard等人用于大脑功能检测仪中的输出估计,计算公式为:

(4)

Hjorth第3参数即复杂性(complexity)[16],是Hjorth在1970年提出的。若x(t)为癫痫脑电信号,则复杂性定义为:

(5)

其中σx”为x(t)的二阶差分的标准差。σx′为x(t)的一阶差分的标准差,σx为x(t)的标准差。

2.2 超限学习机

超限学习机(extreme learning machine, ELM)是由Huang等人于2006年提出的一种新的学习算法。不同于传统的学习方式, ELM 算法中的隐变量不再需要迭代而是随机产生[17]。与其他学习算法相比,ELM具有泛化能力强、速度快等优势。

(6)

其中wj=[w1j,w2j,…,wnj]T为连接输入层与第j个隐单元的权值向量;bj为第j个隐单元的阈值;βj=[βj1,βj2,…,βjm]T为连接第j个隐单元和输出层的权值向量;wj·xi表示wj与xi的内积。如果网络的实际输出等于期望输出,则可得如下含有N个方程的线性方程组:

Hβ=T。

(7)

其中

(8)

在ELM算法中,隐层输入权重与阈值随机选取,即隐层输出矩阵为已知。于是,训练网络就相当于求解线性方程组(7)。该线性方程组的最小范数最小二乘解可表示为:

(9)

其中H†为H的Moore-Penrosw广义逆。

2.3 癫痫性发作的自动检测

对于平衡后的数据,本文采用已有方法对脑电信号进行特征提取,并结合超限学习机完成检测。具体流程如图1所示。

图1 癫痫性发作的自动检测流程Fig.1 The diagram of automated epileptic seizure detection

3 数值实验结果与分析

本小节将通过数值实验验证,本文所提出的非平衡数据处理方法在癫痫性发作自动检测中的可行性与有效性。

3.1 脑电数据

本文所用的脑电数据来自于波士顿儿童医院的CHB-MIT公开数据库[18]。实验中采用的是chb08病人的23通道脑电数据,时长2个小时,期间共有2次癫痫性发作,采样率为256Hz。

3.2 实验结果与分析

首先对EEG信号进行加窗处理,将其划分为4s长的脑电片段,共包含1 692个未发作脑电片段和106个发作片段。

在癫痫性发作自动检测中,分类性能评价指标包括准确率(accuracy)、敏感度(sensitivity)以及特异度(specificity),计算公式如下:

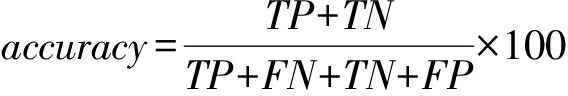
(10)

(11)

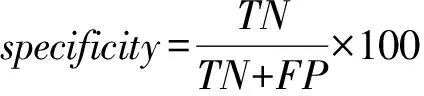
(12)

其中,TP(truepositive)为真阳性,表示发作信号被正确检测为发作;FN(falsenegative)为假阴性,表示发作信号被检测为未发作;FP(falsepositive)为假阳性,表示未发作信号被检测为发作;TN(truenegative)是真阴性,表示未发作信号被正确检测为发作。

数值实验结果如表1所示。从表1中可以明显看出:对于所有特征,采用未作平衡处理的脑电数据所得到的检测效果非常不好。主要表现为敏感度过低,直接导致漏检率很高,显然会为病人带来很大隐患。而这一现象也正是由于正类点样本过多所导致的。与随机下采样方法相比,采用本文方法处理后的平衡数据进行发作检测,其各项性能具有一定的提升。上述结果也可以通过ROC曲线说明。显然,ROC曲线下的面积(AUC)越大,表示分类性能越好。图2显示的分别是关于本文所提方法、随机下采样法以及未平衡处理的数据进行检测的ROC曲线。从图中可以明显看出,本文方法所获得的检测效果最好。

表1 3种癫痫性发作自动检测方法的性能比较

Tab.1 Performance comparison among three seizure detection methods

方法性能 未平衡处理 随机下采样 本文所提方法 CRMSLCRMSLCRMSL准确率/%91．9296．0793．4283．1585．6885．2886．0287．8187．04敏感度/%40．2051．1946．8082．0980．4486．7986．7983．9190．49特异度/%95．1798．8896．3585．1191．0184．0785．4291．6983．76

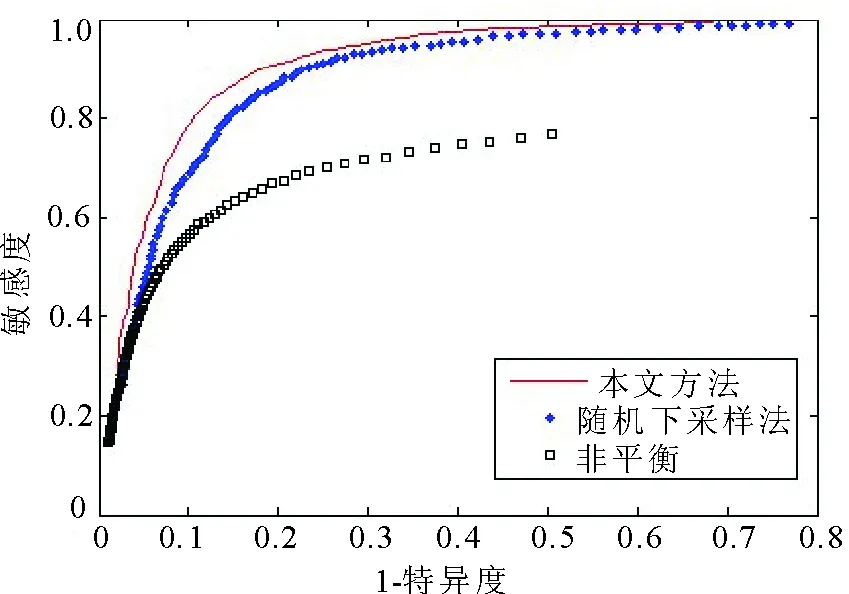
图2 数据平衡处理与未平衡处理的ROC曲线Fig.2 ROC curves corresponding to three methods

4 结 论

本文基于K-means算法,Silhouette指标以及M-近邻下采样提出了一种新的非平衡数据处理方法,并将该方法应用于癫痫性发作的自动检测。首先,应用Silhouette指标与K-means聚类相结合的算法对多类数据进行聚类并选取最优聚类个数;其次,采用M-近邻下采样方法对聚类后的数据选取具有代表性的样本点,将所选取样本点构成最终的平衡多类数据集;最后,结合3种脑电特征及超限学习机(ELM)完成癫痫性发作的自动检测。 CHB-MIT公开脑电数据库上的数值实验结果表明,本文所提出的非平衡数据处理方法在癫痫性发作自动检测应用中的性能良好,提高了非平衡数据的分类有效性。

[1] WEISS G M. Mining with rarity: a unifying framework [J]. SIGKDD Explorations, 2004, 6(1):7-19.

[2] 蒋莎, 张晓龙. 一种用于非平衡的SVM学习算法[J]计算机工程, 2008, 34(20): 198-199.

[3] WU G, CHANG E Y. Class-boundary alignment for Imbalanced dataset learning [J]. Icml Workshop on learning form Imbalanced Data Sets, 2003: 49-56.

[4] HUANG K, YANG H, KING I, et al. Imbalanced learning with a biased minimax probability machine [J].IEEE Transaction on System Man and Cybernetics, 2006, 36(4): 912-923.

[5] CHAWLA N V, BOWYER K W,HALL L O,et al. SMOTE: synthetic minority over-sampling technique [J]. Journal of Artificial Intelligence Research, 2011, 16(1): 321-357.

[6] 张健，方宏彬，孙启林，等.基于商空间理论的非平衡数据集分类算法[J].计算机应用, 2012, 32(1): 210-212.

[7] KUBAT M. Addressing the curse of imbalanced training sets: one-sided sampling [C]. International Conference on Machine Learning, 1997.

[8] YEN S J, LEE Y S. Cluster-based under-sampling approaches for imbalanced data distributions [J]. Expert Systems with Application an International Journal, 2009, 36(3):5178-5272.

[9] 张健, 方宏彬. 剪枝与采样相结合的不平衡数据分类方法[J]. 计算机应用研究，2012, 29(3): 847-848.

[10] 晁学鹏. 一种基于K均值聚类的下采样算法[J]. 科技通报，2013(8): 73-75.

[11] 王开军, 李健，张军英，等.聚类分析中类数估计方法的实验比较[J].计算机工程, 2008, 34(9):198-199.

[12] 付春梅, 刘俊宁, 张军英，等. K-means与系统聚类法结合在脑电图中的应用[J].科技信息，2007(29)：191-192.

[13] 胡小生, 张润晶，钟勇. 两层聚类的不平衡数据挖掘算 法[J].计算机科学，2013, 40(11):271-275.

[14] ESTELLER R, ECHAUZ J, TCHENG T, et al. Line length: an efficient feature for seizure onset detection [J]. Engineering in Medicine and Biology Society，2001(4)：335-342.

[15] MAYNARD D, PRIOR P F, SCOTT D F. Device for continuous monitoring of cerebral activity in resuscitated patients [J].British Medical Journal, 1969, 4:545-546.

[16] BO H. An on-line transformation of EEG scalp potentials into orthogonal source derivations [J]. Electroencephalography and Clinical Neurophysiology, 1975, 39(5):526-530.

[17] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: Theory and applications [J]. Neurocomputing,2006, 70(1-3):489-501.

[18] SHOEB A H, GUTTAG J V. Application of machine learning to epileptic seizure detection [C] International Conference on Machine Learning, 2010: 975-998.

[19] 周世兵, 徐振源, 唐旭清. 新的K-均值算法聚类数确定方法[J]. 计算机工程与应用，2010, 46(16):27-31.

(编 辑 亢小玉)

A new processing method of imbalance data and its application on the epileptic seizure detection

YE Meina, LI Yanyan, YANG Chenjun, ZHANG Rui

(Medical Big Data Research Center, Northwest University, Xi′an 710127， China)

Due to the imbalance distribution of data, many classical algorithms failed in realizing the classification for imbalance data sets, where the size of one class is much larger than that of another class. This paper proposes a novel data balance method K-S-M, which is based on the K-means clustering method, Silhouette index and M-neighboring under-sampling. The K-means method is first used repeatedly to cluster samples from the majority class, and the optimal number of clusters is determined based on the Silhouette index. Then the M-neighboring under-sampling method is applied to sampling from the obtained clusters; the balanced data set is next constructed, which includes such selected samples from majority class and the samples from the minority class. Finally, the epileptic seizure detection is completed on the balanced data set. Experimental results demonstrate that the proposed method improves the effectiveness of classification for imbalanced data.

imbalance data set; Silhouette index; K-means clustering method; M-neighboring under-sampling; epileptic seizure; electroencephalograph (EEG)

2016-03-19

国家自然科学基金资助项目(61473223)；陕西省自然科学基础研究计划基金资助项目(2014JM1016)

野梅娜，女，陕西西安人，从事非平衡数据处理与癫痫脑电信号自动检测研究。

张瑞，女，陕西西安人，西北大学教授，博士生导师，从事机器学习理论与算法、脑电心电数据分析等研究。

O29

A

10.16152/j.cnki.xdxbzr.2016-06-002