Subset-based localvs.finite element-based globaldigitalimage correlation:A comparison study

Bo Wng,Bing Pn,b,∗

aInstitute of Solid Mechanics,Beihang University,Beijing 100191,China

bState Key Lab of Automotive Safety and Energy,Department of Automotive Engineering,Tsinghua University,Beijing 100084,China

Review

Subset-based localvs.finite element-based globaldigitalimage correlation:A comparison study

Bo Wanga,Bing Pana,b,∗

aInstitute of Solid Mechanics,Beihang University,Beijing 100191,China

bState Key Lab of Automotive Safety and Energy,Department of Automotive Engineering,Tsinghua University,Beijing 100084,China

H I G H L I G H T S

.Performance evaluation ofsubset-based localand finite element(FE)-based globaldigitalimage correlation(DIC)is performed.

.Theoreticalanalyses ofthe standard deviation errors ofthe two DIC approaches are given.

.The performances oflocal DIC and global DIC approaches are compared with numericaltests and realexperiments.

.The results revealed that subset-based localDIC outperforms globalDIC when subset(element)size is larger than 11 pixels.

A R T I C L E I N F O

Article history:

Received 23 May 2016

Received in revised form

15 August 2016

Accepted 17 August 2016

Available online 24 August 2016

Digitalimage correlation Displacementmeasurement Finite element Subset Subpixel

Being the two primary approaches for full-field kinematics measurements,both subset-based localdigital image correlation(DIC)and finite element-based global DIC have been extensively studied.Nowadays, most commercial DIC systems employ local DIC algorithm because of its advantages of straight forward principle and higher efficiency.However,several researchers argue that global DIC can provide better displacement results due to the displacement continuity constraint among adjacent elements.As such, thoroughly examining the performance ofthese two different DIC methods seems to be highly necessary. Here,the random errors associated with local DIC and two globalDIC methods are theoretically analyzed atfirst.Subsequently,based on the same algorithmic details and parameters during analyses ofnumerical and real experiments,the performance of the different DIC approaches is fairly compared.Theoretical and experimental results reveal that local DIC outperforms its global counterpart in terms of both displacement results and computationalefficiency when element(subset)size is no less than 11 pixels.

©2016 The Author(s).Published by Elsevier Ltd on behalfof The Chinese Society of Theoreticaland Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

1.Introduction

Benefiting from rapid development of industrial camera,modern computer,and image processing technique,digital image correlation(DIC)[1-3],initially emerged in 1980s,has kept booming during lastthree decades due to its simplicity,practicality,and wide application range.In DIC analysis,image displacements(in pixels)are first determined by matching digital images of flat surface(2D-DIC)or curved surface(stereo-DIC)using certain image registration algorithm.Then,the physicaldisplacement can be further evaluated according to certain imaging model.Since strain estimation and identification of material parameters are generally performed on the basis of displacement fields,accurate displacement measurement is always a major focus in DIC algorithm.

Although plenty of DIC algorithms have been developed, subset-based DIC(local DIC)[4-21]and finite element-based DIC (FE-based global DIC)[22-35]are the two most commonly used ones.LocalDIC allocates separate reference subsetcentered ateach calculation point at first,then traces the corresponding deformed subset in target images using a local shape function.As such, local DIC processes a calculation point at a time independently without displacement continuity enforcement applied to the global displacement fields.Alternatively,global DIC usually discretizes the specified region of interest(ROI)into elements connected by nodes,and then traces allthese elements in the target image simultaneously to evaluate all the nodal displacements. In this sense,displacement continuity can be explicitly ensured between adjacent elements by the shared nodes.

In retrospect of the historical development of DIC technique, it is seen that subset-based local DIC emerged first and has been widely applied.Initially proposed to realize full-field displacement measurement in 1982[1],local DIC can only reach integer-pixelaccuracy.Motivated by improving both accuracy and efficiency,various localoptimization algorithms,such as gradientbased method[4,5],correlation coefficient curve-fitting method [6,7],Newton-Raphson(NR)algorithm[8-10],and quasi-Newton algorithm[11,12],were successively developed during the following 20 years.To unify the disagreement on algorithm selection,Pan et al.[13]experimentally demonstrated that NR algorithm outperforms other methods in terms of displacement accuracy and precision,which makes it become the standard DIC algorithm. Subsequently,to further satisfy the accuracy and efficiency requirement in diverse time-critical applications,researchers gradually focus on algorithm details and parameter selection,such as shape function[14,15],correlation criterion[16,17],interpolation scheme[18,19],and subset size[20].Recently,inspired by the inverse compositional matching algorithm widely adopted in computer vision,Pan et al.[21]proposed the inverse compositional Gauss-Newton(IC-GN)algorithm,which offers higher accuracy and efficiency than classic NR algorithm,and is highly recommended as a new standard algorithm.

At the beginning of the 21st century,in the meantime of rapid development of local DIC method,several researchers attempted to combine DIC with the finite element method(FEM).Bsplinebased[22],four-node FE-based[23,24],and eight-node FE-based global DIC approaches[25]were successively proposed to ensure global continuity of displacement field.To allow more complex cases during the analysis of fracture,bending and discrete geometry,various algorithmimprovements,such as extended DIC(X-DIC) [26,27],non-uniform rational B-spline(NURBS)[28],quasi-3D FE-DIC[29],and single-element X-DIC[30],were put forward. However,the inherent drawback of global DIC is the compromise between spatial resolution and displacement uncertainty. Specifically,higher spatial resolution requires denser mesh,resulting in larger displacement fluctuation(i.e.,displacement uncertainty or random error).As such,to enhance displacement precision in the case of high spatialresolution,a series of regularization strategies,such as temporalregularity[31],Tikhonov regularization[32],and proper generalized decomposition[33],were applied to global DIC.Alternatively,to balance the tradeoff between spatialresolution and displacement uncertainty,p-adaptive global DIC[34]and h-adaptive global DIC[35]were developed by adaptively selecting higher-order element and refining element, respectively.

Due to its outstanding advantages such as easy implementation, high accuracy,and high efficiency,local DIC has been applied in most commercial systems and practical applications up to now. Nevertheless,recent works[36]claim that global DIC may lead to better displacement results due to the displacement continuity constrain,thus posing an important issue of evaluating and comparing the performance of local and global DIC algorithms. Therefore,a detailed examination oftheir respective performances becomes attractive and pressing.Here,we summarize our recent research results on the performance evaluation of localand global DIC.In the following,the fundamental principles of local and global DIC are first briefly reviewed to ensure fair comparison. Then,the governing formulas of random errors associated with local DIC and two global DIC algorithms are derived.Finally,by using both numerical and real experiments,the measurement errors and computational efficiency of local DIC,four-node FE-based DIC(Q4-DIC),and eight-node FE-based DIC(Q8-DIC)are thoroughly compared.Experimental results demonstrate that local DIC outperforms global DIC in the case of relatively large element(subset)size and matched(or overmatched)shape function.

2.Basic principles and algorithmic details

To make the performance comparison fair enough,the same algorithm details including correlation criteria,subpixel registration algorithm,interpolation scheme,initial guess,and convergence condition employed in local and global DIC should be carefully defined.Though the basic principles of the two DIC techniques have been fully characterized in the literature[8-10, 23-25],the algorithmdetails in the two DICapproaches are briefly reviewed for clarity.

2.1.Basic principles

Both localand globalDICemploy certain matching algorithmto obtain initial displacement with integer-pixel accuracy,and then adopt specific subpixel registration algorithm(such as,nonlinear optimization algorithm or curve fitting algorithm)to further improve displacement accuracy.As illustrated in Fig.1,however,thetwo algorithms are essentially different in terms of describing the underlying deformation field.Based on the localapproximation to the kinematicalfields(including displacementand strain field),local DIC tracks the shape and position change of reference subset centered at each calculation point.By introducing continuous deformation hypothesis in solid mechanics,local continuity of the displacement field within each subset can be enforced,and hence can be characterized by specific shape function.In local DIC,adjacent subsets are analyzed independently without imposed continuity conditions a prior,thus resulting in separate or overlapping of deformed subsets.In contrast,global DIC is established on the basis ofglobaldescription of the kinematicalfield and widely-used FE framework.As such,global DIC tracks the position of all the nodes(i.e.,calculation points)simultaneously,thus being able to evaluate the entire displacement field at a time with the explicitly ensured displacement continuity among elements.

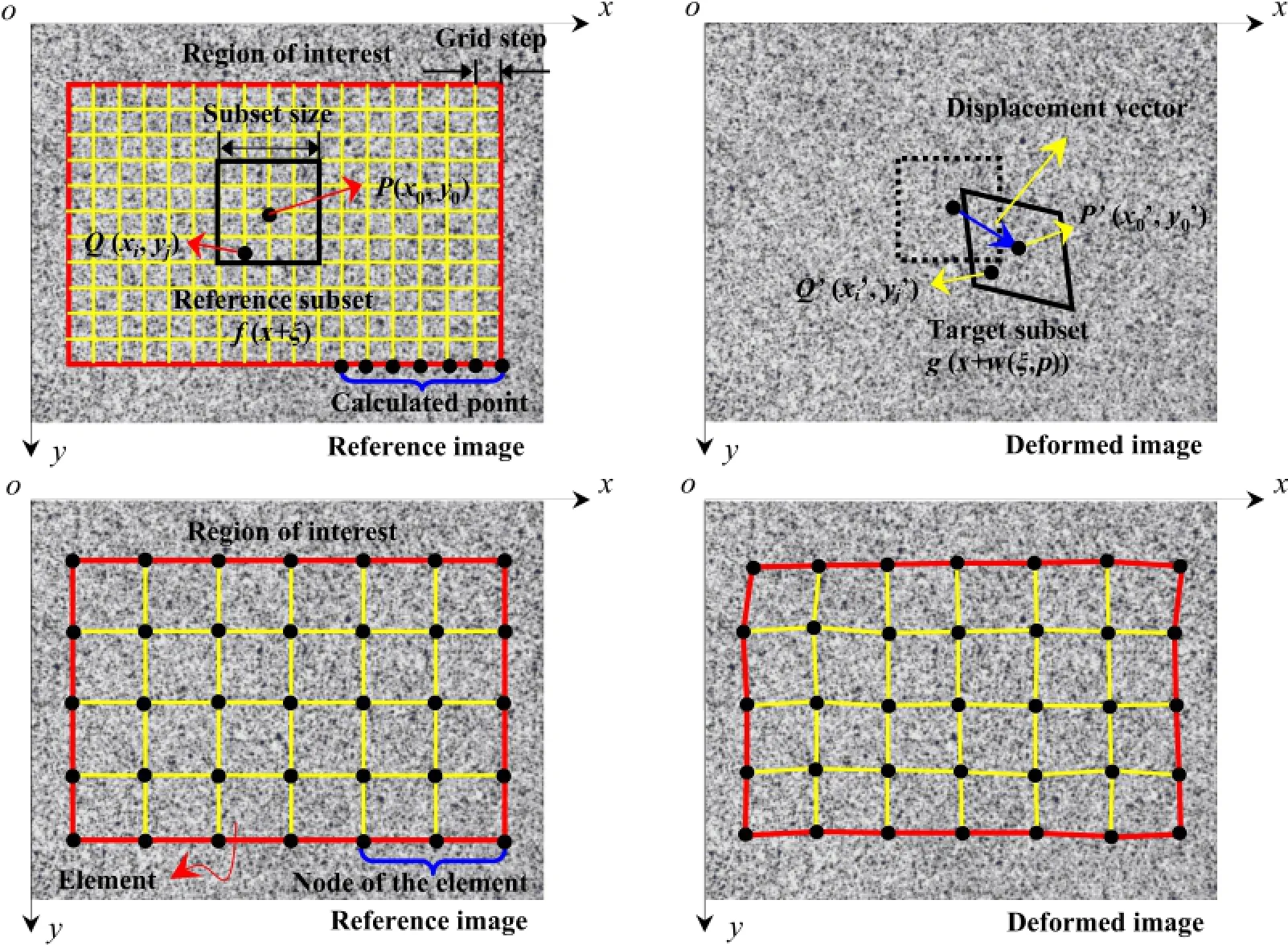
Fig.1.Displacement tracking strategy of local DIC(top)and global DIC(bottom).

2.2.Correlation criterion

During practical experiments,the deformed images captured from different perspectives or at different states may experience unavoidable changes in brightness and image contrast.To accommodate these possible intensity changes,local DIC generally employs a zero-mean normalized sum-of-square difference(ZNSSD) criterion[16,17]to assess intensity similarity

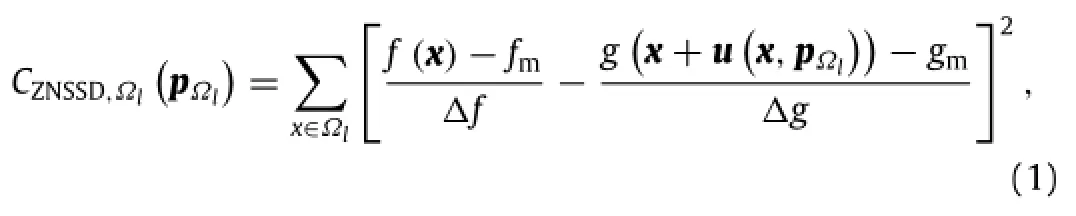
where f and g,respectively,represent reference and deformed subset;the gray levels at point x;the mean intensity values;the standard deviations of grayscalesis the reference subset;the shape function, specifically a first-order shape function in this work.

Likewise,to make the comparison fair,global DIC should adopt the ZNSSD criterion as similarity metric

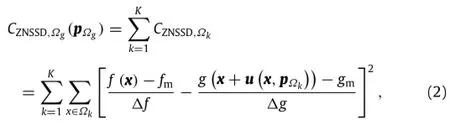
where f and g,respectively,denote reference and deformed element;is the entire computational region including K elements;the k th element;the shape function for k th element.Similar to the definition in FEM,the displacement of every pixel can be determined by the shape function and the nodal displacement within the element.Based on detailed literature survey,two primary global DIC approaches,i.e.,Q4-DIC[23,24]and Q8-DIC[25],are commonly employed.The former can approximate bilinear displacement field,while the latter can characterize quadratic displacement field due to its higher-order shape function.

2.3.Optimization algorithm

To obtain deformation components with subpixelaccuracy,the above defined ZNSSD function can be iteratively optimized using classic NR algorithm.For both local and global DIC approaches, each iteration can be expressed as

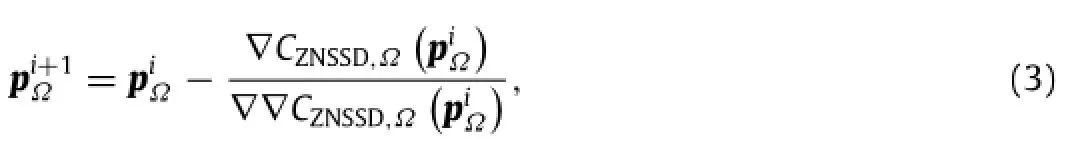
where i is the iteration number;for local DIC andfor global DIC.are the first-order and second-order gradients of the ZNSSD criterion,and the latter is also defined as the Hessian matrix.For a more detailed description, interested reader can refer to Refs.[8-10].

During the implementation of optimization algorithm,every integer-pixel in reference image is updated to subpixellocation in target image after each iteration.Therefore,specific interpolation method is required to offer the gray values and intensity gradients to NR algorithm.In this work,a bicubic interpolation approach combining with an interpolation coefficient look-up table[10,21] is adopted.Meanwhile,before DIC analysis,all the images are smoothed by Gaussian pre-filter technique with a 5 X 5-pixels window for the purpose of bias error reduction[37].Benefiting from this technique,the bias errors of the two DIC approaches are almost one order of magnitude less than standard deviation error (SDE).

2.4.Initial guess and convergence conditions

During practical implementation,NR algorithm necessities an enough accuracy initial guess to ensure correct convergence and an appropriate convergence condition to control convergence precision and iterative number.Here,the spatial-domain integerpixel searching scheme is employed to seek initial displacement for two DIC approaches,though more efficient strategies[38,39] have been developed.Besides,to follow the suggestion reported in Ref.[40],the convergence criterion defined in local DIC can be written as

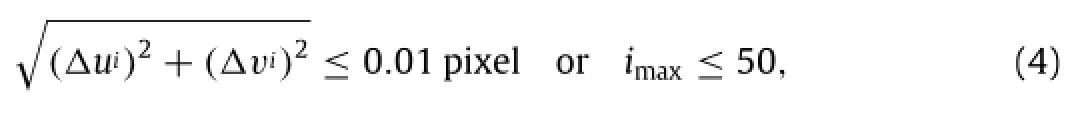
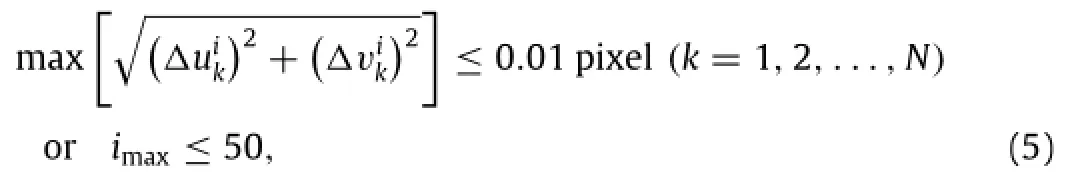
3.Theoretical analysis of random errors

Regarding three DIC methods,i.e.,local DIC,Q4-DIC,and Q8-DIC,mathematical derivation is carried out to uncover the governing formula of random errors.Three reasonable assumptions are made prior to the entire derivation.

(1)The bias errors induced by image noise and interpolation are negligibly small,since all the images are smoothed by a Gaussian pre-filter technique before DIC analysis,as recommended in the existing literature[37].

(2)The bias errors arising from mismatched shape functions are absent because the deformation model(i.e.,translation) employed in this work can be accurately characterized by the shape functions in the three DIC methods.

(3)The random errors due to imperfect interpolation are neglected,namely,the grayscales and intensity gradients at the same point before and after deformation are ideally equal [20,41].

Throughout the derivation,the random errors of the three DIC methods are theoretically analyzed in one-dimensionaltranslation case.First,let f(x)and g(x)represent the gray levels at point x in the images recorded before and after deformation,respectively. Then,σis the standard deviation of zero-mean white Gaussian noise added to the images.Finally,suppose that the measured displacement is u′=(u′,v′)and can be divided into the actual displacement u=(u,v)and the displacement error ue=(ue,ve). The SDEs due to the three DIC approaches are briefly denoted as follows.More details can be found in recent work[42].

3.1.Subset-based local DIC

As an objective function for similarity measure,the SSD criterion used in subset-based local DIC is defined as

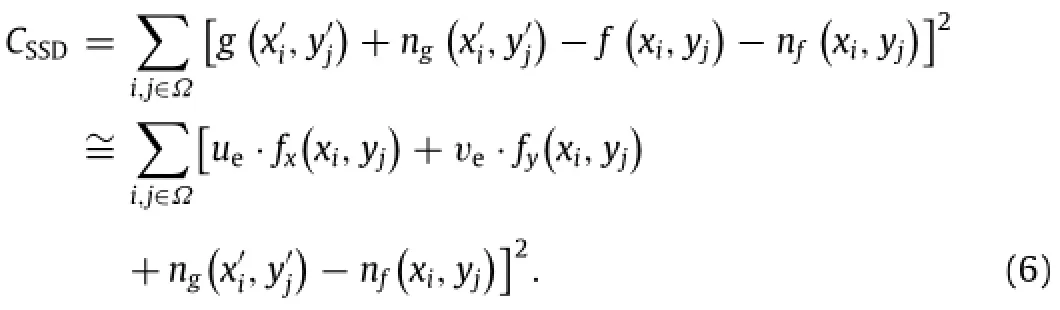
In the above formula,Ω is a single subset with a size of(K+pixels;are the intensity gradients of the reference image;are the intensities of noise involved in reference and deformed images.The standard deviation of the displacement error uein subset-based DIC can be derived by minimizing SSD function[20]

3.2.GlobalQ4-DIC

In the similar manner,the SSD criterion employed in global Q4-DIC is simplified as

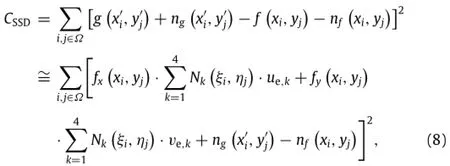
whereΩdenotes a single Q4 element with a size ofpixels. Similar with the parameter SSSIGdefined in localDIC,in the above equation is defined as sum of square of element intensity gradients(SSEIG).

To establish FE framework,an assembly matrix is always required to transform the nodal displacement of each Q4 element into the globalnode displacement matrix.Generally,supposed that the ROIis meshed into N X N Q4 elements,the SDE induced by global Q4-DIC can be denoted aswhere parameter P1is a variable related to parameter N,and their relationship can be established according to the global assembly matrix as depicted in Fig.2.

Table 1 Theoreticaland normalized SDEs of localand globalDIC methods.

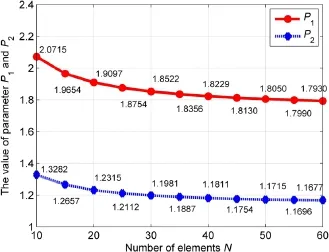
Fig.2.The diagram showing the parameter P1in Q4-DIC and the parameter P2in Q8-DIC varying with the number ofelements N.

3.3.Global Q8-DIC

Similar with global Q4-DIC,the final SDEs arising from Q8-DIC withoutassembly is written as

whereΩis a single Q8 element with a size of(2K+1)2pixels. It is worth mentioning that the Q8 element is twice the size of Q4 element to ensure same calculation points.Assume that the ROI is meshed by N X N Q8 elements,the general form of the SDEs associated with globalQ8-DIC can be expressed as

where P2is a variable relevant to the number of elements N.As depicted in Fig.2,the relationship between the parameter P2and the number of elements N can be established.

According to formulas derived above,the theoretical and normalized SDEs of the three DIC approaches are listed in Table 1. An observation reveals that local DICgives rise to the smallest SDEs in theory,while the SDEs induced by the two global DIC are more pronounced and their normalized SDEs with respect to local DIC are 1.8-2.2 and 1.2-1.6,respectively.

4.Experimental comparison by numerical tests

4.1.Numerical experiments

A series of rigid-body translation tests using numerically simulated speckle patterns were performed and analyzed by the local and global DIC methods to quantify the computational efficiency and measurement accuracy.During the experiments, five sets oftranslated images including Gaussian noise with diverse levels were generated.The first noise-free image set contains one reference and ten target images(800X800 pixels at 256 gray scale) with the pre-applied motions along x-direction ranging from 0 to 1 pixelat an increment of 0.1 pixels[18].Then,four sets ofrandom Gaussian noises with SDs ranging from 1 to 4 grayscales were added to the noise-free image set to simulate another four noisy counterparts.For a more detailed description,interested reader can refer to Ref.[43].

Subsequently,above-mentioned three DIC techniques were implemented to process all these images.Carefully selected calculation parameters were exhibited in Fig.3 to ensure the same calculation points and fair comparison.The calculation points (or element nodes)in reference image is defined as a uniformly distributed N X N square grid.In localDIC,the subset size was set as(K+1)2pixels and grid step was chosen as K pixels(K is even). Equally,an element size of(K+1)2pixels and(2K+1)2pixels for Q4-DIC and Q8-DIC were,respectively,applied as recommended in Ref.[25].The hardware configuration for the implementation of three DIC codes programmed by C++language were identical, i.e.,desktop computer with PentiumR○dual-core CPU E6600 and 3.06 GHz main frequency.

To estimate the statistics of the displacement errors,the measured displacements are compared with the actual ones. Generally,the displacement errors arising from DIC algorithms consistofsystematic error(or mean bias error(MBE))and random error(or SDE).However,due to the pre-filtering technique as mentioned above,the MBEs induced by allthe three DICalgorithms can be neglected.Accordingly,the SDEs arising from these DIC approaches almost equaltotalerrors defined as root-mean-squares error(RMSE),which can be expressed as

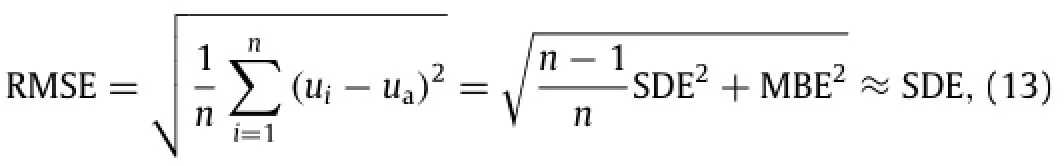
where uirepresents the estimated displacement of the i th calculation point,uadenotes the actualsubpixeldisplacement.

4.2.Comparison using image sets at various noise levels

Prior to the DIC analysis,Gaussian per-filter was applied to all the images to reduce noise with lower grayscale.The parameters N and K,dominating the calculation point distribution and subset (element)size,are selected as 16 and 40,respectively.Figure 4(a) exhibits the relationship between the RMSEs resulting from the three DIC methods and the applied subpixelmotions with respect to the fifth image set.It can be intuitively seen that(1)the RMSEs are almost unchanged with the varying subpixel motions;(2) the local DIC induces smaller RMSEs than the two global DICs, while Q8-DIC generates less RMSEs than Q4-DIC.Figure 3(b)shows the average RMSEs in the calculated displacements at different noise levels.An observation reveals that the RMSEs of all the three DICs almost linearly increase with the noise level,and local DIC offers smallest RMSEs in all cases,while Q8-DIC exhibits better accuracy than Q4-DIC.Figure 3(c)indicates the normalized experimental and theoretical RMSEs associated with two global

DICs with respect to that induced by local DIC at various noise levels.The comparison uncovers thatthe normalized experimental RMSEs arising from two global DICs almost remain unchanged at diverse noise levels,and agree well with the theoretical ratios predicted by the above governing formula.

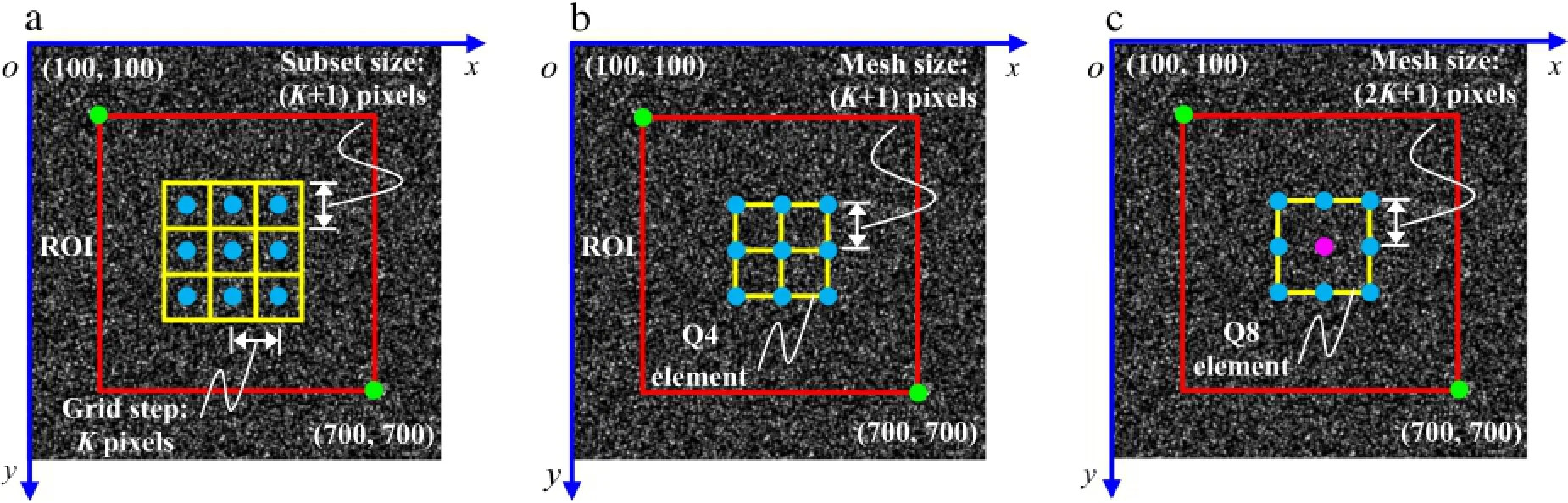
Fig.3.Algorithmic details employed in(a)local DIC;(b)Q4-DIC;(c)Q8-DIC.

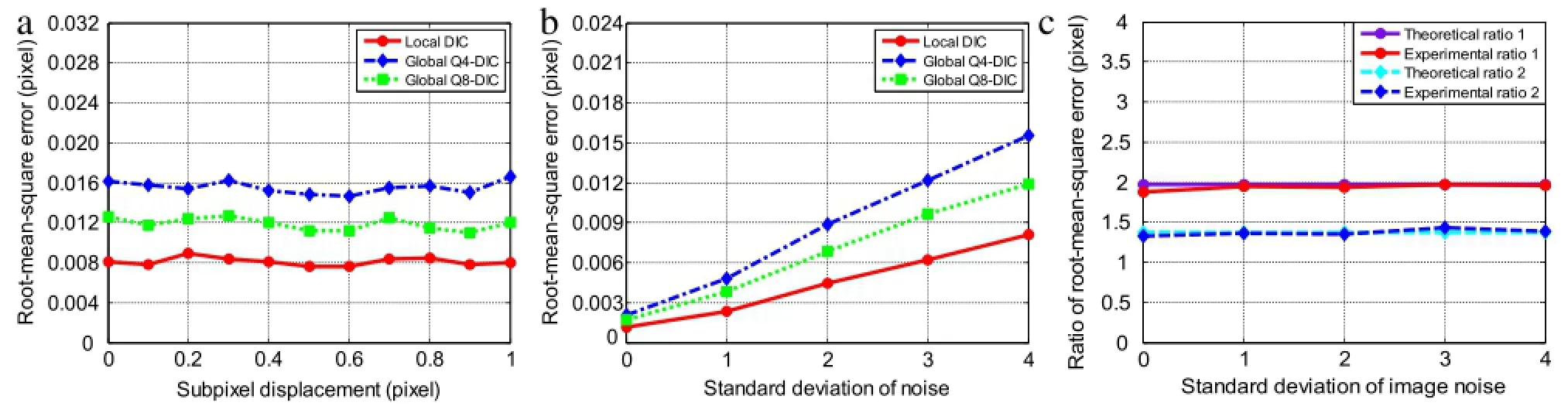
Fig.4.(a)The relationship between the RMSEs due to three DICmethods and subpixeldisplacements for the fifth image set(image noise with a SD of4).(b)The relationship between average RMSEs and the noise levels.(c)The normalized experimentaland theoretical RMSEs induced by two global DICs with respect to local DIC in the case of diverse noise levels.

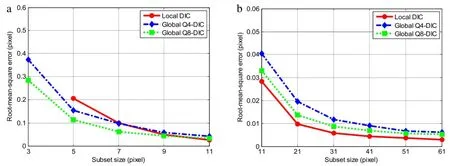
Fig.5.The RMSEs induced by three DICs using different element(subset)size:(a)smaller than 10 pixels;(b)larger than 10 pixels.

4.3.Comparison using various subset or element sizes

To further investigate their accuracy and precision,the third image set(image noise with an SD of 2)were processed by the three DIC methods with different subset(or element)sizes.Figure 5 depicts the average RMSEs due to the three DIC approaches with respectto the employed subset(or element)size.It should be pointed out that the total number of calculation points decreases with the increase ofelement(subset)size,which indicates the compromise between displacement uncertainly and spatialresolution.It can be clearly seen from Fig.5 that the average RMSEs decrease when element(subset)size increases since more pixels are included in single subset(element)and the effect of noise is suppressed.It can be also noted from Fig.5(b)that local DIC produces less RMSEs than two global DICs when using element(subset)size larger than 10 pixels.On the contrary,an opposite phenomenon can be detected as shown in Fig.5(a)when smaller element(subset)is adopted.As for two global DICs,Q8-DIC outperforms Q4-DIC in all cases.Although only typicalresults are illustrated here,allthese numerical experiments indicate the advantages of local DIC over global DIC. However,the latter stillhas its potentialmerit:globalQ8-DIC may be superior to local DIC when dealing with significantly heterogeneous deformation due to the data robustness in the case of using small element.

Table 2 The computationalefficiency ofthree DIC methods when dealing with the third translated image set(noise with an SD of2).

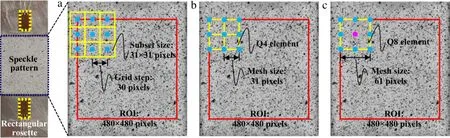
Fig.6.Calculation parameters employed in(a)local DIC,(b)Q4-DIC,and(c)Q8-DIC during the deformation measurement of the uniaxial tension images.

4.4.Comparison of computational efficiency

The calculating speed and average iteration number(AIN)of localand global DIC algorithms(subset or element size is selected as 41 X 41 pixels)during analyzing the first three image sets are exhibited in Table 2.It can be clearly seen that(1)as noise levels increase,the calculating speed of three DIC techniques decreases, and the corresponding average iteration number increases; (2)local DIC results in less average iteration number than global DIC due to better convergence performance,whereas Q8-DIC requires more AIN than Q4-DIC;(3)local DIC has obvious speed advantage over globalDIC in allcases,and globalQ8-DIC is superior to global Q4-DIC in terms of computing speeds.The efficiency advantage of local DIC over global DIC can be mainly attributed to the following three aspects:(1)compared with local DIC, global DIC requires more iteration number to satisfy the same convergence condition;(2)global DIC requires the transformation of displacement vector and''rigidity''matrix from the element scale to global(mesh)scale;(3)during the evaluation global displacement vector,a large sparse''rigidity''matrix should be solved in global DIC.

5.Experimental comparison by real experiments

To further examine their practical performance,real experimental images captured during uniaxial tensile test of a standard aluminum sample were analyzed.To eliminate the error induced by imperfect imaging,a bilateral telecentric lens was used to capture the speckle patterns on the surface of the specimen at a tensile load of 1.0 kN(reference image)and 8.5 kN(deformed image). Meanwhile,to detect the transversaland axialstrains of the sample during loading,two strain gages were pasted beside the speckle pattern.Figure 6 showsthe reference image cropped fromthe originally captured image(1280 X 1024 pixels at 256 grayscales).The red rectangles are the defined ROI including 17 X 17 calculation points,and the distance between adjacent calculation points is selected as 30 pixels.More details about element(subset)size can be seen in Fig.6.Then,globalplane fitting was performed with respect to the measured displacement fields to extract the normal strains,which is subsequently compared with the average strain results detected by the strain gages to quantify the strain errors of the three DIC methods.For more details,one can refer to Ref.[43].

Figure 7 exhibits the u and v displacement fields evaluated by localand two globalDIC techniques,and the inserted table lists the globally fitted value as wellas relative bias(the bias offitted values with respect to that detected by strain gages)ofstrain components and Poisson ratio along with the correlation coefficient of the global fitting.The displacement fields evaluated by local DIC are much smoother compared with that measured by global DIC. Moreover,two conclusions can be drawn with respect to global DIC:(1)the measured displacements along the boundary are much fluctuating than that in the center region due to lack ofcontinuity constraints during displacement analysis;(2)the fluctuation in displacement field detected by Q8-DIC is smaller compared with Q4-DIC since larger element size efficiently suppresses the detrimental effect of image noise.The inserted table reveals that (1)compared with global DIC,local DIC provides displacement field with larger correlation coefficients,thus resulting in smoother displacement field;(2)the strains and Poisson ratio evaluated by local DIC are closer to the actual results detected by strain gauges. Note that the correlation coefficient ofεyis closer to 1 than that ofεxbecause the larger deformation makes the influence of noise less along y direction than x direction.Although notdescribed here, the strain results of other tensile images captured in this test also demonstrate that local DIC offers better displacement and strain results.

6.Concluding remarks

In the development of DIC,both local and global DIC methods have been proposed and advocated for full-field displacement measurement.In this work,by carefully selecting the same algorithm details,the measurement accuracy and computational efficiency oflocalDIC and two global DICmethods were thoroughly compared through theoreticalerror derivation as wellas a series of numericaland realexperiments.Both the governing formulas and experimentalresults indicate the following:

(1)The local DIC offers better displacement precision than the two global DIC methods.However,it is worth mentioning that the differences in displacement measured by these DIC methodsare less than 0.02 pixels in numerical experiments;the average normalstrains evaluated by local DICseemslightly better than that by global DIC in realuniaxialtensile test.These minor differences during deformation measurement should not be overemphasized.

Fig.7.(Color online)The u(left)and v(right)displacement fields calculated by three DIC methods:localDIC(top),Q4-DIC(middle),and Q8-DIC(bottom).

(2)The local DIC exhibits higher efficiency than global DIC. Besides,a more robust and efficient IC-GN algorithm combining a reliability-guided displacement tracking(RGDT)strategy has been applied to subset-based local DIC recently[21],which indicates higher computational efficiency.

It should be mentioned here that local de-correlated regions may appear due to loss of local speckle patterns in dynamic experiments or significant fluctuation of local intensity during high-temperature tests.Under such circumstance,local DIC can robustly deal with the local de-correlated regions in the speckle pattern by using a RGDT strategy to separate these uncorrelated points and ensure the displacement tracking of other points uninfluenced,while the practicality of global DIC is questionable.

Although global DIC is proven inferior to localDIC in this work, the former indeed exhibits several irreplaceable merits in several specific respects listed as follows:

(1)Global DIC can directly establish connections between experimental results and numerical simulations by using the same FE basis with FEM analysis.It contributes to minimize the discretization error in DIC compared with simulated results and conversely optimize the numericalmodel in FEM analysis.

(2)Global DIC can keep displacement robustness even using element size with several pixels thanks to the global continuity constraint,while the subset size used in local DIC should be large enough to ensure accurate matching.As such,the potentialofusing small element makes global DIC more competent in the case of greatly heterogeneous deformation.

Acknowledgments

This work is supported by the Science Fund of State Key Laboratory of Automotive Safety and Energy(KF16162).

[1]W.H.Peters,W.F.Ranson,Digital imaging techniques in experimental stress analysis,Opt.Eng.21(1982)213427.

[2]B.Pan,K.Qian,H.Xie,etal.,Two-dimensionaldigitalimage correlation forinplane displacement and strain measurement:a review,Meas.Sci.Technol.20 (2009)062001.

[3]J.J.Orteu,3-D computer vision in experimentalmechanics,Opt.Laser Eng.47 (2009)282-291.

[4]C.Q.Davis,D.M.Freeman,Statistics of subpixel registration algorithms based on spatiotemporal gradients or block matching,Opt.Eng.37(1998) 1290-1298.

[5]J.Zhang,G.Jin,S.Ma,et al.,Application ofan improved subpixelregistration algorithm on digitalspeckle correlation measurement,Opt.Laser Technol.35 (2003)533-542.

[6]D.J.Chen,F.P.Chiang,Y.S.Tan,et al.,Digital speckle-displacement measurement using a complex spectrum method,Appl.Opt.32(1993)1839-1849.

[7]P.C.Hung,A.S.Voloshin,In-plane strain measurement by digital image correlation,J.Braz.Soc.Mech.Sci.25(2003)215-221.

[8]H.A.Bruck,S.R.McNeill,M.A.Sutton,et al.,Digital image correlation using newton-raphson method of partial differential correction,Exp.Mech.29 (1989)261-267.

[9]G.Vendroux,W.G.Knauss,Submicron deformation field measurements:Part 2.improved digitalimage correlation,Exp.Mech.38(1998)86-92.

[10]B.Pan,K.Li,A fast digital image correlation method for deformation measurement,Opt.Laser Eng.49(2011)841-847.

[11]P.Zhou,K.E.Goodson,Subpixel displacement and deformation gradient measurement using digital image/speckle correlation(DISC),Opt.Eng.40 (2001)1613-1620.

[12]H.Wang,Y.Kang,Improved digital speckle correlation method and its application in fracture analysis ofmetallic foil,Opt.Eng.41(2002)2793-2798.

[13]B.Pan,H.Xie,B.Q.Xu,et al.,Performance of sub-pixel registration algorithms in digitalimage correlation,Meas.Sci.Technol.17(2006)1615.

[14]H.W.Schreier,M.A.Sutton,Systematic errors in digitalimage correlation due to undermatched subset shape functions,Exp.Mech.42(2002)303-310.

[15]L.Yu,B.Pan,The errors in digitalimage correlation due to overmatched shape functions,Meas.Sci.Technol.26(2015)045202.

[16]W.Tong,An evaluation of digitalimage correlation criteria for strain mapping applications,Strain 41(2005)167-175.

[17]B.Pan,H.Xie,Z.Wang,Equivalence of digital image correlation criteria for pattern matching,Appl.Opt.49(2010)5501-5509.

[18]H.W.Schreier,J.R.Braasch,M.A.Sutton,Systematic errors in digital image correlation caused by intensity interpolation,Opt.Eng.39(2000)2915-2921.

[19]A.Baldi,F.Bertolino,Experimental analysis of the errors due to polynomial interpolation in digitalimage correlation,Strain 51(2015)248-263.

[20]B.Pan,H.Xie,Z.Wang,et al.,Study on subset size selection in digital image correlation for speckle patterns,Opt.Express 16(2008)7037-7048.

[21]B.Pan,K.Li,W.Tong,Fast,robust and accurate digitalimage correlation calculation withoutredundantcomputations,Exp.Mech.53(2013)1277-1289.

[22]P.Cheng,M.A.Sutton,H.W.Schreier,et al.,Full-field speckle pattern image correlation with b-spline deformation function,Exp.Mech.42(2002) 344-352.

[23]Y.Sun,J.H.L.Pang,C.K.Wong,et al.,Finite element formulation for a digital image correlation method,Appl.Opt.44(2005)7357-7363.

[24]G.Besnard,F.Hild,S.Roux,Finite-element displacement fields analysis from digital images:application to Portevin-Le Châtelier bands,Exp.Mech.46 (2006)789-803.

[25]S.Ma,Z.Zhao,X.Wang,Mesh-based digital image correlation method using higher order isoparametric elements,J.Strain Anal.Eng.Des.47(2012) 163-175.

[26]J.Réthoré,S.Roux,F.Hild,Frompicturesto extended finite elements:extended digitalimage correlation(x-dic),C.R.Mec.335(2007)131-137.

[27]J.Réthoré,F.Hild,S.Roux,Extended digitalimage correlation with crack shape optimization,Internat.J.Numer.Methods Engrg.73(2008)248-272.

[28]J.Réthoré,T.Elguedj,P.Simon,et al.,On the use of nurbs functions for displacement derivatives measurement by digital image correlation,Exp. Mech.50(2010)1099-1116.

[29]J.Van Beeck,J.Neggers,P.J.G.Schreurs,et al.,Quantification of threedimensional surface deformation using globaldigitalimage correlation,Exp. Mech.54(2014)557-570.

[30]J.Chen,X.Zhang,R.Wang,Microdeformation measurement via singleelement extended digitalimage correlation,J.Strain Anal.Eng.Des.46(2011) 327-336.

[31]G.Besnard,H.Leclerc,F.Hild,et al.,Analysis of image series through global digitalimage correlation,J.Strain Anal.Eng.Des.47(2012)214-228.

[32]R.Yang,A regularized finite-element digital image correlation for irregular displacementfield,Opt.Laser Eng.56(2014)67-73.

[33]J.C.Passieux,J.N Périé,High resolution digitalimage correlation using proper generalized decomposition:PGD-DIC,Internat.J.Numer.Methods Engrg.92 (2012)531-550.

[34]X.Wang,S.P.Ma,Mesh-based digital image correlation method using nonuniform elements for measuring displacementfields with high gradient,Exp. Mech.54(2014)1545-1554.

[35]L.Wittevrongel,P.Lava,S.V.Lomov,et al.,A self adaptive global digital image correlation algorithm,Exp.Mech.55(2015)361-378.

[36]F.Hild,S.Roux,Comparison of local and global approaches to digital image correlation,Exp.Mech.52(2012)1503-1519.

[37]B.Pan,Bias error reduction of digital image correlation using gaussian prefiltering,Opt.Laser Eng.51(2013)1161-1167.

[38]Z.F.Zhang,Y.L.Kang,H.W.Wang,et al.,A novelcoarse-fine search scheme for digitalimage correlation method,Measurement 39(2006)710-718.

[39]B.Pan,Reliability-guided digital image correlation for image deformation measurement,Appl.Opt.48(2009)1535-1542.

[40]B.Pan,An evaluation ofconvergence criteria fordigitalimage correlation using inverse compositionalgauss-newton algorithm,Strain 50(2014)48-56.

[41]Y.Q.Wang,M.A.Sutton,H.A.Bruch,et al.,Quantitative error assessment in pattern matching:effects of intensity pattern noise,interpolation, strain and image contrast on motion measurement,Strain 45(2009) 160-178.

[42]B.Pan,B.Wang,G.Lubineau,Comparison ofsubset-based localand FE-based globaldigitalimage correlation:theoreticalerroranalysis and validation,Opt. Laser Eng.82(2016)148-158.

[43]B.Pan,B.Wang,G.Lubineau,et al.,Comparison of subset-based local and finite element-based global digital image correlation,Exp.Mech.55(2015) 887-901.

∗Corresponding author at:Institute of Solid Mechanics,Beihang University,Beijing 100191,China.

E-mail address:panb@buaa.edu.cn(B.Pan).

http://dx.doi.org/10.1016/j.taml.2016.08.003

2095-0349/©2016 The Author(s).Published by Elsevier Ltd on behalfof The Chinese Society of Theoreticaland Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*This article belongs to the Solid Mechanics