Magnetic induction strength on surface of a ferro-medium circular cylinder

Ming JinDepartment of Mechanics,SchoolofCivilEngineering,Beijing Jiaotong University,Beijing 100044,China

Letter

Magnetic induction strength on surface of a ferro-medium circular cylinder

Ming Jin
Department of Mechanics,SchoolofCivilEngineering,Beijing Jiaotong University,Beijing 100044,China

H I G H L I G H T S

.An analyticalintegral expression of relation between magnetic flux leakage(MFL)and magnetization of a ferro-medium circular cylinder is found.

.Magnetization of material can be predicted by the MFL on surface the circular cylinder.

A R T I C L E I N F O

Article history:

Received 20 May 2016

Received in revised form

5 August 2016

Accepted 15 August 2016

Available online 24 August2016

Cylinder Magnetization Stress Biot-Savart law

Based on the Ampere molecular current hypothesis and the Biot-Savart law,a magnetic model on the metal magnetic memory(MMM)testing of a specimen is proposed.Relation between magnetic flux leakage(MFL)and magnetization of a ferro-medium circular cylinder is set up.We can predict magnetization ofmaterialaccording to the MFL on surface ofthe circular cylinder.

©2016 The Author.Published by Elsevier Ltd on behalfof The Chinese Society of Theoreticaland Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

Metal magnetic memory(MMM)method is one of nondestructive tests on metal specimens.Many experiments showed that stresses have some effects on magnetic memory signal on surface of a metal specimen,i.e.,magnetic flux leakage(MFL). Wilson et al.[1,2]used a three axis magneto-resistive magnetic field sensor to measure the residual magnetic fields parallel to the applied stress and the material surface and perpendicular to the materialsurface generated by the magneto-mechanicaleffect without the application ofan externalfield.Stupakov et al.[3]presented a magnetic investigation of structure degradation of lowcarbon steel due to plastic tensile strain.Li et al.[4]gained the magnetic memory signal data in fatigue experiments to 16MnR base metal specimens.Dong et al.[5,6]showed that the normal component of magnetic memory signals depends on the applied stress.Shi et al.[7]showed that normal component of scattering magnetic field of 18CrNiA steel in static tension is linear.Li and Xu[8]measured surface magnetization on 1045 and A3 steelsamples uniaxially deformed to differing magnitudes ofplastic strain. Experiments of Roskosz and Bieniek[9,10]show that magnetization depends on type of material,strength of magnetic field,magnetic history,strain,and temperature.Leng et al.[11]explored magnetic memory signals of mild steel under uniaxial tensile stresses approaching and exceeding the macroscopic elastic limit and after unloading.A review on this issue in detail can be found in the paper of Wang et al.[12].

However relation between stress and magnetic memory signal on surface of a metal specimen is not very clear theoretically now.One ofthese problems is the relation between magnetization in material and the MFL on surface of a specimen.The Ampere molecular current hypothesis is a hypothesis on origin of magnetization in modern physics.Based on the Ampere molecular current hypothesis,magnetism in medium is caused by internal molecular current.The MFL on surface of material is caused by many internalmolecular currents in the ferro-medium.Therefore the MFL on surface of materialshould be quantitatively dependent on strength of the molecular currents in the ferro-medium.In this paper,based on the Ampere molecular current hypothesis,a theoreticalmodelis proposed to investigate the relation between magnetization in material and the MFL on surface of a circular cylinder specimen.

This paper presents the Biot-Savart law,the theoretical model of a circular cylinder,numerical results of normal magnetic induction strength on and over surface of a circular cylinder.

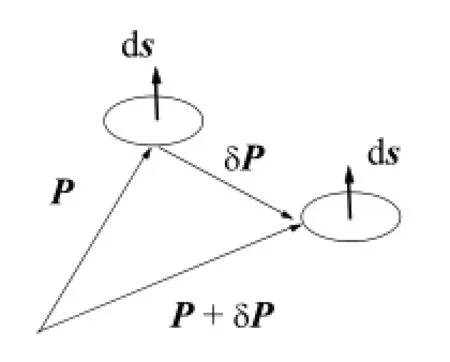
Fig.1.Solid angle.

Fig.2.Magnetic induction strength B by the smallelement with current circle d I.

Fig.3.A circular cylinder offerro-medium.

A solid angle of an area element d s to the point C in Fig.1 is defined as

where P is position vector of the area element d s,|P|is length of the vector P,and symbol''.''is the scalar product oftwo vectors.In Eq.(1),we have gradient of the solid angle with respect to P

In Fig.2,based on the Biot-Savart law,contribution of the magnetic induction strength of the small element with a current circle d I to the point C is

whereµdenotes magnetic conductivity ratio.

Figure 3 is a circular cylinder of ferro-medium.xyz and rθz are the Cartesian coordinates and the circular cylindricalcoordinates with the same origin,respectively.i,j,k are the unit vectors along axis ofthe Cartesian coordinates xyz.A(r,θ,z)and C(xc,0,zc)are an inner pointand an outpointofthe circular cylinder,respectively. Vector CA in Fig.3 is

Based on the Ampere molecular current hypothesis,the magnetization of ferro-medium is caused by many current circles in the ferro-medium.

We suppose that there is a current circle d I around the point A on surface ofthe differentialelement as shown in Fig.4,where

Fig.4.A current circle d I around point A.

and where M is the magnetization or increase ofthe magnetization at the point A.For example,increase of the magnetization may be caused by stress or deformation,in elastic or in plastic,in the circular cylinder.The area element d s in Fig.4 is

From Eqs.(4),(6),we have

Substituting Eqs.(4),(6),(7)into Eq.(2),we have the gradient ofthe solid angle ofd s to point C in Fig.3,i.e.,

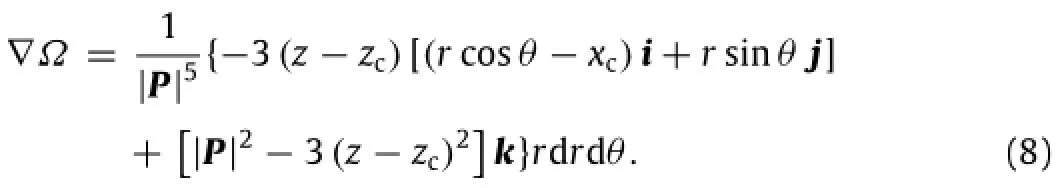
Substituting Eqs.(5),(8)into Eq.(3),we have the contribution of the magnetic induction strength of the differential element in Fig.4 to the point C in Fig.3,i.e.,

In Eq.(9),component of the magnetic induction strength normal to surface of the circular cylinder,i.e.,component of d B in direction of x,is

Suppose the magnetization M distributes uniformly in the circular cylinder,by integrating Eq.(10),we have the component ofthe magnetic induction strength normalto surface ofthe circular cylinder at the point C in Fig.3,i.e.the normal component of MFL on and over surface of the circular cylinder

and(see Eq.(13)in Box I)where

Because g in Eq.(13)is an odd function with respect toin Eq.(12)is an odd function with respect to

Numericalresults ofintegral(Eq.(12))are shown in Figs.5-8.

In Eqs.(11),(12),we know that tangent ofcurve is proportionalto the magnetization M ofmaterial.For example,tangent in Eq.(11)at

Box I.

Fig.5.When

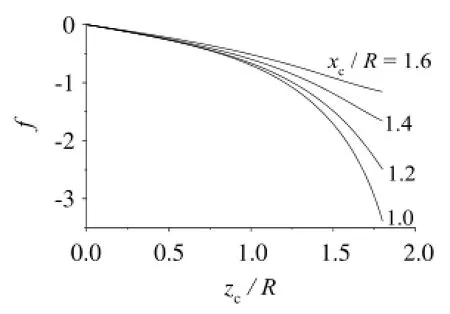
Fig.6.When

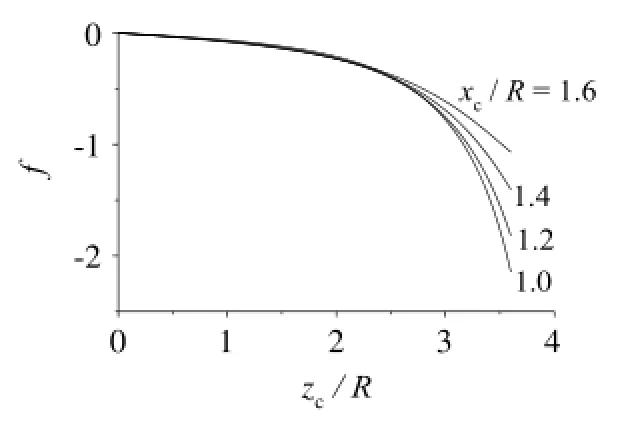
Fig.7.When

Fig.8.When

where

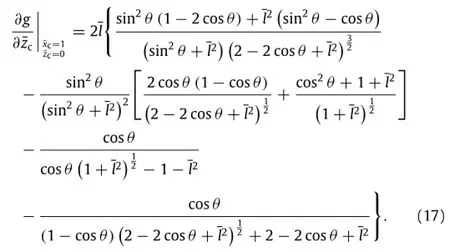
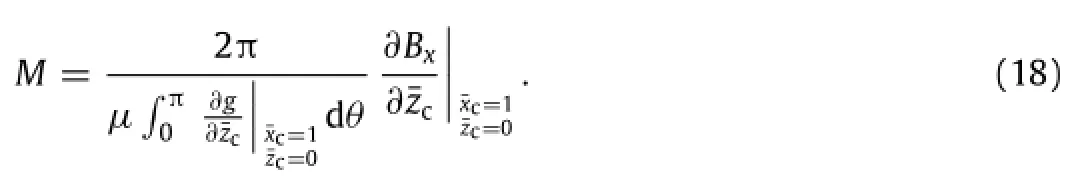
Based on the Ampere molecular current hypothesis and the Biot-Savart law,a magnetic modelon MMMtesting ofthe circular cylinder is proposed.By this model,the magnetization or increase of the magnetization in ferro-medium of a circular cylinder can be calculated by the MFL curve on surface of material.

For a solid circular cylinder specimen in simple axial tension or compression,increase of the magnetization may be dependent on increase of stress or strain,and state variables,such as stress,strain,elasticity or plasticity,loading or unloading,static loading or dynamical loading,environmental magnetic field and so on.Increase of stress or strain,and these state variables can be detected directly in experiment,while increase of the magnetization can be got indirectly in experiment,for example, by Eq.(18).Therefore,the model above gives a possible method to investigate the magneto-mechanical effect in a solid circular cylinder specimen in axialsimple tension or compression.

Acknowledgment

The project was supported by the Specialized Research Fund for the Doctoral Program of Higher Education of China (20120009110019).

[1]J.Wilson,G.Y.Tian,S.Barrans,Residual magnetic field sensing for stress measurementand defectdetection,in:ECNDT 2006-We.4.2.1,2006.

[2]J.Wilson,G.Y.Tian,S.Barrans,Residual magnetic field sensing for stress measurement,Sensors Actuators A 135(2007)381-387.

[3]O.Stupakov,J.Pal'a,I.Tomáš,et al.,Investigation of magnetic response to plastic deformation of low-carbon steel,Mater.Sci.Eng.A 462(2007) 351-354.

[4]J.M.Li,Y.L.Zhang,G.T.Shen,Study on the character of metal magnetic memory signalin the course ofhigh-cycle fatigue experimentfor 16MnRsteel, in:17th World Conference on Nondestructive Testing,Shanghai,China,2008, pp.25-28.

[5]L.H.Dong,B.S.Xu,S.Y.Dong,et al.,Variation of stress-induced magnetic signals during tensile testing of ferromagnetic steels,NDT&E Int.41(2008) 184-189.

[6]L.H.Dong,B.S.Xu,S.Y.Dong,etal.,Stress dependence ofthe spontaneous stray field signals of ferromagnetic steel,NDT&E Int.42(2009)323-327.

[7]C.L.Shi,S.Y.Dong,B.S.Xu,et al.,Metal magnetic memory effect caused by static tension load in a case-hardened steel,J.Magn.Magn.Mater.322(2010) 413-416.

[8]J.W.Li,M.Q.Xu,Influence ofuniaxialplastic deformation on surface magnetic field in steel,Meccanica 47(2012)135-139.

[9]M.Roskosz,M.Bieniek,Evaluation of residual stress in ferromagnetic steels based on residualmagnetic field measurements,NDT&E Int.45(2012)55-62.

[10]M.Roskosz,M.Bieniek,Analysis of the universality of the residual stress evaluation method based on residual magnetic field measurements,NDT&E Int.54(2013)63-68.

[11]J.C.Leng,Y.Liu,G.Q.Zhou,et al.,Metalmagnetic memory signal response to plastic deformation of low carbon steel,NDT&E Int.55(2013)42-46.

[12]Z.D.Wang,Y.Gu,Y.S.Wang,A review of three magnetic NDT technologies, J.Magn.Magn.Mater.324(2012)382-388.

E-mail address:jinmingjinming@hotmail.com.

http://dx.doi.org/10.1016/j.taml.2016.08.010

2095-0349/©2016 The Author.Published by Elsevier Ltd on behalfof The Chinese Society of Theoreticaland Applied Mechanics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*This article belongs to the Solid Mechanics