无线传感器网络的系统化自适应建模*

钟杰卓 杜文才 吴 慰

(海南大学信息科学技术学院，海口， 570228)



无线传感器网络的系统化自适应建模*

钟杰卓 杜文才 吴 慰

(海南大学信息科学技术学院，海口， 570228)

无线传感器网络的系统能耗制约着全网络的综合应用能力，其中节点有限的能量从根本上影响着传感器网络效能。针对无线传感器网络的全局能耗问题，提出了基于径向基函数神经网络以及状态空间表达的系统化建模方法。考虑到无线传感器网络的拓扑结构与分级关系, 采用径向基函数神经网络自适应实时规划系统。鉴于各传感器节点对数据的不同处理方式与能耗密切相关, 对全系统能耗建立系统化矩阵模型。仿真分析表明该模型可根据实际应用背景调整设置完成全局优化。

无线传感器网络； 径向基函数神经网络； 控制理论； 动态优化

引 言

在大规模集群计算中，能源维护成本极大，这与集群中的成员在线却无法合理利用密切相关。类似地,在无线传感器网络系统中也存在能源利用与数据计算的优化问题。更为重要的是,源感知节点和感知数据具有“生物酶”特性,亦即高耗能将导致失活并退出系统,从而引起系统重构。鉴于此,文献[1]提出了采用自适应控制策略重新配置移动无线传感器网络(Mobile wireless sensor networks,MWSN)方案来实现能耗相关的及时准确移动与多目标跟踪(Mobile multi-target tracking,MMTT),采用控制论从源节点的启动与退出策略出发来捕获数据,这类实时动态方法,对于未知的动态系统(如单节点受到大扰动产生突变等)缺乏必要的先验知识,需要额外的处理。Marcin Szczodrak等提出了动态地重新配置无线传感器网络的框架[2],采用预置的上层系统网络协议与对应的采样方法为应用事件触发WSN的重置,这是一种预置规划方法。国内外对于WSN的能耗与数据融合也做了很多有价值的研究[3-8]。无论是从系统物理结构层控制还是数据传输层面,此类WSN研究都有其相应的实际应用背景。如何让一个无线传感器网络模型既能结构化、整体化的可控表达,又具备较强的适应未知的动态能力,这是本文的研究重点。

1 相关理论

1.1 无线传感器网络信号流程架构

无线传感器网络的系统能量消耗主要集中在数据的发送、接收以及空闲状态,是大量的静止或移动的传感器以自组织和多跳的方式构成的无线网络,协作地探测、处理和传输网络覆盖区域内感知对象的检测信息,并上报处理[9]。由于电源能量有限,所以必须减少网络中不必要的能耗,合理的设置信号采集和处理方式,最大限度地融合信息并提交给上层管理系统。

1.2 系统的状态空间表达

系统由一组独立的状态矢量xT(t)=[x1(t),x2(t),…，xn(t)]构成的一阶微分方程组作为状态方程,如果明确了系统的输入u和输出y,则可以确定系统的输出方程。[10]状态方程和输出方程一并称为状态空间表达式,用矢量矩阵表示为

(1)

式中：xT=[x1,x2,…,xn],A为n阶系统矩阵,uT=[u1,u2,…,ur] 为r维输入矢量,yT=[y1,y2,…,ym] 为m维输出矢量。一个开环系统的自适应能力是有限的,系统设计往往采取实时负反馈闭环设计[11]。因此,有必要从管理单元引出反馈信号并加载到底层传感器单元,适当地调节节点的加入、切除与采样效率,调整系统输入,实时动态规划网络使得能耗与输出最优。

1.3 径向基函数神经网络

由于系统状态一致有界，且状态轨迹是周期性轨迹或者更一般的回归轨迹[12]，这里系统采样数据是离散化的。运用径向基函数神经网络对其进行逼近建模，并将学习到的知识存储到神经网络的权值中，以此用于动态环境下的控制。径向基函数神经网络(Radial basis function neural networks,RBFNN)由于其非线性化结构、并行分布式结构、克服局部极小值以及自我学习与适应能力等优点使得其应用不断扩大。

典型三层结构模式与WSN有着极强的内在联系与计算相似性。输入层类似于传感器源节点,用于捕获信号; 隐含层则将捕获的数据映射到一个相对高维度的空间,完成权值运算后，降低维度输出;网络的输出层类似于汇聚单元,输出数据到WSN系统的上层管理单元,用于下一步管理与分析。隐层空间的维数提高,网络的逼近能力越强,但因此带来的计算复杂度也会相应提高。

2 无线传感器网络模型

2.1 数据融合模型

按照实际情况,先分析位于同一块毗连区域中的节点数据。假设在一个周期t内某个节点xi采样n类不同测度的数据,得到

(2)

式中：α表示采集强度系数，α=0时不采集，α=1时采集。一共有k个传感器节点,则采集到的原始值矩阵记为

(3)

对于同一个节点,连续周期内采样值之间的欧几里得距离是有限常数，有

(4)

式中：Xi(t1)，Xi(t2)分别表示单个节点在连续周期t1，t2内测得的不同类型的数据列向量, M为欧几里得距离的上限值,且是一个有界数值。传感器节点在连续周期内采集到的数据之间差距不大,所以将每次采样的数据都发送给上层管理系统会造成浪费资源,因此对于同类数据信号的采集与处理就显得尤为重要。

对于分布在同一个划分区域内的不同节点测定的同类信号,在持续时间激励下,测定值如果产生了较大变化,那么认为它是优先级影响变量并需要对其优先处理,因此定义误差影响为

(5)

式中：xsum-k表示所有节点在连续周期t1，t2内测得的同类信号的数据,e(xsum-k)为该信号的总体误差。

2.2 能耗函数模型

感知层采集数据并计算数值的能耗函数取[13]

(6)

式中：i表示单个传感器,t表示时序，α表示采集强度系数,α=0时不采集，α=1时采集; Es为单位采集能耗值; β表示计算强度系数，β∈[0,1]; Ec为单位计算能耗值。数据发送的能耗函数采用如下形式

(7)

式中：i表示单个源传感器节点,l表示发送数据的比特数,d表示发送到汇聚节点的距离，d0表示源节点到汇聚节点的临界距离常数,Esnd为单位发送数据能耗, εfs·d2为自由空间模型，εamp·d4为多径衰落信道模型,用于表示功放的耗能。数据接收的能耗函数采用如下形式

(8)

式中：j表示单个汇聚节点,l表示发送数据的比特数。系统空闲、待机休眠状态能耗设为恒值参数。

3 无线传感器网络的系统化建模

对于一个已定义的WSN系统F,从源节点到处理终端产生了时态序列数据Y=[y1,y2,…, yk],未知的系统动态为p,目标是建立节省全网络能源并且具备较强适应力的全系统状态空间表达控制模式。系统参数设定: 对于一个无线传感器网络系统,传感器S数目为k,簇G的数目为r,设计如下的控制系统(图1)。

假设1 同一个簇中的节点采样同一类数据,且这些数据构成一个输出控制,在一个采样周期中不能全部被关闭,即

(9)

式中α1,2,…,i为一个簇中的节点采集强度系数。

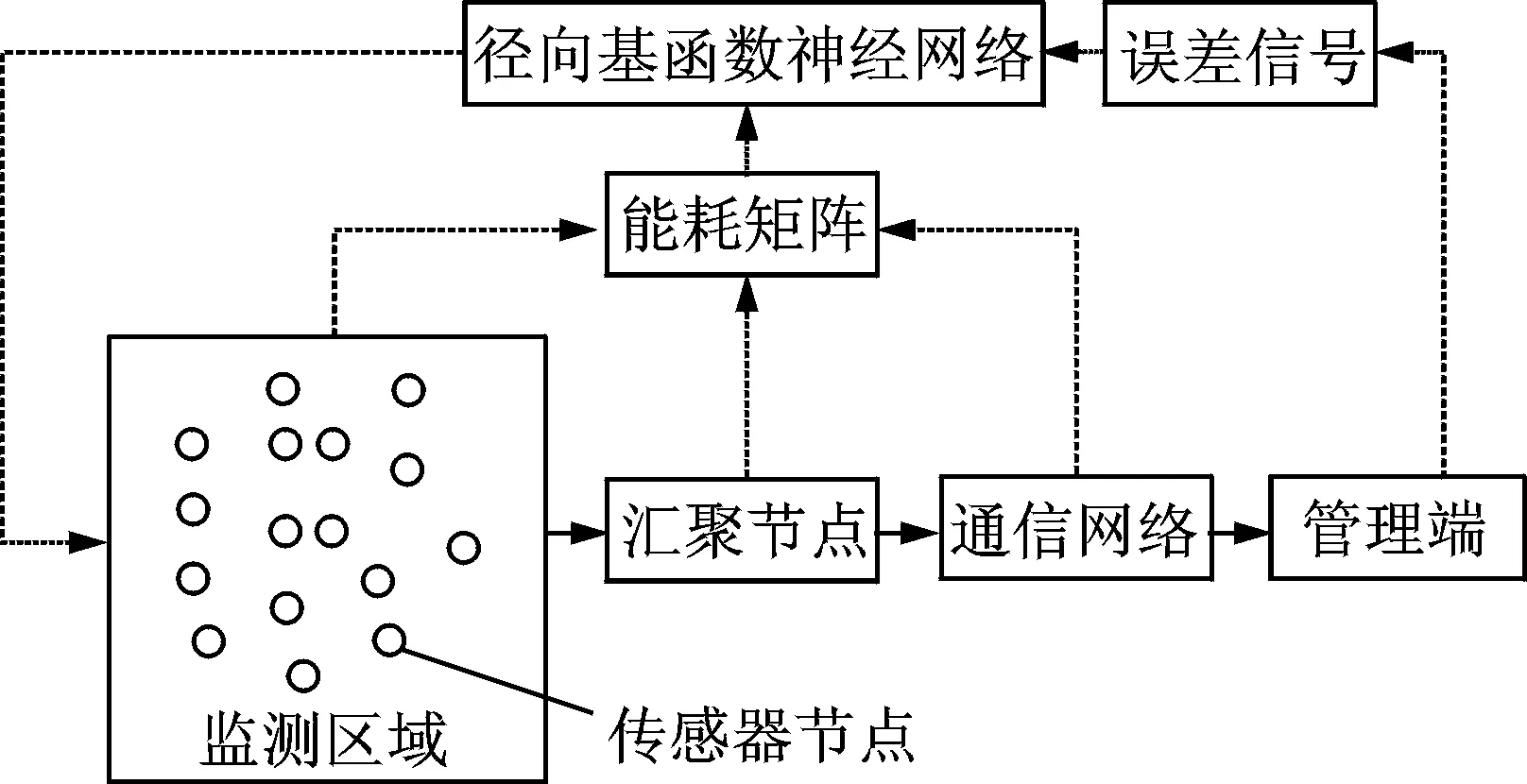
图1 无线传感器网络控制系统模型Fig.1 Network control system of wireless sensor networks

设簇Gi区域内分布着传感器节点a(i,1),a(i,2),…,a(i,k1),每个节点监测数据为xi,各节点的输入权值为wi,节点的位置和标识信息是确定的,且节点结构相同,汇聚节点输出y。

输入的采集数据向量经过隐含层神经元映射,融合得到的数据为

(10)

输入向量是一个有界紧集,Si(x)是径向基函数,通常选择高斯基函数作为基函数,表达形式为

(11)

其中ci∈Ωx (i=1,2,3,…m)为网络的中心,ηi为学习速率。隐含层向输出层输出数据为

(12)

式中bj是偏置信号,使用网络的输出作为融合后的数据作为发送处理数据。

可以看出,降低网络损耗的关键集中于采样数据的处理以及发送。因此建立能耗矩阵,在一次数据采集、处理和发送流程中,根据式(6～8)表达,设每一个行向量为每一个簇的总能耗,依次包括: 每个感知节点接收及发送数据的能耗、神经网络接收每个数据能耗、神经网络计算数据能耗、神经网络发送数据能耗和系统自身损耗，则系统能耗为

(13)

从中提取适当变量加入到神经网络权值的训练学习,提取的方式根据实际应用背景的不同而相异。设计提取规则后得到的传播信号为

(14)

其中eE为提取到的数值信号,Г为提取规则，该误差信号参与调整神经网络的权值,是网络传播的误差信号的一部分。另一部分的网络调整信号为系统的实时误差,簇Gi的误差定义为

(15)

设计权值学习规则为

(16)

其中γ1,γ2分别为两类传播信号参与调整神经网络的权重。

4 数值仿真实验

根据3.2节所述,系统参数设置为:传感器S数目k=15,簇G的数目r=3,提取规则Г为能源矩阵的行向量求和提取,γ1=0.8, γ2=0.2,α=1, β=1,由神经网络初始化随机选择。仿真得到的簇G1的能耗特性、隐含层神经元权值特性如图2～4所示。

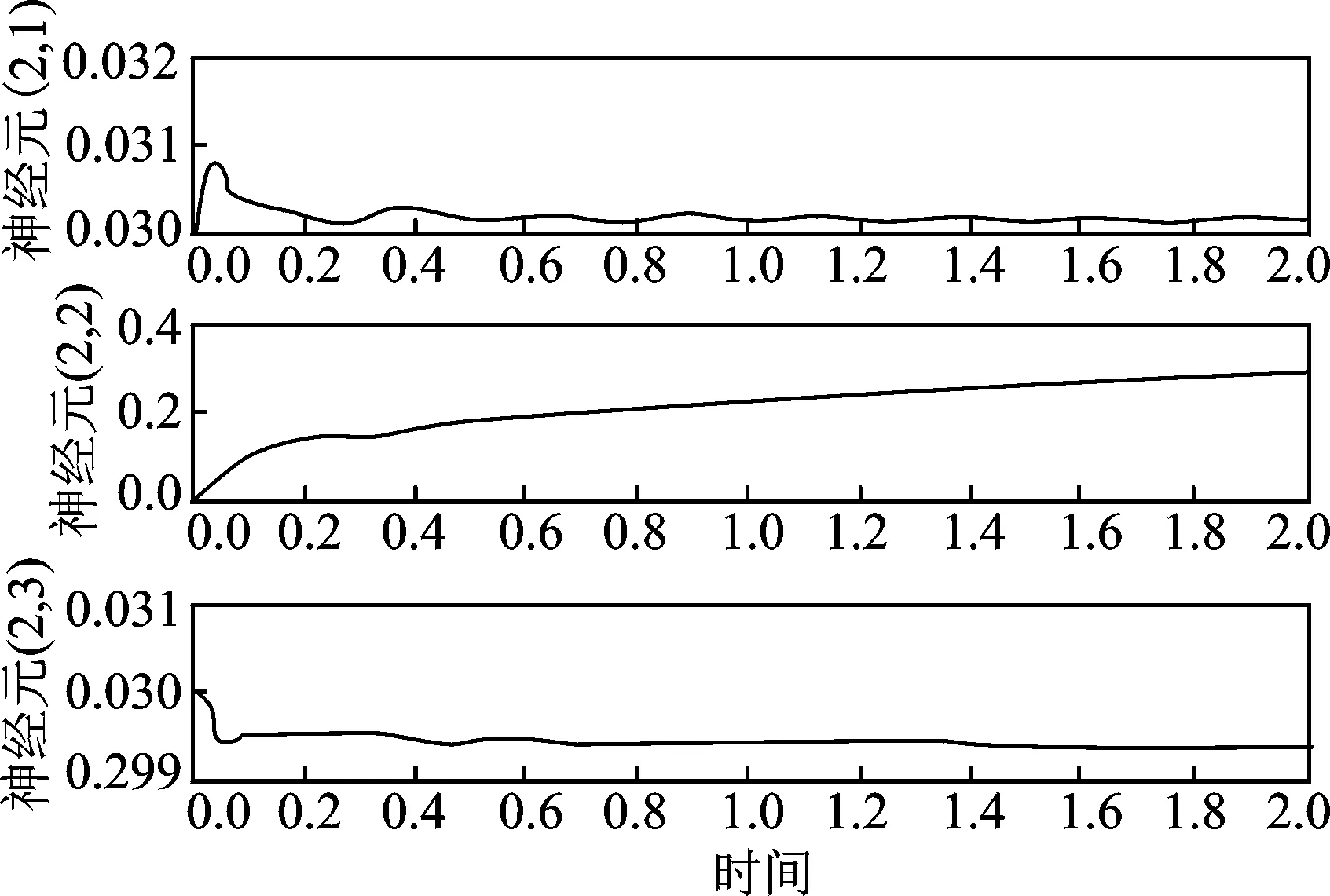
Fig.3 Part of network weight convergence

图2能耗曲线中,采用基本的全网络处理方法，在数据捕获以及发送的前期,系统并没有大量耗能,然而一旦进入发送处理环节,系统能耗便会增加,但是整体能耗趋势下滑迅速;从图3可以看到,随机给定网络的初始权值,经过系统的自适应学习收敛到最佳的常值网络，系统的自适应能力较强。WSN自适应方法随着权值学习的稳定而能耗逐步减小。需要注意的是,对于中型以上的网络体系,图3中采用自适应的策略能够从网络底层便开始处理数据,虽然计算能耗多一些,但是对于下一阶段的数据处理是必要的。全网络的误差收敛迅速，甚至在第25步时，新生成的神经网络中neurons=25,MSE=0.850 551，Goal=0.001,这也符合图4中的能耗变化特征曲线。

5 结束语

本文提出了无线传感器网络的系统化建模分析方法，为无线传感器网络的应用提供了一个模型化的计算模式。由于孤立的或者局部的能源函数分析和输出准确性分析也被考虑在内,所以在不同的应用背景下，通过参数调节或者更新系统控制矩阵便可以得到较强适应力的全局调度系统。实际上，通过配置节点的拓扑组成完成全局优化是动态过程，本文给出的算例也表明了该建模方法的有效性及动态自适应能力。下一步的工作将集中解决以下问题。首先，需要更加系统的模型包含输入矩阵,如何加入系统调节矩阵来完善系统的自动化和智能化；其次，对于一个监测区域内的源节点，怎样完成多类数据的采集以及分发处理，同时需要考虑一旦系统故障如何快速响应(如实时环境下某些监测项突变对系统的危害，需要快速上报敏感数据项等)。大规模并行计算算法可以更好地减少冗余，但是带来了网络成本上升以及网络时延，这些需要综合考虑。

[1] Zhang X.Adaptive control and reconfiguration of mobile wireless sensor networks for dynamic multi-target tracking[J].IEEE Transactions on Automatic Control,2011,56(10):2429-2444.

[2] Szczodrak M,Gnawali O,Carloni L P. Dynamic reconfiguration of wireless sensor networks to support heterogeneous applications[C]∥2013 IEEE International Conference on Distributed Computing in Sensor Systems (DCOSS). Cambridge:IEEE,2013: 52-61.

[3] Tahir M,Javaid N,Iqbal A. On adaptive energy-efficient transmission in WSNs[J]. International Journal of Distributed Sensor Networks,2013,1:1-10.

[4] Wu Wei,Zhong Sheng,Zhou Guopeng. A study on PID intelligent optimization based on radial basis function neural networks[C]∥2013 3rdInternational Conference on Consumer Electronics,Communications and Networks (CECNet). Xianning,Hubei:IEEE,2013: 57-60.

[5] Pantazis N A,Vergados D D. A survey on power control issues in wireless sensor networks [J]. Communications Surveys & Tutorials,IEEE,2007,9(4): 86-107.

[6] 张德干,戴文博,牛庆肖. 基于局域世界的WSN拓扑加权演化模型[J]. 电子学报,2012,40(5): 1000-1004.

Zhang Degan ,Dai Wenbo,Niu Qingxiao.Local-world weighted topology evolving model for wireless sensor networks[J].ACTA Electronica Sinica,2012,40(5): 1000-1004.

[7] 邹学玉,曹阳. 基于能耗预测的WSN单跳路由分簇算法术[J]. 华南理工大学学报：自然科学版,2008,36(5):13-18.

Zou Xueyu,Cao Yang. Forecasted energy dissipation-based clustering a lgorithm of single-hop routing protocol for wireless sensor networks[J].Journal of South China University of Technology:Natural Science Edition,2008,36(5):13-18.

[8] 顾云丽,徐昕,杜杰,等. 基于区域不相交的无线传感网任播路由算法[J]. 系统工程与电子技术,2013,35(10): 2086-2092.

Gu Yunli,Xu Xin,Du Jie,et al.Any cast routing algorithm based on zone-disjoint scheme of wireless sensor networks[J].Systems Engineering and Electronics,2013,35(10): 2086-2092.

[9] Aquino A L,Carlos M， S,et al. Data stream based algorithms for wireless sensor networks applications[C]∥21st International Conference on Advanced Networking and Applications.Ontario:IEEE,2007:869-876.

[10]Landau I D,Lozano R,M′saad M. Adaptive control [M]. Berlin: Springer,1998,15-22.

[11]王聪,陈填锐,刘腾飞. 确定学习与基于数据的建模及控制[J]. 自动化学报,2009,6: 693-706.

Wang Cong,Chen Tianrui,Liu Tengfei. Deterministic learning and data-based modeling and control[J]. ACTA Electronica Sinica,2009,6: 693-706.

[12]王建平,陈改霞,孔德川,等.一种基于学习自动机的WSN区域覆盖算法[J]. 数据采集与处理,2014,29(6):1016-1022.

Wang Jianping,Chen Gaixia,Kong Dechuan,et al. Learning automata-based area coverage algorithm for wireles sensor networks[J].Journal of Data Acquisition and Processing, 2014,29(6):1016-1022.

[13]张玲华,姚绍芹,解伟超. 基于自适应粒子群优化径向基函数神经网络的语音转换[J]. 数据采集与处理,2015,30(2):336-343.

Zhang Linghua,Yao Shaoqin,Xie Weichao.Voice conversion based on adaptive particle swarm optimization radial basis function neural network[J]. Journal of Data Acquisition and Processing, 2015,30(2):336-343.

钟杰卓(1981-)，女，高级工程师，研究方向：云计算及虚拟化技术，分布式计算和大数据挖掘，E-mail:zjiezhuo@126.com。

杜文才(1953-)，通讯作者，男，博士，教授，博士生导师，研究方向：信息与通信工程和物联网等，E-mail:Wucai@hainnu.edu.cn。

吴慰(1989-)，男，硕士研究生，研究方向：数据与知识工程、人工智能和控制理论与控制工程等，E-mail:Wuweiisle@163.com。

Adaptive Systemic Modeling for Wireless Sensor Networks

Zhong Jiezhuo, Du Wencai, Wu Wei

(College of Information Science and Technology, Hainan University， Haikou, 570228, China)

Global energy consumption in wireless sensor networks restricts the application of the entire networks, including the impact of limited energy capacity of a single node to the system fundamentally. This paper presents a systemic modeling approach for wireless sensor network based on radial basis function neural networks and status-sphere expression. In consideration about the topology and hierarchical structure of WSN, it introduces real-time adjusting of radial basis function neural networks, and establishes matrix model for systematic energy consumption adaptively. Results prove that this model performs effective global optimization by adjusting parameters according to real application circumstances.

wireless sensor networks; radial basis function neural networks; control theory; dynamic optimization

国家自然科学基金(61162010)资助项目；海南大学教育教学研究课题(Hdjy1325)资助项目；海南大学青年基金课题(Qnjj1186)资助项目；海南省研究生创新科研课题(Hys2014-18)资助项目；海南省自然科学基金(614232)资助项目；海南省产学研一体化专项基金项目(CXY20140002)资助项目。

2015-05-21；

2015-10-12

TP391

A