二面角的双基地散射特性分析*

胡 程 敖东阳 曾 涛 刘飞峰

(1.北京理工大学嵌入式实时信息处理技术北京市重点实验室，北京，100081;2.北京理工大学信息与电子学院雷达技术研究所，北京，100081)



二面角的双基地散射特性分析*

胡 程1，2敖东阳1，2曾 涛1，2刘飞峰1，2

(1.北京理工大学嵌入式实时信息处理技术北京市重点实验室，北京，100081;2.北京理工大学信息与电子学院雷达技术研究所，北京，100081)

二面角效应是高分辨率 SAR 图像非常重要的特征，其主要是建筑物的墙面和地面及其他人造物体形成的二面角造成的强反射。为了减小二面角的雷达散射截面积(Radar cross section,RCS)，常用的技术是改变二面角的几何结构。双基地雷达是一种几何配置灵活的雷达，具有一定的反隐身能力。本文主要利用几何光学分析了不同张角二面角的散射特性及其SAR图像表现形式。针对二面角的多次散射问题，计算了散射次数和最终出射角度的通项公式，并给出了双基地条件下二面角RCS的定量计算公式。仿真结果表明，不同张角的二面角RCS和双基地雷达的几何结构密切相关，在特定的双基地雷达几何配置下，二面角在双基地SAR图像中表现为角点处的强点。

二面角；双基地雷达；散射特性；SAR图像

引 言

随着合成孔径雷达(Synthetic aperture radar，SAR)成像技术的高速发展，现今已经有多种体制的SAR传感器，包括单基地SAR和双/多基地SAR。它们都广泛地应用在遥感探测及相关军事应用中，其中双基地雷达是新体制雷达中的一个研究热点。双基地SAR是一种收发分置的雷达系统，具有系统结构灵活、成本低等特点[1]。20世纪70年代末，美国率先开展了双基地SAR系统的研究工作，进行了一些理论研究和一系列机载和星载双基地SAR实验[2]，然而由于技术问题和缺乏有效的成像算法，限制了20世纪90年代后期的双基地SAR研究。进入21世纪以来，随着机载和星载SAR技术的不断进步，全球范围内掀起了双基地SAR的研究热潮。近10年以来，德国、英国陆续开展了一系列机载、星载和星地等几何配置下的双基地SAR实验，得到了非常好的实验结果[3,4]。在国内，北京理工大学[5]、中国科学院电子学研究所[6]等单位也陆续开展了双基地SAR实验和成像算法、干涉处理等方面的研究工作。与此同时，在实验的推动下，双基地SAR成像算法的研究工作也逐渐深入并且不断完善[7-9]。通过引入双基地角度这一维度，可以实现对目标区域进行双基地多波段、双基地多极化等多维度的观测，进一步挖掘目标在双基地多维度观测下的散射机理，为目标几何结构的解译、目标分类与识别提供新的技术途径与方法。

探测隐身目标是双基地雷达的一个重要优势[10]。一些目标在单基地条件下具有很小的雷达散射截面积(Radar cross section，RCS)，但是在双基地条件下情况就不一样。隐身技术主要从两方面进行研究：一是改变目标的材料特性，如使用吸波材料等；二是改变目标的几何结构，采用非常规的形状改造目标的外形。一般情况下，为了使目标的RCS更小，两种方法都会采用。当前隐身目标的几何结构都是非传统结构，如变形的二面角，经常出现在隐身舰船及飞机等目标中。这些隐身目标的出现对雷达探测的能力提出了严峻的挑战。双基地雷达具备灵活的结构，可以探测到不规则目标。因此研究目标的双基地散射特性，对于研究反隐身雷达具有重要的参考价值。二面角是一种典型的结构，其在大角度范围内拥有很大的RCS，是目标RCS的主要贡献部分。在隐身目标中，要尽可能地避免二面角结构。在城市遥感中，由建筑物的墙面和地面形成的二面角造成的强反射是SAR图像的一个重要特征[11,12]。当前的城市遥感特征的研究都基于单基地雷达体制[13,14]，对于双基地体制已经不再适用，因此，二面角结构在双基地图像中的特性需要新的理解。部分研究结果都表明双基地雷达和单基地雷达的成像能力相似[15]，但是目标的单双基地散射特性不尽相同。文献[16]提到，即使双基地角变化非常小，目标的散射特性也可以发生非常明显的变化，这种现象会对SAR目标分类带来好处。因此，研究典型目标的双基地图像的特性非常有必要，特别是不同张角的二面角的散射特性。圆迹SAR是一种非常好的雷达观测体制。与常规直线轨迹SAR 模式不同，圆迹SAR以雷达随平台作 360°圆周运动、波束始终指向同一场景区域为主要数据获取几何[17]。这种观测几何下，圆迹 SAR 通过对观测场景的 360°全方位观测，具有更好的观测能力，在目标识别方面具有重要的潜力。

本文首先利用几何光学的理论分析了不同张角的二面角在单基地和双基地情况下的主瓣方向性，同时分析了不同体制的雷达成像聚焦的位置、图像表现形式等。其次，给出了双基地二面角散射公式，描述了二面角反射的长度、张角、双基地接收机发射机位置与RCS的关系。最后，利用电磁仿真方法中的全波方法仿真了单双基地圆迹体制下的二面角回波数据，同时分析了成像结果与多次散射对成像的影响。

1 不同张角的二面角

二面角是雷达探测中经常出现的目标。众所周知，在假设场景为单次散射的情况下，单基地和双基地雷达并无差别。但是在多次散射之后，双基地雷达则显示了其特有的特性。其中，最为常见的多次散射是二面角。两块平行放置的平板相当于0°的二面角，这是一种临界状态。再次回归到二面角的散射特性。按照角度的分类，可以将二面角分为锐角、钝角和直角等几类，下面按这个分类进行讨论。

1.1 直角二面角

图1 直角二面角的几何光路图Fig．1 Beam path diagram of the rectangular dihedral corner

直角二面角广泛出现在城区建筑中，如竖直的墙面和地面会构成直角二面角结构，还有树立在地面的物体也会形成直角二面角结构。因此，直角二面角结构是最常见的目标结构。单基地雷达对直角二面角具有很强的响应，这是由于单基地雷达的发射机和接收机处在同一位置,能接收到最强的回波信号[18]。为了分析SAR成像中二面角的工作机制，首先利用几何光学的方法分析其传播光路图。直角二面角的几何光路图如图1所示。

(1)

对于2点,有

(2)

除去1点和2点两个散射体的位置所产生的距离，还有在空间中传播的距离，定义为

(3)

因此，对于单基地雷达而言，从发射回波到接收回波产生的相位差为

(4)

1.2 钝角二面角

在隐身技术中，通过改变几何结构来减小目标的RCS是一种常见的手段。在单基地雷达中，直角二面角具有很大的RCS，这不利于目标的隐身。因此，很多隐身目标都采用非直角的二面角结构。钝角二面角的雷达波反射路径如图2所示。

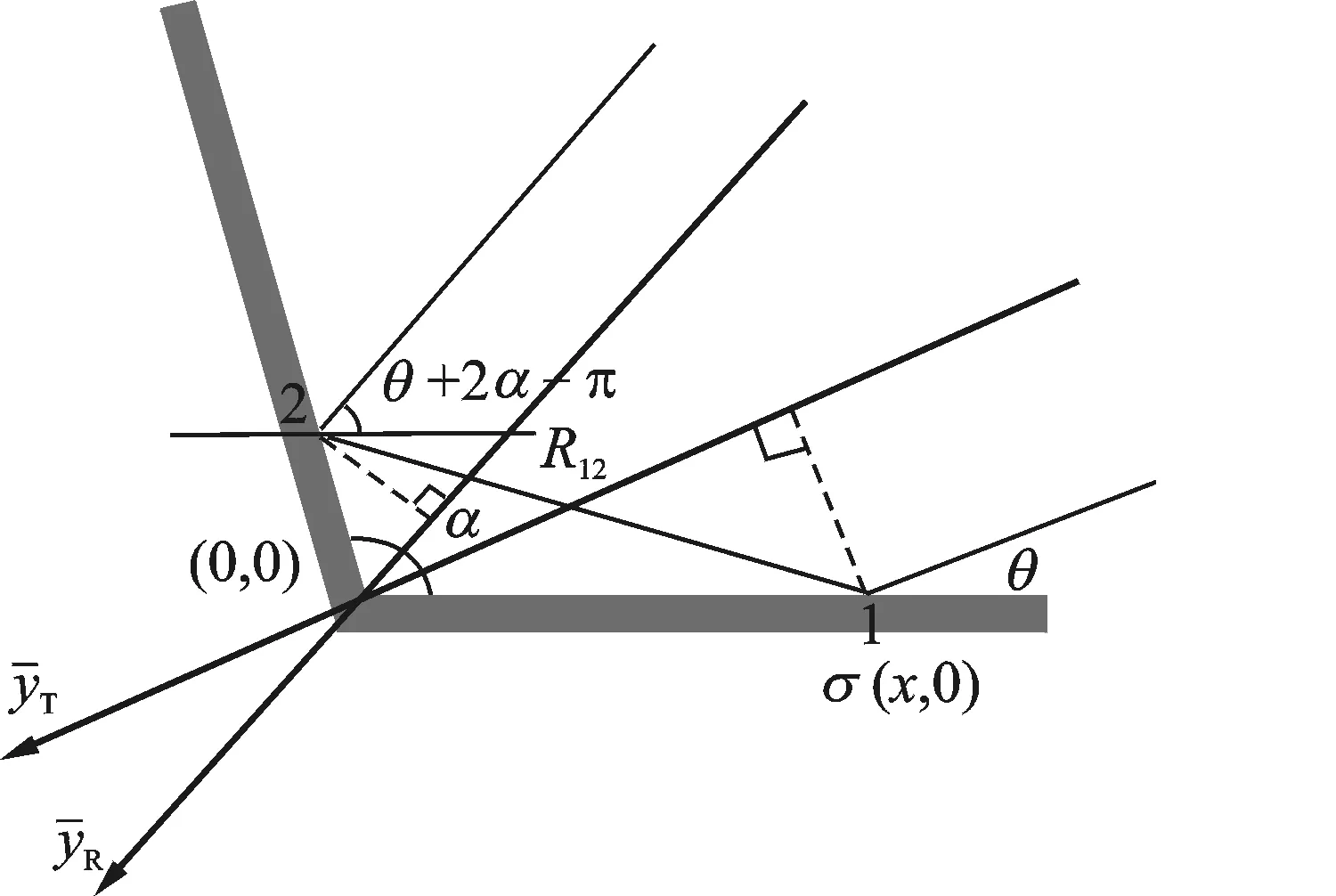
图2 双基地探测钝角二面角分析 Fig．2 Analysis of the obtuse dihedral corner in bistatic observation

由于单基地雷达无法接收到经过二次散射的波束，考虑采用双基地这一收发分置的雷达系统来探测钝角二面角。假设二面角的张角为α，基于镜面散射原理，如果入射波角度为θ，那么雷达波的主要能量将以θ+2α-π的角度反射出去。因此，如果以双基地角为2α-π的雷达去探测二面角结构，就能获得很强的目标RCS。下面将分析钝角二面角在SAR图像中的表现。同直角二面角一样，首先分析波束传播过程。

(5)

打到1之后，会产生较强的反射波，打到2处，2点在接收机坐标系下的坐标为

(6)

其中，y为2点到原点的距离，由正弦定理可得

(7)

化简式(6)，得到

(8)

反射波传播的过程增加了波程R12，根据正弦定理，R12为

(9)

这样，回波的相位为

(10)

和直角二面角一样，钝角二面角在特定双基地体制下的SAR图像中表现为二面角的顶点。改变二面角的张角是减小RCS的一种重要手段。

1.3 锐角二面角

锐角二面角一般不太常见，大部分文献考虑的都是锐角的尖端几何绕射[20,21]，对于角型结构的内部分析较少。直角和钝角二面角最多只能发生二次散射，而锐角二面角会存在多次散射的情况。按照散射次数分析其多次散射的情况。

1.3.1 二次散射

对于二次散射，锐角和其他两种二面角并无太大区别，如果也用π-2α的双基地角观测，也能获得和钝角和锐角一样的效果。锐角二面角的反射路径如图3所示。

图3 锐角二面角的2次散射Fig．3 Double-bounce scattering of the acute dihedral corner

图4 锐角二面角的3次散射Fig．4 Three-bounce scattering of the acute dihedral corner

1.3.2 多次散射

4次散射的条件为3α+θ<π，以此类推，可以得到多次散射发生的规律，如表1所示。

表1 多次散射满足的条件和出射角度

在直角和钝角的讨论中，得到如下结论：直角和钝角二面角在特定的双基地角观测情况下，在SAR图像中的表现形式等效为二面角顶点处的强点。原因是经过二次散射后的波程和二面角顶点处的波程一致。如图5所示，可以画出等效直线传播的锐角二面角的多次散射传播路径图。由几何关系可知，AB=CD，又可证明ΔOAD≌ΔOED，那么就有OA=OE。负的波程为OB+OE，正的波程为CD=OA+OB=OE+OB，那么总的波程可以等效为到原点的波程。因此可以断定锐角二面角在特定的双基地角下的SAR成像形式也是一个点。

图5 锐角二面角的多次散射等效波束传播Fig．5 Equivalent beam path in multiple-bounce case of the acute dihedral corner

2 二面角RCS计算

目前已经有相关文献[22]讨论过改变二面角张角减小RCS的问题，但是双基地结构下的二面角散射公式还没有文献发表。本文将考虑双基地条件下的二面角RCS计算公式。为了简化问题，不考虑电磁波的边缘衍射。二面角是由两块平板组成的结构。因此，首先要分析的是平板的双基地RCS公式。平板的几何结构如图6所示。

图6 平面的双基地散射图Fig．6 Bistatic scattering of a flat surface

(11)

2.1 二面角理论分析

一个二面角的RCS由4部分构成：Sa,Sb是两个平面贡献的，Sab,Sba则是二次弹跳散射贡献的。因此，二面角的RCS可以写成

(12)

对于入射角-β<φ<β，可以直接利用计算单次散射贡献的RCS

(13)

(14)

对于两个平面的二次弹跳散射，实际有效的二面角长度(面积)会发生变化，一个平面的二次散射并不会完全照射到另一个面上。这种情况相对复杂，可以从图7中分析得到等效平面长度。

图7 二面角等效平面计算 Fig．7 Calculation of dihedral corner equivalent flat surface

由图7可知，等效长度的计算公式为

(15)

同理，可得另一种情况下的等效长度

(16)

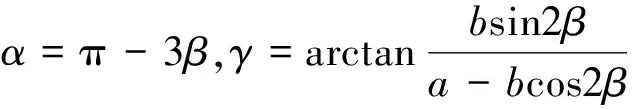
将等效的长度代入式(11)，即可计算出二次散射的值

(17)

同理，可以得到另一个二面角的值

(18)

最终，可以将双基地照射下的二面角RCS公式化简成以下形式

(19)

式中Rm,Pm和Qm等参数如表2所示。其中2β为二面角的张角，φ为入射角，θ为接收角。至此得到了双基地观测下二面角的RCS散射公式。

表2 式(19)参数列表

2.2 二面角RCS公式验证

为了验证公式的正确性，利用式(19)进行仿真，并检验其是否符合第二部分的结论，最后验证是否和全波电磁仿真的结果一致。首先，对于直角二面角，利用单基地雷达探测，可以预测其在0°～90°之间会有较强的RCS。RCS公式计算结果如图8所示。

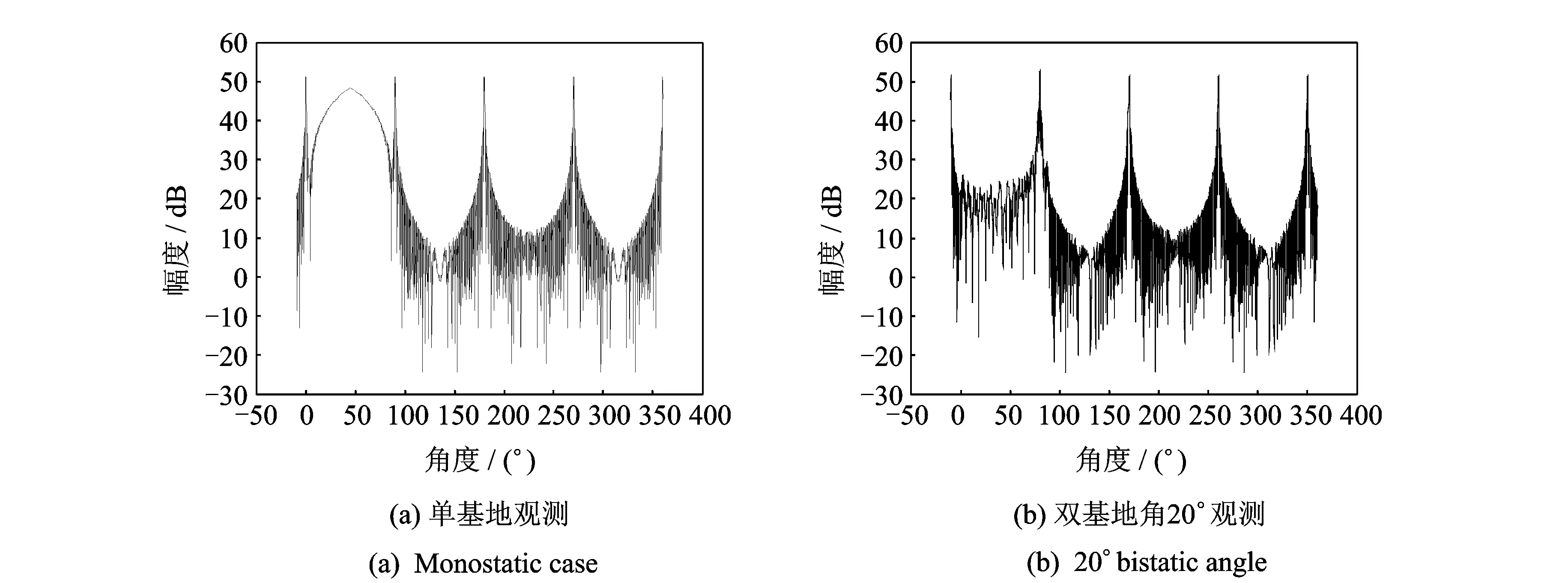
图8 直角二面角RCSFig．8 RCS of the 90° dihedral corner

从图8中，可以得知，在0°～90°范围内，单基地雷达能获得很强的RCS，相反，双基地雷达则无法探测到。其中的尖峰位置是由平板的镜面散射所致，只在某些特定角度下出现。对于120°张角的二面角，分别使用单基地雷达，双基地角为60°和20°的双基地雷达进行RCS分析。其结果如图9所示。从图9可知，只有在特定的双基地角观测下，才能够在一定范围内观测到很强的RCS，并且双基地角符合第二部分的理论分析。

图9 120°二面角RCSFig．9 RCS of the 120° dihedral corner

由于多次散射的分析较为复杂，式(19)不再适用，同时多次散射之后会存在衰减。因此分析最多考虑到二次散射。式(19)只是一个近似公式。至此，完成了各种形态的二面角在不同雷达体制下的RCS计算。

3 二面角的SAR图像仿真

本节分析直角二面角、钝角二面角及其他形状二面角的SAR成像结果，并对比单双基地条件下的SAR图像的异同。回波数据通过矩量法仿真得到。矩量法是一种全波分析方法，能够仿真出各种情况的散射。仿真的体制是圆迹聚束SAR，参数如表2所示。仿真场景如图10所示。接收机与发射机分置，图中标出了双基地角，中间的物体则是不同张角的二面角。

图10 仿真示意图Fig．10 Sketch map of simultions表2 仿真参数Tab.2 Simulation parameters

载频/GHz10带宽/GHz2频率步进间隔/MHz40角度方位/(°)0～359角度间隔/(°)0．1初始距离/m30000

3.1 直角二面角

仿真实验设置中间的目标是直角二面角，合成孔径范围为40°～50°。用单基地雷达去照射(图11)，从之前的波程分析可以看出，最终的结果是一个点。用20°双基地角的双基地雷达去照射(图12)，合成孔径范围和单基地雷达一致。

图11 直角二面角的单基地成像结果Fig．11 SAR image in monostatic case of the rectangular dihedral corner

对比直角二面角的单双基地雷达成像结果，单基地雷达能获得很强的目标响应，而双基地雷达则不行。但是，可以使用双基地雷达来规避这种常见的二面角物体，文献[24]仿真分析表明，双基地雷达可以探测到隐藏在树林里的军事目标。由于树林中的树和地面能构成很多的直角二面角结构，车辆等目标很容易隐藏其中，而双基地则可以避免自然目标形成的直角二面角，从而能够探测到处于隐藏状态的车辆目标。

3.2 钝角二面角

设置中间的目标物体为钝角二面角，分别用单基地、不同双基地角的雷达对其进行成像，验证之前获得的结论。首先是单基地雷达的仿真情况(图13)。由以前的分析可知，单基地雷达无法获得很强的目标RCS。

再使用20°双基地角进行仿真，结果如图14所示。从图14可以看出，在不合适的双基地角下，也很难观测到类似的强点目标。当使用60°双基地角观测是，所得的结果如图15所示。可以看出，当选用合适的双基地角时，钝角二面角才会表现出很强的RCS。对于钝角二面角，只有很少一部分雷达体制能够观测到此类二面角散射体。因此，改变二面角张角是一种非常有效的隐身技术。

图12 直角二面角的20°双基地角成像结果Fig．12 Bistatic SAR image in 20° of the rectangular dihedral corner

图13 钝角二面角的单基地成像结果Fig．13 SAR image in monostatic case of the obtuse dihedral corner

图14 钝角二面角的20°双基地单基地成像结果Fig．14 Bistatic SAR image in 20°bistatic angle of the obtuse dihedral corner

图15 钝角二面角的60°双基地单基地成像结果Fig．15 Bistatic SAR image in 60°bistatic angle of the obtuse dihedral corner

3.3 锐角二面角

由于锐角二面角存在多次散射，同时多次散射存在衰减，一般只考虑2次散射，3次及以上的散射都不考虑。因此，对于锐角二面角，能探测到强点的双基地角公式和钝角二面角一致。例如，对于80°角的锐角二面角，就可以用π-2α=20°的双基地角去观测。同样地，使用单基地和双基地分别对其进行成像。单基地的成像结果如图16所示。对锐角二面角用20°双基地角成像，结果如图17所示。

图16 锐角二面角的单基地成像结果Fig．16 SAR image in monostatic case of the acute dihedral corner

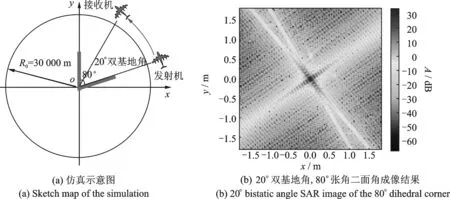
图17 锐角二面角的20°双基地成像结果Fig．17 Bistatic SAR image in 20°bistatic angle of the acute dihedral corner

本节中，对于不同张角的二面角进行了SAR成像仿真，验证了二面角这一基本结构在SAR图像中的表现形式，同时也展示了双基地雷达探测二面角的能力。灵活的几何配置是双基地雷达的一个重要优点。在目标探测中，双基地雷达对二面角这一几何结构具有很强的探测能力。在SAR图像分析中，双基地图像中的强点则蕴含着更丰富的信息，包括角点的位置、二面角的张角等。

4 结 论

本文分析了二面角这一基本几何结构在不同双基地角下的雷达散射特性，利用几何光学的方法定性地给出了二面角的散射机理，并且给出了部分形态二面角的RCS定量计算公式，比较了不同双基地角下的二面角的SAR图像特征。二面角效应广泛地存在雷达观测场景中，尤其是建筑物墙体和人造目标。改变二面角的张角是一种非常有效的隐身手段，它改变了雷达波镜面散射产生回波的方向，使单基地雷达丧失探测这类结构的能力。双基地雷达由于其灵活的几何配置，可以接受到二面角反射的主要能量，从而具备反隐身的能力。本文首先基于几何光学的镜面散射原理，分析了二面角中雷达波束的传播路径，给出了散射次数和最终出射角度的通项公式。其次，基于等效平面的思想，定量地给出了不同张角二面角的双基地RCS计算公式，并结合几何分析验证了公式的正确性。最后，利用矩量法仿真了不同二面角的RCS，并对其进行了SAR成像。在特定的雷达几何配置下，二面角的图像可以表现为角点处的强点，这些特定的角度和几何光学得出的角度一致。通过对二面角的双基地散射特性进行分析，给出了二面角这一特定结构的RCS和对应的方法，从理论上论证了双基地雷达的反隐身性能，对于扩展双基地雷达的应用具有一定的意义。同时，对于SAR成像来说，二面角的图像表现也能很直观地从文中得出结论。由于本文只考虑了二面角结结构，还是有一定的局限性。接下来的工作是分析其他典型结构的双基地散射特性，充分利用双基地雷达灵活的几何结构，从而更好地探测和识别目标。

[1] Zeng T, Ao D, Hu C, et al. Multiangle BSAR imaging based on BeiDou-2 navigation satellite system: Experiments and preliminary results[J]. Geoscience and Remote Sensing, IEEE Transactions on, 2015, 53(10): 5760-5773.

[2] Martinsek D, Goldstein R. Bistatic radar experiment[C]//EUSAR'98- European Conference on Synthetic Aperture Radar. Friedrichshafen, Germany:[s.n.], 1998: 31-34.

[3] Sanz-Marcos J, Lopez-Dekker P, Mallorqui J J, et al. SABRINA: A SAR bistatic receiver for interferometric applications[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(2): 307-311.

[4] Ender J H G. Signal theoretical aspects of bistatic SAR[C]//International Geoscience and Remote Sensing Symposium.Toulouse, France: IEEE, 2003, 3: 1438-1441.

[5] Zeng T, Wang R, Li F, et al. A modified nonlinear chirp scaling algorithm for spaceborne/stationary bistatic SAR based on series reversion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 3108-3118.

[6] Qiu X, Hu D, Ding C. An improved NLCS algorithm with capability analysis for one-stationary BiSAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(10): 3179-3186.

[7] 郭宝锋, 尚朝轩, 高梅国, 等. 机动目标双基地 ISAR 越距离单元徙动校正算法[J]. 数据采集与处理, 2014, 29(4): 562-569.

Guo Baofeng, Shang Chaoxuan, Gao Meiguo, et al.Correction algorithm of migration through resolution cells in bistatic ISAR of maneuvering target[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 562-569.

[8] 何友, 张财生. 无源双基地雷达广义相参检测性能分析[J]. 数据采集与处理, 2014, 29(4): 486-495.

He You, Zhang Caisheng. Generalized coherent detection performance analysis for passive bistatic radar[J]. Journal of Data Acquisition and Processing, 2014, 29(4): 486-495.

[9] 徐旭宇,牛朝阳,李小波,等.空间色噪声环境下双基地MIMO雷达多目标角度估计和互耦自校正[J].数据采集与处理,2014,29(5):735-742.

Xu Xuyu, Niu Chaoyang, Li Xiaobo, et al. Multi target angle estimation and mutual coupling self calibration of bistatic MIMO radar in spatial colored noise[J]. Journal of Data Acquisition and Processing,2014,29(5):735-742.

[10]Jackson J A. Analytic physical optics solution for bistatic, 3D scattering from a dihedral corner reflector[J]. Antennas and Propagation, IEEE Transactions on, 2012, 60(3): 1486-1495.

[11]Brunner D, Bruzzone L, Ferro A, et al. Analysis of the double bounce scattering mechanism of buildings in VHR SAR data[C]//Proc SPIE Conf Image Signal Process, Remote Sens XIV.Cardiff, UK: SPIE, 2008: 15-18.

[12]Yongmei J, Diannong L. A physics-based UWB FOPEN SAR man-made target detector[C]//Signal Processing Proceedings, ICSP′98, 1998 Fourth International Conference on. Beijing: IEEE, 1998: 1465-1468.

[13]范菊红, 王月清. 二面角反射器的 RCS 特性分析[J]. 舰船电子工程, 2006 (2): 148-150.

Fan Juhong, Wang Yueqing. Analysis of RCS characteristic of dihedral corner reflectors[J]. Ship Electronic Engineering,2006 (2): 148-150.

[14]杨志国, 王亮, 黄晓涛, 等. UWB SAR 目标检测中的二面角模型改进[J]. 现代雷达, 2007, 29(11): 64-67.

Yang Zhiguo, Wang Liang, Huang Xiaotao, et al. Improvement of dihedral angle model in UWB SAR target detection[J]. Modern Radar, 2007, 29(11): 64-67.

[15]Burkholder R J, Gupta I J, Johnson J T. Comparison of monostatic and bistatic radar images[J]. Antennas and Propagation Magazine, IEEE, 2003, 45(3): 41-50.

[16]曾涛. 双基地合成孔径雷达发展现状与趋势分析[J]. 雷达学报, 2013, 2(4): 329-341.

Zeng Tao.Bistatic SAR: State of the art and development trend[J]. Journal of Radars, 2013, 2(4):329-341.

[17]洪文. 圆迹 SAR 成像技术研究进展[J]. 雷达学报, 2012, 1(2):124-135.

Hong Wen. Progress in circular SAR imaging technique[J]. Journal of Radars, 2012, 1(2): 124-135.

[18]Ertin E, Austin C D, Sharma S, et al. GOTCHA experience report: Three-dimensional SAR imaging with complete circular apertures[C]//Defense and Security Symposium, International Society for Optics and Photonics. Bellingham: SPIE,2007: 656802-656802-12.

[19]Zeng Tao, Ao Dongyang,Hu Cheng, et al. Comparison between monostatic and bistatic SAR image based on spatial spectrum analysis[C]//IET International Radar Conference 2015. Xi′an: IET, 2015: 1-6.

[20]Rigling B D, Moses R L. GTD-based scattering models for bistatic SAR[C]//Defense and Security， International Society for Optics and Photonics. Bellingham: SPIE, 2004: 208-219.

[21]Griesser T, Balanis C A. Dihedral corner reflector backscatter using higher order reflections and diffractions[J]. Antennas and Propagation, IEEE Transactions on, 1987, 35(11): 1235-1247.

[22]Knott E. RCS reduction of dihedral corners[J]. Antennas and Propagation, IEEE Transactions on, 1977, 25(3): 406-409.

[23]Gordon W B. Far-field approximations to the Kirchoff-helmholtz representations of scattered fields[J]. Antennas and Propagation, IEEE Transactions on, 1975, 23(4): 590-592.

[24]Ulander L M H, Martin T. Bistatic ultra-wideband SAR for imaging of ground targets under foliage[C]//Radar Conference, 2005 IEEE International.Virginia: IEEE, 2005: 419-423.

胡程(1981-)，男，博士，博士生导师，研究员，研究方向:新体制成像雷达、雷达信号处理，E-mail：cchchb@163.com。

敖东阳(1991-)，男，博士研究生，研究方向:双基地雷达信号处理，雷达图像处理与解译,E-mail：aodongyang@qq.com。

曾涛(1971-)，男，博士，博士生导师，研究员，研究方向：雷达系统、雷达信号处理和新体制雷达，E-mail：zengtao@bit.edu.cn。

Bistatic Scattering Characteristic Analysis of Dihedral Corner Reflector

Hu Cheng1，2， Ao Dongyang1，2, Zeng Tao1，2, Liu Feifeng1，2

(1.Beijing Key Laboratory of Embedded Real-Time Information Processing Technology,Beijing Institute of Technology, Beijing, 100081, China; 2.Radar Research Lab,Beijing Institute of Technology，Beijing, 100081, China)

Dihedral corner effect is an important characteristic of SAR images, especially for the strong scatters generated by buildings and other human-made objects. Changing the opening angle of the dihedrals is a popular method to reduce radar cross section(RCS). Bistatic radar, which has flexible geometric configuration, is a good way to detect stealth targets. This paper analyzes the bistatic scattering characteristic of different dihedral corner reflectors using geometrical optics methods. As for the multiple scattering effect in the dihedral corners, the general term formula is given to describe the multiple scattering times and echo angles. Besides, the RCS calculation formula of dihedral corner is extended to bistatic condition. Both theory and simulation results show that bistatic radar has the ability to detect changed dihedral corners and its bistatic SAR image formation is a strong point at the corner point under a certain bistatic angle.

dihedral corner reflector; bistatic radar; scattering characteristic; SAR image

国家自然科学基金(61120106004,61225005，61427802,61471038)资助项目；长江学者奖励计划(T2012122)资助项目；科技北京百名领军人才培养工程(YETP1168)和"111"引智工程(B14010)资助项目。

2016-05-27；

2016-07-05

TN95

A