从广义采样、小波到压缩感知*
2016-12-23宋耀良
宋耀良 穆 童
(南京理工大学电子工程与光电技术学院,南京,210094)
从广义采样、小波到压缩感知*
宋耀良 穆 童
(南京理工大学电子工程与光电技术学院,南京,210094)
采样是对模拟信号进行数字化处理的关键环节。近年来,信号带宽及信息传输速率的快速增长致使采用传统采样机理的信号处理方法面临巨大挑战,小波变换与压缩感知等新型信号处理技术应运而生。在这种情况下,有必要从理论上重新审视经典的Shannon-Nyquist采样定理,研究具有普适性的信号表达与采样重构理论。本文从信号空间投影与函数表达的角度分析了信号表达的本质,介绍了Shannon传统采样与重构理论,以及由Papoulis提出的经Unser等所推广的广义采样与重构理论。从数学上重点探讨了小波变换(Wavelet transform)和压缩感知(Compressed sensing,CS)等现代信号处理及变换方法与广义采样的一致性。同时,通过线性调频(Linear frequency modulation, LFM)信号的实例仿真,说明采样与重构的关系以及在各个方法之间的异同性。
香农采样定理;插值;广义采样;小波变换;压缩感知
引 言
1928年Nyquist H在文献[1]中首次给出了采样定理,1949年Shannon C E在文献[2]中正式给出其证明。定理描述为:对于能量有限的带限信号,要想无失真地恢复,要求采样频率大于信号带宽的两倍。此后,很多文献将传统的采样定理称作Shannon-Nyquist采样定理,以下简称Shannon采样定理。在Shannon采样定理中,当采样频率低于Nyquist采样率或原信号非带限时会造成频谱混叠。由于现实中不存在理想带限(时域无限)信号,因此需要采用低通滤波器对输入信号进行滤波操作,同时在重构信号时滤除频谱的周期延拓分量。从时域上看,重构所用的插值内核Sinc函数衰减非常缓慢[3],计算效率很低,实时性差,不适于工程实现。因此,人们开始寻求更加有效的插值函数。20世纪90年代,Unser M等将B样条函数引入信号处理领域[4-6],探讨其作为插值内核的良好重构特性,为发展新的采样重构理论提供了思路。另一方面,Shannon采样所基于的理论基础Fourier变换实质上是将信号展开成三角函数的线性组合[7],无法在时域和频域同时获得良好的局部特性。同时,对非平稳信号而言,其时域各种时间统计量及频谱结构都会随着时间变化而失去统计意义[8]。因此,为了适应需要处理各种复杂形式信号的情形,小波分析应运而生。1981年Morlet给出了小波分析的概念,1987年Meyer和Mallat研究了多分辨率分析[9],使其之前构造正交小波的方法得以统一。1992年,Walter G基于小波多分辨再生核Hlibert空间建立了小波采样定理[10]。上述两种方法本质上研究的都是信号在不同基底下的表达问题,如何将这一类方法统一起来成为一个完整的理论体系,逐渐成为人们所关心的问题。1977年,Papoulis A在其文章中开始引入广义采样理论[11],对Shannon采样定理进行推广,探讨符合Nyquist采样率的条件下,基于线性时不变系统的带限信号的采样与重构问题。1998年,Unser M和Zerubia J在Papoulis A理论的基础上,将信号空间拓展到非带限情况,使信号的精确表达重构转向空间投影与信号在其子空间或投影空间的逼近[12-13]。
但是,这些推广仍然局限在对信号本身的表达与近似,并没有考虑信号中信息的表达问题,也就是信号如何向信息空间投影的问题。随着信息技术的发展,人们处理的信号具有更高的带宽,传统的采样方法使硬件的信号处理性能面临巨大的挑战;同时,人们常常需要压缩信号以减小信息传输与存储成本,使采集到的信息大部分被抛弃,从而造成资源浪费。因此,研究新的采样理论已成为必然趋势。2004年,Donoho与Candes等首次提出压缩感知理论[14-17],使采样速率完全由信号中包含的信息所决定,而不再受限于信号的带宽,打破了传统Shannon采样的局限性,在信号处理领域开辟了全新的研究方向。近年来,许多文献对采样理论在不同时期的发展做了详细的综述[18-21],从中可以看出信号采集与信号变换之间的关系。本文在分析信号处理所面临的诸多挑战与人们日益增长的各种需求的基础上,研究了传统Shannon采样定理存在的不足,说明了探索一般性的信号表达与采样理论的必要性。从信号空间投影与函数表达的角度分析了信号采样与重构的本质,在分析Shannon理想采样与重构理论、Papoulis的广义采样理论和Unser等人推广的广义采样与重构理论的基础上,从数学上探讨小波变换和压缩感知等现代信号处理和变换方法与广义采样理论的一致性。同时,以线性调频(Linear frequency modulation, LFM)信号为例,说明采样与重构的关系以及在各个方法之间的异同性。

图1 Shannon-Nyquist采样过程Fig.1 Block diagram of Shannon-Nyquist sampling process
1 Shannon-Nyquist采样与重构
传统的Shannon采样是一种针对带限信号的等距理想采样,其处理过程如图1所示。输入的连续信号x(t)经过前置滤波器变为带限信号,以Nyquist采样率进行采样获得离散信号

(1)
为了便于前置滤波器的实现,降低带外无用信号频谱重叠的影响,实际上信号的采样频率往往要比Nyquist采样率高。信号重构可通过理想低通滤波器来实现,在时域等同于采用无限长的非因果冲激响应即Sinc函数插值重构得到

(2)
物理上重构的实现只能通过非理想的低通滤波或时域上现在与过去时刻的采样值通过内插来实现,但无论是非理想的低通滤波或有限长度的插值均会产生重构误差[22]。下面以线性调频信号为例,通过仿真说明采样与重构的关系。假设原始信号的脉宽为1 ms,带宽为30 kHz(后文的仿真参数设置与此相同)。采样频率取70 kHz,具体仿真结果见图2。

图2 基于Shannon采样定理的LFM信号仿真结果Fig.2 Simulation results of LFM signal based on Shannon′s sampling theorem
可以看出,当采样频率为70 kHz时基本上能够无失真地恢复原始信号,有重构误差是因为在Matlab中Sinc函数取值必须进行截断,对应频谱是非理想低通滤波器,从而造成误差。由图2(b)上图可知,重构误差随采样频率的增大而减小,当采样频率低于Nyquist采样率(60 kHz)时,重构误差将迅速上升。图2(b)下图则表示重构误差随Sinc函数加窗截断后长度的增加而减小,当点数取无限长时理论误差为零。因此,Shannon采样的重构精度同时受采样频率与插值内核的长度影响,而工程实现上不可能采用过高的采样频率与过长的插值长度,这正是Shannon采样局限性的体现。
2 广义采样与插值
由式(2)可以发现,{sinc(t-n),n∈Z}是一个线性无关且相互正交的函数族。为了理解正交性,可以从空间中函数投影的角度来考虑。设f(x),g(x)为空间中的连续函数,则f(x)在g(x)上的投影可用它们的内积表示
(3)
由此定义,可得
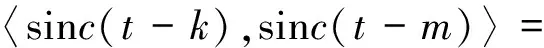
(4)
由式(4)可以看出,sinc函数在时间轴上的平移函数族构成了所有带限函数组成的函数空间的一组正交基。将上述结论推广至更为一般的情形,这里定义一个基本近似空间V,即
(5)
它表示空间V内任意的连续函数s(x)都能够表示为系数c(k)的序列。
为了使建立的模型具有实际意义,需要对其设置一些限制条件。系数序列必须平方可和;函数组{φk=φ(x-k)}k∈Z必须构成空间V(φ)的一组Riesz基[23]。Riesz基的定义为:一定存在两个正常数0≤A,B≤+∞,使得
(6)


图3 广义采样过程Fig.3 Block diagram of generalized sampling process
信号的采样及重构,实际上就是对给定的信号,通过选取合适的基,使信号在这组基下的投影具有所需要的性质,如果在某个基下不符合要求,那么就将其变换到另一个基下表示。后文所提到的短时Fourier变换、小波变换以及压缩感知中的稀疏变换,都是基于这种广义上的采样理论思想所进行的。与Shannon采样对应,这里给出广义采样的处理框架如图3所示。
将连续信号与基函数求内积、采样并经过一个数字校正滤波器,得到其在该基底上的离散展开系数,再由广义上的重构公式即可恢复原始信号。这里讨论一个比较典型的基函数——B样条函数[24-25]。0阶B样条函数定义为
(7)
将它与自身迭代相乘,便得到k阶B样条函数
(8)
除了0阶以外,高阶的B样条函数并不是相互正交的,但其均满足Riesz基限制条件,同时具有紧支撑以及良好的逼近特性,在投影重构中优于无紧支性且衰减缓慢的sinc函数[26-27],且其实现成本较低,更具有工程应用价值。基于3阶B样条函数对LFM信号投影与重构的仿真见图4。

图4 3阶B样条函数对LFM信号投影重构结果Fig.4 Projection and reconstruction results of LFM signal using three order B-spline function
由图4(a)可以看出,3阶B样条时域衰减很快,避免了sinc函数截断带来的重构误差,同时可以非常准确地重构出原始LFM信号。经计算得到重构误差为1.26×10-14,这是由于前置滤波器与重构滤波器的冲激响应是相互正交的,仿真从频域上实现,对应频谱乘积为1,因此理论误差为零,产生的误差是由Matlab计算精度有限导致。
3 采样与小波变换
Fourier变换在研究时域信号的局部特性及处理非平稳信号上性能并不理想。1946年,Gabor给出短时Fourier变换,利用窗函数限制计算范围,使其简单局部化。然而,由于窗函数在变换过程中始终保持不变,因此较好的局部特性只能在时域或频域内获得,而不能同时获得[28]。
希望找到这样一种基函数,能够满足以下特性:(1)任何复杂的信号都可通过该基函数的尺度与位置变化所产生的基底进行表达;(2)信号在该基底下的展开系数能够反映其时域局部特性;(3)该基函数针对非平稳信号拥有较强的匹配特性。
1909年,Haar首次发现了这样的基函数,即著名的Haar小波[29]

(9)
函数ψ(t)∈L2(R)称为基本小波,如果它符合该“允许”条件
(10)

(11)
将a,b进行变量替换,令a=2-j,b=2-jk,便可得到离散小波变换[8]
(12)
式中:ψj,k(t)=2j/2ψ(2jt-k)。
数学上已经证明:{ψj,k(t)=2j/2ψ(2jt-k)|j,k∈Z}构成了L2(R)的一组规范正交基,任意能量有限的信号f(t)∈L2(R)可以在该组基下表示为
(13)

图5 Haar小波对LFM信号分解与重构结果Fig.5 Decomposition and reconstruction results of LFM signal using Haar wavelet
其中离散展开系数cj,k=〈f(t),ψj,k(t)〉,也即式(12)所表示的离散小波变换。
小波在时域上紧支,同时也正负交替振荡,对信号进行小波分析可以在信号的时域及频域同时获得良好的局部特性,可以用来处理非平稳信号,并且能在多尺度下由粗到细地分析信号,聚焦到信号的任何细节[8,30]。基于Haar小波对LFM信号分解重构的仿真如图5所示。由此可以看出,小波分解能够同时获取LFM信号的低频信息与高频信息。低频信息反映了原始LFM信号的平均趋势,而高频信息则反映了其波动趋势,即随着频率的增加波动越来越剧烈,这也与客观事实相符。相对于Fourier变换只能分析信号的频域特性,利用小波变换可以在不同尺度上研究并处理信号。例如当信号混入噪声时,对其小波分解后得到的高频信息做适当处理便可达到去噪的效果[31]。与B样条重构一样,小波重构的误差同样来源于Matlab计算误差,其为3.78×10-15。
4 采样与压缩感知
以Shannon采样定理为指导的采样方法没有突破Nyquist采样率的限制,这对信号尤其是宽带信号的处理能力及硬件设备的性能造成了极大的挑战,寻求一种新的数据处理方法已成为必然。2004年Donoho,Candes等首先给出压缩感知理论,该理论表明:若信号投影到某个域内具备稀疏性或可压缩性,那么采用较少的信号测量值就能以高概率恢复原始信号[14-15]。
考虑长度为N的信号x,若其在基底Ψ上K-稀疏,则可表示为x=Ψα,利用测量矩阵Φ得到x的测量值y=Φx=ΦΨα。记Θ=ΦΨ,当Θ满足受限等距特性(RIP)准则时[32],就可通过求解y=Θα的逆问题得到α,再代入式x=Ψα即可将原始信号x从测量投影值y中正确地恢复[33]。压缩感知适用的基本前提有两个,分别是信号的稀疏性,以及测量矩阵与稀疏基的非相关性[34]。
CS理论的信号重构问题等价于稀疏约束下的欠定方程求解
(14)
由于对上式的求解是个NP-hard问题[35],因此将‖α‖l0松弛为‖α||l1,转化为l1最小范数下的最优化问题
(15)
基于该思想的重构算法主要包括内点法与梯度投影法[36],随后又有人提出新的贪婪算法,大大提高了计算速度,且易于实现,如匹配追踪(Matching pursuit, MP)法[37],正交匹配追踪(Orthogonal matching pursuit, OMP)法[38]以及分段OMP法[39],等。
压缩感知能够以低速率同时对信号进行采样和压缩,大大减小了传感器的计算压力与数据的传送、储存成本。经过10年多的发展,压缩感知理论在诸多工程技术领域已有广泛的应用,例如超宽带信号处理[40-42]、高分辨雷达成像[43-45]、模式识别[46-48]以及医疗成像[49-51]等。与此同时,压缩感知目前也存在一些问题和瓶颈,主要集中在数学理论上,例如测量矩阵与稀疏基的非相关性难以保证,迭代算法过程不可控,重构算法复杂度高、运算速度慢等[52]。应用压缩感知理论对LFM信号进行测量并用OMP算法进行重构的仿真如图6所示。

图6 基于压缩感知的LFM信号仿真结果Fig.6 Simulation results of LFM signal based on compressed sensing
仿真中,对原始信号进行快速傅里叶变换可以得到其在频域的稀疏度K,若信号长度为N,则由关系式M≥K×log(N/K)可以得到测量次数M。测量向量由高斯分布随机矩阵与LFM信号时域相乘得到,见图6(a)上图。由图6(a)下图可以看出,仿真利用较少的测量值完成了对LFM信号较为准确的重构。在满足M≥K×log(N/K)的条件下,重构误差随测量次数的增大而减小。同时,重构误差对测量次数的变化并不敏感,且始终保持在小于1的范围内。因此,压缩感知相对于传统Shannon采样具有更加高效、低成本的特性,在处理带宽更大、稀疏度更高的信号时,其优越性将更加明显。
5 结束语
Shannon采样定理作为通信与信号处理领域的一个重要基本结论,为信号的数字化处理奠定了基础。而随着信息技术的发展,传统采样方法所存在的问题正在逐步显现出来,使其已无法满足当下各种信息获取需求。本文针对Shannon采样从时域插值重构、时频特性分析,以及应对宽带信号处理能力等方面理论分析了其存在的缺陷,并通过仿真验证,从而分别引出广义采样、小波变换,以及压缩感知理论,介绍了其发展历程与基本原理,从数学角度探讨了它们所基于的共同思想,并通过仿真说明其基本实现方法以及相对于传统方法所具有的优越性。文中所述的这些方法和理论,不论是对Shannon采样定理的发展、扩充还是突破,其本质都是将信号变换到新的基底或者域内表达,使其表现出所需要的某种特性,再通过构造函数或算法将信号无失真或近似地恢复,从而实现滤波、去噪和压缩等功能。从香农采样到广义采样、小波变换再到压缩感知,新的信号处理方法在不断地发展并完善,以适应更加丰富多变的信息环境,而广义采样作为一种普适性的信号表达与采样理论,既是对现有的信号处理方法规律的总结,也为开拓新的理论提供了思路。因此深入理解并研究广义采样对信号处理技术的发展与创新具有广阔而深远的意义。
[1] Nyquist H. Certain topics in telegraph transmission theory[J]. Transactions of the American Institute of Electrical Engineers, 1928, 47(2): 617-644.
[2] Shannon C E. Communication in the presence of noise[J]. Proceedings of the IRE, 1949, 37(1): 10-21.
[3] Parker J A, Kenyon R V, Troxel D E. Comparison of interpolating methods for image resampling[J]. Medical Imaging, IEEE Transactions on, 1983, 2(1): 31-39.
[4] Unser M, Aldroubi A, Eden M. B-spline signal processing. I. Theory[J]. Signal Processing, IEEE Transactions on, 1993, 41(2): 821-833.
[5] Unser M, Aldroubi A, Eden M. B-spline signal processing II. Efficiency design and applications[J]. IEEE Transactions on Signal Processing, 1993, 41(2): 834-848.
[6] Unser M. Splines: A perfect fit for signal and image processing[J]. Signal Processing Magazine, IEEE, 1999, 16(6): 22-38.
[7] Welch P D. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms[J]. IEEE Transactions on Audio and Electroacoustics, 1967, 15(2): 70-73.
[8] Merry R J E, Steinbuch M. Wavelet theory and applications[R]. Literature Study, Eindhoven University of Technology, Department of Mechanical Engineering, Control Systems Technology Group, 2005:3-13.
[9] Mallat S G. A theory for multiresolution signal decomposition: The wavelet representation[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1989, 11(7): 674-693.
[10]Walter G G. A sampling theorem for wavelet subspaces[J]. IEEE Transactions on Information Theory, 1992, 38(2): 881-884.
[11]Papoulis A. Generalized sampling expansion[J]. IEEE Transactions on Circuits and Systems, 1977, 24(11): 652-654.
[12]Unser M, Aldroubi A. A general sampling theory for nonideal acquisition devices[J]. Signal Processing, IEEE Transactions on, 1994, 42(11): 2915-2925.
[13]Unser M, Zerubia J. A generalized sampling theory without band-limiting constraints[J]. Circuits and Systems II: Analog and Digital Signal Processing, IEEE Transactions on, 1998, 45(8): 959-969.
[14]Donoho D L. Compressed sensing[J]. Information Theory, IEEE Transactions on, 2006, 52(4): 1289-1306.
[15]Candès E J. Compressive sampling[C]//Proceedings of the International Congress of Mathematicians. Madrid: European Mathematical Society, 2006, 3: 1433-1452.
[16]Candè E J, Wakin M B. An introduction to compressive sampling[J]. Signal Processing Magazine, IEEE, 2008, 25(2): 21-30.
[17]Tsaig Y, Donoho D L. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3): 549-571.
[18]Jerri A J. The Shannon sampling theorem—Its various extensions and applications: A tutorial review[J]. Proceedings of the IEEE, 1977, 65(11): 1565-1596.
[19]Unser M. Sampling 50 years after Shannon[J]. Proceedings of the IEEE, 2000, 88(4): 569-587.
[20]Vaidyanathan P P. Generalizations of the sampling theorem: Seven decades after Nyquist[J]. Circuits and Systems I: Fundamental Theory and Applications, IEEE Transactions on, 2001, 48(9): 1094-1109.
[21]Wu Guochang, Zhang Yadong, Yang Xiaohui. Sampling theory: From Shannon sampling theorem to compressing sampling[J]. Information Technology Journal, 2010, 9(6): 1231-1235.
[22]林茂六, 尹宝智, 刘治宇. 高速采样信号数字内插理论与正弦内插算法研究[J]. 电子学报, 2000, 28(12): 8-10.
Lin Maoliu, Yin Baozhi, Liu Zhiyu. Digital interpolation theory and sinc interpolation algorithm on high-speed sampling signals[J]. Acta Electronica Sinica, 2000, 28(12): 8-10.
[23]Daubechies I, Heil C. Ten lectures on wavelets[J]. Computers in Physics, 1992, 6(6): 697-697.
[24]Schoenberg I J. Contributions to the problem of approximation of equidistant data by analytic functions, Part B: On the problem of osculatory interpolation, a second class of analytic approximation formulae[J]. Quart Appl Math, 1946, 4(2): 112-141.
[25]Schoenberg I J. Cardinal interpolation and spline functions: II interpolation of data of power growth[J]. Journal of Approximation Theory, 1972, 6(4): 404-420.
[26]Aldroubi A, Unser M, Eden M. Cardinal spline filters: Stability and convergence to the ideal Sinc interpolator[J]. Signal Processing, 1992, 28(2): 127-138.
[27]Meijering E H W, Niessen W J, Viergever M A. The Sinc-approximating kernels of classical polynomial interpolation[C]//Image Processing, Proceedings 1999 International Conference on. [S.l.]: IEEE, 1999, 3: 652-656.
[28]Aldroubi A. Families of wavelet transforms in connection with Shannon sampling theory and the Gabor transform[J]. Wavelets: A Tutorial in Theory and Applications, 1992: 509-528.
[30]Daubechies I. The wavelet transform, time-frequency localization and signal analysis[J]. Information Theory, IEEE Transactions on, 1990, 36(5): 961-1005.
[31]Ghael S P, Sayeed A M, Baraniuk R G. Improved wavelet denoising via empirical Wiener filtering[C]//Optical Science, Engineering and Instrumentation′97. Bellingham: SPIE, 1997: 389-399.
[32]Foucart S, Lai M J. Sparsest solutions of underdetermined linear systems via lq-minimization for 0 [33]Candès E J, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. Information Theory, IEEE Transactions on, 2006, 52(2): 489-509. [34]李卓凡, 闫敬文. 压缩感知及应用[J]. 微计算机应用, 2010 (3): 12-16. Li Zhuofan, Yan Jingwen. Theory and application of compressive sensing[J]. Microcomputer Applications, 2010 (3): 12-16. [35]Hochba D S. Approximation algorithms for NP-hard problems[J]. ACM SIGACT News, 1997, 28(2): 40-52. [36]Figueiredo M A T, Nowak R D, Wright S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. Selected Topics in Signal Processing, IEEE Journal, 2007, 1(4): 586-597. [37]Neff R, Zakhor A. Very low bit-rate video coding based on matching pursuits[J]. Circuits and Systems for Video Technology, IEEE Transactions on, 1997, 7(1): 158-171. [38]Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. Information Theory, IEEE Transactions on, 2007, 53(12): 4655-4666. [39]Donoho D L, Tsaig Y, Drori I, et al. Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J]. Information Theory, IEEE Transactions on, 2012, 58(2): 1094-1121. [40]Eldar Y C. Compressed sensing of analog signals in shift-invariant spaces[J]. IEEE Transactions on Signal Processing, 2009, 57(8): 2986-2997. [41]Shi G, Lin J, Chen X, et al. UWB echo signal detection with ultra-low rate sampling based on compressed sensing[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2008, 55(4): 379-383. [42]Dai W, Milenkovic O. Weighted superimposed codes and constrained integer compressed sensing[J]. IEEE Transactions on Information Theory, 2009, 55(5): 2215-2229. [43]Herman M A, Strohmer T. High-resolution radar via compressed sensing[J]. IEEE Transactions on Signal Processing, 2009, 57(6): 2275-2284. [44]Yoon Y S, Amin M G. Compressed sensing technique for high-resolution radar imaging[C]//SPIE Defense and Security Symposium. [S.l.]: International Society for Optics and Photonics, 2008: 69681A-69681A-10. [45]黄琼, 屈乐乐, 吴秉横, 等. 压缩感知在超宽带雷达成像中的应用[J]. 电波科学学报, 2010(1): 016. Huang Qiong, Qu Lele, Wu Bingheng, et al. Compressive sensing for ultra-wideband radar imaging[J]. Chinese Journal of Radio Science, 2010(1): 16. [46]Elad M. Optimized projections for compressed sensing[J]. IEEE Transactions on Signal Processing, 2007, 55(12): 5695-5702. [47]Mairal J, Bach F, Ponce J, et al. Discriminative learned dictionaries for local image analysis[C]//IEEE Computer Vision and Pattern Recognition. New York: IEEE, 2008: 1-8. [48]Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. [49]Lustig M, Donoho D, Pauly J M. Sparse MRI: The application of compressed sensing for rapid MR imaging[J]. Magnetic Resonance in Medicine, 2007, 58(6): 1182-1195. [50]Provost J, Lesage F. The application of compressed sensing for photo-acoustic tomography[J]. IEEE Transactions on Medical Imaging, 2009, 28(4): 585-594. [51]Trzasko J, Manduca A. Highly undersampled magnetic resonance image reconstruction via homotopic-minimization[J]. IEEE Transactions on Medical imaging, 2009, 28(1): 106-121. [52]焦李成, 杨淑媛, 刘芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 39(7): 1651-1662. Jiao Licheng, Yang Shuyuan, Liu Fang, et al. Development and prospect of compressive sensing[J]. Acta Electronica Sinica, 2011, 39(7): 1651-1662. 宋耀良(1980-),男,教授,研究方向:超宽带雷达、超宽带通信和现代信号处理技术,E-mail:ylsong@mail.njust.edu.cn。 穆童(1993-),男,博士研究生,研究方向:雷达信号处理和微波成像。 From Generalized Sampling and Wavelet to Compressed Sensing Song Yaoliang, Mu Tong (School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing, 210094, China) Sampling is the key procedure for the digital processing of analog signal. In recent years, signal processing methods employing traditional sampling mechanism have faced tremendous challenges due to the rapid growth of signal bandwidth and information transmission rate, and some new signal processing technology such as the wavelet transform and the compressed sensing emerged at the right moment. On this occasion, it is necessary to reexamine the classical Shannon-Nyquist sampling theorem in theory, and study universal expression, sampling and reconstitution theory of signal. The nature of signal expression is analyzed from the point of view of signal projection and function representation. Firstly, the Shannon traditional sampling and reconstruction theory, and the generalized sampling and reconstruction theory proposed by Papoulis and extended by Unser are introduced. Then, the consistency between modern signal processing and transforming methods (wavelet transform, compressed sensing) and generalized sampling theory is investigated mathematically. Meanwhile, the chirp signal is taken as a simulation example to illustrate the relationship between signal sampling and reconstruction, as well as the similarities and differences in each method. Shannon′s sampling theorem; interpolation; generalized sampling; wavelet transform; compressed sensing 国家自然科学基金(61271331,61571229)资助项目。 2016-05-29; 2016-07-02 TN911.7 A

