互耦效应下多组相干源的波达方位估计算法*
2016-12-23季正燕陆晓飞
陈 辉 李 帅 季正燕 陆晓飞
(空军预警学院3系,武汉,430019)
互耦效应下多组相干源的波达方位估计算法*
陈 辉 李 帅 季正燕 陆晓飞
(空军预警学院3系,武汉,430019)
对于实际环境中存在的多径现象和阵元间的互耦效应,提出一种互耦效应下针对相干源的波达方向估计算法。首先,通过波达方向矩阵法利用二阶矩求出互耦效应下的广义导向矢量;然后对广义导向矢量进行子空间平滑,通过矩阵变换得到一个线性约束下的规划问题,实现相干源方位和互耦系数的级联估计。该算法只需利用二阶矩求得广义导向矢量,相比常规的四阶累积量方法,减少了计算量;本文算法在解互耦和解相干过程中都没有损失阵列孔径,极大提高了阵元利用效率。计算机仿真结果验证了该算法的有效性。
波达方向估计;互耦;解相干;广义导向矢量
引 言
空间谱估计在最近30年来得到飞速发展,广泛应用于雷达、通信、地震科学和生物科学等领域[1]。人们已经从基础理论研究转向实际情况下的具体应用,其中阵元间的互耦误差和相干信号源的情况是空间谱估计在实际应用中不可避免的,这两者都会严重影响传统空间谱估计算法的性能[2,3]。相干源的存在导致了信号子空间的秩小于信号源的个数,传统子空间类算法性能急剧恶化。针对相干信号源的问题,常见的解决方法有空间平滑、矩阵重构和Toeplitz方法等[4-6],这些方法不考虑信号源之间具体的相干情况,本质上是将信号协方差矩阵进行秩恢复;文献[7~9]提出了一类子空间平滑算法,将相干源分组,依次对每组相干源进行时域平滑,提高了阵元的利用效率,可以估计多于阵元数目的信号波达方向。阵元间的互耦效应导致阵列流型的改变,会严重影响常规DOA估计算法的性能。针对互耦效应下的空间谱估计,主要有以下几类方法:(1)通过测量、内插以及存储等方法实现互耦校正,这类算法实现代价较大而且效果不明显;(2)借助辅助信号源对误差参数进行离线估计的有源校正方法,这类算法运算量较小,但是需要已知信号源的精确方位;(3)实现对信号源方位和互耦系数联合估计的自校正方法,自校正方法可以实现在线估计,相对有源校正方法,不会由于环境变化引入新的扰动。文献[2,3,10~12]是一类互耦自抑制方法利用了均匀线阵互耦矩阵的带状Toeplitz性,截取中间阵元的接收数据(或者等效的在阵列两侧补充辅助阵元),将互耦系数剥离出阵列流形,并将其归入新构造的信号协方差矩阵。这类方法实现简单,借助内在机制“自动”消除互耦影响,但是损失了部分阵元自由度,导致可估计信源数减少。文献[13~16]则是一类秩损(RAnk-REduction, RARE)解互耦方法,这种方法利用了整个阵列的数据,基于子空间原理和互耦矩阵的结构特点,可以实现对信源方位和互耦系数的联合估计。然而之前提出的大部分自校正算法还是假设信号源独立,与实际情况相差较远。通过查阅文献,目前能够实现同时解相干和解互耦的方法相对较少。其中文献[2,3,10]提出了一类同时实现解互耦和解相干的方法,利用了互耦自抑制的原理和平滑或者矩阵重构的方法解相干,这类方法计算量相对较小,但是解互耦和解相干过程中都损失了一定的阵元自由度,可估计信号数目也因此大大减少。文献[17]基于加权空间平滑算法,构建了阵列误差条件下的代价函数,通过遗传算法进行幅相误差校正;文献[18]针对有源校正中的多径传播问题,基于最大似然准则建立了阵列误差、校正源多径传播方位和多径衰减系数的优化模型利用牛顿迭代算法实现优化。这两者对于存在阵列误差时对相干源的方位估计有一定参考意义,但是受限于高维非线性优化的大计算量。本文针对均匀线阵,建立了互耦效应下多组相干源入射的模型,通过二阶矩和波达方向(Direction of arrival, DOA)矩阵法得到每组相干源的广义导向矢量,然后利用移动通信环境中多径衰减特性,采用子空间平滑方法,同时将互耦系数从阵列流形中去耦合,实现对组内多径信号的DOA估计,而且可以精确估计出互耦系数。本文提出的方法适用于雷达阵列信号处理,解决了雷达测角中存在的多径影响及有源干扰问题,而且考虑了阵元间的互耦效应,可以实现互耦校正。
文中符号说明:[·]T表示转置,[·]*表示共轭,[·]H表示转置共轭,toeplitz(·)表示以括号中矢量作为第一行的Toeplitz矩阵,diag(·)表示由括号中的矢量构成对角阵,E[·]表示统计均值。
1 阵列模型
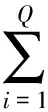
(1)
式中:a(θji)=[1,ejφ,…,ej(M-1)φ],φ=2πd/λsinθ为理想的导向矢量,d表示阵元间距;θji表示第i组信号源第j条多径的波达方位;zji为第i组信号源第j条多径的衰减系数;si(t)为第i组信号源直达径的复包络;n(t)为M×1维噪声矢量;C为互耦矩阵,有
(2)
式(1)可以写成矩阵形式

(3)
其中
(4)
(5)
(6)
(7)
(8)
互耦效应下的广义阵列流型可以写为
(9)
(10)
式中bi为互耦效应下的广义导向矢量。
2 互耦效应下相干源估计方法
文献[7~9]是一类基于四阶累积量和子空间平滑的方法,利用四阶累积量得到广义导向矢量bi,根据移动通信环境中不同路径上衰减特性,对信号源组进行子空间平滑,实现信号源的DOA估计,文献[19]通过外场实验证明了子空间平滑的有效性。四阶累积量的计算量较大,而且考虑阵元间的互耦效应时,阵列流型产生扰动,会导致原有算法失效。本文提出了互耦效应下基于二阶矩和子空间平滑的相干源估计方法。
2.1 基于二阶矩的广义导向矢量估计方法
DOA矩阵法是一种高效的波达方向估计方法,其具体阐述参见文献[20],这种方法的一个重要作用是可以得到阵列的导向矢量。DOA矩阵法的关键是对角阵φ的构造,之前文献中有利用阵列平移不变结构的和利用四阶累积量的方法。文献[21]提出了时空DOA矩阵的方法,利用阵元接收数据的互相关函数将空域观测数据变换到时空域,利用了信号时间维的信息,不再要求阵列结构具有平移不变性,而且避免了四阶累积量的大计算量。文献[22]针对盲源分离问题提出了利用二阶矩和联合对角化的方法,也是利用时域信息避免了四阶累积量的计算。除了利用阵列结构信息或者通过四阶累积量计算提取更多信息,还可以充分利用时间维上的信息,这里考虑利用两个不同时延的相关矩阵构造出对角阵φ。
假设噪声为均值为零,方差为σ2的加性高斯白噪声,各阵元间的噪声、Q组信号源相互独立,即
(11)
(12)
(13)
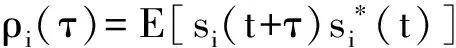
(14)
(15)
式中I为M×M维的单位矩阵。
取不同的时延0,τ≠0,根据式(14,15),得出接收数据的相关矩阵
(16)
(17)
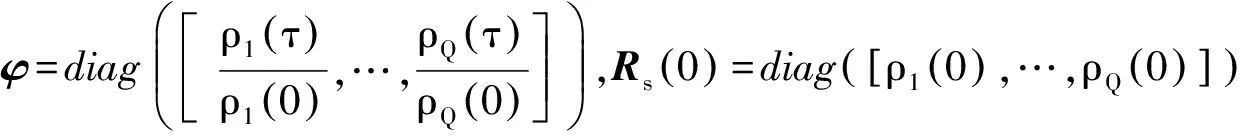
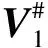
2.2 波达方向及互耦系数估计
在典型的移动通信环境中,多径衰落系数是快变化的,这是由于信号波长较短引起的,比如信号载频为1 GHz时,信号波长只有30 cm,多径变化15 cm会导致信号相位改变180°。另外,由于目标与基站之间距离较远,在较短时间内,直达径和多径的波达方向是慢变化的。所以在较短时间内,互耦矩阵和阵列流型是不变的,而多径衰落系数是随机变化的(特别是衰落系数的相位可以看作服从均匀分布)。这就是子空间平滑的原理,基于此可以在这段时间里求得互耦效应下广义导向矢量的L个估计值,即
(18)

(19)
然后取L个相关矩阵的平均,可得
(20)
由于多径衰减矢量zi是快变化的,所以第i组相干源的信号子空间,即Rzi是满秩的,从而实现了组内解相干。根据常规的MUSIC算法,将得到
(21)
其中Ui是Rbi特征分解后M-Pi个小特征值对应的特征矢量阵,据此可以得到如下优化问题,即
(22)
这是一个高维非线性优化问题,采用常规的参数搜索类算法会带来较大的计算量,而且可能出现局部收敛的情况,所以应采用将信号波达方向与互耦系数“去耦”的方式,以减少计算量。首先将Ca(θ)进行变换,其中互耦矩阵可以表示为
(23)
式中:Ei(i,j)=δ(C-ci),则
(24)
式中:T=[T1(θ),…,Tm(θ)],Ti(θ)=Eia(θ),c=[c1,c2,…,cm]T为互耦系数矢量。将式(24)代入式(22)可得
(25)

(26)

(27)
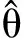
(28)
3 仿真分析
3.1 空间谱曲线
仿真采用八阵元均匀线阵,阵元间距为半波长。阵元间互耦系数为c1=1,c2=0.623 7+j0.387 5,c3=0.365 8+j0.231 6,ci=0,i>3。两组相干源由复高斯信号经过一阶AR模型滤波产生,AR模型系数分别是0.95ej1.5和0.85ej0.55,两组相干源信噪比分别为10,5dB。第1组相干源有4条多径,入射角度分别是-30°,-10°,30°和50°,第2组相干源有3条多径,入射角度分别是-50°,10°和70°。假设多径衰减系数幅度和相位分别服从(0:1)和(-π:π)的均匀分布,各多径的衰减系数相互独立。仿真中快拍数为128,时延τ=10。本文算法对两组相干源估计的空间谱如图1所示。

图1 本文算法对两组相干源估计的空间谱Fig.1 Spectrum of two groups of coherent signals by proposed method
在互耦系数已知或者不考虑互耦的情况下,本文方法最多可以估计信号源的个数为:8组×7个/组。不过存在未知互耦系数时,每组最多可以估计的信号源数为5,这是由于解互耦的过程中,互耦系数的估计也需要占用两个自由度,导致每组内可估计信源数目为5。相对文献[3]中的算法,通过利用阵列性质解互耦后,其有效阵元数目减少为4,所以其可以估计的信号源数最多为4(这是信号源互不相关的情况,当存在相干信号源时,由于还要进行平滑处理,能估计信号源数目更少)。
3.2 波达方向估计性能
通过仿真比较本文算法与文献[3]的算法在不同信噪比下的方位估计性能,其中本文算法采用8阵元均匀线阵,阵元间距为半波长,文献[3]的算法采用15阵元均匀线阵,阵元间距同样为半波长,平滑时子阵阵元数为6。两者阵列互耦系数设置、两组相干源产生同3.1节,假设两组相干源的多径数目分别为2和3,其中第1组的入射角度分别为-10°和10°,第2组的入射角度为-30°,30°和50°。仿真中,首先,固定第2组相干源信噪比为5 dB,第1组相干源信噪比从-10~25 dB,仿真比较两种算法对第1组相干源波达方向的估计性能;然后,固定第1组相干源信噪比为5 dB,第2组相干源信噪比从-10~25 dB,仿真比较两种算法对第2组相干源波达方向的估计性能。DOA估计性能与信噪比关系如图2所示。从仿真结果可以看出,在文献[3]方法使用阵元数(15)是本文算法使用阵元数(8)的近两倍时,本文算法估计的准确度和精确度明显好于文献[3]方法。
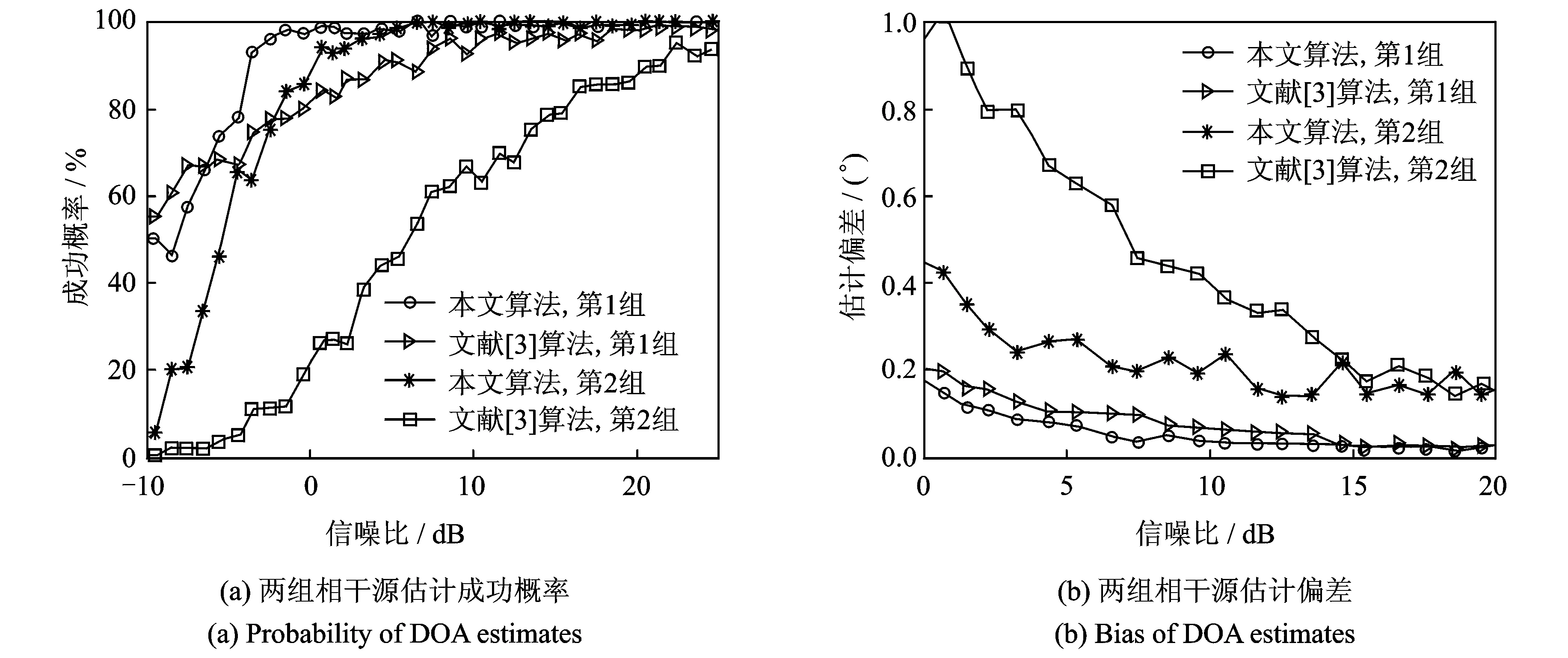
图2 DOA估计性能与信噪比的关系Fig.2 Performance of DOA estimation versus SNR
3.3 互耦系数估计性能
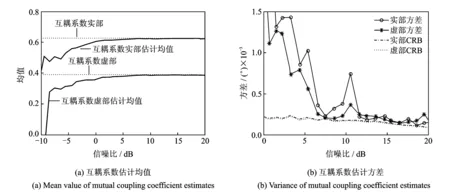
图3 互耦系数估计性能与信噪比关系Fig.3 Performance of mutual coupling coefficient estimation versus SNR
仿真条件同3.2节,固定第2组相干源信噪比为5 dB,第1组相干源信噪比从-10~25 dB,利用本文算法估计得到互耦系数c2的性能结果如图3所示。从图3中可以看出, 本文算法对互耦系数具有较高的估计精度,随着信噪比增加,估计均值逐渐逼近实际值,当信噪比大于12 dB时,估计方差接近克劳美罗界(CRB),说明了本文算法可以实现互耦校正。
3.4 时延对算法性能影响
利用两个相关矩阵求得互耦效应下的广义导向矢量bi是本文算法的关键步骤,bi的估计精度直接决定了后续子空间平滑和互耦校正的效果,所以仿真不同时延下信号方位和互耦系数的估计性能。实验中两组信号源信噪比分别为10,5 dB,快拍数为128,时延分别取从0~100,其他条件同3.2节,仿真结果来自500次蒙特卡洛实验。波达方向、互耦系数估计性能与时延关系如图4所示。从图4中可以看出,时延大于0快拍小于20个快拍时,随着时延增加,方位估计成功概率逐渐下降、互耦系数估计均值与实际值偏差逐渐增大、波达方位和互耦系数估计方差逐渐增大,而当时延大于20个快拍时,各项指标基本保持平稳。可以得出,当时延为2~5时本文算法性能最好。时延的增加会导致计算相干矩阵时的数据量(快拍数-时延数)减少,从而导致性能下降。
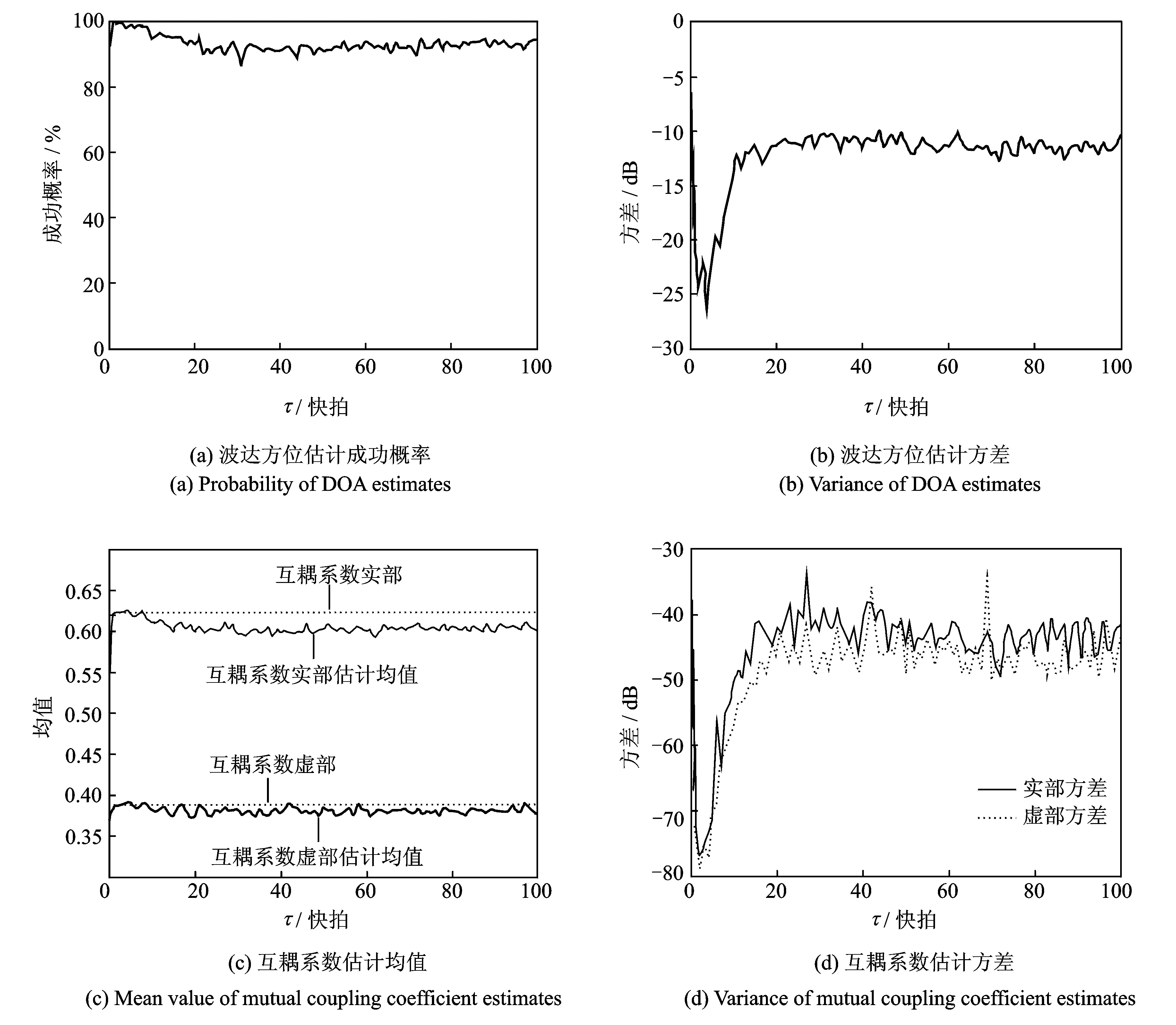
图4 波达方位、互耦系数估计性能与时延关系Fig.4 Performance of DOA and mutual coupling coefficients estimation versus time delay
4 结束语
相干源的存在导致了信号协方差矩阵的秩小于信号数目,互耦效应导致阵列流形的扰动,这两者都严重影响了常规空间谱估计算法的估计性能。针对这一问题,本文通过子空间平滑实现了相干源分组及解相干,借助时延不同的相关矩阵得到广义导向矢量,计算量小于常规的四阶累积量方法;利用矩阵变换实现了波达方位和互耦系数的级联估计,不需要损失阵元自由度,避免了互耦自抑制类算法需要阵元数较多的问题。计算机仿真结果表明,本文算法可估计信号源数较多,估计精度较高而且可以实现互耦校正。
[1] Gu Jianfeng, Zhu Weiping, Swamy M. Joint 2-D DOA estimation via sparse L-shaped array[J]. IEEE Transactions on Signal Processing, 2015,63(5):1171-1182.
[2] Wang Yuexian, Trinkle M, Brian W. DOA estimation under unknown mutual coupling and multipath with improved effective array aperture[J]. Sensors, 2015,15:30856-30869.
[3] Dai J, Ye Z. Spatial smoothing for direction of arrival estimation of coherent signals in the presence of unknown mutual coupling[J]. IET Signal Processing, 2011,5(4):418-425.
[4] 吴向东,马仑,梁中华.一种改进的加权空间平滑算法[J].数据采集与处理,2015,30(4):824-829.
Wu Xiangdong, Ma Lun, Liang Zhonghua. Improved weighted spatial smoothing algorithm[J]. Journal of Data Acquisition and Prcoessing, 2015,30(4):824-829.
[5] 梁浩,李小波,王磊.采用单次快拍数据实现信源DOA估计[J].数据采集与处理,2013,28(1):58-63.
Liang Hao, Li Xiaobo, Wang Lei. DOA estimation of signals using one snapshot[J]. Journal of Data Acquisition and Prcoessing, 2013,28(1):58-63.
[6] 韩勇,乔晓林,金铭,等.基于Toeplitz矩阵的酉变换波达角估计算法[J].数据采集与处理,2011,26(1):52-56.
Han Yong, Qiao Xiaolin, Jin Ming, et al. Unitary transformation DOA algorithm based on Toeplitz matrix[J]. Journal of Data Acquisition and Prcoessing, 2011,26(1):52-56.
[7] Yuen N, Friedlander B. DOA estimation in multipath: An approach using fourth-order cumulants[J]. IEEE Transactions on Signal Processing, 1997,45(5):1253-1263.
[8] Gonen E, Dogan M C, Mendel J M. Applications of cumulants to array processing: Direction finding in coherent environment[C]∥28th Asilomar Conference on Signal, system and Computer. Pacific Grove, CA, USA: IEEE, 1995,1:633-637.
[9] 景小荣,隋伟伟,周围.基于四阶累积量和时间平滑的相干信号DOA估计[J].系统工程与电子技术,2012,4(34):789-794.
Jing Xiaorong, Sui Weiwei, Zhou Wei. DOA estimation of coherent signals based on fourth-order cumulant and temporal smoothing[J]. Systems Engineering and Electronic, 2012,4(34):789-794.
[10]Mao Weiping, Li Guolin, Xie Xin, et al. DOA estimation of coherent signals based on direct data domain under unknown mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2014,13:1325-1328
[11]徐旭宇,牛朝阳,李小波,等.空间色噪声环境下双基地MIMO雷达多目标角度估计和互耦自校正[J].数据采集与处理,2014,29(5):735-742.
Xu Xuyu, Niu Chaoyang, Li Xiaobo, et al. Multi-target angle estimation and mutual coupling self-calibration of bistatic MIMO radar in spatial colored noise[J]. Journal of Data Acquisition and Prcoessing, 2014,29(5):735-742.
[12]Ye Zhongfu, Dai Jisheng, Xu Xu, et al. DOA estimation for uniform linear array with mutual coupling[J]. IEEE Transactions on Aerospace and Electronic Systems, 2009,45(1):280-288.
[13]Dai Jisheng, Bao Xu, Hu Nan, et al. A recursive RARE algorithm for DOA estimation with unknown mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2014,13:1593-1596.
[14]司伟建,吴迪,陈涛,等.一种阵列互耦矩阵与波达方向的级联估计方法[J]. 电子与信息学报, 2014,36(7):1599-1604.
Si Weijian, Wu Di, Chen Tao, et al. Cascade estimation method of mutual coupling matrix and direction of arrival[J]. Journal of Electronics and Information Technology, 2014,36(7):1599-1604.
[15]Liao Bin, Zhang Zhiguo, Chan Shingchow. DOA estimation and tracking of ULAs with mutual coupling[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012,48(1):891-905.
[16]Lin M, Yang L. Blind calibration and DOA estimation with uniform circular arrays in the presence of mutual coupling[J]. IEEE Antennas and Wireless Propagation Letters, 2006,5:315-316.
[17]王布宏,王永良,陈辉.多径条件下基于加权空间平滑的阵元幅相误差校正[J].通信学报,2004,25(5):166-174.
Wang Buhong, Wang Yongliang, Chen Hui. Array gain and phase calibration in the presence of multipath based on weighted spatial smoothing[J]. Journal of China Institute of Communications, 2004,25(5):166-174.
[18]王鼎,吴瑛.多径条件下的乘性阵列误差有源校正算法[J].中国科学:信息科学,2015,45:270-288.
Wang Ding, Wu Ying. The multiplicative array errors calibration algorithms in the presence of multipath[J]. Science in China Series E: Information Sciences, 2015,45:270-288.
[19]Jeng Shiann-Shiun, Lin Hsin-Piao, Okamoto G, et al. Multipath direction finding with subspace smoothing[C]∥1997 IEEE International Conference on Acoustics, Speech, and Signal Processing. Munich, Germany: IEEE, 1997,5:3485-3488.
[20]殷勤业,邹理和,Robert W.一种高分辨率二维信号参量估计方法——波达方向矩阵法[J].通信学报,1991,12(4):1-7.
Yin Qinye, Zhou Lihe, Robert W. A high resolution approach to 2-D signal parameter estimation——DOA matrix method[J]. Journal of China Institute of Communications, 1991,12(4):1-7.
[21]金梁,殷勤业.时空DOA矩阵方法[J].电子学报,2000,28(6):8-12.
Jin Liang, Yin Qinye. Space-time DOA matrix method[J]. Acta Electronica Sinica, 2000,28(6):8-12.
[22]Belouchrani A, Abed-Meraim K, Jean-Francois C, et al. A blind source separation technique using second-order statistics[J]. IEEE Transactions on Signal Processing, 1997,45(2):434-444.

陈辉(1974-),男,教授,博士生导师,研究方向:空间谱估计、阵列信号处理等, E-mail:chhglr@sina.com。

李帅(1991-),男,通信作者,硕士研究生,研究方向:空间谱估计,E-mail:lishuaiwuhan@sina.com。

季正燕(1992-),男,硕士研究生,研究方向:空间谱估计、压缩感知等。

陆晓飞(1992-),男,硕士研究生,研究方向:天基雷达的信号处理技术。
DOA Estimation Method of Coherent Signals in Presence of Mutual Coupling
Chen Hui, Li Shuai, Ji Zhengyan, Lu Xiaofei
(Third Department, Air Force Early Warning Academy, Wuhan, 430019, China)
A method dealing with direction of arrival(DOA) of coherent signals in the presence of mutual coupling is proposed. Firstly, the generalized steering vector is obtained through DOA matrix method based on the second-order statistics. Secondly, subspace smoothing is applied to generalized steering vector and a linear constrained programming problem is obtained by matrix transform. So DOA and coefficients of mutual coupling can be estimated sequentially. Compared with the fourth-order cumulant method, the computation load is reduced with the second-order statistics. And there is no loss of array elements, which means less array elements are needed in this method. Computer simulations prove the effectivity of the proposed method.
direction of arrival(DOA) estimation; mutual coupling; decorrelation; generalized steering vector
国家自然科学基金(61072132)资助项目;信息综合控制国家重点实验室资助项目。
2016-06-05;
2016-07-01
TN957
A
