彩色图像矩不变量理论研究进展

刘 恋，郭立强

(1.淮阴师范学院物理与电子电气工程学院，江苏淮安 223300；



彩色图像矩不变量理论研究进展

刘 恋1，郭立强2

(1.淮阴师范学院物理与电子电气工程学院，江苏淮安 223300；

2.淮阴师范学院计算机科学与技术学院，江苏淮安 223300)

图像的矩不变量理论是模式识别领域的研究热点之一。有关图像的矩不变量理论多是针对灰度图像，针对彩色图像的相关研究是一个值得关注的方向。为了得到更多模式识别领域的研究科研人员对彩色图像矩不变量理论进行探索和讨论，本文对彩色图像矩不变量理论的最新进展进行综述，讨论该理论需要解决的主要问题以及对未来工作的一些展望，以期对从事图像矩不变量理论及其应用研究的科研人员有所帮助。

彩色图像；矩；矩不变量

图像矩函数的定义及其不变性是图像处理、计算机视觉与模式识别领域的研究热点之一.矩不变量集合与其它特征描述不同，它能够描述图像的全局特征，并将某一幅图像与其它图像的不同之处以其特有的几何信息表达出来.以仿生学视角来看，图像的矩不变量表征了在某些变换下人类视觉信息具有不变性，即不同模式之间具有本质差别.从数学理论来讲，矩不变量的实质是一类代数不变量.目前，越来越多的科研人员将目光聚焦于图像矩不变量的这种特征描述能力，并将其广泛地应用在目标匹配和模式识别中.

1962年，Hu首次提出了有关矩不变量的概念[1]，并开创性地推进了相关工作的开展，他以代数不变量为理论基础推导出7个相似矩不变量并将其应用于目标识别中.近几年，在国内外权威期刊发表的有关矩不变量理论的研究文章达百余篇之多，对相关文章进行简要梳理，无外乎进行如下两方面的研究：一方面是矩函数的定义，也就是选取或者构造合适的核函数来定义图像的矩函数；另一方面是矩不变量的构造，如相似不变量、仿射不变量或者其它变换下的不变量，如弹性变换.尽管越来越多的科研人员致力于矩不变量理论的研究，并发表了大量相关论文，但多数都是以灰度图像为研究对象而非彩色图像.究其原因在于矢量信号处理理论尚有待健全，目前处理彩色图像的算法都是采用分通道的形式来处理颜色信息，其缺点在于割裂了图像颜色信息的完整性，导致了各颜色通道间相关信息的丢失.

本文旨在向读者介绍彩色图像矩不变量理论的基本原理及其发展动态，希望引起更多科研人员的关注并进行讨论，为相关理论在计算机视觉与模式识别领域的应用研究提供一个新的方法.首先，我们对矩不变量理论的基本原理进行阐述；其次，对国内外有关彩色图像矩不变量理论的研究进展以及相应的成果进行介绍；最后，提出该理论需要解决的主要问题以及对未来工作的一些展望.

1 矩不变量理论

1.1 矩函数的基本定义

前面我们提及矩不变量理论主要是围绕图像矩函数的定义和矩不变量的构造来进行研究的.首先介绍图像矩函数的定义.在数学理论上，矩函数实质上是一个积分变换(严格意义上讲是泛函)，将图像f(x,y)映射到核函数φmn上，对积分结果进行适当的变换来构造相应变换下的不变量.

假设m，n为非负整数，m+n称为矩的阶数，图像f(x,y)的m+n阶矩定义如下：

M[f(x,y)](m,n)=∬R2φmn(x,y)f(x,y)dxdy.

(1)

在公式(1)中，选择不同的核函数，就会得到不同矩函数的定义.例如，当φmn=xmyn时，我们便得到几何矩[1]的定义；当φmn=(x-iy)m(x-iy)n时，我们便得到复数矩[2]的定义.无论是几何矩还是复数矩的各阶核函数都不是正交的.众所周知，在线性代数中，线性空间的正交基与其它基底相比有很好的数值性质，如去除了数据冗余性.如果公式(1)中的各阶核函数具有正交性，我们会得到正交矩的概念.例如，当φmn为勒让得多项式时，公式(1)为勒让得矩[3]；当φmn为切比雪夫多项式时，公式(1)为切比雪夫矩[4].

公式(1)是在直角坐标系中定义的，我们也可以得到极坐标系下矩的定义：

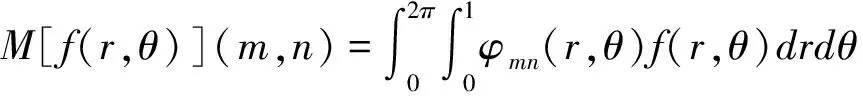
(2)

在公式(2)中，当φmn=rm-1e-inθ时，我们便得到傅里叶-梅林矩[5]的定义；当φmn为泽尼克(正交)多项式时，我们便得到了泽尼克矩[3].在使用极坐标下矩函数时，首先要把图像从直角坐标变换到极坐标，这会带来一些插值误差.但其优点是很明显的，如在极坐标下，图像的旋转可以转换为平移运算，这一点有利于不变量的构造.

1.2 矩不变量的构造方法

通过矩函数我们把图像在不同的核函数上进行投影，从不同的角度对图像进行表达.矩函数是一个积分运算，进一步讲是内积积分.不同阶数的矩是图像与相应核函数的相似程度的一个度量.从目标表达的角度来讲，还需要对这个度量值进一步处理，也就是构造相应变换下的矩不变量.接下来看一下不变量的定义.

设f(X)是定义在集合A，取值于集合B的图像，G是作用在A上的变换群.∀g∈G，∃泛函I，使得如下等式成立：

I[f(g·X)]=Δ(g)I[f(X)].

(3)

其中，Δ(g)是只与变换g有关的量.我们称I为相对不变量，若Δ(g)≡1，则称I为绝对不变量.

公式(3)表明，不变量I是定义在容许图像函数空间(即发生了一系列相似、仿射或者其它变换的所有图像集合)上的泛函，该泛函对变换群中的任意变换g具有不变性.图像矩不变量的构造就是寻找特定变换下的泛函I，使得I[f(g·X)]=I[f(X)].在实际应用中，为了适应图像的不完美分割、噪声以及离散化数值算法的误差等其它因素所带来的影响，对绝对不变量的定义进行弱化：I[f(X)]不应明显地与I[f(g·X)]不同.我们可以用类间离散度和类内离散度来对所构造的不变量进行评估.

接下来简要介绍构造不变量的方法.以仿射矩不变量(AMIs)的构造为例，这方面的理论研究最早源于19世纪的代数不变量理论.当然也可以采用其它数学工具.如采用归一化方法[6]来推导AMIs，其基本思想是把仿射变换分解成一些简单变换(一般分解为6个基本单参数变换)，对每个单一变化采用归一化方法来构造不变量.根据不同类型的分解和基本归一化约束可对该方法进一步进行分类.如文献[7-12]介绍的6种方法.还有其它方法，如张量方法、图论方法、求解偏微分方程[13-14](Cayley-Aronhold方程)的方法.

有关矩不变量理论研究的另一条主线就是从实数到复数域，再到四元数域，最后再上升到Clifford代数层面.矩函数在四元数及Clifford代数层面上的推广，能够使矩技术很自然地处理多通道图像(彩色图像、高光谱图像)；另外，相关研究也完善了矩不变量理论.

2 彩色图像矩不变量理论研究进展

前面我们提及的矩不变量理论都针对灰度图像，相比之下，彩色图像的矩不变量的相关研究少之又少.对于彩色图像，通常的做法是把它变为灰度图像，然后再利用已有的矩不变量理论进行处理.然而这种方法丢失了彩色图像最重要的颜色信息.另一种方法就是分通道处理，即把彩色图像的R、G和B通道看成三幅灰度图像，分别计算每一通道的矩不变量[15].

为了研究彩色图像各通道间的关系，Mindru等人在图像通道上使用一定的乘积和幂运算来计算矩，他们定义了度为d=α+β+γ的广义彩色矩[16]：

(4)

其中，R、G和B是三个颜色通道的图像函数，α、β和γ为非负整数.使用这些矩来构造仿射不变量，同时构造了仿射变换和对比度线性变化下的组合不变量.然而，这些特征具有较高的冗余性.同时，矩函数的定义中出现了过多的幂运算，这对于亮度值的非线性变换是比较敏感的，会导致误分类.

2.1 基于四元数的彩色图像矩不变量

为了把彩色图像作为一个整体并区别于分通道的方法，我们在四元数架构下系统研究了彩色图像的矩不变量理论[17-21].南京大学的陈北京等科研人员在四元数架构下也做了很多原创性的工作[22-25].首先，我们简要介绍一下四元数的概念及其表示方法.

四元数是复数的推广形式，它具有一个实部和三个虚部.

q=qr+qi·i+qj·j+qk·k.

(5)

其中，三个虚部满足如下乘法规则：

i2=j2=k2=-1,ij=-ji=k,jk=-kj=i,ki=-ik=j.

(6)

若四元数q的实部为零，称q为纯四元数.四元数的共轭为：

(7)

四元数的范数为：

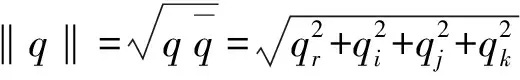
(8)

四元数的逆为：

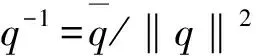
(9)

当纯四元数q的范数为1，称q为单位纯四元数.设μ为单位纯四元数，其欧拉公式为：

eμθ=cosθ+μsinθ.

(10)

对于一幅彩色图像f(x,y),把它以纯四元数的形式进行表示：

f(x,y)=fR(x,y)·i+fG(x,y)·j+fB(x,y)·k.

(11)

其中，fR(x,y)、fG(x,y)和fB(x,y)分别表示彩色图像的R、G和B三个颜色分量.x和y分别代表像素在图像矩阵中的行号和列号.这样，一幅彩色图像就被表示为一个四元数矩阵.基于四元数的彩色图像处理就是以这个四元数矩阵为研究对象，相对于传统的将颜色信息分通道的处理方法，或是将彩色图像灰度化的处理方法而言，四元数方法保留了彩色图像信息的完整性，为实际的工程应用提供了一个新的研究方法.

接下来给出我们所定义的四元数矩、四元数傅里叶-梅林矩和四元数径向矩的概念.设彩色图像f(x,y)如公式(11)所示，(m+n)阶左四元数矩定义如下：

QL(m,n)=∬R2(x-μy)m(x+μy)nf(x,y)dxdy.

(12)

右四元数矩定义如下：

QR(m,n)=∬R2f(x,y)(x-μy)m(x+μy)ndxdy.

(13)

双边四元数矩定义如下：

QT(m,n)=∬R2(x-μy)mf(x,y)(x+μy)ndxdy.

(14)

之所以四元数矩有三种定义形式，是因为四元数的乘法不满足交换律，但它们在描述彩色图像几何形变的能力上是一样的.以左四元数矩为例，我们给出了相似矩不变量：

(15)

有关仿射四元数矩不变量的构造参见文献[19].在极坐标下，我们给出了左(右)四元数径向矩的定义：

(16)

(17)

构造了基于四元数径向矩的相似和仿射矩不变量：

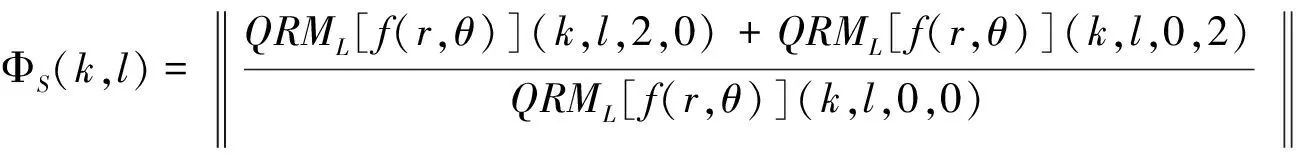
(18)

(19)

在四元数径向矩的定义中，令k=m-1,l=-n,p=0,q=0,那么四元数径向矩就退化为在文献[17]中所定义的四元数傅里叶-梅林矩：

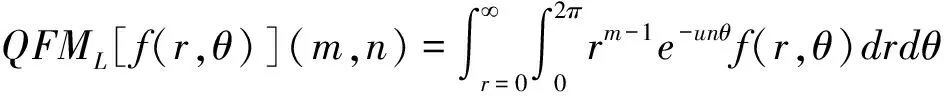
(20)

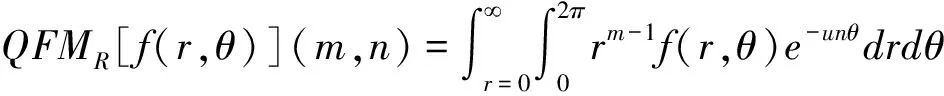
(21)

若令k=m+n+1,l=n-m,p=0,q=0,那么四元数径向矩就退化为四元数矩.

国内学者陈北京侧重于极坐标下四元数正交矩函数及其不变量的研究[22-25].他在文献中给出了四元数泽尼克矩[22]的定义，构造了该矩函数的相似不变量，并应用于目标识别中.四元数泽尼克矩定义如下：

(22)

其中，|m|≤n,n-|m|为偶数；Rn，m(r)为泽尼克多项式.由于泽尼克多项式比较复杂，在构造相似矩不变量的过程中涉及一系列推导，相关矩不变量的构造参见文献[22].

文献[23]给出了(左)四元数贝塞尔-傅里叶矩的定义：

(23)

陈北京等人在文献[24]中对几种四元数架构下的正交矩给出了统一的定义形式：

(24)

其中，由于φn,m(r)取值不同就得到了不同类型的矩函数定义，作者对比分析了四元数旋转矩、四元数径向矩、四元数傅里叶-梅林矩、四元数正交傅里叶-梅林矩、四元数泽尼克矩、四元数伪泽尼克矩，给出相应矩函数的相似不变量，并对这几种矩函数在图像重建、图像配准以及人脸识别方面的应用进行对比分析.文献[24]是对四元数正交矩的一个很好总结.

此外，黄宇等人把四元数矩应用于医学图像配准领域[26].王向阳等人提出了四元数径向调和傅里叶矩[27]的概念并应用于彩色图像检索，他们还定义了局部四元数指数矩[28]并应用于彩色图像数字水印.希腊学者Tsougenis等人分别把四元数径向切比雪夫矩和四元数径向矩应用于彩色图像数字水印方面[29-30].

矩函数的离散化算法也是很重要的研究方向.Karakasis等人针对正交多项式的特点，在四元数层面上系统研究了切比雪夫矩、Krawtchouk矩、对偶哈恩矩、勒让得矩、正交傅里叶-梅林矩、泽尼克和伪泽尼克矩，分析了这些矩函数的离散化算法，给出了相似不变量[31].应用相应的矩函数，他们实现了彩色图像重建、彩色目标分类和模版匹配.

2.2 基于Clifford代数的彩色图像矩不变量

作为四元数的推广——Clifford代数已逐渐进入科研人员的视线中，它不仅仅是数学家的研究对象，而逐步在数字信号处理、高光谱图像处理、模式识别等领域崭露头角[32].

1878年，W.K.Clifford提出Clifford代数，又名几何代数.Clifford代数结合了内积和外积两种运算，是复数、Hamilton的四元数和Grassmann的扩张代数的推广，能够进行高维的几何计算，在数学和物理学上有着广泛的应用.近年来，Clifford代数已逐渐被工程技术领域的科研人员所重视，在图像处理、计算机视觉与模式识别等领域得到了初步应用.

对于整数n,[n]={1,2,…,n}，[n]的幂集记为2[n].Clifford代数定义如下：

对于n≥1的整数，2n维代数Clp,q,(p+q=n)定义为由{ei|i=1,2,…,n}生成的结合代数.其中，e0=eφ=1∈R，ei满足如下乘法规则：

eiej=-ejei,i≠j.

(25)

(26)

Clifford代数的乘法是由2[n]的子集按字典顺序形成：

(27)

(28)

上述定义中，由集合{1,e1e2,e1e3,e2e3}生成的空间同构于四元数空间，也就是说，Clifford代数本身是四元数的高维推广，四元数是一类特殊的Clifford代数[32].

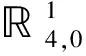
f(x,y)=fR(x,y)·e1+fG(x,y)·e2+fB(x,y)·e3+0·e4.

(29)

假设B是一个双向量，那么f(x,y)在B上的投影为：

f=f·B·B-1=(f·B+f∧B)·B-1Δf‖B+f⊥B.

(30)

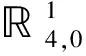
(31)

其中，B是单位双向量，在该矩函数的基础上定义了相似矩不变量.

3 未来工作展望及结论

本文给出了矩不变量的基本原理，对现有彩色图像矩不变量理论进行了简要综述.目前这方面的相关研究仍然比较活跃，有许多值得研究的方向.

第一，由四元数正交矩所构造的不变量都是相似不变量，而仿射不变量的构造比较困难.目前还没有相关文献报道，这主要是由于一些正交多项式比较复杂造成的.如何构造简单的正交多项式并以此来实现仿射不变量的构造是一个值得研究的课题.同时，需要注意的是，许多正交多项式的正交性是连续意义上的正交，在离散情况下并不正交，而我们编程必须要对连续的正交多项式进行离散化处理.因此，离散条件下的正交多项式对于不变量的稳定性及算法的有效性无疑是个重要的研究课题.

第二，在Clifford代数层面上矩不变量理论仍需进一步完善.此外，相关理论在图形、图像处理中的应用研究仍有许多可挖掘的地方.

第三，无论是四元数还是Clifford代数都不满足乘法交换律，这一点不利于程序的编写.可以考虑在乘法具有可交换性质的代数系统上推广矩不变量理论，比如缩减双四元数[34]就是一类可交换的四元数.在可交换代数系统上矩函数的定义及其不变量的构造值得深入研究.

第四，一些特殊的图像形变，如弹性变换(印刷在瓶子上的文字在图像平面上显示所表现出来的形变),弹性形变在目标识别中有着很大的实用性，在弹性形变下彩色图像矩不变量的构造如何是需要进一步探讨的问题.

[1]M.K.Hu.Visual pattern recognition by moment invariants[J].IRE Trans.Inf.Theory,1962,8(2):179-187.

[2]Y.S.Abu-Mostafa.Recognitive aspects of moment invariants[J].IEEE Trans.PAMI,1984,6(6):698-706.

[3]M.R.Teague.Image analysis via the general theory of moments[J].J.Opt.Soc.Am,1980,70(8):920-930.

[4]R.Mukundan,S.H.Ong,P.A.Lees.Image analysis by tchebichef moments[J].IEEE Trans.Image Proc.,2001,10(9): 1357-1364.

[5]Y.Sheng,H.H.Arsenault.Experiments on pattern recognition using invariant Fourier-Mellin descriptors[J]. J.Opt.Soc.Am.A,1986,3(6):771-776.

[6]I.Rothe,H.Susse,K.Voss.The method of normalization to determine invariants[J].IEEE Trans.PAMI,1996,18(4): 366-376.

[7]Y.S.Abu-Mostafa,D.Psaltis.Image normalization by complex moments[J].IEEE Trans.PAMI,1985,7(1):46-55.

[8]S.C.Pei,C.N.Lin.Image normalization for pattern recognition[J].Image and Vision Computing.,1995,13(10): 711-723.

[9]T.Suk,J.Flusser.Affine normalization of symmetric objects[C].In Proceedings of the Seventh International Conference on Advanced Concepts for Intelligent Vision Systems Acivs’05,2005:100-107.

[10]D.Shen,H.H.S.Ip.Generalized affine invariant image normalization[J].IEEE Trans.PAMI,1997,19(5):431-440.

[11]J.Sprinzak,M.Werman.Affine point matching[J].Pattern Recognition Letters,1994,15(4):337-339.

[12]J.Heikkilä.Pattern matching with affine moment descriptors[J].Pattern Recognition,2004(37):1825-1834.

[13]T.Suk,J.Flusser.Affine moment invariants generated by graph method[J].Pattern Recognition,2011(44): 2047-2056.

[14]J.Flusser,T.Suk.Pattern recognition by affine moment invariants[J].Pattern Recognition,1993,26(1):167-174.

[15]T.Suk,J.Flusser.Affine moment invariants of color images[C].In Proceedings of 13th International Conference on Computer Analysis of Images and Patterns(CAIP2009),2009:334-341.

[16]F.Mindru,T.Tuytelaars,L.V.Gool,T.Moons.Moment invariants for recognition under changing viewpoint and illumination[J].Computer Vision and Image Understanding,2004,94(1-3):3-27.

[17]L.Guo,M.Zhu.Quaternion Fourier-Mellin moment invariants for color images[J].Pattern Recognition,2011, 44(2):187-195.

[18]刘恋,刘伟宁,郭立强.彩色图像的四元数径向矩仿射不变量[J].激光与红外,2012,42(4):463-467.

[19]朱明,孙继刚,郭立强.彩色图像的四元数矩不变量研究[J].中国光学,2011,4(5):497-502.

[20]郭立强.基于四元数的彩色图像处理算法研究[D].北京:中国科学院研究生院,2011.

[21]L.Guo,M.Dai,M.Zhu.Quaternion moment and its invariants for color object classification[J].Information Sciences,2014,273:132-143.

[22]B.Chen.Quaternion Zernike moments and their invariants for color image analysis and object recognition[J]. Signal Processing,2012,92(2):308-318.

[23]Z.Shao.Quaternion Bessel-Fourier moments and their invariant descriptors for object reconstruction and recognition[J].Pattern Recognition,2014,47(2):603-611.

[24]B.Chen.Color image analysis by quaternion-type moments[J].Journal of Mathematical Imaging and Vision,2015, 51(1):124-144.

[25]陈北京,孙星明,王定成,等.基于彩色图像四元数表示的彩色人脸识别[J].自动化学报,2012,38(11):1815-1823.

[26]黄宇,华亮,冯浩,等.四元数矩理论的彩色医学图像配准[J].光电工程,2013,40(3):102-107.

[27]X.Y.Wang.Invariant quaternion radial harmonic fourier moments for color image retrieval[J].Optics & Laser Technology,2015(66):78-88.

[28]X.Y.Wang.A new robust color image watermarking using local quaternion exponent moments[J].Information Sciences,2014(277):731-754.

[29]E.D.Tsougenis.Color image watermarking via quaternion radial tchebichef moments[C].IEEE International Conference on Imaging Systems and Techniques,2013:101-105.

[30]E.D.Tsougenis.Adaptive color image watermarking by the use of quaternion image moments[J].Expert Systems with Applications,2014(41):6408-6418.

[31]E.G.Karakasis.A unified methodology for computing accurate quaternion color moments and moment invariants[J].IEEE Trans.Image Processing,2014,23(2):596-611.

[32]E.Bayro-Corrochano,G.Scheuermann.Geometric algebra computing in engineering and computer science[M].Springer Press,2010.

[33]J.Mennesson.Color fourier-mellin descriptors for image recognition[J].Pattern Recognition Letters,2014(40): 27-35.

[34]H.D.Schütte,J.Wenzel.Hypercomplex numbers in digital signal processing[C].In proc.IEEE Conf.Symp.Circuits Syst,1990(2):1557-1560.

Research Progress on Moment Invariants for Color Image

LIU Lian1, GUO Li-qiang2

(1.School of Physics and Electronic Electrical Engineering,Huaiyin Normal University, Huai’an Jiangsu 223300,China; 2. School of Computer Sciences and Technology, Huaiyin Normal University, Huai’an Jiangsu 223300,China)

The theory of moment invariants for color image is a new research area in pattern recognition. However, most of the existing theory was related to gray image, only a little paper addressed the color image. In order to draw more attention from research community about pattern recognition, and to push forward the research frontier of color image moment invariants, we give a general progress overview. A discussion about the main problems that should be solved in color image moment invariants and the future work in this area are given. This paper should provide some help for the research community on image moment invariants and its applications.

color image; moments; moment invariants

2016-09-04

国家自然科学基金项目“基于可交换Clifford代数的彩色图像矩不变量研究”(61203242)；江苏省自然科学基金项目“可交换Clifford代数神经网络及其应用”(BK20141253)。

刘 恋(1986- )，女，助理实验师，硕士，从事图像处理、目标识别与跟踪研究。

郭立强(1982- )，男，副教授，博士，从事图像处理、计算机视觉与模式识别研究。

TP391.4

A

2095-7602(2016)12-0017-07