BPSK信号在Nakagami衰落信道下误码性能分析

孙蔓，徐荣蓉，孙得娣，张佩佩

BPSK信号在Nakagami衰落信道下误码性能分析

孙蔓，徐荣蓉，孙得娣，张佩佩

首先介绍了BPSK信号调制与解调的基本原理以及Nakagami衰落信道的统计特性；随后重点分析、推导了BPSK信号在通过Nakagami衰落信道后，经相干解调的平均误码率理论闭型表达式；最后在Matlab仿真平台中对该误码率闭型表达式进行了仿真验证，并总结了BPSK调制在Nakagami衰落信道中的误码性能。

BPSK；Nakagami信道；Matlab仿真；误码率

0 引言

在实际的通信信道中，大多数信道具有带通传输特性，而数字基带信号不能直接在这种带通传输特性的信道中传输。所以，必须用数字基带信号对载波进行调制。与模拟通信系统相比，数字调制和解调同样是通过某种方式，将基带信号的频谱由一个频率位置搬移到另一个频率位置上去。而数字调制的基带信号不是模拟信号而是数字信号，数字调制是利用数字信号的离散值去键控载波。用数字基带信号改变正弦载波的幅度、频率或相位中的某个参数而产生相应的数字振幅调制、数字频率调制和数字相位调制。因此，在二进制数字调制中，当正弦载波的相位随二进制数字基带信号离散变化时则产生二进制移相键控信号，即BPSK信号。通过研究BPSK信号在Nakagami衰落信道下的误码率，从而得到衰落信号统计的特性对系统性能分析提供相应的依据。

1 BPSK信号的数学原理

1.1 BPSK信号调制原理

在数字信号经通信信道传输时，由于调制器是接口器件，其将数字信息映射成与信道特性相匹配的模拟波形。一般先从信息序列｛an｝一次提取k=log2M个二进制数字形成分组，再从M=2k个确定的有限能量波形｛sm（t）, m=1,2,...,M｝中选择其中之一送往信道进行传输。当序列｛an｝到波形｛sm（t）｝的映射没有受到先前发送波形的约束时，这种调制器称为无记忆的；而在任意时间间隔发送的波形决定于一个或多个先前发送波形的约束时，这种调制器就称为有记忆的。在数字通信系统中，调制器将二进制数字序列映射成一组相应的信号波形，这些波形的差别在于幅度、相位、频率或者两个或多个信号参数的组合。其中，数字相位调制通常被称为相移键控(PSK)。在采用无记忆调制方式的情况下，假定在调制器输入端的二进制数字序列的速度均为Rb/s，那么在数字相位调制中，M个信号波形[2]可表示为公式（1）：

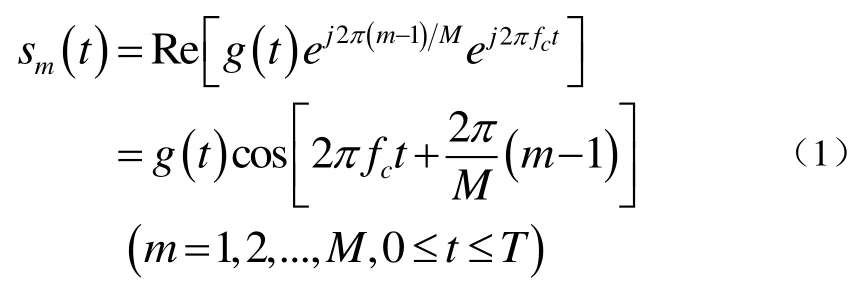
上式中，g（t）是信号脉冲波形，其形状影响发送信号的谱；而θm=2π（m-1）M是载波的M个可能的相位用于传送发送信息；时间间隔T=k R称为符号间隔。这些信号波形具有相等的能量，即公式（2）：

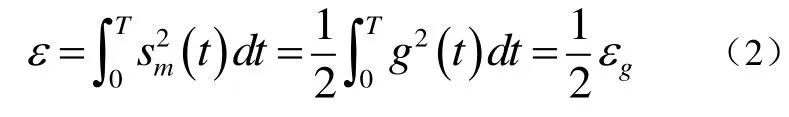
其中，εg表示脉冲g（t）的能量。

该M个信号波形可以表示为具有单位能量的两个标准正交信号波形f1（t）和f2（t）的线性组合，即式（3）：

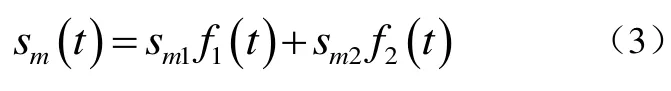
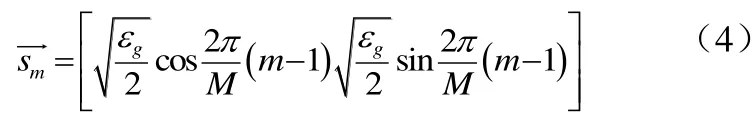
当M=2,4,8时该信号分别表示为 BPSK、QPSK和8PSK。并且当M=2时，其相当于一维信号，与二进制数字脉冲幅度调制(PAM)信号相同。其中，数字PAM信号波形一般表示为式（5）：

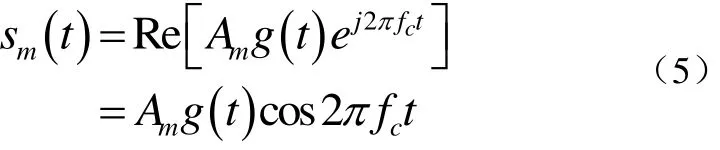
其中，Am表示M个可能的幅度，相应于M=2k个可能的k比特组或符号。信号幅度Am取离散值（电平）为式（6）：

上式中，d是相邻信号幅度之间的距离。所以在M=2的情况下，二进制PAM波形具有特殊性质，即式（7）：

所以，该两个信号具有相等的能量且互相关系数为-1，其被称为双极性信号。

1.2 BPSK信号解调原理

在发送端的调制器将数字序列映射成信号波形后通过信道传输时，该信号会受到信道高斯噪声相加的影响。假定信道以加性高斯白噪声(AWGN)来恶化信号，那么在0≤t≤T间隔内，接收信号可以表示为式（8）：

其中，n（t） 表示具有功率密度谱Φ（f）=N02（W/Hz）的加性高斯白噪声的样本函数。通过对r（t）在信号间隔时间上经过接收机使错误概率最小使系统达到最佳。一般可将接收机分为两个部分即信号解调和检测器，如图1所示：

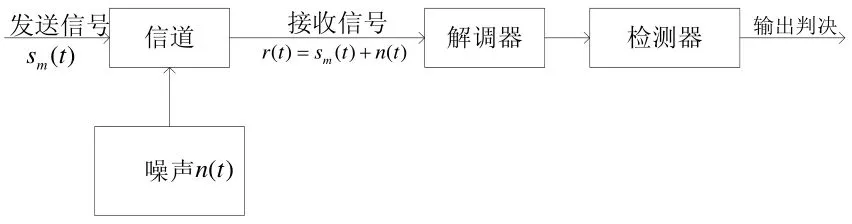
图1 BPSK信号解调原理图

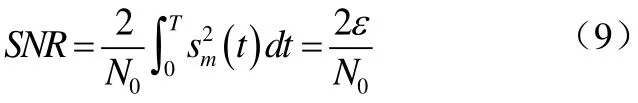
上式表明匹配滤波器的输出信噪比决定于信号波形sm（t）的能量。

对于BPSK信号在AWGN信道下在进行无记忆调制时，基于最大似然准则（ML）的判决规则进行判决，该二进制双极性信号的平均错误概率[2]是式（10）：

其中，ε/N0称为比特信噪比。

2 Nakagami衰落统计特性

在移动无线信道中，瑞利分布和莱斯分布都能很好的对信号通过衰落信道后的包络进行建模。但是，在实际的无线环境中，Nakagami分布能够与测试结果更加匹配吻合[3]。在Nakagami衰落信道下，系统传输的符号的包络受到的衰落幅度α服从Nakagami分布即m分布，其概率密度函数为式（11）：

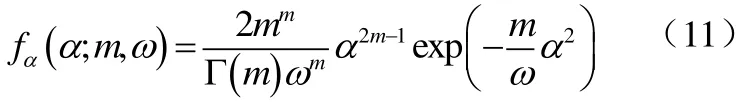
其中，m和ω是Nakagami分布的两个重要参数，表达式为式（12）：

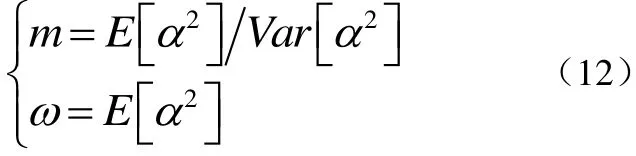
其中，E［·］表示求均值，Var［·］表示方差。ω是衰落幅度α的均方值，m被称为形状因子或衰落指数，表示此时小尺度衰落的严重程度，其取值满足m≥1/2。Γ（·）表示伽马函数并定义为式（13）：

其中，对衰落指数m的不同取值存在几种特殊情况。

为了进行统一对比，所有曲线对应的ω取值都为1，如图2所示：

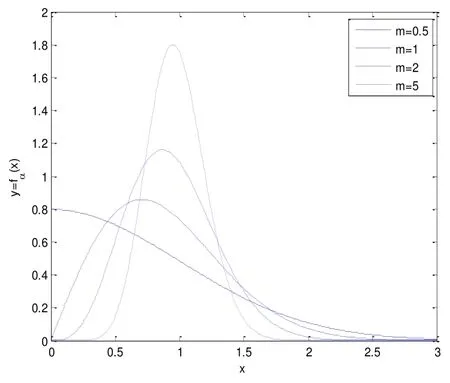
图2 Nakagami分布的概率密度函数曲线图

从图中可以看出，m取值越大，概率密度函数曲线越陡峭，即对应的方差越小，衰落越轻微。当m取值趋向于无穷大时，其概率密度函数演变为Dirac冲击函数，此时以概率1取得均值，方差为0，信道中不存在小尺度衰落。综上所述，当衰落参数m的取值变化时，Nakagami衰落信道的衰落严重程度也会随之变化。并且当m取特定数值时，Nakagami衰落信道模型能够有效地涵盖现有的经典衰落信道模型，具有很强的通用性。

根据文献[4]假设Nakagami衰落信道当中存在加性高斯白噪声，其功率谱密度为N0，发送端发送功率为E，接收端瞬时接收信噪比记为γ，每个符号对应的平均接收信噪比记作，则两者表达式分别为式（14）：

通过单个符号的瞬时接收信噪比γ的概率密度函数和单个符号包络受到的衰落幅度α的概率密度函数的两者关系可得在Nakagami衰落信道下，接收端接收到单个符号的信噪比γ的概率密度函数表达式为式（15）：

3 BPSK在Nakagami衰落信道下理论平均误码率推导

BPSK信号序列产生之后，其会被传送到信道中。而实际的信道是一个充满各种干扰的环境，所以调制后的信号不可能在信道中不受干扰影响的直接进行传输。一般的信道干扰包括乘性干扰和加性干扰，其中乘性干扰是伴随信号的存在而存在、消失而消失的，加性干扰是不管有没有传送信号始终存在信道所固有的干扰。所以 BPSK信号在经过Nakagami信道时受到乘性干扰，同时为更加逼真的去模拟这样的调制信号的传输环境，所以在经过该衰落的序列中随机叠加不同信噪比的高斯白噪声。

由于频率非选择性信道会导致发送信号的乘性失真，信道慢衰落的条件要求至少在一个信号传输间隔内将乘法过程看做是一个常数。所以假设信道衰落足够慢以致相移是能够从接收信号中无误差的被估计出，这种情况便能够实现接收信号的理想的相干检测。对BPSK采用一个匹配滤波器处理接收信号，通过计算判决变量并依据其确定差错率确定该通信系统的性能。根据前面所述BPSK信号的解调原理可知对于某一固定衰减α，其接收端接收到的单个符号的信噪比γ函数的BPSK差错率为式（16）：

上式中，γ=α2ε/N；Q（·）是一种经常用来表示高斯

0 PDF尾部曲线下的面积的函数，定义为式（17）：

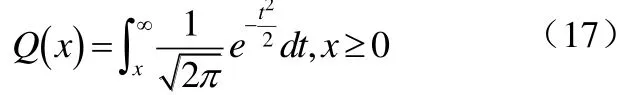
上式的 BPSK差错率是在条件衰减α固定不变的情况下得出的。所以为了得到随衰减α随机变化时的差错率，可将Pγ（γ）对变量γ的概率密度函数求平均，即计算如下的积分式（18）：

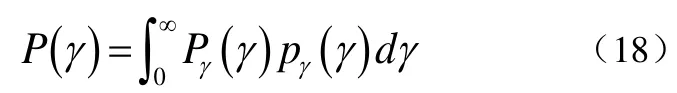
其中，pγ（γ）是衰减α随机变化时信噪比γ的概率密度函数。所以BPSK在Nakagami衰落信道下误码率的计算表达式为式（19）：

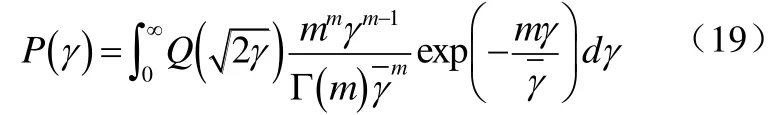
其中，Q（·）还可以写成另一种表达形式[4]即式（20）：

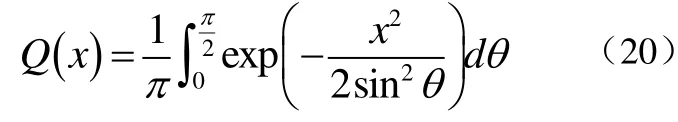
所以，将公式（20）运用到公式（19）中可得式（21）：

在公式（21）的推导中，用到了矩生成函数（MGF，The moment generating function）。其定义为式（22）：

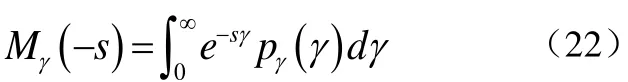
对于Nakagami衰落信道的接收端接收到单个符号的信噪比γ的概率密度函数而言，其矩生成函数可以化简[4]写成式（23）：

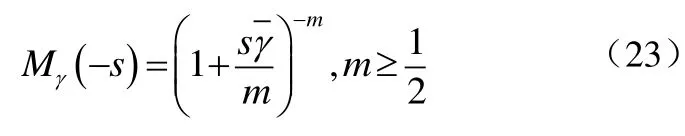
根据公式（23），公式（21）可以化为式（24）：

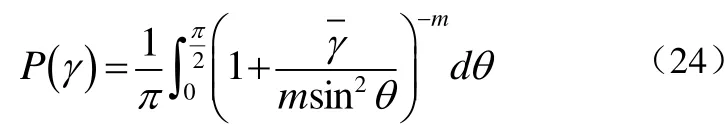
其中，2F1（·,·;·;·）为Gauss hyper-geometric函数[5]，其定义为式（26）：

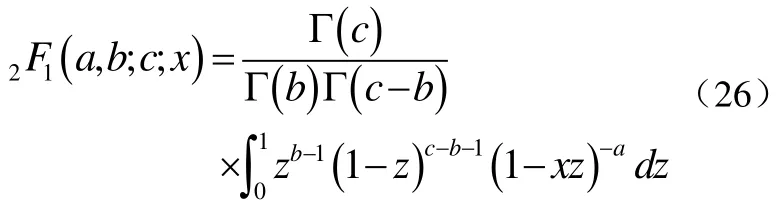
通过进行上述系列的数学的变量代换和变形便可得到BPSK信号在经过Nakagami衰落信道后的误码率的一个闭合式的解。相较于原来的无穷积分表达式，该闭合式不仅更好的反映了误码率同接收信噪比和衰落指数的关系而且有利于计算和分析，使得仿真更加方便精确。

由于上式所得误码率是对一般的衰落指数m≥1/2适用的，而当m无限趋近于无穷大时，依据Nakagami信道在接收端接收到的单个符号信噪比的概率密γ度表达式可知其成为了Dirac冲击函数即接收到的信噪比γ以无限大的概率出现在均值点没有衰落，相当于Nakagami衰落信道对信号所产生的乘性干扰为 1即其是一个无衰落的信道。所以此时BPSK信号在经过Nakagami信道后，接收端接收到的信号实际上等效为一个叠加了高斯白噪声的原始的发送信号。根据 BPSK信号在通过具有高斯白噪声的信道后其接收到的信号的概率密度函数和判决法则等可得m→∞时，BPSK信号的误码率[1]的表达式为式（27）：

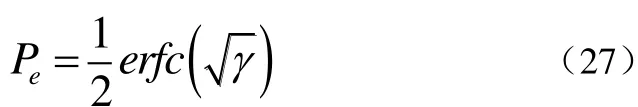
其中，erfc（·）为高斯误差函数[6]，其定义为式（28）：

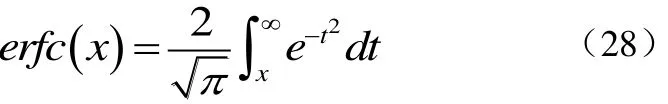
4 仿真及结果分析

基于前面的数学原理，利用MATALB进行仿真并分析数学理想模型建立的合理性。根据BPSK信号在Nakagami衰落信道下误码率的计算表达式可知该信号的误码率不仅与Nakagami分布的衰减指数m有关，还与其每个符号对应的平均接收信噪比γ有关。对于不同的衰减指数m赋予不同的数值即做不同的变化，同时对该信道中的平均信噪比从0db到40db不断地进行变化，这样便可得到在不同的衰减指数m和平均信噪比γ情况下的BPSK信号的误码率。并且对原始信号的误码率取对数得到误码率与衰减指数m和平均信噪比的关系的仿真图如图3所示：

图3 BPSK在Nakagami衰落信道下误码率的理论仿真图

从而便于分析BPSK信号在经过Nakagami衰落信道后的系统性能。

图中蓝色实线描绘的是通过超几何函数公式（25）和误差函数公式（27）所表示的BPSK误码率的理论计算值；而红色原点和方块所描绘的则是通过无穷积分公式（19）所表示的BPSK误码率的基准理论仿真值。这两类曲线的良好重合性证明了本文所推导得到的Nakagami衰落信道下BPSK理论平均误码率公式的正确性。从上述的BPSK误码率的仿真图可以看出，BPSK信号m的误码率与平均信噪比及衰落指数息息相关：当衰落指数m为一固定值时，接收的平均信噪比越大，BPSK信号的误码率越低；而当平均信噪比为一固定值m时，BPSK信号的误码率随着Nakagami信道的衰落指数m的增大而减小，即m越大时误码m率越小。所以当m逐渐增大时，系统性能将得到改善，当m为无穷时，系统性能趋于无衰落的高斯信道。

6 总结

本文在简要介绍了 BPSK信号的调制与解调原理和Nakagami衰落信道的统计特性后，推导了Nakagmi衰落信道下，BPSK经相干解调和最大似然判决输出的统计平均误码率理论闭型表达式，并进行了计算机仿真验证。仿真显示，BPSK信号的误码率与Nakagami衰落信道的衰落指数和接收端每个符号的平均信噪比有关，通过合理的选择这两个参数可使得误码率最低、系统性能达到最好。

[1] 樊昌信.通信原理(第六版)[M].北京：国防工业出版社, 2008.

[2] John G.Proakis著,张力军等译.数字通信(第四版)[M].北京电子工业出版社, 2003,1.

[3] Nakagami M. The m-distribution: A general formula of intensity distribution of rapid fading[J].Statistical Method of Radio Propagation,1960.

[4] M.K. Simon and M.-S. Alouini. Digital communication over fading channels,2nd ed.[M].New York:Wiley,2005.

[5] A. Erdelyi. Higher Transcendental Functions[M]. New York: McGraw-Hill.1953.Vol.1.

[6] S.Gradshteyn, I.M.Ryzhik. Table of Integrals. Series and products(7th ed.)[M].San Diego: Academic Press,2007.

Analysis of BER Performance of BPSK Modulation over Nakagami Fading Channel

Sun Man, Xu Rongrong, Sun Dedi, Zhang Peipei
(College of Computer and Information, Hohai University, Nanjing 211100,China)

This paper firstly introduces the basic principls of BPSK signal modulation and demodulation, and the statistical characteristics of Nakagami fading channel. Then it focuses on the analysis and derivation of the BPSK signal in the Nakagami fading channel through the coherent demodulation of the average error rate theoretical closed form expression. Finally, the error rate closed form expression is simulated in the Matlab simulation platform, and the BER performance of BPSK modulation in Nakagami fading channel is summarized.

BPSK; Nakagami Channel; Matlab Simulation; BER

TP393

A

1007-757X(2016)09-0071-04

2016.01.15）

孙 蔓（1995-），女，河海大学，计算机与信息学院，硕士研究生，研究方向：MIMO系统及多天线技术，南京 211100徐荣蓉（1992-），女，河海大学，计算机与信息学院，硕士研究生，研究方向：现代无线通信系统，南京 211100孙得娣（1992-），女，河海大学，计算机与信息学院，硕士研究生，研究方向：无线通信网络与MIMO系统，南京 211100张佩佩（1992-），女，河海大学，计算机与信息学院，硕士研究生，研究方向：新一代MIMO无线通信系统，南京 211100