超高堆石坝分层填筑的颗粒流模拟

黄小波

（永州市水利水电勘测设计院　永州市　425000）

超高堆石坝分层填筑的颗粒流模拟

黄小波

（永州市水利水电勘测设计院永州市425000）

针对当前堆石坝发展趋势及坝体变形预测方法的不足，研究了细观颗粒流方法用于模拟超高堆石坝应力变形特征的可行性。首先，利用FISH语言二次开发，实现在复杂边界区域快速建立密实的堆石料模型，并充分体现堆石料的级配及破碎效应；然后，以水布垭面板工程为例，基于该建模方法对超高堆石坝的填筑过程进行仿真模拟。结果表明，颗粒流模型的坝体变形与坝体实测变形比较接近。由此可见，颗粒流方法应用于模拟超高堆石坝分层分期填筑等大尺度复杂边界问题是切实可行的，从而为超高堆石坝变形预测提供新的途径。

超高堆石坝颗粒流分层填筑

引言

20世纪以来，国际上相继开工建设了一批200 m级的高面板堆石坝，取得了宝贵的经验，但从已建成工程的初步运行状况来看，这些高坝也出现了一些问题，反映了高堆石坝的新特征。目前，我国面板堆石坝的发展面临着从200 m级高坝向300 m级超高坝的突破，对于300 m级超高堆石坝，其运行特性不可能简单地通过对已建工程的观测数据进行适当外推而得到，而必须对现有的设计准则和计算方法进行调整，以适应超高坝的实际情况。

变形控制是面板堆石坝设计阶段最重要的考虑因素，对于300 m级的超高堆石坝，坝体堆石的变形控制将是决定其在技术上是否可行的关键因素。目前，基于有限元方法的数值模拟是预测堆石坝变形量的主要手段，然而，有限元方法虽然能够定性地得到坝体和面板的应力变形规律，但是计算结果尚不能达到定量分析的精度，这主要是由于堆石体是一种典型的不连续介质，在荷载作用下，堆石料会出现破碎、滑移及充填，表现出非常复杂的细观力学特性，而连续介质力学方法只能从宏观层面计算坝体的应力变形，难以反映堆石料的上述细观力学特性，计算结果往往与坝料的真实变形存在较大差距。

近些年来，离散元方法的提出和发展，为从细观层面研究堆石坝的应力变形特征提供了新的思路与方法。但是,从目前的发展现状来看，在堆石坝的模拟方面，离散元方法还仅仅只是用于研究坝料特性、碾压及流变的模拟，研究对象主要是针对小尺度的物理试样或低坝的简单模拟，而对于高堆石坝的分层填筑等大尺度复杂工程问题，尚未进行深入研究。

对离散元方法而言，计算效率是制约其工程应用的重要因素之一，随机多边形模型虽能较为真实地反映堆石料的几何特性，但是接触识别十分复杂，严重影响计算效率，而颗粒流方法将颗粒简化为圆形，接触识别简单，计算效率相对较高，这是本文采用颗粒流程序的重要原因。另外，计算过程中采用多核并行算法，模型的计算效率将进一步提高。因此,本文拟采用颗粒流程序PFC2D对超高堆石坝分层分区填筑模拟的可行性进行研究，从细观层面对超高堆石坝的宏观变形特性进行初步探索。

1　超高堆石坝分层填筑颗粒流模拟的基本原理

本文利用二维颗粒流方法对超高堆石坝的填筑进行模拟，重点在于实现坝体的分区分层填筑过程，目前暂不考虑坝体碾压及流变效应。为了实现这一目的，首先需建立堆石料的颗粒流模拟方法，并充分考虑堆石料的复杂特性，然后，基于该方法建立填筑层模型，并最终实现坝体全断面的填筑。

1.1堆石体模型的颗粒流建模方法

实验研究表明，堆石体具有明显的级配特性，几何形状为随机不规则的多面体，在一定荷载作用下会出现破裂。本文利用FISH语言二次开发，提出了一种建立堆石料颗粒流模型的方法，在模型区域内快速生成颗粒，并同时综合考虑堆石料的级配、随机形状及破碎效应，主要建模步骤如下所示：

（1）根据颗粒级配在模型区域内生成初始模型，并设置一个合适的粒径d，将级配中粒径超过d的粒料分为粗粒料，小于d的粒料分为细粒料，记录初始模型中所有粗粒料的位置及半径，并删除全部颗粒。

（2）按照级配中细粒料及其相对含量在模型区域内再次生成颗粒模型。

（3）根据（1）中记录的粗粒料形心坐标和粒径，在（2）中生成的计算模型里确定对应的区域，将落入该区域的颗粒粘结在一起，构成颗粒簇，并赋予模型细观力学参数。

图1是按照根据上述方法建立的堆石料的颗粒流模型，其中黄色颗粒为细粒料，不可破碎，蓝色颗粒为粗粒料，在一定应力条件下可发生破碎。

图1　堆石料颗粒流模型

模型中粗粒料由若干彼此相邻的细颗粒粘结在一起构成，图2为模型中随机选取的几种不同形状的粗粒料。

图2中，红圈表示初始模型中记录的粗粒料位置，黄线表示颗粒簇内部的平行粘结，相邻颗粒簇间的接触为线性无粘结接触。

图2　粗粒料的随机构成

上述颗粒流模型中，粗粒料的等效粒径按照如下式进行计算：

式中n——构成某粗粒料的细颗粒数量；

ri——细颗粒的粒径。

可以看出，该式按照面积等效的原则可以较为方便地计算得到颗粒簇的等效粒径，但是没有考虑颗粒簇内部的空隙面积，计算得到的颗粒簇的等效粒径比实际粒径偏小，由此得到的级配曲线中细粒料的含量会偏大。若忽略这一误差，在截断物理试样级配细小粒径的条件下，按照上述建模方法，数值模型的级配和物理试样的级配是十分接近的，如图3所示。

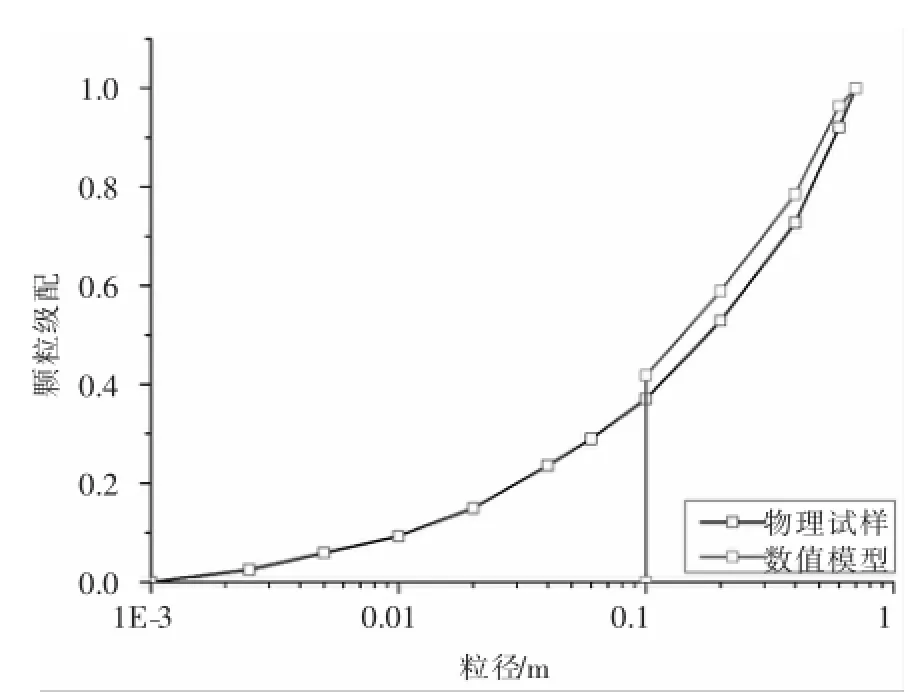
图3　堆石体颗粒流模型的粒料级配

可以看出，通过上述建模方法，可基本保证数值模型的级配与坝料真实级配一致，并且粗粒料可发生破碎，充分体现了坝料的破碎效应。虽然模型中粗粒料的形状与坝料真实形状存在一定差异，但是该建模方法不需要定义粗粒料的形状，也避免了粗粒料初始位置的搜索与判别，极大地简化了建模过程，这对于实现超高堆石坝分层分区填筑过程的模拟，具有十分重要的意义。

1.2二维颗粒流模型的细观特性

与三维模型相比，二维模型相对更加密实，且在垂直模型平面方向不受力或位移约束，这就使得二维模型的宏观力学特性与三维模型相比存在较大差异。为了使二维模型能够表现出与三维模型基本一致的力学特性，需要对二维颗粒流模型的细观特性进行修改。

（1）孔隙率。由上可知，在相同条件下，二维模型模型相对更加密实，在荷载作用下易表现出过量的剪胀现象，难以较为真实的反映三维模型的体积变形特性，因此在建立二维颗粒流模型时，需要提高模型的孔隙率，以增强模型的可压缩性。但是，若在初始建模时将模型的孔隙率设置得过大，会导致颗粒间接触不良，或无法填满整个模型区域，因此，本文所采取的方法是：首先，在生成颗粒时孔隙率取合适值，使颗粒充满模型区域，又不至于使得颗粒间重叠量过大；然后，赋予颗粒接触细观力学参数，使得模型构成一个稳定的受力体系；最后，随机删除模型中的部分细小颗粒，提高模型的孔隙率。

（2）颗粒转动特性。颗粒流方法将颗粒简化为理想的圆形，降低了颗粒间的咬合作用，对于二维颗粒流模型而言，由于缺少中间主应力方向的约束，颗粒的咬合作用进一步降低，因此在加载条件下，颗粒出现过量的转动，使得模型宏观上表现出明显的应变软化现象，这与三维堆石料模型的应变硬化特性不符。目前，在基于二维颗粒流模型模拟堆石料力学特性的研究成果中，为了解决这一问题，一种方法是将增强基本颗粒几何形状的复杂性，另一种方法是在接触关系中赋予颗粒抗转特性[16]。显然，后者建模过程更加方便，更是适合于模拟超高堆石坝分层填筑等复杂边界问题。

1.3填筑层的模拟方法

分层填筑中一个难点是分层填筑过程的处理问题。基于颗粒流方法模拟坝体分层填筑时，首先需以填筑层轮廓为边界生成墙体（walls），构建封闭的区域，然后在该封闭区域内生成颗粒，这就意味着，在填筑层中生成颗粒时，填筑层的边界必须是已知的。但是实际上，在填筑层区域生成颗粒后，经过碾压和重力作用，该填筑层会发生一定程度的沉降和侧向变形，变形后填筑层的轮廓与其初始轮廓示意图如图4所示。由图4可知，填筑层1碾压沉降至稳定状态后，其顶部实际高程与设计高程间存在高度差。在模拟后续填筑层2时，在碾压及自重作用下，填筑层2中的颗粒会首先将该高度差的区域填满，同时加上自身的压缩变形，填筑层2碾压沉降至稳定状态后，其顶部实际高程与设计高程间会形成更加明显的高度差，进而对后续的填筑层产生更加显著的影响。由此，在利用颗粒流程序模拟坝体分层填筑时，必须使得各填筑层碾压沉降至稳定状态后，其轮廓恰好与设计轮廓重合。

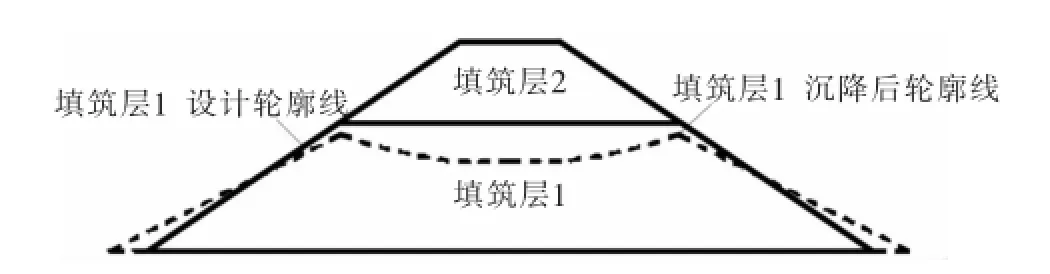
图4　填筑层变形示意图

为了满足这一要求，本文提出了一种解决方法，即在模拟填筑层1时，在设计厚度的基础之上增加一定厚度，以弥补该填筑层由于碾压及自重而引起的压缩变形，同时对上下游坡面施加法向约束；待填筑层沉降至稳定状态后，将该填筑层顶部设计高程以上颗粒全部删除，并解除上下坡面的法向约束。

由于加高层的厚度远小于填筑层厚度，当删除设计轮廓线以上颗粒及解除坡面法向约束时，填筑层内会发生一定程度的卸荷，但卸荷量很小，可以忽略填筑层边界由于卸荷而发生的改变。1.4蓄水作用的模拟方式

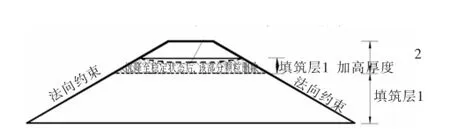
图5　堆石坝填筑层的颗粒流模拟方法示意图

超高面板堆石坝在蓄水时，在面板运行状态良好的情况下，上游水头基本以面力形式作用在面板上，并传递给坝体。因此本文在考虑蓄水作用时，将水压力作为面力进行考虑。

假定上游水面高程为H，上游坡脚为α，对于面板上游面任意颗粒，设其半径为R，形心坐标（x,y），厚度为t，则作用在该颗粒上的等效水压力为：

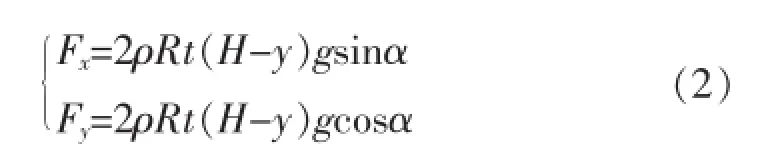
2　超高堆石坝分层分区填筑的颗粒流模拟

基于上述基本方法与原理，本文以水布垭面板堆石坝为例，对颗粒流方法在超高堆石坝分层分期填筑模拟上的可行性进行研究。首先，通过对主、次堆石料的压缩试验进行仿真模拟，通过反演获取坝料的细观力学参数；然后，结合坝体施工的实际过程，利用颗粒流程序对坝体填筑过程进行仿真模拟，并将坝体的变形结果与实测资料及有限元方法进行对比，以验证颗粒流方法在模拟超高堆石坝分层分区填筑问题上的有效性。

2.1坝料细观力学参数的反演

颗粒流模型的宏细观参数间不存在明确的对应关系，通常只能通过反演来确定与坝料宏观特性相适应的细观力学参数。本文中，通过对水布垭主、次堆石料的压缩试验进行仿真模拟，并通过反演的方式确定了坝料的细观力学参数，如表1所示。

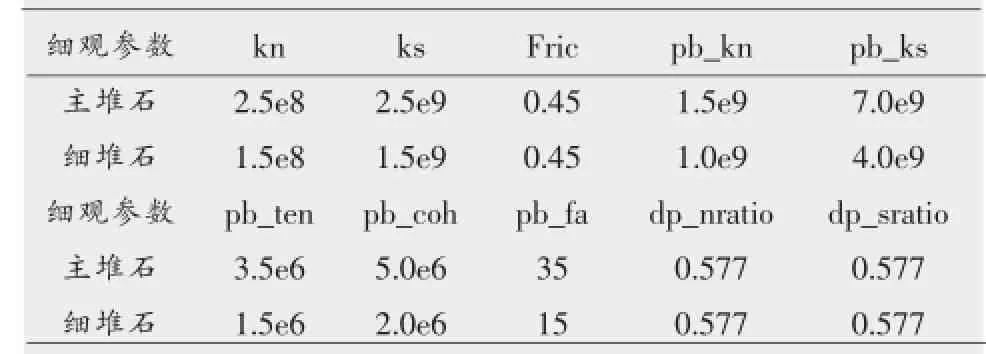
表1　水布垭堆石料细观力学参数

表中各变量的物理含义：kn，线性接触法向刚度，（N/m）；ks，线性接触切向刚度，（N/m）；fric，细观摩擦系数；pb_kn，平行连接法向刚度，（Pa/m）；pb_ks，平行连接切向刚度,（Pa/m）；pb_ten，细观抗拉强度，（Pa）；pb_coh，细观粘聚力，（Pa）；pb_fa，细观摩擦角，（°）；dp_nratio，法向临界阻尼系数；dp_sratio，切向临界阻尼系数。

按照上述细观力学参数，主、次堆石料的宏观应力变形关系如图6所示。

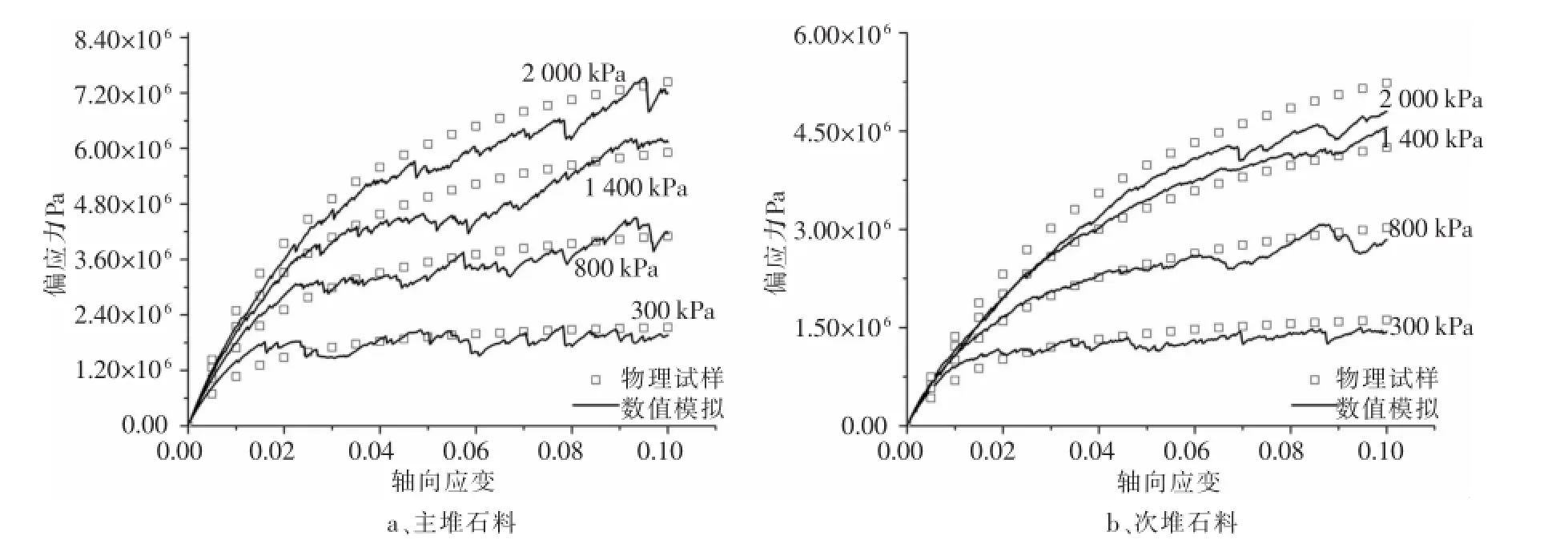
图6　堆石料颗粒流模型宏观应力应变关系

同时根据设计资料，水布垭堆石料的干密度为2 160 kg/m3，由于颗粒流模型的初始孔隙率为0.20，因此颗粒的密度取2 700 kg/m3。

2.2计算剖面及加载过程

水布垭面板堆石坝坝体最大剖面如图7所示，根据坝体的施工组织设计，填筑过程的载荷分级如表2所示。

3　颗粒流模拟结果及分析

按照图7和表2所示的加载过程，运用颗粒流方法对水布垭面板堆石坝的分层填筑过程进行模拟，可得到不同工况下坝体的宏观应力变形结果及细观变化过程。坝体填筑完成后，模型中颗粒数量为378 066。

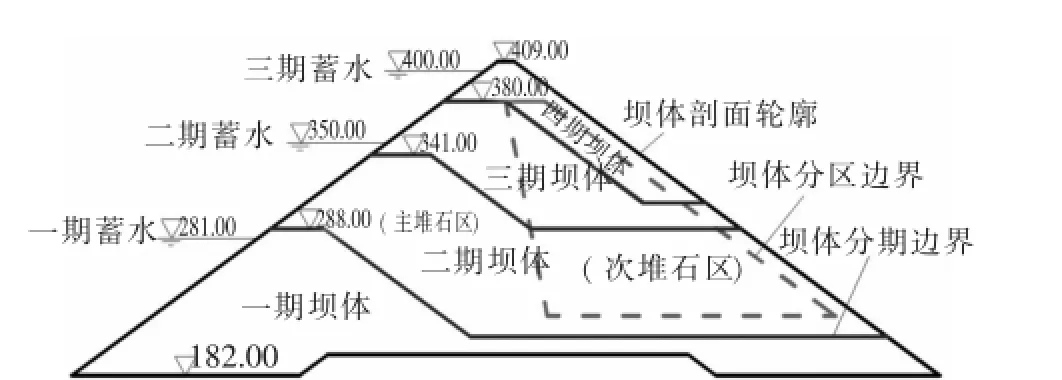
图7　水布垭面板堆石坝坝体分区及加载过程

3.1坝体变形

根据模拟结果，在不同的填筑工期，坝体的沉降位移分布如图8、图9所示。

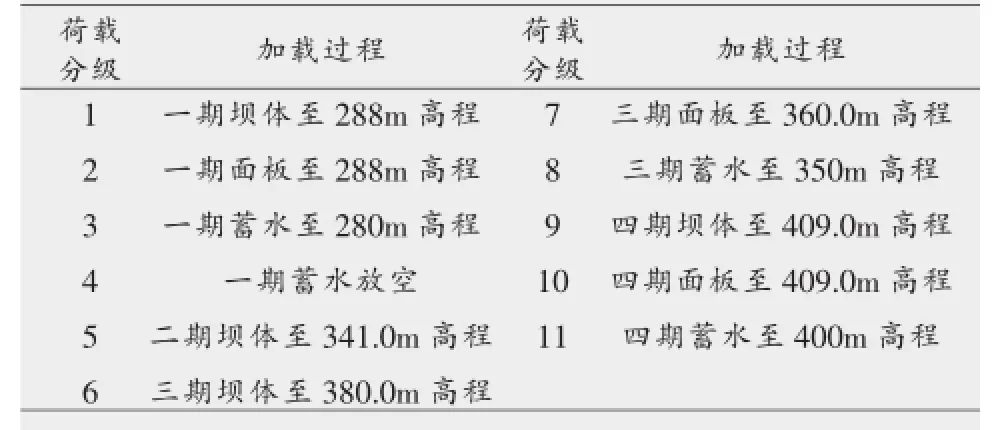
表2　颗粒流模型仿真计算荷载及加载过程

从图可以看出，坝体竣工后坝体沉降主要发生在次堆石区，主堆石区变形量相对较小。竣工期坝体最大沉降量约2.11 m，蓄水期坝体最大沉降量约2.24 m，均发生在坝轴线偏下游约305 m高程处。

3.2坝体受力

堆石体表现出复杂的力学特性，其主要原因就是内部力链网络的复杂演化特性，图10、图11反映了不同工况下坝体内部堆石料间接触力分布。

图8　一期坝体填筑及蓄水工况下坝体沉降

图9　三期坝体填筑及蓄水工况下坝体沉降

图10　四期坝体填筑及蓄水工况下坝体沉降

由图可以看出，坝体内部力链网络中，强力链主要分布在坝轴线上游主堆石区内，而次堆石区内部的接触力则相对较弱，同时，坝体蓄水后，上游坝坡附近堆石料间的接触力强度明显上升。

为便于与有限元结果进行比较，可将坝体内部颗粒间的接触力转换为颗粒集合体的等效平均应力，该转换过程可通过测量圆实现。通过在模型中设置大量测量圆，测量圆的相对尺寸为20～33.2倍颗粒平均粒径，于是可得到测量圆内颗粒集合体的平均应力分量，并合成主应力。通过计算，坝体内部的主应力分布如图12、图13所示。

图中纵坐标为高程（m），应力单位MPa。从图中可以看出，竣工期坝体最大主应力3.8 MPa，最小主应力1.0 MPa；蓄水期坝体最大主应力4.0 MPa，最小主应力1.1 MPa。蓄水后，坝体上游坡面主应力明显升高。3.3模拟结果比较及分析

“九五”公关期间，多家单位运用不同模型对水布垭面板堆石坝的宏观应力变形进行了分析计算，得出的结果如表3所示。

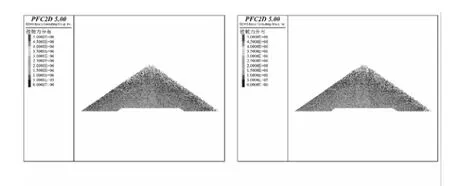
图11　坝体内部堆石料间接触力分布(N)

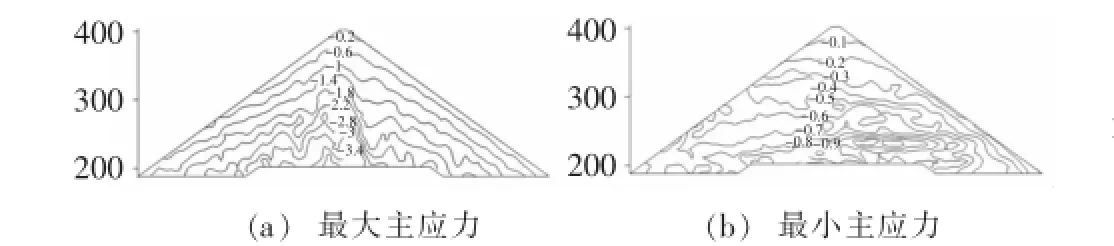
图12　竣工期坝体内部主应力分布

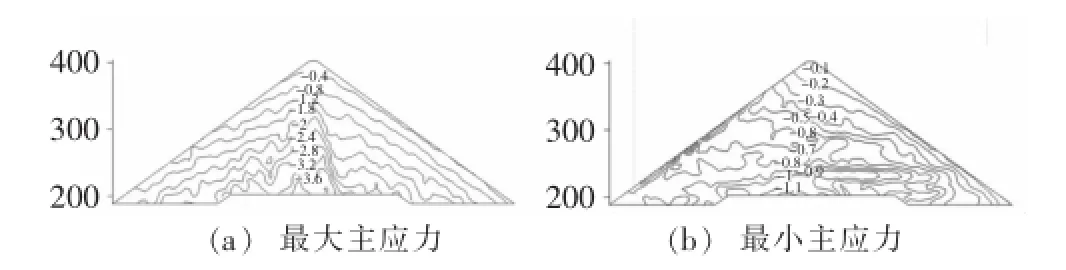
图13　蓄水期坝体内部主应力分布

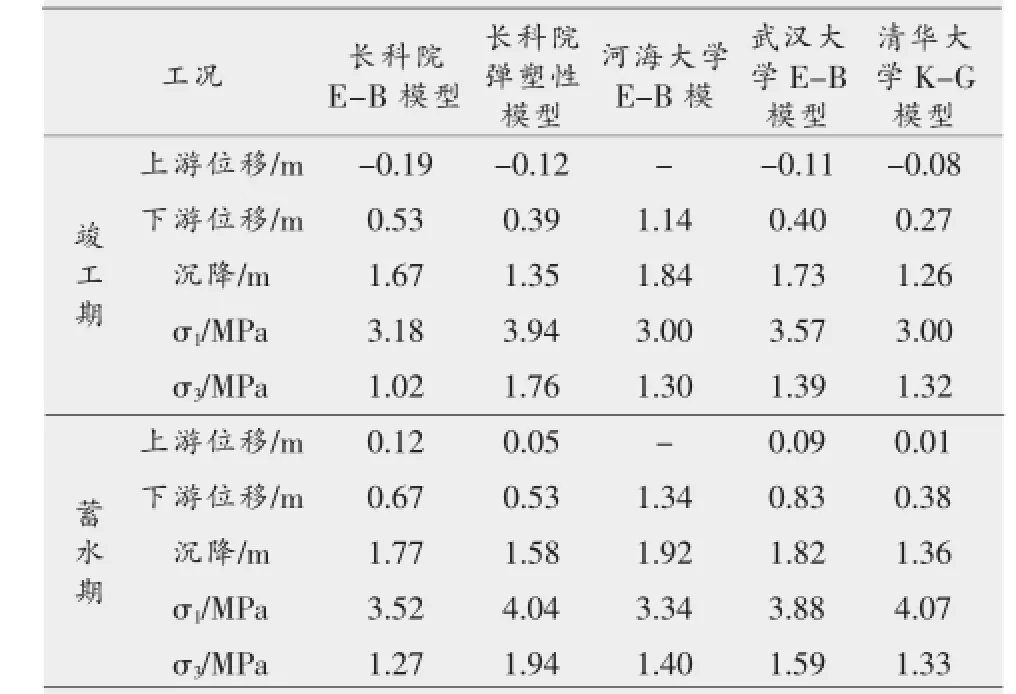
表3　不同模型三维有限元计算坝体变形应力最大值表[19]

同时，汪明元等采用“南水”双屈服面弹塑性模型对坝体填筑蓄水过程进行了模拟，得到蓄水期最大沉降约2.0 m，最大水平位移约0.50 m；清华大学错误!未找到引用源。基于修正K-G模型反馈参数计算得到蓄水期坝体最大沉降约2.39 m，最大水平位移0.55 m。

根据水布垭面板堆石坝观测结果[19]，坝体内部最大沉降约为2.45 m，发生在最大断面坝轴线偏下游侧高程300.0 m处，最大水平位移约0.47 m，发生在坝轴线之间高程265.0 m处。

根据本文颗粒流方法的模拟结果，蓄水期坝体最大沉降2.24m，发生在坝轴线偏下游高程305 m高程处；上游最大水平位移0.27m，发生在高程287m处，下游最大水平位移0.45 m，发生在高程305 m处。

通过对比可以发现，运用颗粒流方法模拟水布垭面板堆石坝分层填筑过程，模型的宏观变形特征与有限元结果比较接近，这说明利用颗粒流方法模拟超高堆石坝的分层分区填筑过程是切实可行的。通过与现场观测对比可以看出，颗粒流模型的变形小于现场观测值，这主要是由于本文尚未考虑流变的影响，对坝料碾压考虑得也不充分，可以预见，若在颗粒流模型中考虑堆石料的流变，并对坝体碾压进行更加细致的模拟，模拟结果将会更加真实地反映坝体的应力变形特征。

4　总结

本文针对颗粒流方法模拟超高堆石坝分层分区填筑过程的可行性进行了研究，结果表明，颗粒流方法模拟超高堆石坝的填筑过程是切实可行的，从与有限元结果对比可以看出，颗粒流方法的模拟结果是可靠的。在模拟过程中，采用并行算法使得单机所能容纳的颗粒数量明显增加，计算效率极大提高；同时，本文建立了一套快速有效的建模方法，可在复杂边界区域快速生成密实的满足级配要求的颗粒流模型。这两个方面的改进与突破，使得颗粒流方法应用于模拟超高堆石坝分层分区填筑成为现实。

综上所述，本文的研究成果对于颗粒流方法应用于超高堆石坝分层填筑模拟，具有重要的工程应用前景和理论价值。当然，本文的研究中尚未考虑堆石料的流变，对坝料的碾压也考虑的不是很充分，对于这些的不足之处，将在后续的工作中作进一步深入研究，从而使得该模拟方法更加完善。

[1]徐泽平，邓刚.高面板堆石坝的技术进展及超高面板堆石坝关键技术问题探讨[J].水利学报，2008，39（10）:1226-1234.

[2]MaG，ZhouW，ChangXL.Modelingtheparticle breakage of rockfill materials with the cohesive crack model [J].Computers&Geotechnics，2014，61（3）:132-143.

[3]周伟，常晓林，周创兵，等.堆石体应力变形细观模拟的随机散粒体不连续变形模型及其应用 [J].岩石力学与工程学报，2009，28（03）:491-499.

[4]Deluzarche R，Cambou B.Discrete numerical modelling of rockfill dams[J].International journal for numerical and analytical methods in geomechanics，2006，30（11）:1075-1096.

[5]Alaei E，Mahboubi A.A discrete model for simulating shear strength and deformation behaviour of rockfill material, onsidering the particle breakage phenomenon[J].Granular Matter，2012，14（6）:707-717.

[6]李晓柱，刘洋，吴顺川.堆石坝现场碾压试验与离散元数值分析[J].岩石力学与工程学报，2013，（S2）:3123-3133.

[7]刘洋，李晓柱，吴顺川.多块体形状堆石体碾压颗粒破碎数值模拟[J].岩土力学，2014（11）:3269-3280.

[8]Tran T H，Vénier R,Cambou B.Discrete modelling of rock-ageing in rockfill dams[J].Computers&Geotechnics，2009，36（1）:264-275.

[9]Silvani C，Désoyer T，Bonelli S.Discrete modelling of time-dependent rockfill behaviour[J].International Journal for Numerical&Analytical Methods in Geomechanics，2009，33（5）:665-685.

[10]邵磊，迟世春.堆石料单轴流变试验的颗粒流模拟[J].岩土力学，2013，（5）:1487-1494.

[11]Cundall P A，Strack O D L.A discrete numerical model for granular assemblies[J].Geotechnique，1979，29（1）:47-65.

[12]柏树田，崔亦昊.堆石的力学性质[J].水力发电学报，1997（3）: 21-30.

[13]孙其诚，王光谦.颗粒物质力学导论[M].北京:科学出版社，2009.

[14]Thomas P A,Bray J D.Capturing nonspherical shape ofgranularmediawithdiskclusters[J].Journalof GeotechnicalandGeoenvironmentalEngineering，1999，125（3）:169-178.

[15]Jiang M J,Yu H S,Harris D.A novel discrete model forgranularmaterialincorporatingrollingresistance[J]. Computers and Geotechnics，2005，32（5）:340-357.

[16]Ng T T,Dobry R.A non-linear numerical model for soil mechanics[J].International Journal for Numerical and Analytical Methods in Geomechanics，1992，16（4）:247-263.

[17]Itasca Consulting Group,Inc.（2014a）.PFC（particle flow code in 2 and 3 dimensions），version 5.0[User’s manual].Minneapolis，MN:ICG.

[18]杨启贵，刘宁，孙役，等.水布垭面板堆石坝筑坝技术[M].北京:中国水利水电出版社，2010.

[19]汪明元，程展林，林绍忠，等.水布垭面板堆石坝的三维弹塑性数值分析研究[J].岩土力学，2004，（S2）:507-512.

黄小波（1981-），男，大学本科，工程师，从事水利工程设计工作，手机：15907492008。

（2016-02-24）