一种采用相空间重构的多源数据融合方法
2016-12-23赵皓高智勇高建民王荣喜
赵皓,高智勇,高建民,王荣喜
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
一种采用相空间重构的多源数据融合方法
赵皓,高智勇,高建民,王荣喜
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
针对化工生产系统中状态监控变量数量庞大、冗余度高等问题,提出了一种采用相空间重构的多源数据融合方法。该方法首先根据互信息法和Cao方法分别求取相空间重构参数延迟时间和嵌入维数;然后,基于信息熵对自适应加权融合估计方法的融合目标函数进行改进,并利用社会认知优化算法确定各信息源的权重系数,实现多源数据融合;最后,通过实际化工生产系统的数据分析对所提方法进行有效性验证。实验结果表明,相比于传统方法,由该方法得到的重构相空间的信息更加完备,其信息量和平均峰值信噪比分别平均提高135.6%和40.6%。该方法为解决多源异类传感器数据融合问题提供了一种新思路。
相空间重构;数据融合;自适应加权融合估计;信息熵
化工生产系统是典型的耗散系统,其中包含数百甚至更多的监测变量对其状态进行监测,产生了海量的监测时间序列,但同时也带来了大量的冗余信息。多传感器数据融合技术能够将来自多个传感器的信息和数据进行综合分析与处理,在实现多源信息互补的同时能有效降低冗余程度。
数据级融合作为最基础的融合层次,能够提供特征级、决策级所不能提供的详细信息。张品等人采用基于卡尔曼滤波器的贝叶斯估计方法提高了融合精度[1];宾光富等人通过关联函数分析调整加权融合模型权重系数得到了最佳融合结果[2]。然而,目前的数据级融合方法主要是针对同类传感器,针对异类传感器的研究很少,并且最大的问题在于异类传感器获得的是物理意义不同的目标或现象的信息,因此融合结果得不到合理的解释。相空间重构理论则为解决这一问题提供了可能。
相空间重构作为非线性时间序列分析的重要手段,能够将动力系统的吸引子在高维空间中恢复出来。通过相空间重构所得到的是能够反映时间序列动力学特性的信息空间,而原始时间序列所蕴含的物理意义被淡化,因此,可以将多源数据融合问题转化为多变量相空间重构问题。许多学者针对多变量相空间重构问题开展了研究[3-5],但目前的研究方法或只是将各个变量在相空间上进行拓展,增大计算量,或假设数据符合已知的概率分布,并没有很好地解决重构相空间中信息不完备、冗余度高等问题。
针对以上问题,本文将相空间重构理论与数据融合技术相结合,提出了一种解决多源异类传感器数据融合问题的方法。首先,各个单一时间序列都包含并且反映了原复杂系统的部分信息,选择能够反映系统特性的参数分别进行相空间重构;结合数据融合技术,采用改进的自适应加权融合估计的方法对相空间中的每一维数据进行融合,得到包含尽可能多的原复杂系统信息的融合相空间。将本文所提出的方法结合某化工企业分布式控制系统(distributed control system, DCS)数据进行分析,通过对比融合结果可以发现,由本文方法得到的融合相空间能够包含参与融合的各信息源的重要信息,较传统方法得到的融合相空间信息更为完备。
1 多时间序列相空间重构
1.1 相空间重构数学模型
非线性时间序列相空间重构理论的基础是Takens等于1981年提出的嵌入定理,即对于无限长、无噪声的d维混沌吸引子的标量时间序列{x(n)},总可以在拓扑不变的意义上找到一个m维的嵌入相空间,只要维数m≥2d+1[6]。假设一个时间序列为{x(1),x(2),…,x(n-1),x(n)},根据嵌入定理,重构相空间可以表示为X=[x(i),x(i+τ),…,x(i+(m-1)τ)]T∈Rm,i=1,2,…,N,N为相点数且满足N=n-(m-1)τ,τ是延迟时间,m是嵌入维数。本文中分别采用互信息法和Cao方法[7]计算延迟时间和嵌入维数。
1.1.1 互信息法 对于由2个离散信息系统S={s1,s2,…,sK}和Q={q1,q2,…,qF}构成的共同系统,在给定S的情况下可以得到关于系统Q的信息,称为S和Q的互信息
(1)
式中:Psq(si,qj)为事件si、qj的联合分布概率。定义[s,q]=[x(t),x(t+τ)],则互信息是与延迟时间相关的函数,记为I(τ)。取I(τ)的第一个极小值作为最优延迟时间。
1.1.2 Cao方法 对于d维相空间中的第i个相点矢量X(i),都有某个应合并的最邻近点Xmin(i),其距离为Rd(i)。当相空间维数从d维增加到d+1维时,这2个相点间的距离变成Rd+1(i)。令
(2)
定义
(3)
(4)
对于一个确定时间序列,E1(m)将在m大于m0后不再变化,此时m0为选取的嵌入维数。
将上述单时间序列相空间重构方法拓展到多时间序列相空间重构。选取r个变量,分别求取延迟时间τ1,τ2,…,τr和嵌入维数m1,m2,…,mr。为了保证各个变量相空间都能够完全展开,同时在相轨迹不产生压缩的前提下保证数据间的相关性,选取最大的嵌入维数m和最小的延迟时间τ作为相空间重构参数
(5)
由此可以得到r个重构相空间。
1.2 基于自适应加权融合估计的数据融合
随着变量个数的增加,重构相空间在携带更多原系统动力学信息的同时,也很有可能携带冗余信息。信息熵[8]作为一种信息度量的方法,可以定量地衡量信息量的大小,且信息熵与信息量的大小成反比关系[9]。本文据此提出信息度这一概念,并与自适应加权融合估计算法相结合,对融合目标函数进行改进。具体过程为:对于监测时间序列T1,…,Tr,设W1,…,Wr为各时间序列所对应的加权因子,则加权融合后的最终结果为
(6)
数据融合的关键步骤就是要找到目标函数F在式(7)约束条件下的最小值
(7)
传统自适应加权融合估计算法的目标函数为
(8)

(9)

本文提出信息度Y,其表达式为
(10)
由式(10)可知,信息度与信息熵成反比关系,即与信息量成正比关系。上述问题的求解是一个典型的多属性目标优化问题。下面将使用社会认知优化算法对各变量加权因子进行最优解求取。
1.3 基于社会认知优化算法的权重优化
社会认知优化算法(social cognitive optimization,SCO)是由谢晓峰教授提出的一种智能算法[10],在求解复杂非线性问题和多属性优化问题中具有很好的效果[11-12]。该算法主要包括知识点、库、学习代理、邻域搜索等概念,整个优化过程由一系列学习代理来完成。
假设库中知识点个数为Npop,学习代理的个数为Nc(一般情况下Npop=3Nc),循环学习的次数为T。社会认知算法的实现步骤如下[11]。
步骤1 初始化过程:①在知识库(式(7))中随机生成每个知识点对应的加权因子W1,W2,…,Wr和适应度水平(目标函数式(8)或式(9)的值);②随机将知识库中的知识点分配给每个学习代理,但是不允许把一个知识点重复分配给多个学习代理。
步骤2 替代学习过程(针对每个学习代理):①模仿学习过程,从知识库中随机地选出2个或多个知识点(一般选择2个),但是这些选出的知识点不能与学习代理本身的知识点重复,然后基于竞争选择的原则在这几个知识点当中选择出一个较好的知识点(即选取式(8)或(9)的较小者);②观察学习过程,通过比较选择出来的知识点和学习代理自身的知识点的水平,选择水平相对较好的知识点作为中心点x2,使用较差的知识点作为参考点x1,然后学习代理基于邻域搜索的原则(以x1作为参考点选出一个新的点x′,对r维的点x′=x1,r+2rand()(x2,r-x1,r),rand()是属于(0,1)的随机值),根据这2个知识点移动到一个新的知识点,之后将该知识点添加到知识库中。
步骤3 知识库更新过程:从知识库中移除Nc个具有最差水平的知识点。
步骤4 重复步骤2和步骤3,直到满足终止条件。
社会认知优化算法的流程如图1所示。

图1 社会认知优化算法流程图
2 多源数据融合过程
多源数据融合过程分为以下几个步骤。
(1)数据预处理。对原始时间序列进行归一化等处理,同时取出r个需要参加相空间重构的变量。
在煤炭建设大直径煤仓的施工中,往往需要搭设上人梯,而钢管式上人梯最为常见,但施工中须注意搭设方式、附着方式、基础承载力要求,重点考虑受水平荷载(主要是风荷载)影响,因上人梯一般搭设在两个相邻仓之间,该处风荷载通过时会大大加强,因此本文通过实例作了一些总结。
(2)相空间重构参数计算。对选取的r个变量分别求取延迟时间τ1,τ2,…,τr和嵌入维数m1,m2,…,mr,并根据式(5)确定新相空间的嵌入维数m和延迟时间τ。
(3)各变量相空间重构。根据上一步中确定的相空间重构参数,将r个变量分别重构到新的相空间中,其中第i个变量{xi(1),xi(2),…,xi(n)}的重构相空间可以表示为
Yi=[xi(j),xi(j+τ),…,xi(j+(m-1)τ)]T∈Rm
(11)
式中:i=1,2,…r;j=1,2,…,N;N=n-(m-1)τ。
(4)多源数据融合。使用自适应加权融合估计算法对上述r个重构相空间的每一维分别进行数据融合,得到重构相空间
(12)
式中:j=1,2,…,N;N=n-(m-1)τ。其中融合相空间中的第k个坐标点
(13)
式中:xi(k)表示第i个变量的第k个点值;wi(k)为xi(k)的权重。
3 应用实例
将本文所提出的方法应用到某能源化工企业的实际压缩机组所产生的时间序列中,通过对比融合效果,验证本文所提方法的有效性。选取监测点A_ATI7611(监测点1)测量增压机进气温度,选取监测点PSE7655(监测点2)测量空气机组汽轮转速。本文中所采用的数据均直接来源于企业DCS数据,以1 min为间隔,连续采集48 h,共2 882个数据点。
将2个监测点的时间序列重构相空间中前二维分别记为xi,yi,i=1,2,监测点1、2的重构图分别如图2和图3所示。
根据式(5),上述2个监测点融合相空间重构参数选择为嵌入维数m=4,延迟时间τ=4。根据上述参数重新得到重构相空间Y1和Y2,将2个相空间中的每一维数据按照500的数据量进行分块,使用社会认知优化算法 (设定参数Npop= 300,Nc=100,T=1 000),分别计算在目标函数为式(8)和(9)的条件下每一维中每一个数据块的权重,结果分别如表2和表3所示(目标函数为式(9)时求得的每一维的权重系数相同,因此只列举第1维)。

表1 监测点1和2的相空间重构参数

图2 监测点1时间序列重构图

图3 监测点2时间序列重构图
分别根据上述权重值以及Y1、Y2的相点值,重新计算融合相空间Z中的每一个相点。Z中的前二维分别记为z1、z2,融合后的相空间轨迹图分别如图4、5所示。

表2 目标函数为式(8)时数据块权重计算结果

表3 m=1目标函数为式(9)时数据块权重计算结果

图4 传统方法得到的融合相空间轨迹图

图5 本文方法得到的融合相空间轨迹图
4 融合效果评价
4.1 定性评价
对比图2、3可以发现,图2不包含图3的球形特征,图3也不具备图2的椭圆形特征,即两者的重构信息都是不完备的。对比图4、5可以发现,图4中包含图3的球形特征,但并不包含图2的椭圆形特征,而图5在整体上与图2相似,含有椭圆形特征,同时在左下角含有图3的球形特征。因此,本文所提出的改进方法较传统方法具有更好的融合效果。
4.2 定量评价
(1)信息量。由式(10)知,本文中所提出的信息度的大小与时间序列中所包含的信息量成正比关系。分别求取图2~图5相空间每一维度的信息度值,结果如表4所示。

表4 各维度相空间信息度
从表4中可以看出,本文所提出的方法使得融合后相空间中每一维度的信息度值都为最大,即所包含的信息量最大,相比于传统方法平均提高了135.6%,因此具有更好的融合效果。
(2)平均峰值信噪比。在图像融合中常用峰值信噪比来衡量融合后的噪声是否得到抑制[13]。在这里认为原始相空间与融合相空间的差异就是噪声,而原始相空间就是信息。定义原始相空间Y与融合相空间Z的均方根误差为
(14)
式中:m、N分别表示相空间的维数与相点个数;Y(i,j)、Z(i,j)分别为原始相空间与融合相空间的相点值。则峰值信噪比的计算公式为
(15)
峰值信噪比越大,则说明融合的效果越好。本文据此定义平均峰值信噪比
(16)
式中:RPSN(i)表示参与融合的第i个变量的峰值信噪比;r表示参与融合的变量个数。对比2种方法的计算结果,如表5所示。
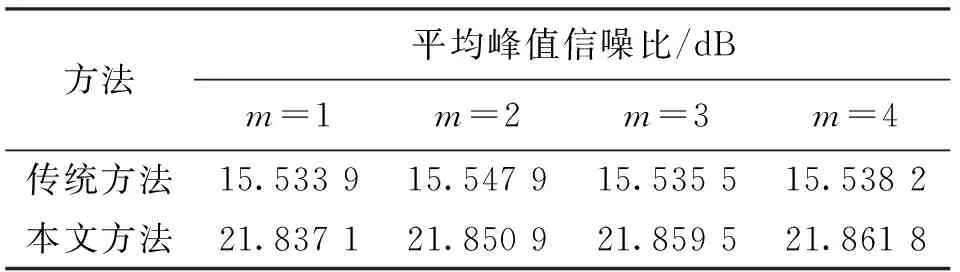
表5 2种方法各维度平均峰值信噪比比较
从表5中可以看出,本文中所提出的改进方法具有更大的平均峰值信噪比,相比于传统方法提高了40.6%。
综合上述对比结果可以看出:相比于传统方法,由本文所提出的多源数据融合方法得到的融合相空间信息更加完备,具有更好的融合效果。
5 结 论
本文针对复杂系统中状态监控变量数量庞大、冗余度高等问题,提出了一种采用相空间重构的多源数据融合方法。通过具体的实例验证分析表明,由本文方法得到的融合相空间包含了所有参与融合的各信息源的重要信息,其信息空间更加完备,为后续的数据分析奠定了良好的数据基础。该方法不仅可以解决同类传感器之间的数据融合问题,也为异类传感器的数据融合问题提供了一种新思路。
[1] 张品, 董为浩, 高大冬. 一种优化的贝叶斯估计多传感器数据融合方法 [J]. 传感技术学报, 2014(5): 643-648. ZHANG Pin, DONG Weihao, GAO Dadong. An optimal method of data fusion for multi-sensors based on Bayesian estimation [J]. Chinese Journal of Sensors and Actuators, 2014, 27(5): 643-648.
[2] BIN Guangfu, JIANG Zhinong, LI Xuejun, et al. Weighted multi-sensor data level fusion method of vibration signal based on correlation function [J]. Chinese Journal of Mechanical Engineering, 2011, 24(5): 899-904.
[3] GARCIA S P, ALMEIDA J S. Multivariate phase space reconstruction by nearest neighbor embedding with different time delays [J]. Physical Review: E, 2005, 72(2): 027205.
[4] WANG Rongxi, GAO Jianmin, GAO Zhiyong, et al. Data fusion based phase space reconstruction from multi-time series [J]. International Journal of Database Theory and Application, 2015, 8(6): 101-110.
[5] 从蕊, 刘树林, 马锐. 基于数据融合的多变量相空间重构方法 [J]. 物理学报, 2008, 57(12): 7487-7493. CONG Rui, LIU Shulin, MA Rui. An approach to phase space reconstruction from multivariate data based on data fusion [J]. Acta Physica Sinica, 2008, 57(12): 7487-7493.
[6] TAKENS F. Detecting strange attractors in turbulence [J]. Lecture Notes in Mathematics, 1981, 898: 366-381.
[7] PALIT S K, MKHERJEE S, BHATTACHARYA D K. A high dimensional delay selection for the reconstruction of proper phase space with cross auto-correlation [J]. Neurocomputing, 2013, 113: 49-57.
[8] SHANNON C E. A mathematical theory of communication [J]. The Bell System Technical Journal, 1948, 27(3): 379-423.
[9] 张继国, 辛格. 信息熵: 理论与应用 [M]. 北京: 中国水利水电出版社, 2012: 35-46.
[10]XIE Xiaofeng, ZHANG Wenjun, YANG Zhilian. Social cognitive optimization for nonlinear programming problem [C]∥Proceedings of International Conference on Machine Learning and Cybernetics. Piscataway, NJ, USA: IEEE, 2002: 779-783.
[11]MA Li, WANG Rongxi, CHEN Yanpin. The Social cognitive optimization algorithm: modifiability and application [C]∥Proceedings of International Conference on E-Produce E-Service and E-Entertainment. Piscataway, NJ, USA: IEEE, 2010: 1-4.
[12]ZHANG Jianke, LIU Sanyang, WANG Rongxi. Control of chaotic systems by chaotic social cognitive optimization [J]. ICIC Express Letters, 2011, 5(3): 693-699.
[13]刘贵喜, 杨万海. 基于小波分解的图像融合方法及性能评价 [J]. 自动化学报, 2002, 28(6): 927-934. LIU Guixi, YANG Wanhai. A wavelet decomposition based image fusion scheme and its performance evaluation [J]. Acta Automatica Sinica, 2002, 28(6): 927-934.
[本刊相关文献链接]
董恩清,刘伟,宋洋.采用三角形节点块处理无线传感器网络节点定位中节点翻转歧义的迭代方法.2015,49(4):84-90.[doi:10.7652/xjtuxb201504014]
徐田华,杨连报,胡红利,等.高速铁路信号系统异构数据融合和智能维护决策.2015,49(1):72-78.[doi:10.7652/xjtuxb 201501012]
司刚全,张寅松,赵为犁.考虑可信度评价的多传感器一致性鲁棒测度方法.2013,47(8):7-11.[doi:10.7652/xjtuxb2013 08002]
司刚全,张寅松,娄勇.考虑自支持度和互支持度的多传感器一致性测度算子.2012,46(10):20-23.[doi:10.7652/xjtuxb 201210004]
宋渤,徐龙起,张桂铭,等.采用微传感器的黏/密度实验系统及其性能测试.2014,48(3):44-48.[doi:10.7652/xjtuxb 201403009]
(编辑 刘杨)
A Fusion Method of Multisource Data Using Phase Space Reconstruction
ZHAO Hao,GAO Zhiyong,GAO Jianmin,WANG Rongxi
(State Key Laboratory for Manufacturing System Engineering, Xi’an 710049, China)
A new fusion technology for multi-source data based on the phase space reconstruction is proposed to focus on the problem of multivariable and high redundancy of the condition monitoring variables in the chemical production system. Both the mutual information method and the Cao method are used to select the reconstruction parameters, the time delay and the embedding dimension. Then, the information entropy is employed to obtain an improved objective function in adaptive weighted fusion estimating method for multisource data fusion, and the weighting coefficients of various information sources are calculated by means of a social cognitive optimization algorithm. The effectiveness of the proposed method is verified by an analysis of one case study of real chemical plant data sets. The results and a comparison with the traditional method show that the proposed method gets improvements in the amount of information and average PSNR, respectively. It is concluded that the proposed method improves the completeness of the information of the reconstructed phase space and provides a new approach for the multi-source data fusion of heterogeneous sensors.
phase space reconstruction; data fusion; adaptive weighted fusion estimation; information entropy
10.7652/xjtuxb201608014
2016-01-12。 作者简介:赵皓(1993—),男,硕士生;高智勇(通信作者),男,副教授,博士生导师。 基金项目:国家自然科学基金资助项目(51375375)。
时间:2016-06-28
http:∥www.cnki.net/kcms/detail/61.1069.T.20160628.2029.006.html
TP212
A
0253-987X(2016)08-0084-06
