一种适用于中高轨合成孔径雷达卫星的分辨率分析方法

张欣,黄普明,文珺,王伟伟

(1.中国空间技术研究院西安分院,710000,西安;2.广西大学计算机与电子信息学院,530004,南宁)



一种适用于中高轨合成孔径雷达卫星的分辨率分析方法

张欣1,黄普明1,文珺2,王伟伟1

(1.中国空间技术研究院西安分院,710000,西安;2.广西大学计算机与电子信息学院,530004,南宁)

针对中高轨合成孔径雷达(SAR)卫星运动轨迹复杂、导致传统SAR卫星分辨率分析方法不再适用的问题,提出了一种分析中高轨SAR卫星理论分辨率的时域模糊函数(TDAF)方法。该方法根据分辨率的定义,从时域模糊函数进行推导,利用归一化模糊函数求解任意方向上的空间分辨率,然后以地面分辨椭圆的方式对中高轨SAR卫星分辨率进行描述,更加完备地表征了曲线运动轨迹的中高轨SAR系统分辨特性。结合后向投影算法仿真验证了基于TDAF算法的有效性。仿真结果表明,TDAF方法可以精确计算中高轨SAR卫星的理论分辨率,误差在±1%以内,可为中高轨SAR卫星的轨道设计及成像性能指标分析提供依据。

合成孔径雷达;分辨率;模糊函数;后向投影算法

将星载合成孔径雷达(synthetic aperture radar,SAR)的轨道升高至中高轨道[1-2],能大大提高监测的时间分辨率和可视范围,且结合波束控制技术,可以对突发事件进行快速响应,但轨道的升高带来了许多不同于低轨SAR的问题,例如弯曲轨迹成像处理[3-4]、二维姿态控制[5]、电离层影响[6-7]以及二维空间分辨率分析[8-10]等。对于低轨SAR,成像关系简单,在合成孔径时间内可以认为平台是匀速直线运动,很容易得到分辨率的解析表达式。但是,对于中高轨SAR,由于合成孔径时间长,受地球自转影响严重,相对运动轨迹复杂,因而传统低轨和机载SAR的分辨率计算公式不再适用[10],地面分辨率计算无法得到精确解析表达式,且传统距离向和方位向分辨率的物理意义也变得模糊,在中高轨SAR系统设计和论证时,不仅需要知道二维旁瓣的分辨率,也需要知道最优和最差的分辨率[11]。

目前分析分辨率的方法主要有两种,一种是基于广义模糊函数的方法[11-12],另一种是基于相位梯度的方法[13-15],这些算法主要应用于双基SAR。针对中高轨SAR,文献[8]引入广义模糊函数(generalized ambiguity function,GAF),提出利用求解相邻目标点回波信号的相关函数计算空间二维空间分辨率的方法。该方法首先采用帕萨瓦尔定理将时域积分变换到频域进行求解,然后利用一阶泰勒展开推导模糊函数的近似表达式,由于在计算地距分辨率的时候没有考虑波束入射角影响,且认为地球自转角速度和SAR卫星运行角速度大小相同,因此当轨道有偏心率和轨道倾角时会给分辨率的计算带来误差。文献[9]基于相位梯度法对中高轨SAR的地面分辨率进行了理论分析,由于没有考虑卫星速度的时变特性,因而只有在较短的合成孔径时间内,该方法才是有效的。文献[10]考虑了入射角的影响,分析了地距分辨率,同时在相位梯度法基础上利用介值定理,求解方位分辨率的取值范围。该方法计算的不是旁瓣扩展方向上的分辨率,也不对应于最优和最差分辨率方向,无法完备地表征中高轨SAR系统分辨率特性。

为了解决上述问题,本文提出了一种分析中高轨SAR卫星理论分辨率的时域模糊函数(time-domain ambiguity function,TDAF)方法,同时以地面分辨椭圆的方式对中高轨SAR系统分辨特性进行描述,并结合时域后向投影(back projection,BP)算法仿真验证了本文算法的有效性。

1 广义模糊函数分析

相比于低轨道卫星,中高轨SAR卫星受地球自转影响严重,星地几何关系复杂,传统的基于直线运动轨迹的星地几何关系不再适用。本文将中高轨SAR星地几何关系建立在如图1所示的地球固定坐标系O-XYZ下,图中虚线表示中高轨SAR卫星的曲线运动轨迹。设雷达发射的是线性调频信号,则目标点P的基带回波信号为

(1)

式中:σ为后向散射系数,这里假设不考虑后项散射系数的影响,即设σ为1;wr(·)、wa(·)分别为线性调频信号的窗函数和方位窗函数;γ为信号调频率;tk、tm分别为快时间和慢时间;c为光速;fc为载波频率;R(tm,P)为雷达到目标点P的双程斜距历程。

图1 中高轨SAR星地几何关系示意图

下面利用广义模糊函数的定义对中高轨SAR理论分辨率进行分析。首先,定义测绘带内一个参考目标点PA和一个相邻的目标点PB,如图1所示,其回波信号分别为s(tk,tm,PA)和s(tk,tm,PB)。模糊函数定义为相邻目标点回波信号与参考点回波信号的互相关函数[8]

(2)

式中

(3)

(4)

Tp为发射信号脉冲宽度。对式(4)进一步变换可得

(5)

(6)

(7)

因此,式(2)可以变换为

(8)

式中:B=γ(Tp-2|τ2(tm)|);Ts为合成孔径时间。观察式(8),由于目标点PA和PB相邻,因此对斜距差R(tm,PA)-R(tm,PB)在合成孔径中心时刻进行一阶泰勒展开，近似有

(9)

式中:R0,Δ、v0,Δ分别为合成孔径中心时刻卫星到目标点PA与PB的距离差和径向速度差。将式(9)带入到式(8)可以得到

(10)

进一步,由于目标点PA和PB相邻,有B≈Br=γTp,Br为雷达发射信号带宽,sinc[B(R0,Δ+v0,Δtm)/c]≈sinc(BrR0,Δ/c);同时,假设方位向天线归一化功率方向图在合成孔径时间内近似为矩形窗,式(10)可以变换为

(11)

2 分辨特性分析

通过近似后的式(11)只能求出斜距平面二维旁瓣的分辨率,对于其他方向的分辨率还是无法得到解析解,同时对于地距平面的分辨率也无法直接获得。观察式(8),将式(8)写成时域离散形式

(12)

式中:N为合成孔径时间内积累脉冲数;tm,n为发射第n个脉冲的时间。为了得到中高轨SAR空间分辨率,需要对广义模糊函数进行归一化,有

(13)

由分辨率的定义可知,当χn(PA,PB)=21/2/2时,即可得到沿PA-PB方向上的分辨率

(14)

可根据式(13)和式(14)通过计算机仿真准确计算任意方向的分辨率,且只需要知道卫星的轨迹即可,没有其他假设条件,中高轨SAR卫星运动轨迹可以根据卫星的轨道参数计算得到。

为了更加完备地表征中高轨SAR系统的分辨率特性,以地面分辨椭圆的方式对中高轨SAR分辨率进行描述,这样可以直观给出地面目标点在各个方向上的分辨率。首先,假设待分析的目标点PA的坐标为(纬度,经度),为了方便分辨椭圆的分析,以极坐标的形式给出各个方向上的分辨率,设

(15)

式中:θ为极坐标角度(与零经度方向的夹角),取值范围[0°,360°];ΔL为经纬度间隔,ΔL的取值越小分辨率计算精度越高,本文仿真中取1×10-5(°);l为目标点PB在θ方向上距离目标点PA的经纬度间隔。根据公式(13)和(14)通过计算机仿真的方法即可得到目标点PA在θ方向上的分辨率,事实上,由于分辨椭圆的对称性,只需要求出θ在[0°,180°]范围内的分辨率就能画出分辨率椭圆。

3 不同成像模式下分辨率的分析

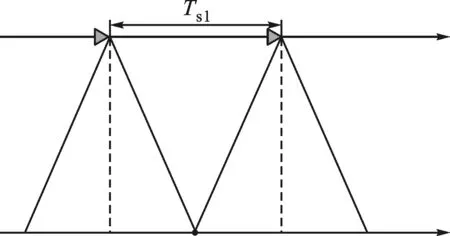
(a)条带模式

(b)聚束模式

(c)ScanSAR模式图2 不同成像模式示意图

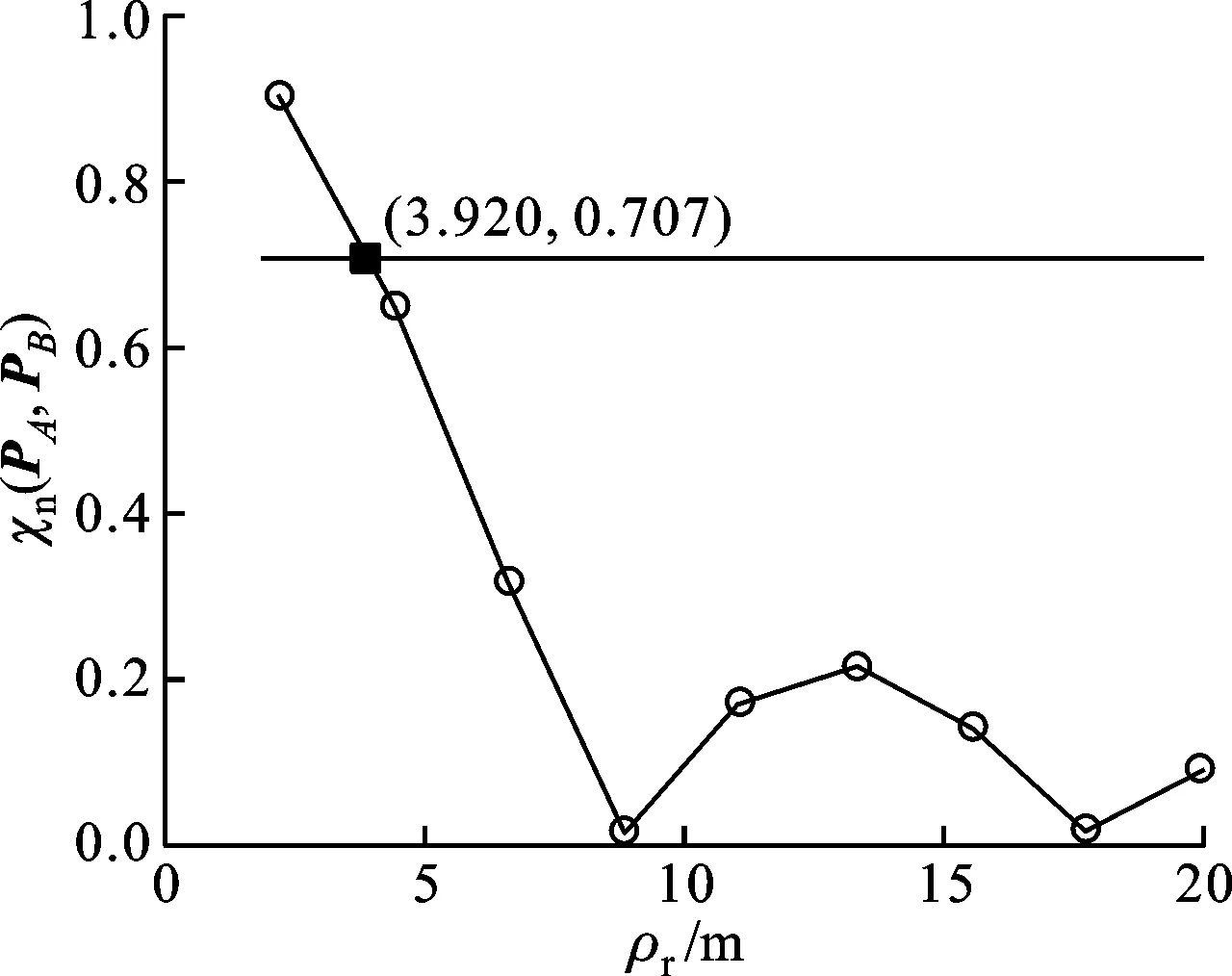
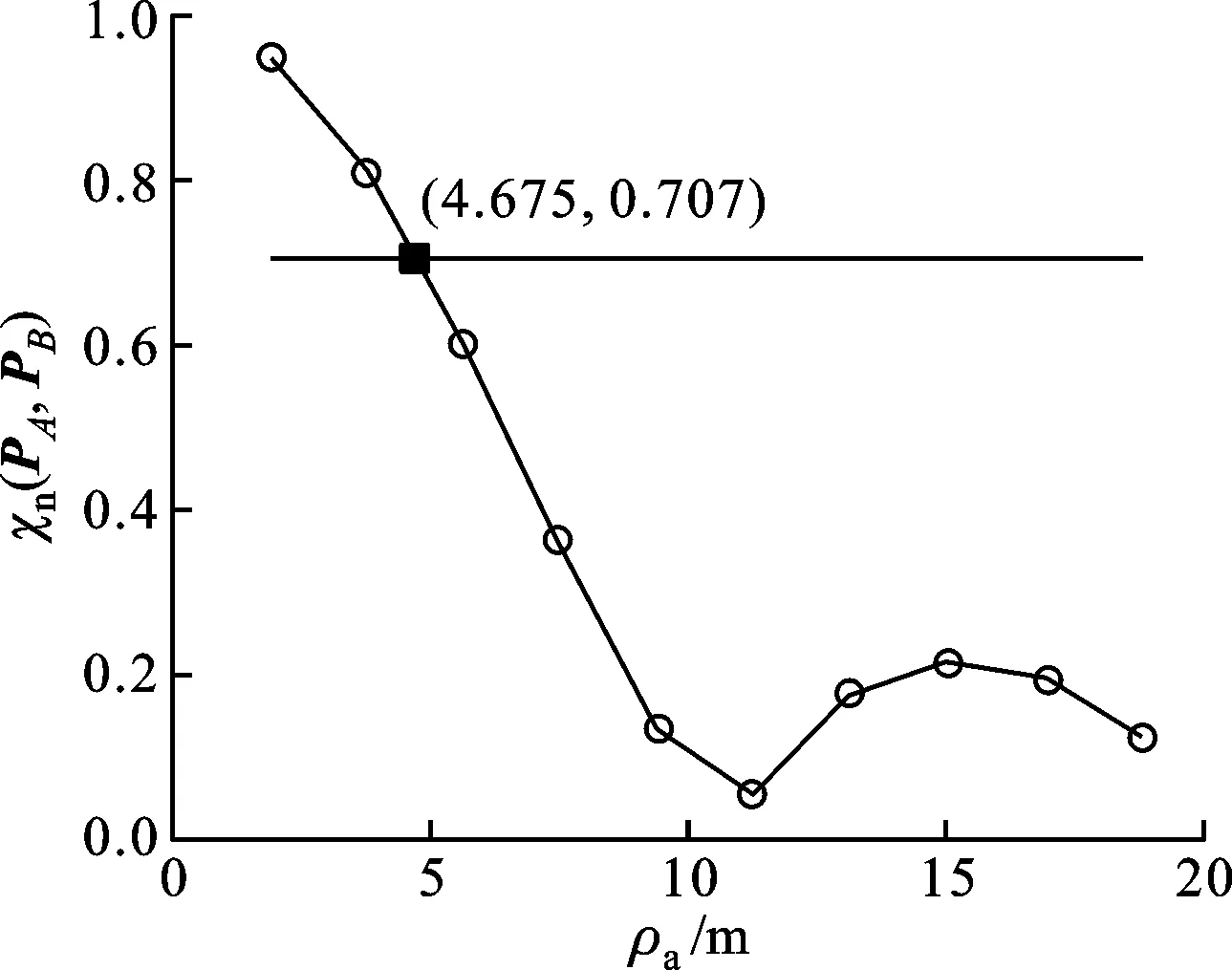
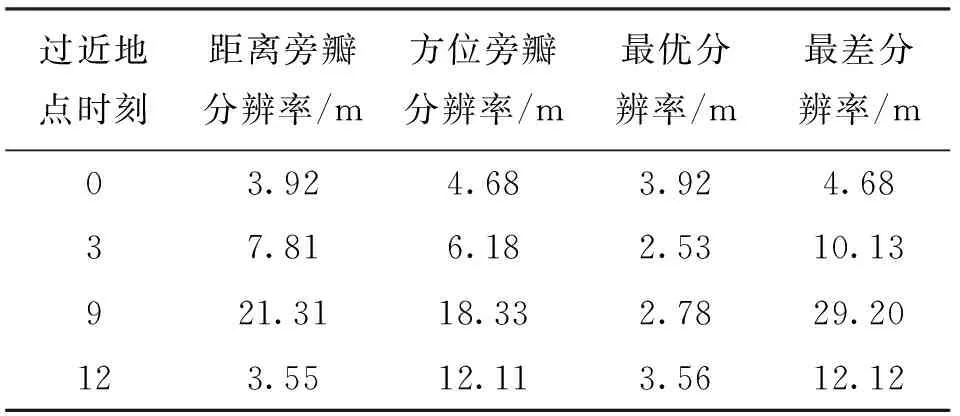
目前常用的成像模式有条带、聚束和ScanSAR模式。条带模式如图2a所示,所有目标被波束完整扫过,合成孔径时间Ts1主要由天线的方位向波束宽度决定。聚束模式如图2b所示,是通过调整方位向天线波束指向来增加对某一特定区域的合成孔径时间Ts2,以提高方位向分辨率。ScanSAR模式则是通过俯仰向波束的扫描,使得每一个目标被部分波束照射,每个俯仰角度对应一个字条带。图2c给出了一个子条带的ScanSAR模式示意图,图中Ts3为雷达波束开始照射该子条带到离开的时间,点画线代表的波束为下一次照射该子条带的位置。可以看出,ScanSAR模式是通过减小合成孔径时间,以降低分辨率为代价来提高测绘带宽。通过以上分析,可得出Ts3

本文所提出的TDAF方法是从广义模糊函数和成像分辨率的基本定义出发,推导了适用于中高轨SAR卫星理论分辨率的计算公式。从式(13)可以看出,本文方法只需已知雷达到目标点的斜距历程,因此针对不同的成像模式,首先要确定不同成像模式下的合成孔径时间Ts,然后计算出该时间段内卫星的运动轨迹和目标点的位置,得到雷达到目标点的斜距历程,进而利用式(13)即可分析该成像模式下的理论分辨率。

4 仿真实验分析

下面对本文所提的分辨率分析方法进行仿真验证。由于传统的距离多普勒(rangeDoppler,RD)算法、线频调变标(chirpscaling,CS)算法等频域算法主要适用于直线运动轨迹的SAR成像,而对于曲线运动轨迹的中高轨SAR会损失成像性能,因此不适用于验证本文方法的有效性。后向投影(BP)算法是最精确的成像处理算法,它适合曲线运动轨迹的SAR成像。需要指出的是,成像算法不会影响到理论分辨率。当SAR卫星系统设计完成后,距离向理论分辨率仅和发射信号带宽,波束入射角有关;而方位向理论分辨率仅与星地几何构型及SAR工作模式有关。目前有论文研究了中高轨SAR的频域成像算法[3-4],但这些成像算法都需要知道精确的卫星轨迹并利用泰勒级数拟合斜距历程,在准确知道卫星运动轨迹的前提下,这些频域成像算法和BP算法成像分辨率是一致的。因此,本文采用成像平面为地距平面的BP算法来对目标点进行仿真。中高轨SAR系统仿真参数如表1所示。

为了验证本文TDAF方法的有效性,首先选取卫星过近地点0时刻时的波束中心与地求表面交点(32.21°N,106°E)为仿真目标点,轨道参数如表1所示,这个时刻卫星等效斜视角为0,等效于正侧视,通过式(13)计算得到的沿距离向和方位向距离ρ=2|PA-PB|变化的归一化模糊函数χn(PA,PB)的衰减曲线如图3所示。当χn(PA,PB)=21/2/2时,计算可得距离向分辨率和方位向分辨率分别为3.92m和4.68m。实际分辨率可通过BP算法仿真得到,为3.99m和4.72m,误差分别为-0.07m和-0.04m。

表1 中高轨SAR仿真参数

(a)沿距离向

(b)沿方位向图3 目标点(32.21°N,106°E)的归一化模糊函数衰减曲线

(a)过近地点0时刻 (b)过近地点3时刻 (c)过近地点9时刻 (d)过近地点12时刻图4 目标点成像结果等高线图

由于中高轨SAR几何构型的复杂性,二维旁瓣扩展方向不是正交的,不再是地面分辨椭圆的长轴和短轴方向,即对应中高轨SAR系统的最差和最优分辨率[11],且全轨道的分辨率是变化的。因此,在中高轨SAR系统设计和论证时,不仅需要知道二维旁瓣方向上的分辨率,也需要知道全空间分辨率。将卫星过近地点时刻定义为过近点0时刻，以此为时间起点，选取卫星过近地点的0、3、9、12时刻的轨道位置，分别以这4个轨道位置的波束中心与地球表面交点(32.21°N,106°E)、(26.47°N,115.24°E)、(5.68°N,112.01°E)、(2.30°N,105.93°E)为仿真目标点,仿真地面分辨椭圆曲线,并与通过BP算法得到的实际分辨椭圆进行对比。

图4分别给出了这4个目标点的BP成像结果轮廓图,可以看出,这4个目标点聚焦效果良好,且只有在过近地点0时刻时目标点的二维旁瓣是正交的,其余3个目标点二维旁瓣存在一定的耦合。图5为采用本文算法的地面分辨椭圆曲线,其中0°方向为经度方向,90°方向为纬度方向,极径大小为分辨率,单位为m。

图6给出了采用式(14)和式(15)计算的理论分辨率与BP成像结果的分辨率的误差,在不同轨道位置分辨率计算误差均在±1%以内,验证了本文算法的有效性。而通过文献[10]给出的方法计算的误差最大可达15%,且不能计算其他方向上的分辨率。

进一步从图5可以看出,在过近地点0时刻,距离和方位旁瓣方向分别对应最差,最优分辨率方向,而在其他轨道时刻,距离、方位旁瓣方向与最差和最优分辨率方向不重合,各方向分辨率大小如表2所示,因此以距离旁瓣、方位旁瓣分辨率去做系统设计和论证时会引入一定的误差。通过图5中地面分辨椭圆的描述方式,能够更加完备地表征中高轨SAR系统的分辨率特性。

(a)过近地点0时刻 (b)过近地点3时刻 (c)过近地点9时刻 (d)过近地点12时刻图5 目标点地距分辨椭圆

(a)过近地点0时刻 (b)过近地点3时刻 (c)过近地点9时刻 (d)过近地点12时刻图6 本文所提算法与BP成像图像的分辨率误差率

在Intel(R) Core (TM)2 T6570@2.10 GHz,4 GB RAM,MATLAB (R2012b)的仿真环境下,仿真1个方向上的分辨率需要2 s,本文将[0°,180°]范围50等分,共需要100 s计算这50个方向上的分辨率,进而得到分辨椭圆,而用BP成像算法,得到1个目标点聚焦结果需要3 h。可见,本文所提算法能够快速得到地距分辨椭圆,因此对系统实际设计具有指导价值。

表2 不同时段距离、方位旁瓣及最优、最差分辨率

5 结 论

本文利用广义模糊函数和成像分辨率的定义,推导了归一化时域模糊函数的表达式,提出了一种基于TDAF的中高轨SAR卫星理论分辨率的分析方法;同时,通过地面分辨椭圆的描述方式,更加完备地表征了中高轨SAR系统的分辨率特性。仿真结果表明,通过本文方法计算的地面分辨椭圆和采用BP算法得到的分辨椭圆误差在±1%以内,因此,本文方法可以为中高轨SAR卫星轨道设计及成像性能指标分析提供依据。

[1] RUIZ-RODON J, BROQUETAS A, MAKHOUL E, et al. Nearly zero inclination geosynchronous SAR mission analysis with long integration time for earth observation [J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6379-6391.

[2] HOBBS S, MITCHELL C, FORTE B, et al. System design for geosynchronous synthetic aperture radar missions [J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(12): 7750-7763.

[3] SUN Guangcai, XING Mengdao, WANG Yong, et al. A 2-D space-variant chirp scaling algorithm based on the RCM equalization and subband synthesis to process geosynchronous SAR data [J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(8): 4868-4880.

[4] 李财品, 何明一. 基于Chirp_z变换与方位变标地球同步轨道SAR成像算法 [J]. 电子与信息学报, 2015, 37(7): 1736-1741. LI Caipin, HE Mingyi. Imaging algorithm for geosynchronous orbit SAR based on chirp_z transform and azimuth scaling [J]. Journal of Electronics & Information Technology, 2015, 37(7): 1736-1741.

[5] ZHANG Qingjun, YIN Wei, DING Zegang, et al. An optimal resolution steering method for geosynchronous orbit SAR [J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(10): 1732-1736.

[6] TIAN Ye, HU Cheng, DONG Xichao, et al. Theoretical analysis and verification of time variation of background ionosphere on geosynchronous SAR imaging [J]. IEEE Geoscience and Remote Sensing Letters, 2014, 12(4): 721-725.

[7] 李亮, 洪峻, 明峰, 等. 电离层时空变化对中高轨SAR成像质量的影响分析 [J]. 电子与信息学报, 2015, 36(4): 915-922. LI Liang, HONG Jun, MING Feng, et al. Study on ionospheric effects induced by spatio-temporal variability on medium-earth-orbit SAR imaging quality [J]. Journal of Electronics & Information Technology, 2015, 36(4): 915-922.

[8] HU Cheng, LONG Teng, ZENG Tao, et al. The accurate focusing and resolution analysis method in geosynchronous SAR [J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3548-3563.

[9] WU Zhouting, HUANG Lijia, HU Donghui, et al. Ground resolution analysis based on gradient method in geosynchronous SAR [C]∥IEEE International Conference on Signal Processing, Communication and Computing. Piscataway, NJ, USA: IEEE, 2013: 1-4.

[10]陈溅来, 李震宇, 杨军, 等. 地球同步轨道SAR曲线轨迹二维空间分辨率分析 [J]. 西安电子科技大学学报, 2015, 42(1): 62-68. CHEN Jianlai, LI Zhenyu, YANG Jun, et al. Analysis of the two-dimensional spatial resolution for the curved trajectory of GEO SAR [J]. Journal of Xidian University, 2015, 42(1): 62-68.

[11]龙杰, 姚迪, 孙英钦, 等. 基于分辨椭圆的前斜SAR分辨率分析方法 [J]. 电子学报, 2013, 41(12): 2493-2498. LONG Jie, YAO Di, SUN Yingqin, et al. The method of resolution analysis based on distinguishable ellipse in squinted SAR [J]. Acta Electronica Sinica, 2013, 41(12): 2493-2498.

[12]ZENG Tao, CHERNIAKOV M, LONG Teng. Generalized approach to resolution analysis in BSAR [J]. IEEE Transactions on Aerospace and Electronic System, 2005, 41(2): 461-474.

[13]CARDILLO G P. On the use of the gradient to determine bistatic SAR resolution [C]∥Antennas and Propagation Society International Symposium. Piscataway, NJ, USA: IEEE, 1990: 1032-1035.

[14]仇晓兰, 丁赤飚, 胡东辉. 双站SAR成像处理技术 [M]. 北京: 科学出版社, 2010: 46-58.

[15]TIAN Weiming, ZENG Tao. Resolution characteristic analysis for space-surface BiSAR [C]∥IET International Radar Conference 2009. Steverage, UK: IET, 2009: 1-4.

[本刊相关文献链接]

翟永惠,吴江,王鼎.采用时延估计的外辐射源雷达杂波抑制算法.2015,49(12):47-52.[doi:10.7652/xjtuxb201512008]

吴健平,王国宏,孙殿星,等.集中式雷达网鉴别虚假航迹的假设检验方法.2015,49(2):80-85.[doi:10.7652/xjtuxb 201502014]

杜晓林,苏涛,朱文涛,等.一种多输入多输出雷达相位编码信号的设计方法.2014,48(12):93-99.[doi:10.7652/xjtuxb 201412015]

陈倩倩,张磊,徐刚,等.利用多通道联合稀疏重建的干涉逆合成孔径雷达三维成像算法.2014,48(12):100-106.[doi:10.7652/xjtuxb201412016]

董祺,张磊,徐刚,等.采用子孔径分割的逆合成孔径雷达成像包络对齐方法.2014,48(12):107-112.[doi:10.7652/xjtuxb201412017]

孟自强,李亚超,李浩林,等.双/多基地合成孔径雷达前视三维分辨力研究及运动参数设计.2014,48(8):29-35.[doi:10.7652/xjtuxb201408006]

杨桃丽,索志勇,李真芳,等.地球同步轨道合成孔径雷达干涉测量模型.2014,48(4):85-89+101.[doi:10.7652/xjtuxb 201404015]

侯兴松,张兰,肖琳.合成孔径雷达图像的贝叶斯压缩感知重构算法.2013,47(8):74-79.[doi:10.7652/xjtuxb201308013]

卢锦,苏洪涛,水鹏朗,等.辅助粒子滤波实现天波超视距雷达弱目标似然比检测.2013,47(8):93-97.[doi:10.7652/xjtuxb201308016]

朱磊,水鹏朗,章为川,等.利用区域划分的合成孔径雷达图像相干斑抑制算法.2012,46(10):83-88.[doi:10.7652/xjtuxb201210015]

李世忠,王国宏,白晶,等.压制干扰下雷达网点目标概率多假设跟踪算法.2012,46(10):101-106.[doi:10.7652/xjtuxb 201210018]

杨晓超,刘宏伟,王勇,等.利用多输入多输出雷达低秩杂波的降维空时自适应算法.2012,46(8):76-81.[doi:10.7652/xjtuxb201208014]

朱军涛,廖红建,谢勇勇,等.采用短时傅里叶变换的铁路车载探地雷达数据解译方法.2012,46(7):108-114.[doi:10.7652/xjtuxb201207020]

张立峰,王彤,吴建新,等.机载雷达目标空时参数快速估计方法.2012,46(2):135.[doi:10.7652/xjtuxb201202023]

牛威,苏威,郝培杰,等.利用雷达散射截面积序列的特定航天器工作平台分类识别方法.2011,45(12):53-58.[doi:10.7652/xjtuxb201112010]

(编辑 刘杨)

New Resolution Analysis Method for High Medium-Earth Synthetic Aperture Radar Satellites

ZHANG Xin1,HUANG Puming1,WEN Jun2,WANG Weiwei1

(1. China Academy of Space Technology Xi’an, Xi’an 710000, China; 2. School of Computer, Electronics and Information in Guangxi University, Nanning 530004, China)

A simple and efficient method based on time-domain ambiguity function (TDAF) to analyze theoretical resolution is proposed to solve the problem that the traditional method of resolution analysis is no longer applicable for the high medium-earth-orbit synthetic aperture radar (SAR) satellite with a complicated relative moving trajectory. The definition of imaging resolution is utilized to derive accurate resolution in any direction from the time-domain function and the normalized ambiguity function. Then, the distinguishable ellipse on the ground is used to fully describe the resolution characteristics of the high medium-earth-orbit SAR. Simulations are performed to verify the correctness of the proposed algorithm. The results show that the proposed method achieves high accuracy of the high medium-earth-orbit SAR resolution and the error is within ±1%. It can be concluded that the method could provide guidances for orbit design of high medium-earth-orbit SAR and analysis of imaging performance index.

synthetic aperture radar; resolution; ambiguity function; back projection algorithm

10.7652/xjtuxb201608012

2016-03-08。 作者简介:张欣(1987—),男,博士生;黄普明(通信作者),男,研究员,博士生导师。 基金项目:国家自然科学基金资助项目(61461007)。

时间:2016-06-28

http:∥www.cnki.net/kcms/detail/61.1069.T.20160628.2027.004.html

TN957

A

0253-987X(2016)08-0070-07