结合改进粒子群的非线性盲源分离方法研究

陆建涛,成玮,訾艳阳,

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)



结合改进粒子群的非线性盲源分离方法研究

(西安交通大学机械制造系统工程国家重点实验室,710049,西安)

针对传统非线性盲源分离(NBSS)算法容易陷入局部最优解从而导致分解精度较低的问题,提出一种基于改进粒子群优化(PSO)的NBSS算法。该方法利用多层感知机(MLP)拟合非线性混合的逆过程,并将分离信号的互信息最小作为优化目标(PSO的适应度),从而实现MLP中参数的优化。然而,标准PSO算法存在粒子早熟从而使待优化问题陷入局部最优解,针对这一问题,对适应度低的一部分粒子进行依概率的杂交和变异,使粒子群体在整个迭代过程中保持多样性,从而有效解决标准PSO算法的粒子早熟问题。仿真和试验结果表明,相比于线性盲源分离算法和基于标准PSO的NBSS算法,提出的算法可以从非线性混合机械信息中提取纯净的独立源信息,并且提高了非线性混合源的分离精度,为机械系统的监测诊断和振动噪声溯源提供科学依据和关键技术。

非线性盲源分离;粒子群优化;粒子早熟;交叉变异

随着现代计算机和传感技术的发展,多传感器在状态监测和故障诊断领域的应用越来越广泛[1]。受到系统内部结构、传递路径和噪声等影响,传感器接收到的信号为各独立振源的非线性混合,能否从获得的多维数据中分离出纯净的源信息严重影响着机械故障诊断的准确性和可靠性[2-3]。常用的信号处理方式如傅里叶(FFT)和小波变换等,并未分析混合信号的本质构成,分析结果很大程度上取决于基函数的选择。因此,如何从非线性混合信号中分离出振源信息具有重要的研究意义。

盲源分离(BSS)是在源信号和传输通道均未知的情况下,仅由观察信号和少量的先验信息来提取有用信号[4-5],这对于具有复杂结构的机械系统的信号处理非常有利。BSS发展初期只能处理线性瞬时混合模型,并产生许多性能良好的算法[6],如快速独立成分分析(FastICA)法、信息极大化(Informax)法、自然梯度法、基于独立性的等变自适应分离(EASI)法等,但这种模型认为混合信号是源信号的线性叠加,并且不考虑传输通道的延迟效应,是一种理想化的模型。对于线性模型的改进则是考虑了源信号之间的非线性畸变,从而产生了非线性盲分离模型(NBSS)。文献[7]利用基于变分贝叶斯算法的NBSS对采集的轴承外圈故障信号进行分析,成功提取出轴承外圈故障特征信号。文献[8]认为传感器接收的信号为齿轮故障和轴承故障的非线性混合,并使用形态分量分析方法实现了两类故障的分离。NBSS相比于BSS更加符合实际情况,但处理方式也更加复杂和困难。

NBSS算法通常使用神经网络来拟合非线性混合的逆过程,但是基于神经网络的算法容易陷入局部最优解的问题。文献[9]提出利用PSO算法实现径向基函数神经网络的参数优化,进而实现非线性混合逆过程的逼近,仿真实验表明方法效果较好。基本的PSO算法存在粒子早熟和后期迭代效率不高的缺点,尤其是当解空间为非凸集时,容易在后期陷入局部极值点[10]。文献[10]提出基于遗传交叉因子的PSO算法,加快了收敛速度,并能有效避免粒子早熟问题。

本文提出一种基于改进PSO(Improved PSO,IPSO)的NBSS算法。该方法利用多层感知机(MLP)来拟合非线性混合的逆过程,并将分离信号的互信息最小作为PSO算法的优化目标,从而实现MLP中参数的优化。为了避免MLP参数优化过程陷入局部最优解,对适应度低的一部分粒子进行依概率的杂交和变异,从而使粒子群体在整个迭代过程中保持多样性,有效地避免了粒子早熟的问题。最后,通过仿真试验和薄板激励试验验证所提算法的有效性。

1 非线性盲源分离理论

NBSS的数学模型可以表示为

(1)

式中:St、Ut、Xt和Yt分别为源信号、观察信号(线性混合信号)、观察信号(非线性混合信号)和分离信号;Vt为中间变量;A和W分别为线性混合函数和线性解混函数;f和g分别是非线性混合和解混函数。混合系统和分离系统示意图如图1所示。

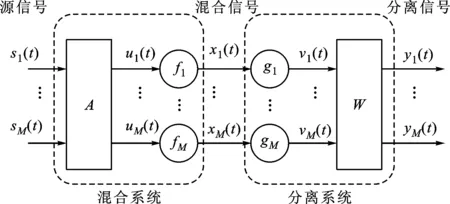
图1 非线性盲源分离混合系统和分离系统示意图

NBSS的目标就是找到合适的W和g,使得W=A-1,g=f-1,可得Yt=A-1f-1[f(ASt)]=ΛPSt,其中Λ和P分别为对角矩阵和置换矩阵。此时,分离信号除幅值和排列次序与源信号不同外,在信号的振动特征上将逼近源信号。

2 独立性测量

2.1 互信息

互信息的定义为[5]

(2)

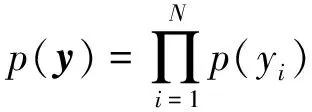
2.2 多层感知机

由于非线性混合函数f未知,在解混系统中需设计相应的非线性解混函数g。文献[11]利用MLP来逼近评价函数和系统的非线性函数,取得了良好的效果。本研究采用带一层隐藏层的MLP来逼近非线性混合的逆过程,MLP示意图如图2所示。

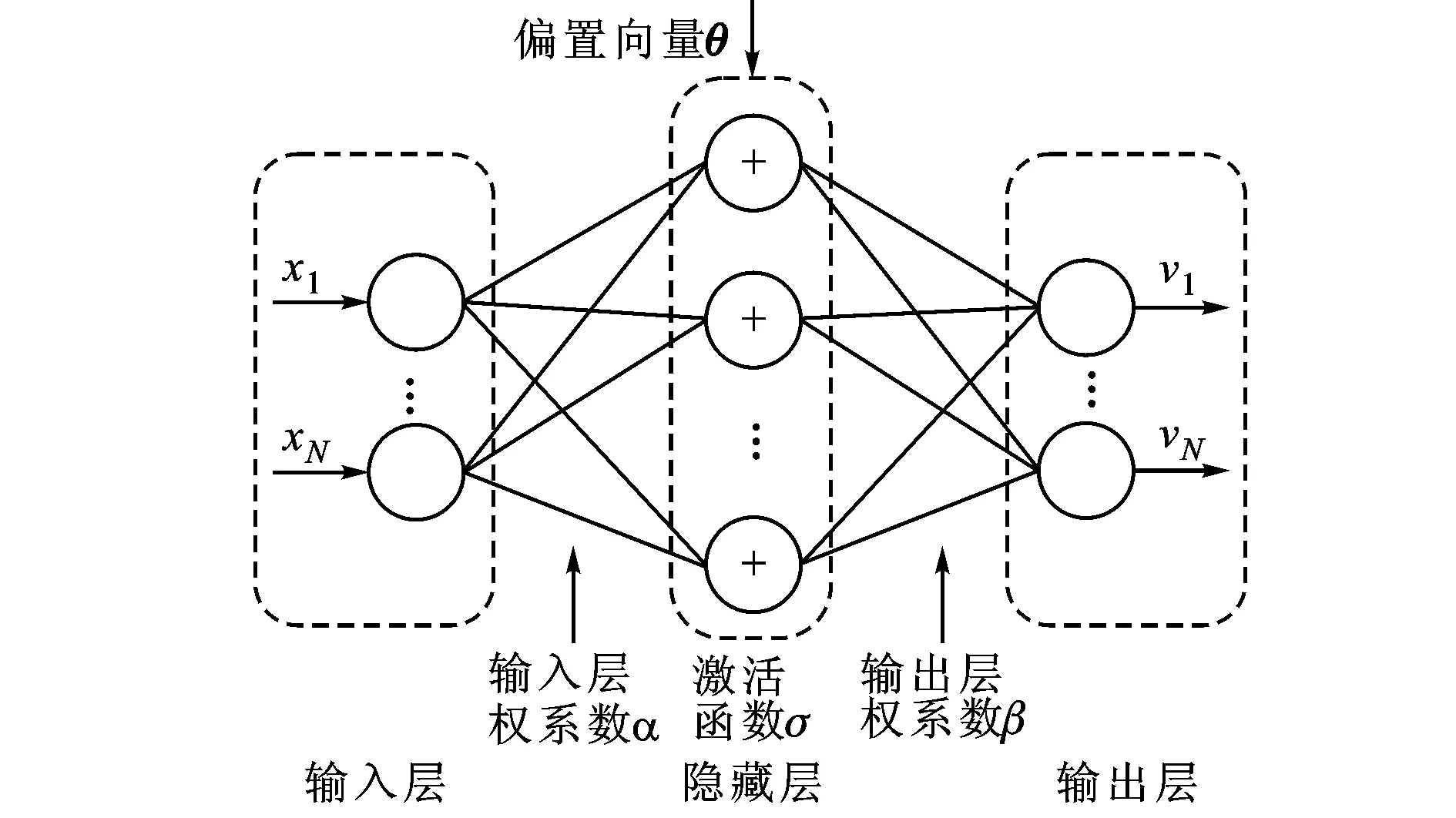
图2 多层感知机示意图

非线性解混过程为

v=βσ(αx+θ)

(3)

式中:α为输入层权系数;β为输出层权系数;σ为激活函数;θ为偏置向量。令线性解混矩阵为W,则分离信号为

y=Wv=Wβσ(αx+θ)

(4)

令γ=Wβ,则

y=γσ(αx+θ)

(5)

则分离信号的互信息为[12]

ln|detγ|-ln|detα|-H(x)

(6)

式中:H(x)为x的联合微分熵,仅与观察信号有关,与解混系统的参数无关,故优化分离矩阵时,可将H(x)作为常数。将H(yi)进行Edgeworth展开

(7)

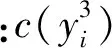
由互信息定义可知:当式(6)取得最小值时,意味着信号已经分离。式(6)可以作为PSO算法的适应度函数,其中共有3个参数γ、α和θ,通过优化这3个参数使式(6)取得最小值。

3 粒子群优化算法

PSO算法是一种启发式的优化算法,即在状态空间中对每一个寻优位置进行评估,最终得到最优位置,再从该位置进行搜索,直到获得最优的目标值。它具有通用性强、计算简单和全局优化的优点。

3.1 基本粒子群优化算法

1995年,文献[13]提出的PSO算法,将寻优问题类比做鸟群寻找栖息地。文献[14]通过引入收缩因子确保PSO算法的收敛性,称为标准粒子群(Canonical PSO, CPSO)。假设整个粒子群包含s个粒子,每个粒子代表了一个潜在的可行解。CPSO在D维搜索空间中,对于第k代的第i(1≤i≤s)个粒子的速度和位置更新表达式如下

vi(k+1)=χ{vi(k)+φ1c1[pi(k)-xi(k)]+

φ2c2[pg(k)-xi(k)]}

(8)

xi(k+1)=xi(k)+vi(k+1)

(9)

式中:χ=2/|2-φ-(φ2-4φ)1/2|称为收缩系数,φ=φ1+φ2,φ>4,一般取φ1=φ2=2.05,此时可得χ=0.729 8;xi和vi分别为第i个粒子的位置和速度;pi和pg分别为第i个粒子自身的历史最优位置和整个粒子群的历史最优位置;c1和c2为[0,1]之间均匀分布的随机变量。式(8)和式(9)称为进化公式。粒子的位置更新示意图如图3所示。关于PSO算法更多细节,文献[15]给出了详细的介绍。

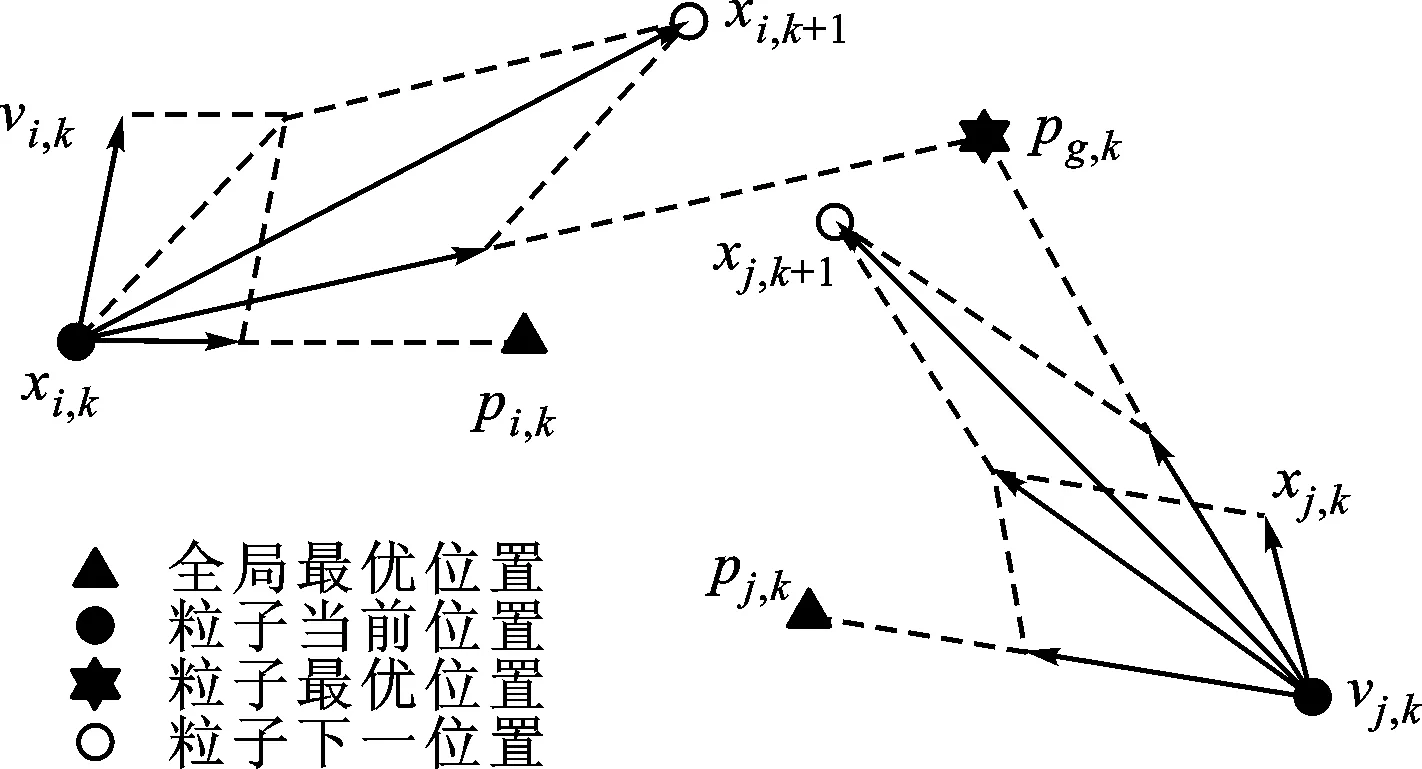
图3 粒子群更新示意图

3.2 改进粒子群优化算法

PSO算法虽然能够在整个解空间中搜索最优解,但仍易陷入局部最优解,即存在粒子早熟问题,从而丧失了种群多样性,致使群体中的大部分个体聚集在一个很小的范围内,这时种群已丧失了大范围搜索的能力。一种改善粒子早熟的方法是增大种群多样性,使粒子分布在一个较大的范围,增强PSO算法的全局搜索能力。

改善PSO算法粒子早熟的方法如下。在每次对粒子的位置和速度更新之后,按照其适应度的大小对粒子进行重新排序。由于PSO算法优化目标为分离信号互信息最小化,因此粒子对应的目标函数值越小,表明粒子的适应度较高。适应度较好的部分粒子直接进入下一代,适应度不好的部分进行杂交和变异操作,获取相同数量的子代。

设xi和xj为亲代,交叉的开始点和结束点m和n均随机产生,则交叉的操作即交换xi和xj第m和n维,即

(10)

交叉操作的示意图如图4a所示。交叉之后,计算xi和xj的适应度,如果交叉之后的粒子适应度高于交叉之前,则用交叉之后的粒子替换交叉之前的粒子;反之,则保留原有粒子。

变异的操作示意图如图4b所示。设xk为需要变异的粒子,变异的开始点l随机产生,则xk的第l维至第N维随机产生。

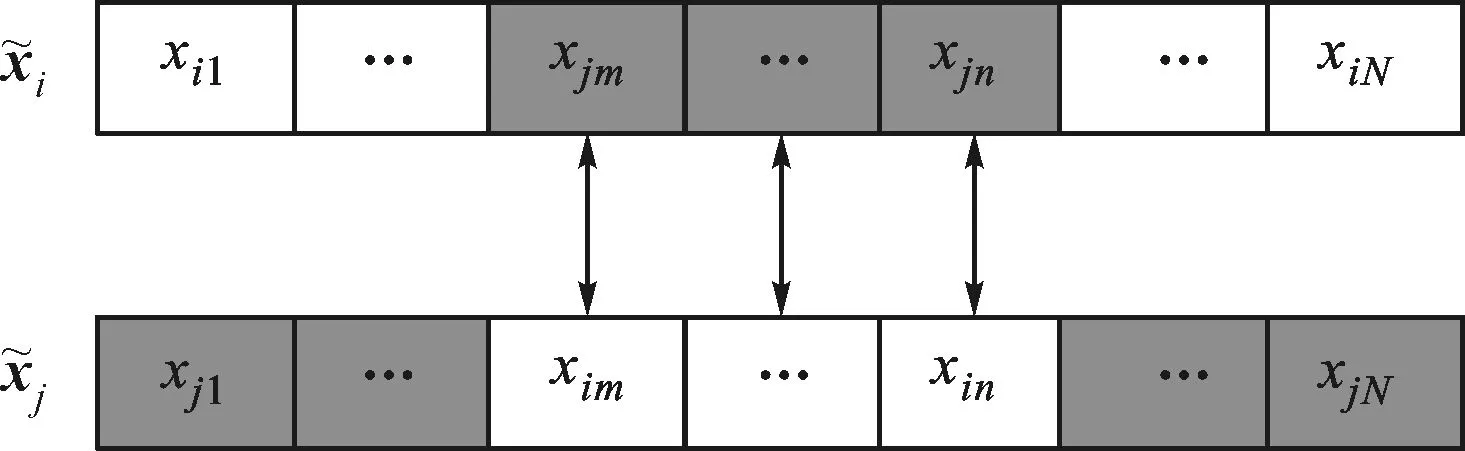
(a)交叉操作

(b)变异操作
图4 粒子的交叉和变异操作示意图

4 算法验证

为了验证提出算法的正确性和有效性,进行如下的数值试验和薄板激励试验验证。通过对比不同算法分离信号的时域波形及其频谱,评价算法的优劣,并计算分离信号与源信号之间的相关系数

(11)

式中:rij是第i个源信号si和第j个分离信号yj之间的相关系数,也即源信号和分离信号相关矩阵r的第(i,j)个元素。

4.1 数值试验验证

源信号为

(12)

混合矩阵为

(13)

非线性混合方程为

(14)

采样频率fs=10 kHz,粒子群参数φ1=2.05,φ2=2.05,χ=0.729 8,粒子群的规模N=50,最大迭代次数M=2 500。多层感知机中间层神经元个数设置为4,则α的维数为4×4,β的维数为4×4,θ的维数为4×1,需要优化的参数共36个,故每个粒子的维数为36。源信号的波形及其频谱如图5所示,4个源信号分别为低频正弦信号、高频正弦信号、幅值调制信号和白噪声信号,信号幅值用a表示。经过非线性混合后的混合信号的波形及其频谱如图6所示。

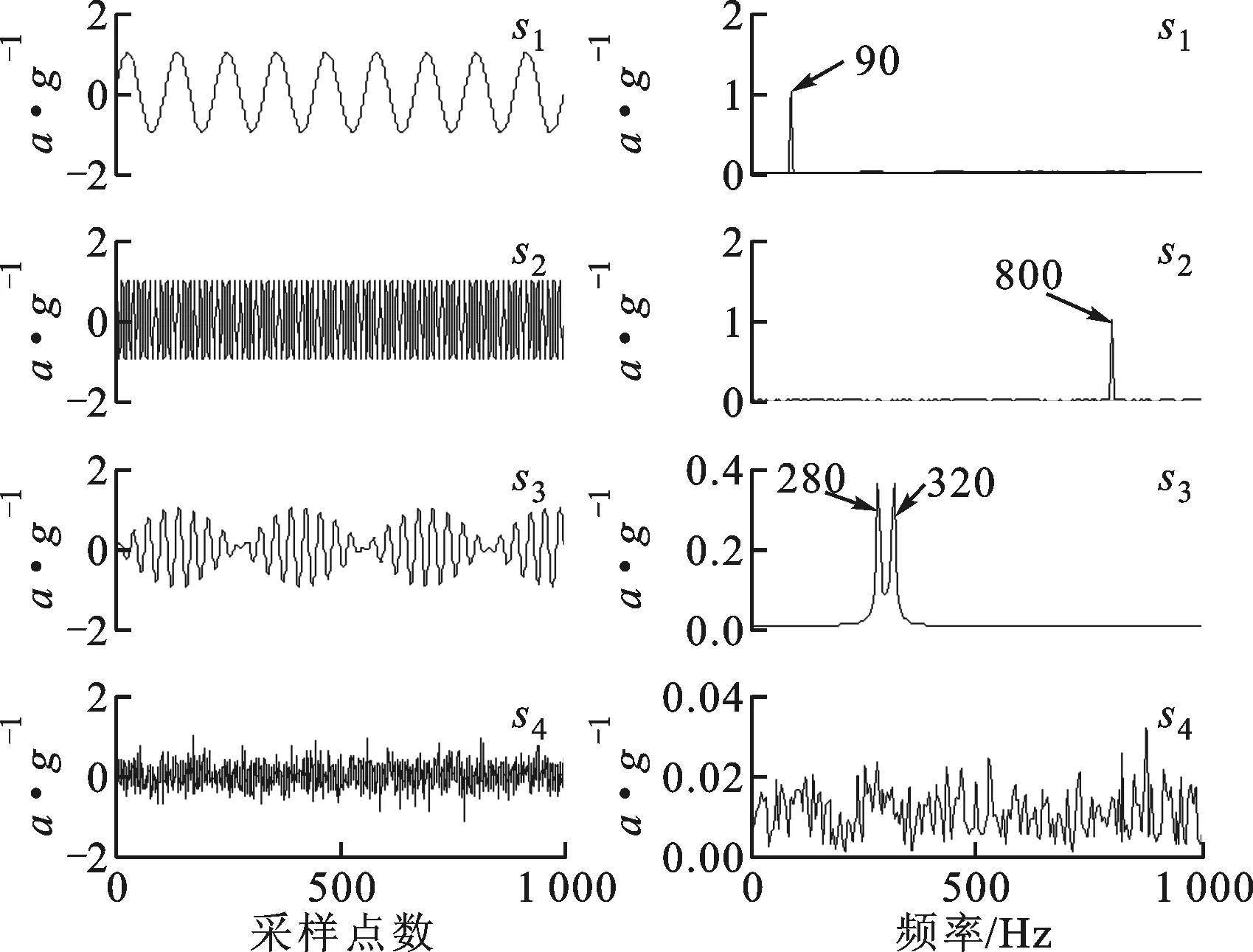
(a)时域波形 (b)频谱图5 源信号的时域及频谱特性

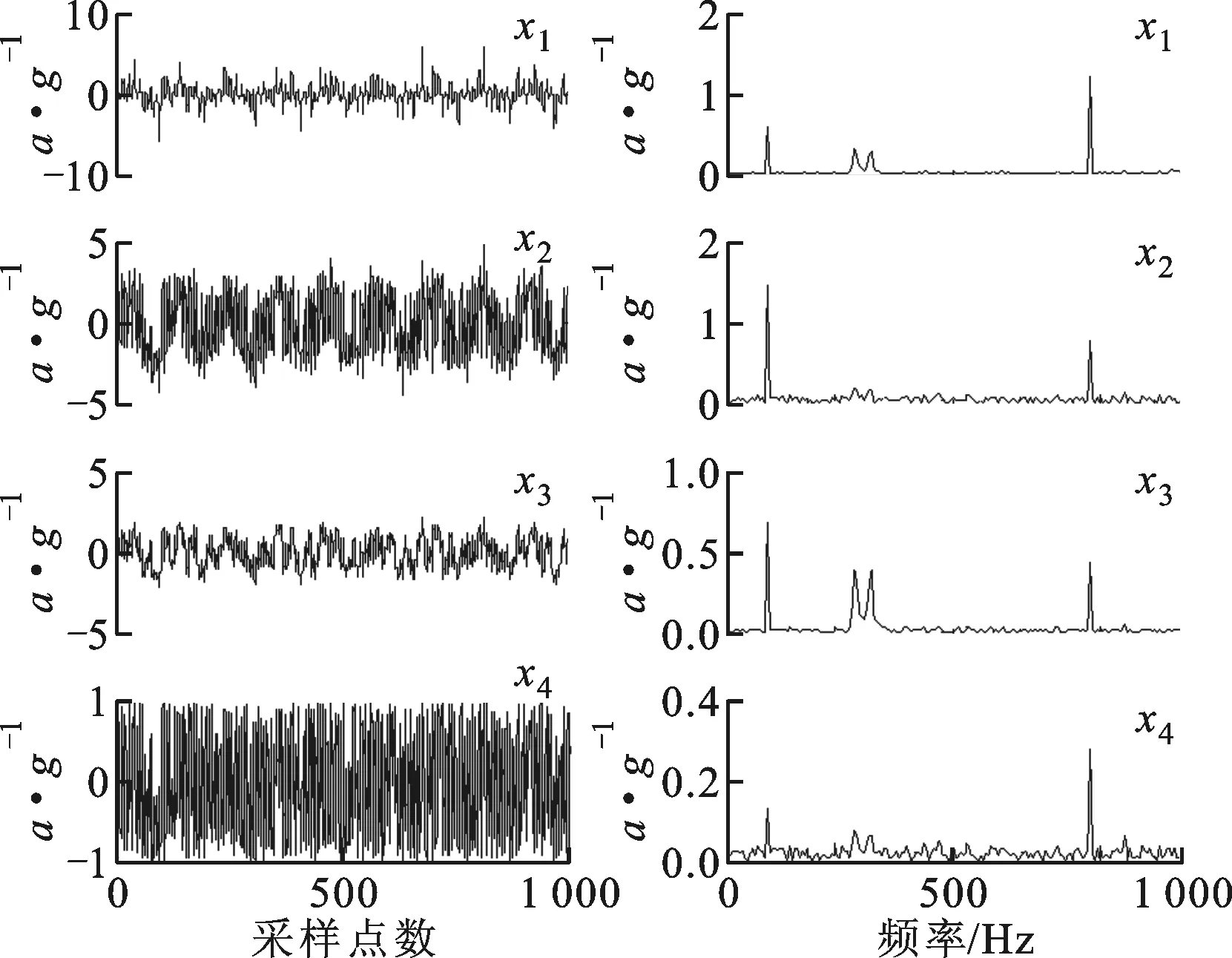
(a)时域波形 (b)频谱图6 混合信号的时域及频谱特性

采用快速独立成分分析(ICA)算法对混合信号进行分离,得到4个分离信号的时域及频谱如图7所示。由于信号是非线性混合的,线性分离算法得到的结果较差,而且在不同的分离信号中存在较为严重的频率交叉现象。如在第3个分离信号中,除含有280 Hz和320 Hz组成的调制信号外,还含有频率为90 Hz的低频振动成分和频率为800 Hz的高频振动成分,给结果的分析带来困难。这表明线性分离算法在处理非线性混合信号时性能欠佳。

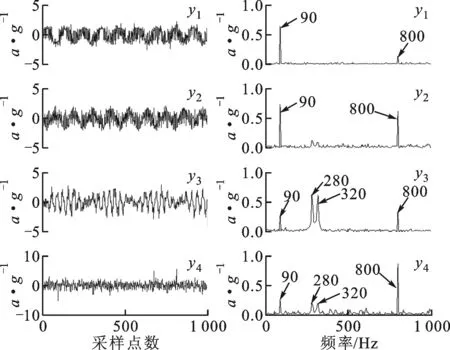
(a)时域波形 (b)频谱图7 ICA分离结果的时域及频谱特性

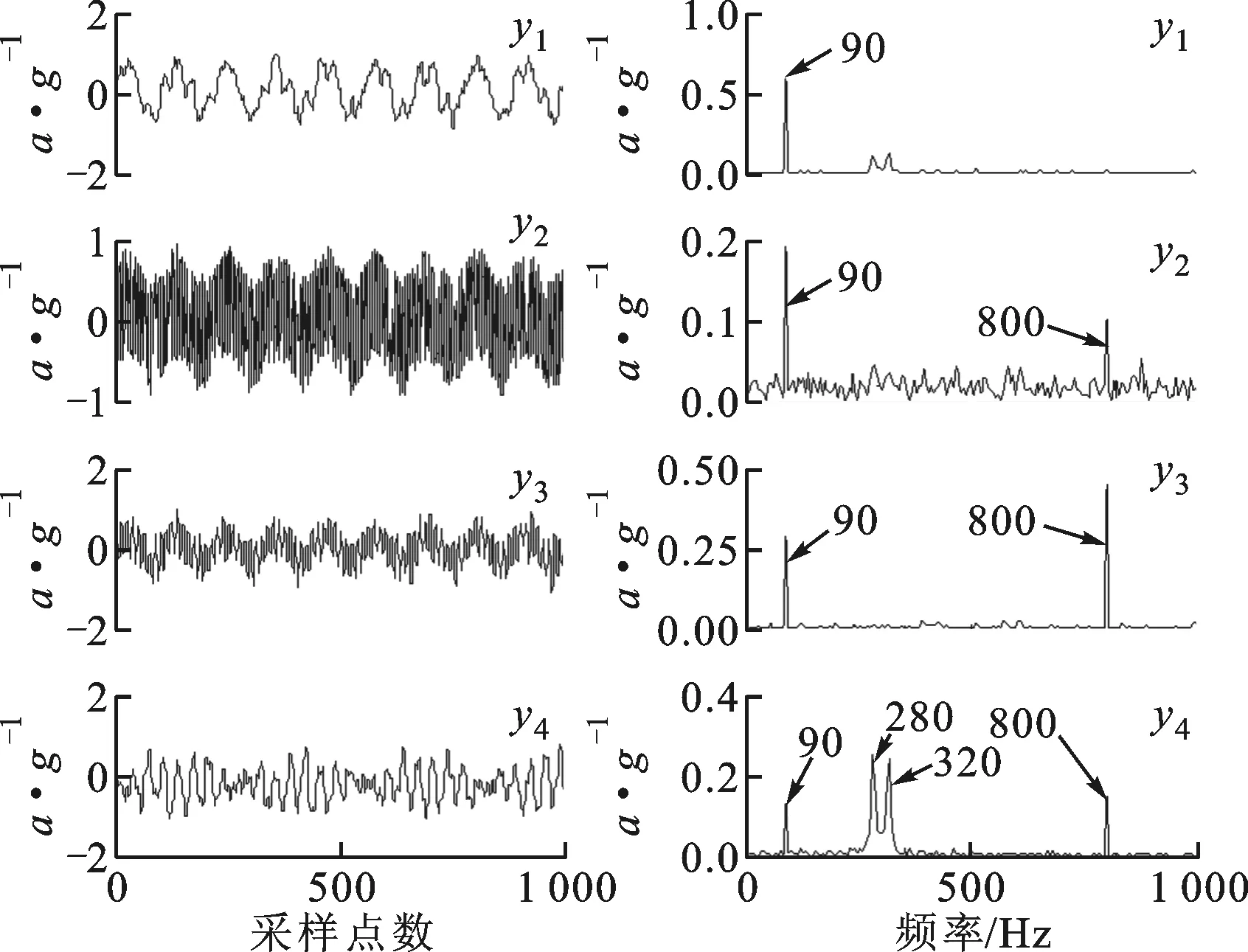
(a)时域波形 (b)频谱图8 NBSS-CPSO分离结果的时域及频谱特性

采用基于标准粒子群的非线性盲源分离(NBSS-CPSO)算法,得到分离信号的时域及频谱如图8所示。从图8中可以看出,第1个、第3个和第4个信号分别对应低频正弦、高频正弦和幅值调制信号。由于CPSO算法存在粒子早熟现象,使得粒子群体过早地收敛到局部极值,使得信号分离不彻底,信号之间同样存在较为严重的频率交叉现象,在第3和第4个分离信号中可以体现。NBSS-CPSO算法的分离结果较线性分离算法好,但仍然不够理想。

采用提出的基于改进粒子群的非线性盲源分离(NBSS-IPSO)算法进行处理,得到的分离信号的时域及频谱如图9所示。从图9可以看出:第1个分离信号对应源信号中的低频正弦成分,虽然仍包含有高频振动成分,但已较为微弱;第2个分离信号对应源信号中的幅值调制信号,除特征频率280 Hz和320 Hz外,其他的噪声频率成分也已经十分微弱;第3个分离信号对应高频正弦信号,分离效果比较理想;第4个信号为噪声信号。由此可知,NBSS-IPSO算法的分离效果明显优于其他两种算法。

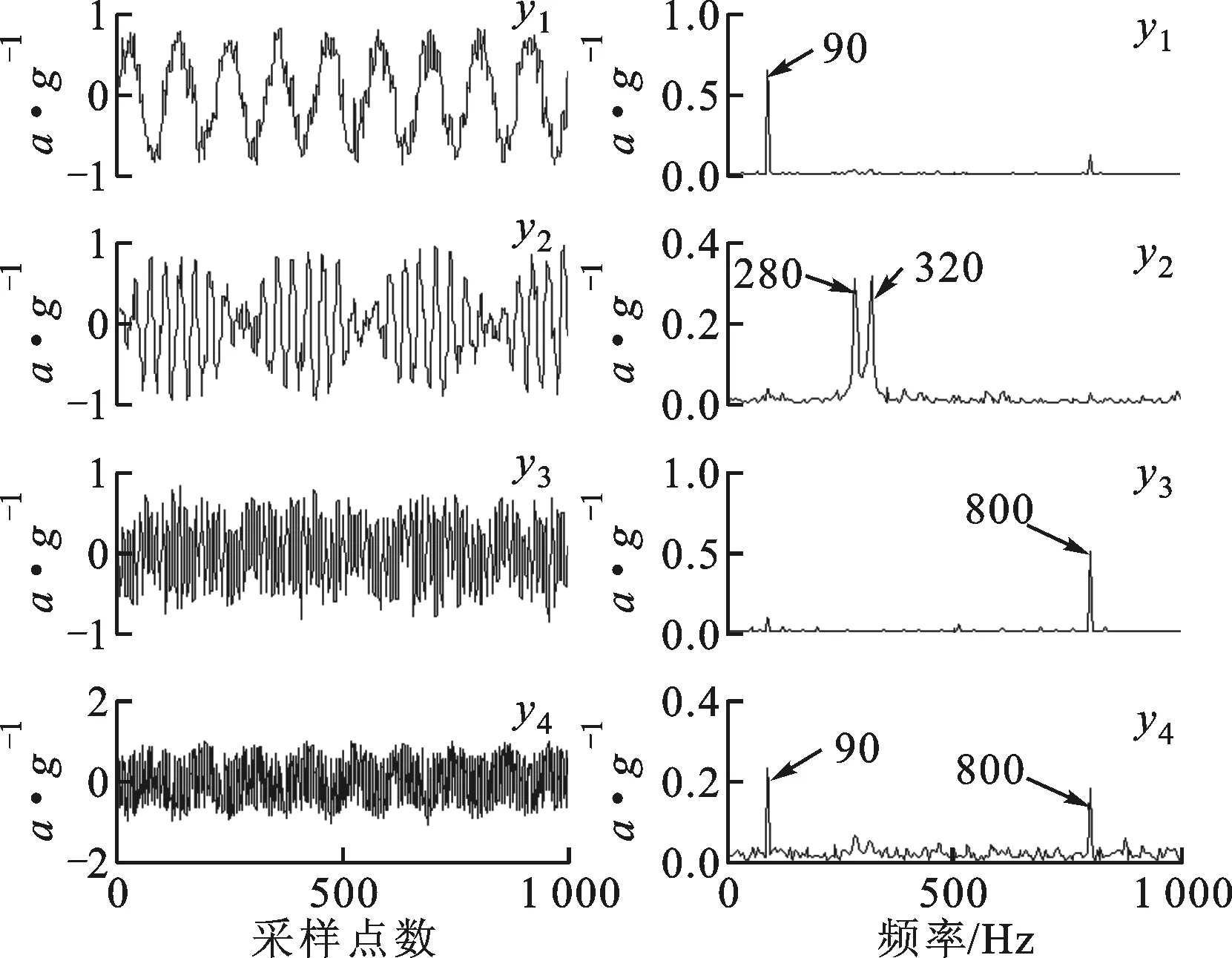
(a)时域波形 (b)频谱图9 NBSS-IPSO分离结果的时域及频谱特性

两种基于PSO的NBSS算法的互信息收敛曲线如图10所示。从图10中可以看到,在迭代次数约为200时,NBSS-CPSO算法已基本收敛,其互信息值已基本保持不变,约为0.705,而NBSS-IPSO算法的互信息的最终值为0.281,表明NBSS-IPSO算法效果更好。利用ICA算法得到的分离信号与源信号的相关系数矩阵为

(15)

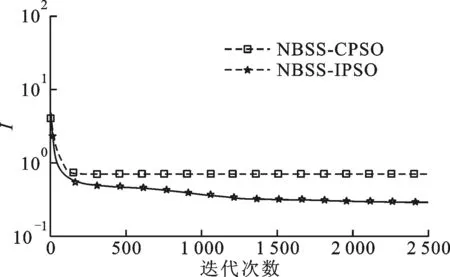
图10 两种基于PSO的算法互信息收敛曲线的对比

利用NBSS-CPSO算法,得到的分离信号与源信号的相关系数矩阵为

(16)

利用NBSS-IPSO算法,得到的分离信号与源信号的相关系数矩阵为

(17)

由式(15)可知,利用ICA算法得到的分离信号和源信号的相关系数矩阵中,只有一个大于0.8,而且除第3行外,均存在两个较为接近的数值,表明信号分离不彻底,存在信号之间的干扰现象。由式(16)可知,利用NBSS-CPSO算法得到的相关系数矩阵结果较ICA算法好,每行中的最大值基本都在0.8以上。由式(17)可知,采用NBSS-IPSO算法得到的相关系数矩阵除第4个噪声信号为0.841 3之外,其余分离信号与相应源信号的相关系数均在0.9以上,表明NBSS-IPSO算法的分离效果最好。

4.2 板激励试验

通过板激励试验来验证提出算法的正确性和有效性。试验采用2个激振器作为激励源,即源信号,激振器和阻抗头均为PCB公司生产,型号分别为K2004E01和288D01。采用2个信号发生器产生信号作为激振器的输入,2个信号发生器型号分别为泰克AFG3000C和安捷伦33500。利用4个PCB加速度传感器接收振动信号作为观察信号,传感器的参数如表1所示。信号采集装置为HBM公司生产的GEN2i高速数据记录仪,通道数为64。采样频率为4 096 Hz,试验中激励源和传感器的位置如图11所示,试验现场实物图如图12所示。

表1 传感器参数表

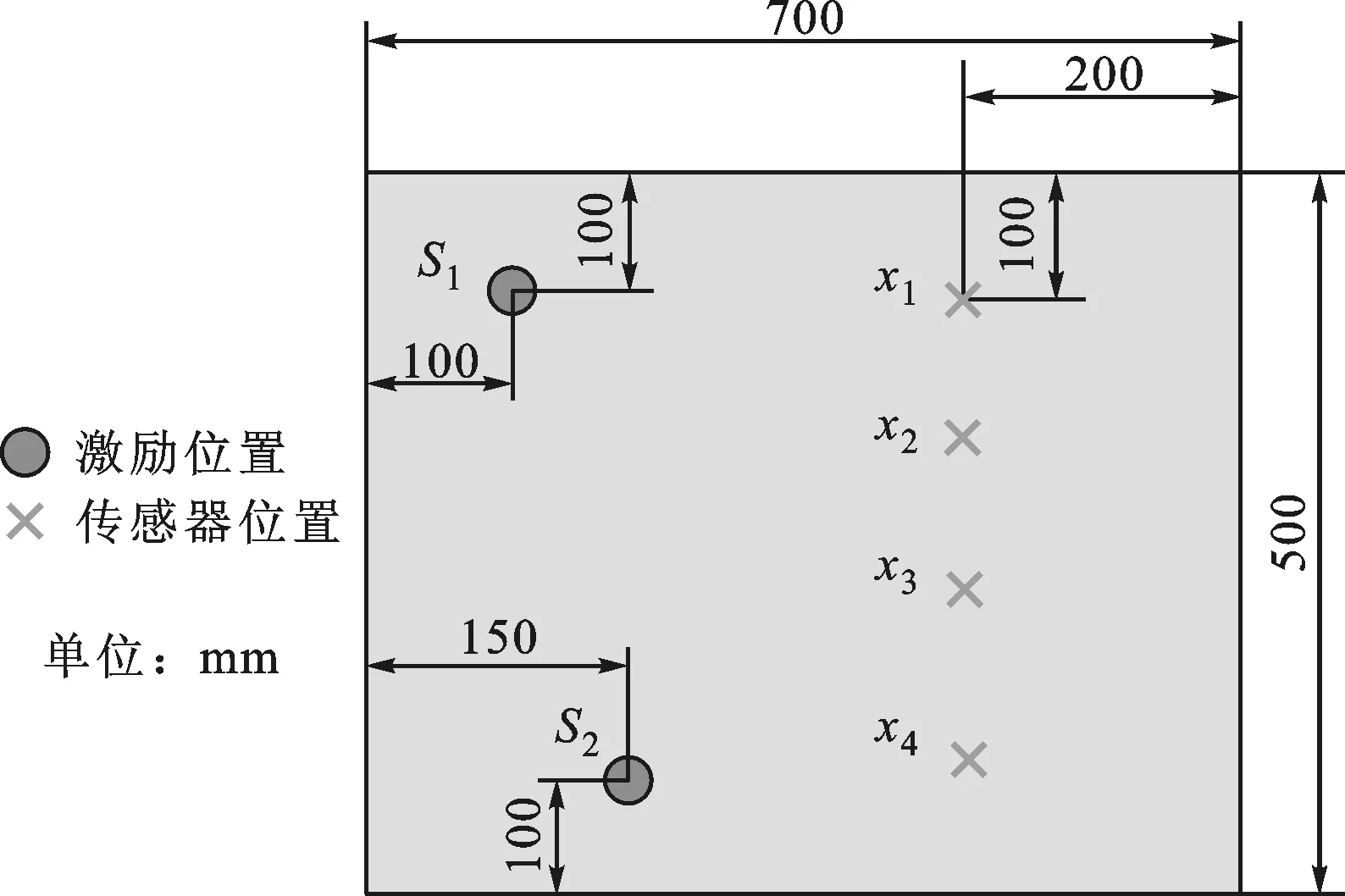
图11 激励源与传感器位置分布

图12 板激励现场试验图

板激励试验的2个源信号分别为脉冲信号和正弦信号,其时域和频谱如图13所示。从图13中可知,脉冲信号的基频为62 Hz,频谱图中含有基频及其倍频成分,正弦信号的频率为76 Hz。选取图11中的x1、x2和x3作为混合信号进行分离,混合信号的时域和频谱如图14所示。从图14中可知,3个混合信号均为2个源信号的未知混合,从其时域波形不能分辨出源信号,而频域波形中也为2个源信号的混合,给源信号的识别造成困难。

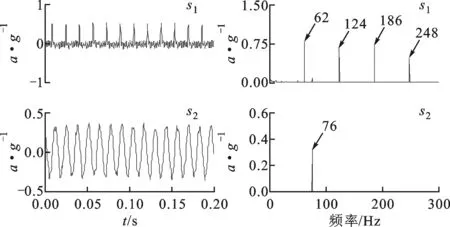
(a)时域波形 (b)频谱图13 板激励试验源信号时域及频谱特性

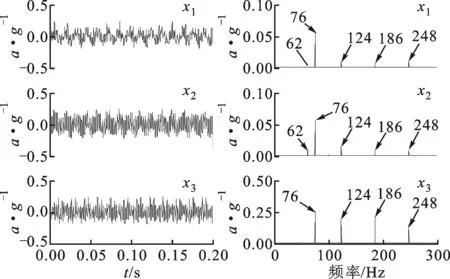
(a)时域波形 (b)频谱图14 板激励试验混合信号时域及频谱特性

采用ICA方法对混合信号进行分离,得到的结果如图15所示。从图15b可以看出:第1个分离信号可认为是冲击信号,但是含有较大的正弦频率成分76 Hz,其时域图中也不能看出明显的冲击成分;第2个分离信号为正弦信号,但含有较大的噪声成分。因此可以看出,ICA算法的分离效果并不理想。

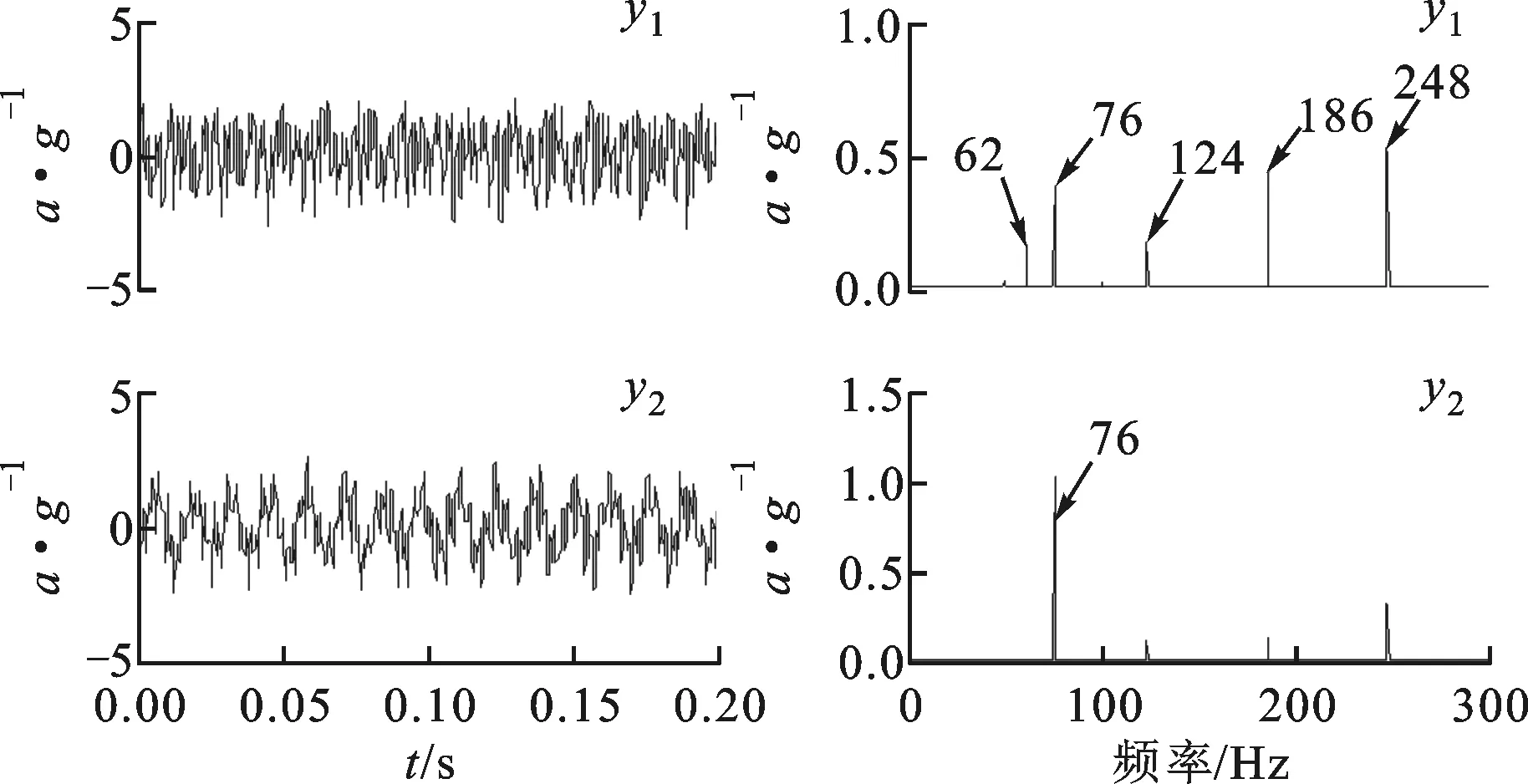
(a)时域波形 (b)频谱图15 ICA算法分离信号时域及频谱特性

使用NBSS-CPSO算法对混合信号进行分离,得到的分离信号如图16所示。从图16中可以看出:第1个分离信号的主要频率为76 Hz,应为正弦信号,但仍有较大的干扰噪声;第2个分离信号为脉冲信号,含有冲击成分,冲击间隔Δt1=0.016 1 s,即冲击频率f=61.97 Hz,接近源信号中脉冲信号的冲击频率62 Hz。

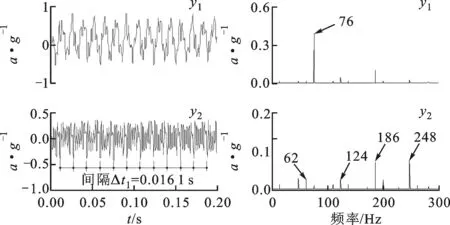
(a)时域波形 (b)频谱图16 NBSS-CPSO算法分离信号时域及频谱特性

利用本文提出的NBSS-IPSO算法对混合信号进行分离,得到的分离信号如图17所示。从图17中可以看出,第1个分离信号是频率为76 Hz的正弦信号,第2个分离信号为脉冲信号。对比图16a和图17a可知,正弦成分和冲击成分更加清晰,而冲击信号的冲击间隔Δt2=0.0161 s,计算得到冲击频率f=61.98 Hz,接近源信号中脉冲信号的冲击频率62 Hz,频谱图含有62 Hz频率及其倍频成分,表明源信号已得到较好的分离。

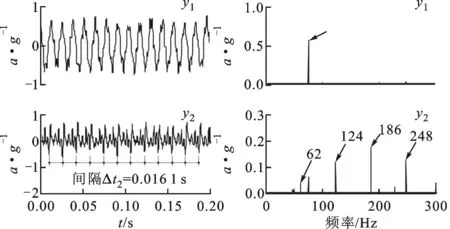
(a)时域波形 (b)频谱图17 NBSS-IPSO算法分离信号时域及频谱特性

两种基于PSO的NBSS算法互信息收敛曲线如图18所示。由于引入PSO算法,两种算法的收敛速度都比较快,但NBSS-IPSO算法收敛的最终值较小,表明本文所提的算法效果较好。

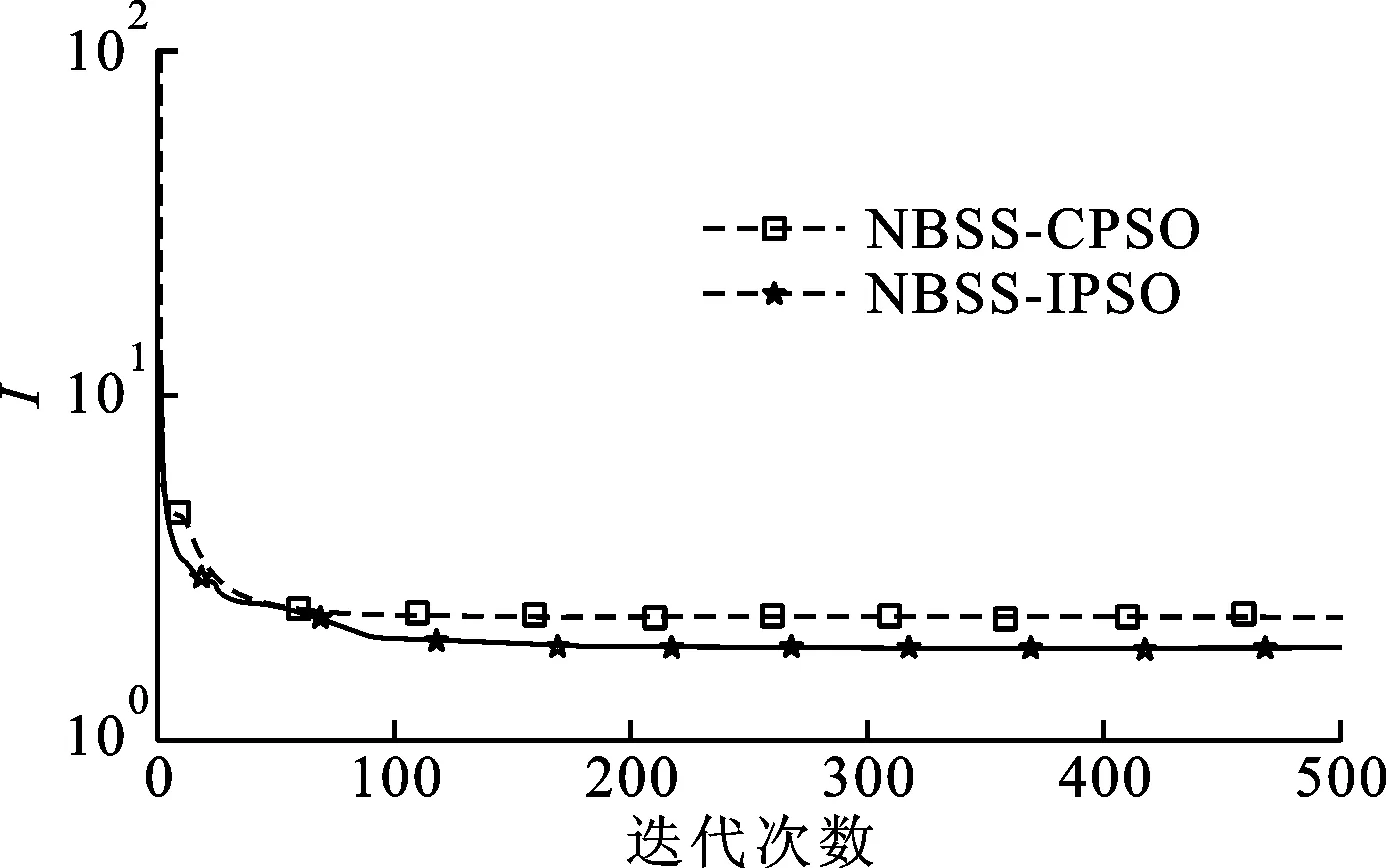
图18 两种粒子群算法互信息收敛曲线的对比

5 结 论

NBSS能够模拟信号在复杂机械结构传播过程中的非线性失真,较线性BSS更加符合实际情况。本文采用MLP逼近非线性混合的逆过程,以分离信号的互信息最小为优化目标,并采用IPSO算法对该过程中的参数进行优化,实现了非线性混合信号的分离。数值试验和板激励试验的分离结果都证明了本文算法的正确性和有效性。从分离结果可以看出,本文算法的分离精度优于线性BSS和基于CPSO优化的NBSS算法。本文方法可以从非线性混合机械信息中提取纯净的独立源信息,为机械系统的监测诊断和振动噪声溯源提供科学依据和关键技术。

[1] JARDINE A K S, LIN D, BANJEVIC D. A review on machinery diagnostics and prognostics implementing condition-based maintenance [J]. Mechanical Systems and Signal Processing, 2006, 20(7): 1483-1510.

[2] CHENG W, LEE S, ZHANG Z S, et al. Independent component analysis based source number estimation and its comparison for mechanical systems [J]. Journal of Sound and Vibration, 2012, 331(23): 5153-5167.

[3] 成玮, 何正嘉, 张周锁. 基于独立分量分析的壳体结构振源数目估计方法 [J]. 机械工程学报, 2014, 50(19): 73-79. CHENG Wei, HE Zhengjia, ZHANG Zhousuo. Vibration source number estimation of shell structures based on independent component analysis [J]. Journal of Mechanical Engineering, 2014, 50(19): 73-79.

[4] HAILE M A, DYKAS B. Blind source separation for vibration-based diagnostics of rotorcraft bearings [J/OL]. Journal of Vibration and Control, 2015 [2015-12-22]. http: ∥jvc.sagepub.com/content/early/2015 /01/21/1077546314566041.full.pdf+html.

[5] 陆建涛, 成玮, 訾艳阳, 等. 变步长等变自适应盲源分离算法 [J]. 西安交通大学学报, 2015, 49(12): 83-89. LU Jiantao, CHENG Wei, ZI Yanyang, et al. Variable step-size algorithm for equivariant adaptive separation via independence [J]. Journal of Xi’an Jiaotong University, 2015, 49(12): 83-89.

[6] 王法松, 李宏伟, 沈远彤. 非线性盲源分离的原理及算法综述 [J]. 信号处理, 2005, 21(3): 282-288. WANG Fasong, LI Hongwei, SHEN Yuantong. An overview on nonlinear blind source separation: theory and algorithms [J]. Signal Processing, 2005, 21(3): 282-288.

[7] 范涛, 李志农, 岳秀廷. 基于变分贝叶斯算法和MLP网络的后非线性混合盲源分离方法研究 [J]. 振动与冲击, 2010, 29(6): 21-24. FAN Tao, LI Zhinong, YUE Xiuting. Post_nonlinear blind separation of the source signals based on variational Bayesian theory and MLP [J]. Journal of Vibration and Shock, 2010, 29(6): 21-24.

[8] LI Z S, PENG Z. A new nonlinear blind source separation method with chaos indicators for decoupling diagnosis of hybrid failures: a marine propulsion gearbox case with a large speed variation [J/OL]. Chaos, Solitons & Fractals, 2015 [2015-12-22]. http: ∥www. sciencedirect.com/science/article/pii/S0960077915003 021.

[9] TAKUYA K, KENYA J. A nonlinear blind source separation system using particle swarm optimization algorithm [J]. Journal of Signal Processing, 2013, 17(6): 255-264.

[10]李季, 孙秀霞, 李士波, 等. 基于遗传交叉因子的改进粒子群优化算法 [J]. 计算机工程, 2008, 34(2): 181-183. LI Ji, SUN Xiuxia, LI Shibo, et al. Improved particle swarm optimization based on genetic hybrid genes [J]. Computer Engineering, 2008, 34(2): 181-183.

[11]TABLE A, JUTTEN C. Source separation in post-nonlinear mixtures [J]. IEEE Trans on Signal Processing, 1999, 47(10): 2807-2820.

[12]LI W, YANG H Z. A non-linear blind source separation method based on perceptron structure and conjugate gradient algorithm [J]. Circuits Syst Signal Process, 2014, 33(11): 3573-3590.

[13]KEMNDY J, EBERHART R C. Particle swarm optimization [C]∥Proceeding of IEEE International Conference on Neutral Networks. Piscataway, NJ, USA: IEEE, 1995: 1942-1948.

[14]CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space [J]. IEEE Trans on Evolutionary Computation, 2002, 6(1): 58-72.

[15]CHOOSAK P. A particle swarm optimization for the vehicle routing problem [D]. Kinston, USA: University of Rhode Island, 2014.

[本刊相关文献链接]

陆建涛,成玮,訾艳阳,等.变步长等变自适应盲源分离算法[J].2015,49(12):83-89.[doi:10.7652/xjtuxb201512014]

徐光华,张锋,谢俊,等.稳态视觉诱发电位的脑机接口范式及其信号处理方法研.2015,49(6):1-7.[doi:10.7652/xjtuxb201506001]

熊涛,江桦,崔鹏辉,等.应用基扩展模型的混合信号单通道盲分离算法.2015,49(6):60-66.[doi:10.7652/xjtuxb201506 010]

刘进,李赞,高锐.低信噪比下采用广义随机共振的能量检测算法.2015,49(6):27-32.[doi:10.7652/xjtuxb201506005]

郝雯洁,齐春.一种鲁棒的稀疏信号重构算法.2015,49(4):98-103.[doi:10.7652/xjtuxb201504016]

孙锦华,韩会梅.低信噪比下时频联合的载波同步算法.2015,49(2):62-68.[doi:10.7652/xjtuxb201502011]

唐成凯,廉保旺,张玲玲.卫星通信系统双向中继转发自干扰消除算法.2015,49(2):74-79.[doi:10.7652/xjtuxb201502 013]

王静,黄建国,侯云山.采用峰值平均功率比的低信噪比水下多目标检测方法.2012,46(2):124-129.[doi:10.7652/xjtuxb201202021]

蔡改改,陈雪峰,陈保家,等.利用设备响应状态信息的运行可靠性评估.2012,46(1):108-113.[doi:10.7652/xjtuxb2012 01020]

(编辑 杜秀杰)

Nonlinear Blind Source Separation Combining with Improved Particle Swarm Optimization

(State Key Laboratory for Manufacturing System Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

The traditional nonlinear blind source separation (NBSS) algorithms often fall across the problem of local optimal solution to lead a lower separation precision. An NBSS algorithm based on improved particle swarm optimization (PSO) is proposed, where the multilayer perception (MLP) is used to fit the inverse of the nonlinear mixed process, and the mutual information between separated signals is regarded as the optimization objective (Fitness function of PSO) to realize the optimization of parameters in MLP. However, the canonical PSO algorithms usually suffer from particle premature problems and are easy to get into local optimal solution. Thus crossover and mutation operations are applied to the particles with lower fitness according to probability mechanism to efficiently increase the diversity of the particles, and the premature problem of canonical PSO is solved. The simulations and experiments show that compared with the linear blind source separation algorithm and the NBSS algorithm based on canonical PSO, the proposed algorithm enables to extract pure independent source information from mechanical information with nonlinear mixing and improve the separation precision of nonlinear mixed signals.

nonlinear blind source separation; particle swarm optimization; particle premature; crossover and mutation

2016-01-04。 作者简介:陆建涛(1990—),男,博士生;成玮(通信作者),男,副教授。 基金项目:国家自然科学基金资助项目(51305329);中国博士后科学基金资助项目(2013M532032,2014T70911);教育部高等学校博士学科点专项科研基金资助项目(20130201120040)。

时间:2016-03-11

10.7652/xjtuxb201606003

TH17

A

0253-987X(2016)06-0015-08

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160311.1719.008.html