考虑边缘接触的弧齿锥齿轮有限元接触分析

侯祥颖,方宗德

(西北工业大学机电学院,710072,西安)



考虑边缘接触的弧齿锥齿轮有限元接触分析

侯祥颖,方宗德

(西北工业大学机电学院,710072,西安)

针对弧齿锥齿轮轻质重载的特点,利用有限元方法的批处理功能进行了考虑边缘接触的轮齿接触分析,定量讨论了边缘接触随载荷增加时的变化规律。根据考虑边缘接触的几何接触分析,将齿轮从进入啮合到退出啮合分成若干步进行计算,每一步的计算结果连接起来用于描述整个啮合的过程。以一对弧齿锥齿轮为例,经过不同载荷条件下考虑边缘接触的定量分析,提取出接触应力、接触印痕、接触路径,并与几何接触分析和承载接触分析结果进行了对比,三者吻合度较好。对比结果证明,通过有限元法分析可以较精确地确定齿轮发生边缘接触时的载荷临界值及边缘接触位置,得出边缘接触会导致接触应力急剧增大、接触路径延长、接触区域面积变大的结果,通过定量计算、比较各项参数指标得出变化规律。

弧齿锥齿轮;边缘接触;接触应力;接触印痕;有限元方法

弧齿锥齿轮是航空动力传递过程中的关键部件,随着航空技术的发展,航空弧齿锥齿轮越来越向着高速、重载方向发展。弧齿锥齿轮副靠齿面啮合传递动力,但当载荷增大到一定程度、调整参数不合理或安装出现误差时会引起边缘接触。边缘接触会影响齿面啮合性能,产生噪声和振动,因此边缘接触分析成为齿面接触分析中不可缺少的一环。

高建平等提出了描述螺旋锥齿轮边缘接触的方法,得到了考虑边缘接触的传动误差曲线和接触区域图[1]。方宗德等进行了考虑边缘接触的弧齿锥齿轮承载接触分析,求解了边缘接触条件下齿轮的承载传动误差和载荷分配等[2]。Gonzalez-Perez等以直齿轮为例,用赫兹接触理论与有限元计算结果进行了相互验证[3]。Wang Peiyu等用有限元方法分析了弧齿锥齿轮的动态啮合性能及冲击等[4]。Wang Huanmei等对弧齿锥齿轮的热应力变化进行了分析和讨论[5]。Mermoz等提出了一种新方法来优化弧齿锥齿轮齿面形貌[6]。唐进元等采用有限元方法对螺旋锥齿轮进行了接触分析,讨论了齿轮接触刚度计算方法、应力变化、振动冲击等[7-8]。Chen讨论了弧齿直齿轮网格加密方法及不同参数下的接触椭圆、接触应力和传动误差的变化情况[9]。Litvin以减振降噪为目标设计了一对弧齿锥齿轮,并进行了有限元仿真和试验验证,得出接触应力在大小轮齿顶处比较大的结果[10]。Wu研究了啮合刚度与驱动轮齿数和载荷之间的关系[11]。Alfonso等分别画出了弧齿圆柱齿轮和面齿轮应力曲线,指出边缘接触存在[12-13]。

本文根据以上研究,利用较为成熟的有限元软件ABAQUS进行了轮齿接触分析,并以一对弧齿锥齿轮为例,在有限元网格模型[14]的基础上,根据几何接触分析(TCA)仿真结果,将齿轮从进入啮合到退出啮合划分成多个位置,从而实现了多个位置的批处理运行和后处理运算。这种静态批处理分析方法忽略了转动时产生的惯性力,可与承载接触分析(LTCA)结果比较。计算结果验证了有限元计算的可靠性,并为LTCA做出了补充,可准确判断出特定载荷下边缘接触发生的位置及应力分布等,以期为弧齿锥齿轮的齿面设计及接触性能研究提供参考。

弧齿锥齿轮齿面形状复杂,齿面微观形状由具体加工参数确定,所以本文仅针对一组特定几何参数和加工参数对弧齿锥齿轮进行讨论和分析。

1 齿轮参数

一对航空弧齿锥齿轮的基本参数如表1所示。

根据表1参数和文献[14]方法建立起一对弧齿锥齿轮的有限元模型。当载荷过大时,弧齿锥齿轮的实际重合度可能会增大到3左右,为了保证计算的准确度,本文均采用七齿模型,并以中间齿为研究对象,考察轮齿的啮合过程。

ABAQUS软件显示的一对弧齿锥齿轮的有限元网格如图1所示。针对该弧齿锥齿轮分别进行了不考虑边缘接触的TCA分析和考虑边缘接触的TCA分析[15-16],由此得到的大轮接触路径及齿轮副传动误差如图2、图3所示。

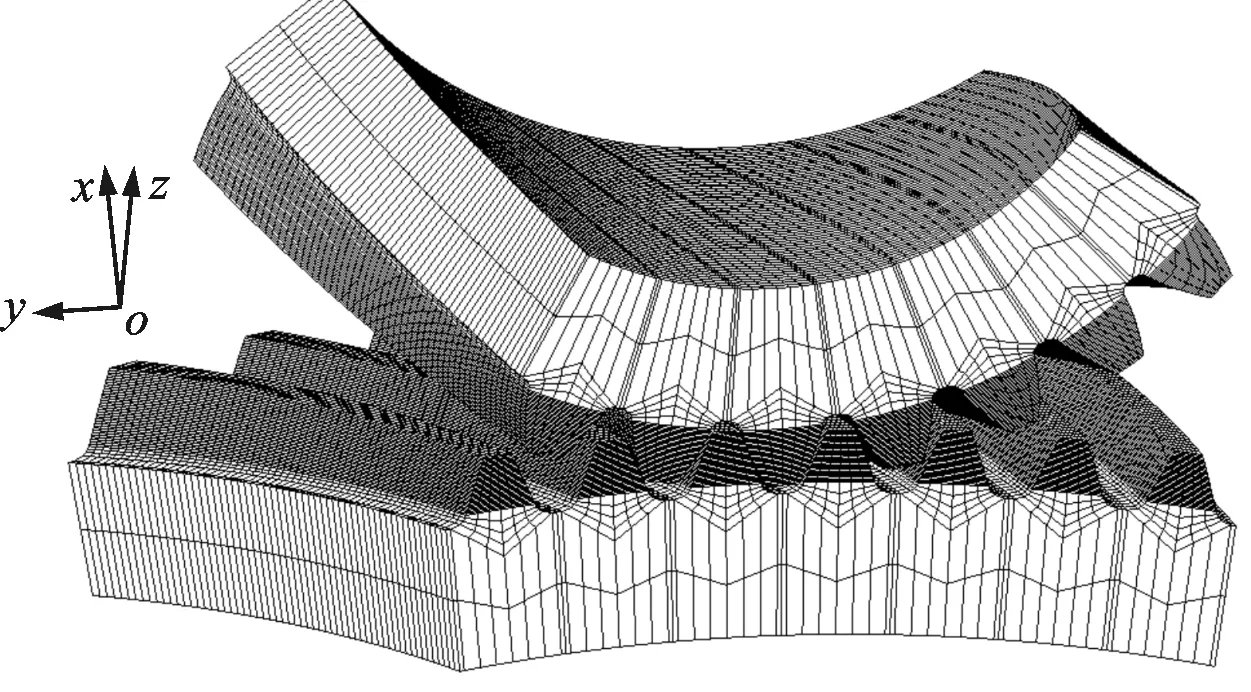
图1 一对弧齿锥齿轮有限元模型

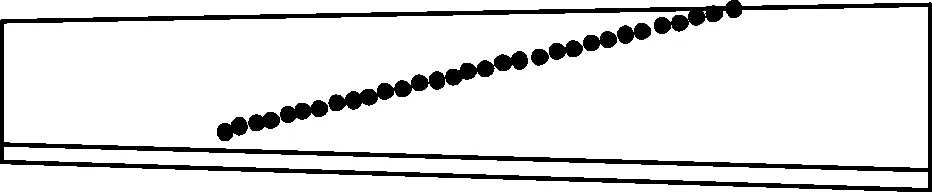
(a)无边缘接触

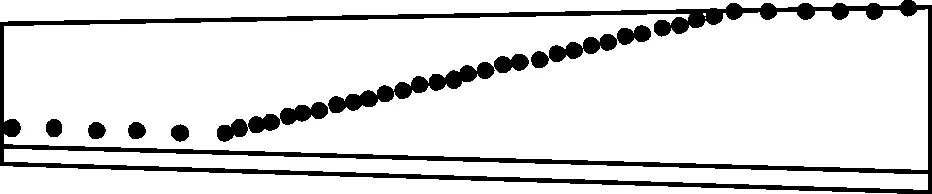
(b)有边缘接触图2 大轮齿面接触路径

2 有限元计算方法

使用静态分析方法对轮齿接触进行了分析。利用有限元软件的批处理接口、采用批处理编程建立起一组输入(input)文件,每个文件对应于一个接触位置,并为图2中划分的每个接触点位置处建立一对弧齿锥齿轮模型。当考虑边缘接触时,齿轮从进入到退出啮合需要建立46对模型,并以中间齿对为研究对象。中间齿对从开始接触到退出接触计为齿轮进入到退出啮合的过程。载荷较小时,中间齿对可能会出现不接触的现象,此时忽略计算结果,且对应数值取0。46对模型按照顺序连接起来,即可描述齿轮的整个啮合过程。

(a)无边缘接触

(b)有边缘接触图3 齿轮副传动误差曲线

条件设置如下。

(1)材料:大、小轮材料相同,弹性模量为206 GPa,泊松比为0.3,密度为7 800 kg/m3。

(2)接触对:根据大、小轮的接触面积建立接触对,根据七齿模型需建立7对接触面,接触属性为无摩擦硬接触。

(3)参考点:取轴线上一点为参考点,在参考点与大、小轮内圈和剖面间建立耦合关系,这样约束可以直接施加到参考点上。

(4)分析步:分析时采用静态分析方法,分析时间默认为1 s。

(5)输出变量:在场变量中输出变量,变量分别为参考点转角、接触应力、齿面点坐标等。

(6)边界条件及载荷:对小轮全约束,对大轮施加阻力矩且释放绕轴线的旋转自由度。

按上述条件编程生成inp文件,再利用批处理功能进行计算。本文通过施加不同的载荷来观察边缘接触的产生、发展以及对齿轮啮合性能参数的影响,载荷均为大轮负载,分别为50、500、1 500、2 500、3 500 N·m。

3 计算结果及分析

3.1 有限元计算结果及后处理

通过有限元计算,可以获得齿轮的应力分布云图。以大轮为例,进入啮合时分别截取了有边缘接触和无边缘接触时的应力云图分布,如图4所示。根据输出设置进行后处理,获得相关性能参数,具体方法参见文献[14]。

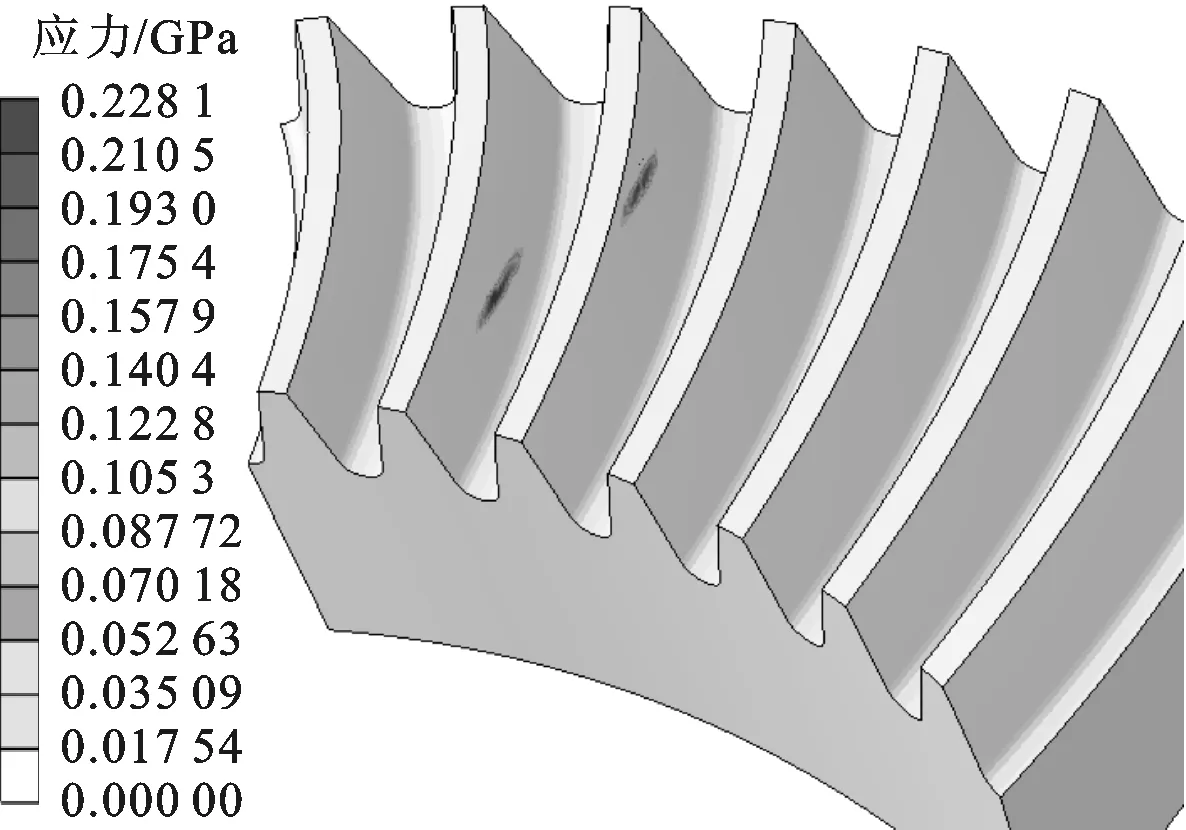
(a)无边缘接触

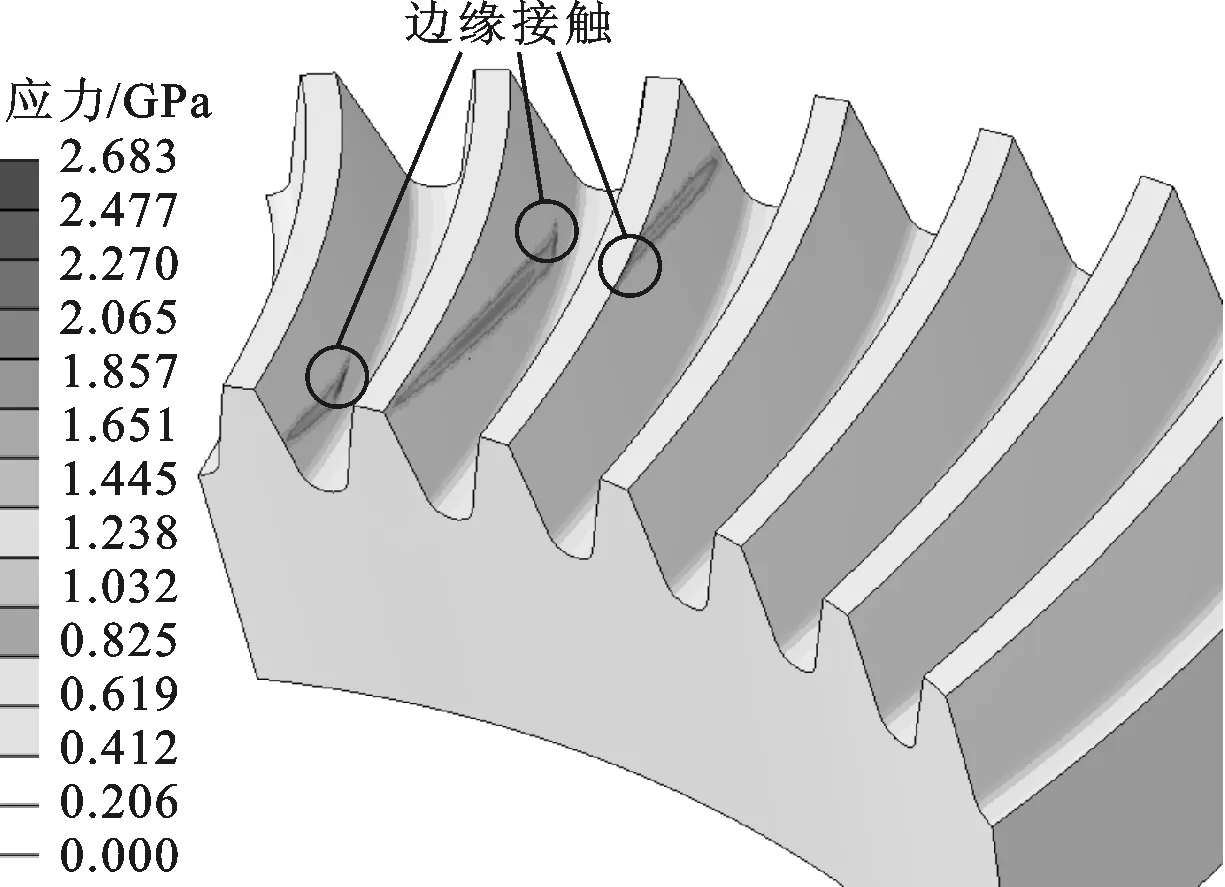
(b)有边缘接触图4 大轮应力分布云图

3.2 不同载荷条件下的接触应力

根据不同载荷条件下有限元分析的结果,分别绘制了接触应力曲线,如图5所示。

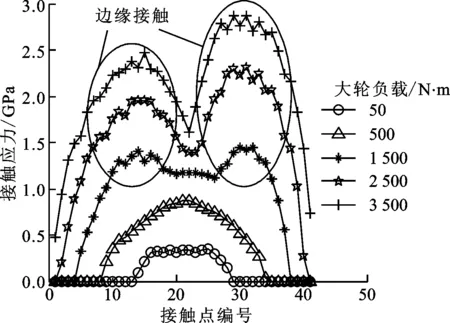
图5 不同载荷下的接触应力曲线

从图5可以看出,当载荷达到一定程度时,在进入啮合(大轮齿顶与小轮齿根啮合)和退出啮合(大轮齿根与小轮齿顶啮合)的位置均会出现明显的边缘接触现象,导致接触应力急剧上升,使得整个接触应力曲线呈凹状。从图5还可以看出,进入啮合时产生的边缘接触应力小于退出啮合时产生的边缘接触应力。

对于本算例来说,当载荷小于1 500 N·m时,没有边缘接触现象发生;当载荷达到1 500 N·m时,边缘接触开始出现。正常的接触应力约为1.185 GPa,边缘接触的应力峰值为1.439 GPa,约增大了20%。当载荷达到2 500 N·m时,边缘接触应力急剧增大,由正常接触应力时的1.385 GPa增大到2.226 GPa,约增加了60%。当载荷为3 500 N·m时,正常接触应力约为1.608 GPa,边缘接触产生的应力为2.754 GPa,约增加了71%。这说明载荷越大,边缘接触越明显,产生的边缘接触应力越大,边缘接触的位置数增多。

在有限元计算中,边缘接触导致了应力出现集中的现象,因此仿真计算得到的边缘接触应力往往比实际的要大。在实际加工中,边缘处倒棱,这会大大降低应力集中现象的产生。

3.3 不同载荷条件下的齿面接触印痕

根据接触应力大小以及齿面点坐标,可以近似绘制出不同载荷条件下的齿面印痕。利用Matlab的相关函数可以绘制出表示接触应力大小的云图,用以近似描述接触印痕;采用LTCA算法[2,13]可以计算齿面载荷的分布,用以表示接触区域,并与有限元计算结果进行对比,如图6所示。其中:有限元仿真印痕用云图形式表示,5个计算位置用同一个刻度来表示,印痕的分布用接触应力的大小来描述;LTCA用载荷分布图来表示。本文中以大轮齿面印痕为例进行讨论和分析。

从载荷变化云图来看,当载荷增大时,接触椭圆长轴变长,接触面积增大。当载荷达到3 500 N·m时,接触应力的分布几乎布满整个齿面。有限元与LTCA计算的印痕分布具有较高的一致性,不同之处在于:有限元计算采用应力作为衡量标准,发生边缘接触时最大应力产生在边缘处;LTCA以载荷为衡量标准,最大载荷在接触椭圆中心处。

(a)50 N·m有限元仿真

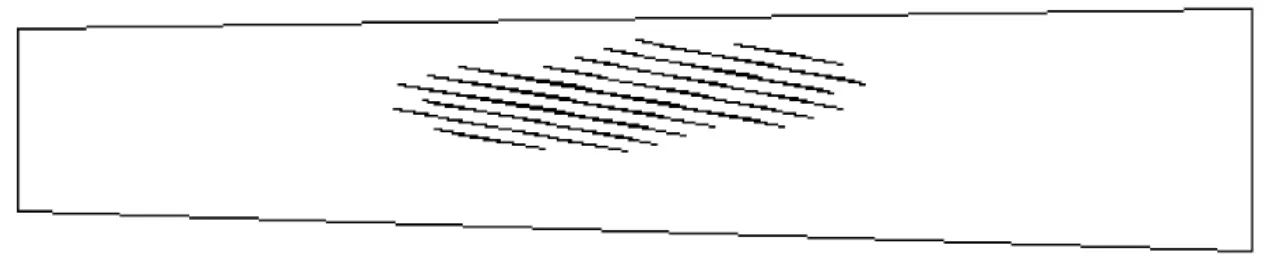
(b)50 N·m LTCA

(c)500 N·m有限元仿真

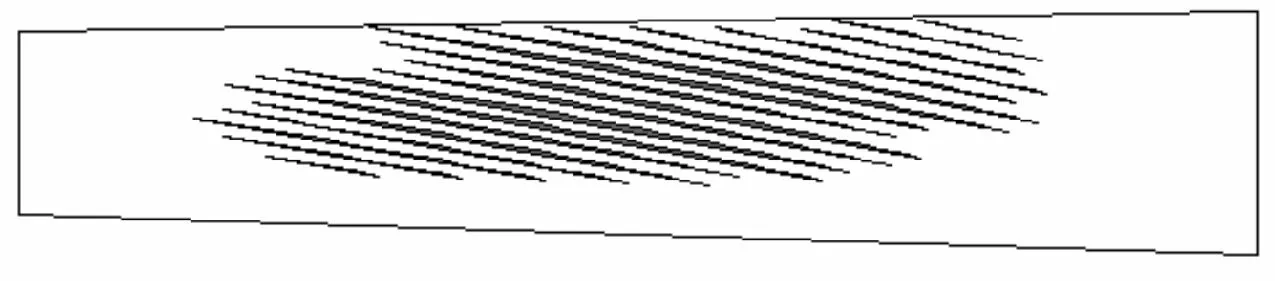
(d)500 N·m LTCA

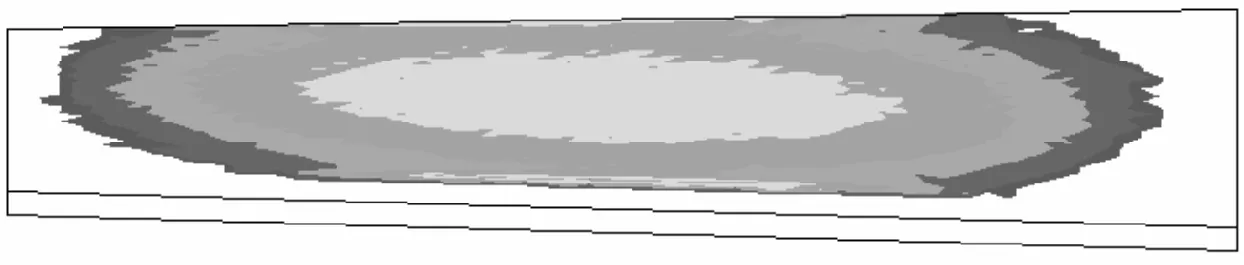
(e)1 500 N·m有限元仿真

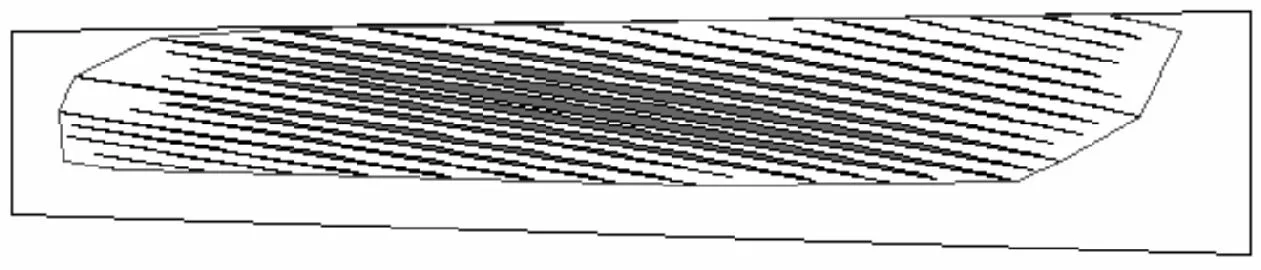
(f)1 500 N·m LTCA

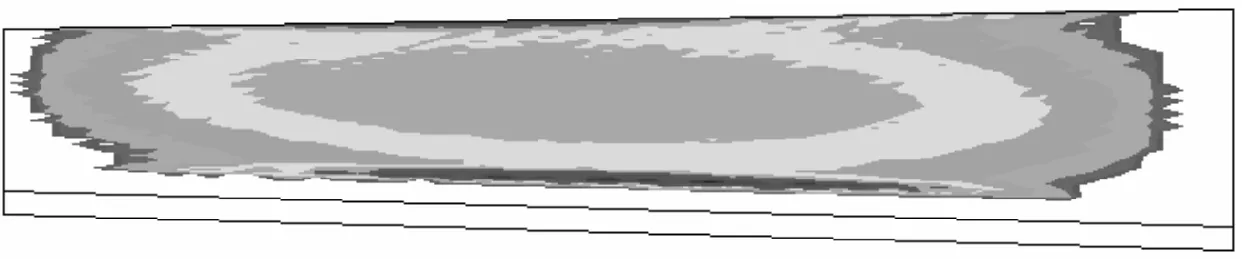
(g)2 500 N·m有限元仿真

(h)2 500 N·m LTCA

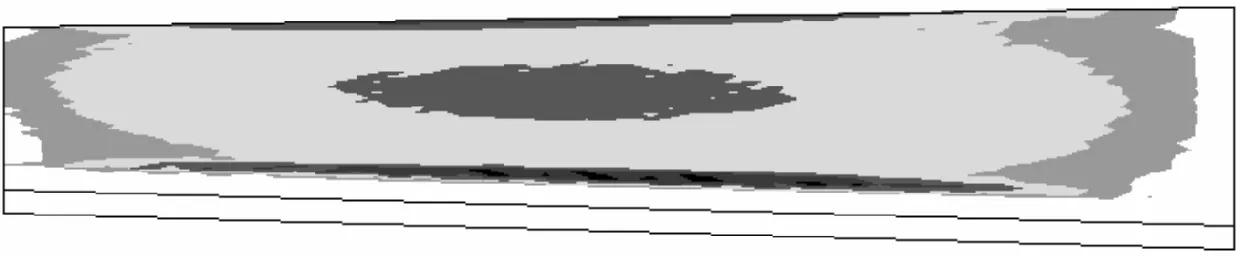
(i)3 500 N·m有限元仿真

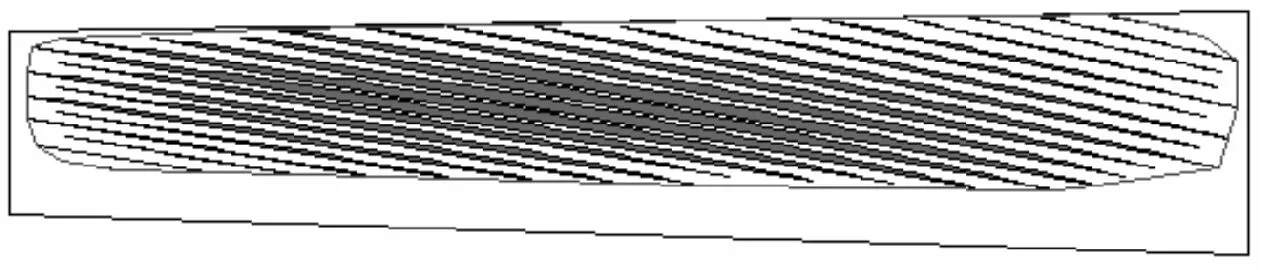
(j)3 500 N·m LTCA图6 不同载荷下的大轮齿面接触印痕

将齿轮印痕处的离散点拟合成最小凸多边形,可以近似求得印痕面积。5种载荷下求得的印痕面积依次为21.4、70.0、100.7、108.7、116.8 mm2,可以看出:载荷开始增加时,印痕发展较快,随着载荷的增大,印痕的变化率逐渐降低;当载荷增大至1 500 N·m时,齿顶和齿根处开始出现了边缘接触,即最大应力值不在印痕中心位置上;随着载荷的继续增大,边缘接触越来越明显,边缘上的应力值超过接触印痕中心位置处的应力值。大轮齿顶、齿根均发生边缘接触时,在大轮齿根处边缘接触应力较大,这与接触应力的计算结果是一致的。

3.4 不同载荷条件下的齿面接触路径

对齿轮进行TCA仿真时,只能确定接触路径的方向,不能判定接触路径的长短或者是否发生边缘接触。根据有限元计算结果,以中间齿对为研究对象,将中间齿对发生接触的位置计为有效,忽略未接触的位置,重新绘制TCA路径。同时,根据瞬时接触椭圆求解中心点位置,绘制出有限元计算结果所得的接触路径,如图7所示。文中算例为大轮齿面。

(a)50 N·m TCA

(b)50 N·m有限元仿真

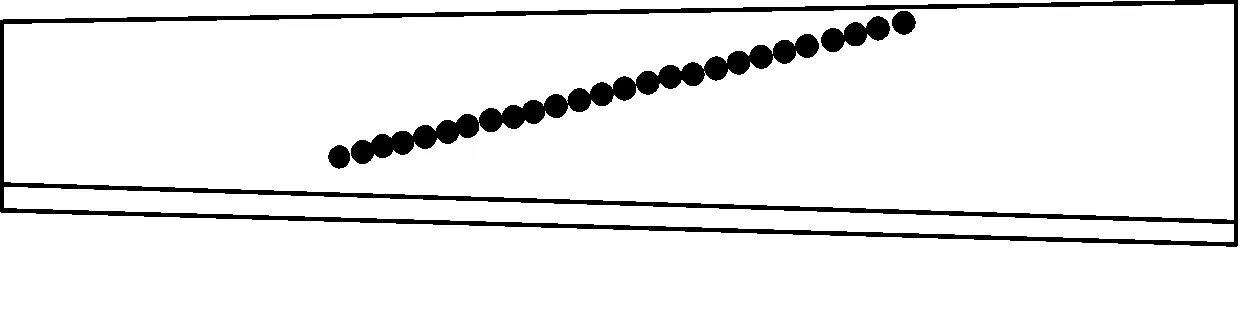
(c)500 N·m TCA

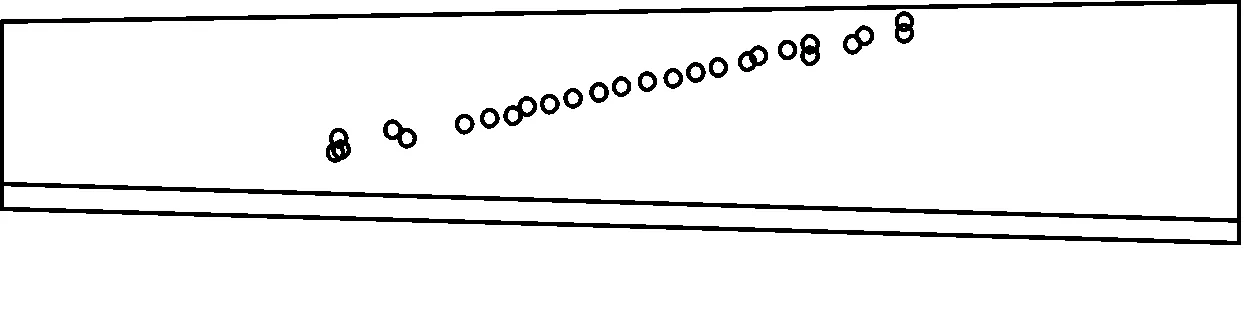
(d)500 N·m有限元仿真

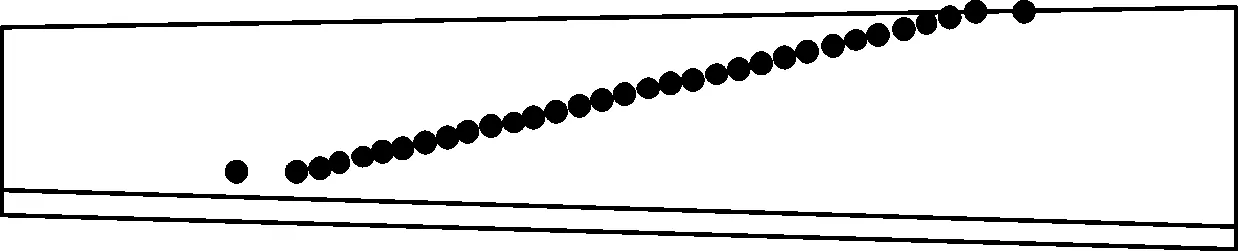
(e)1 500 N·m TCA

(f)1 500 N·m有限元仿真

(g)2 500 N·m TCA

(h)2 500 N·m有限元仿真

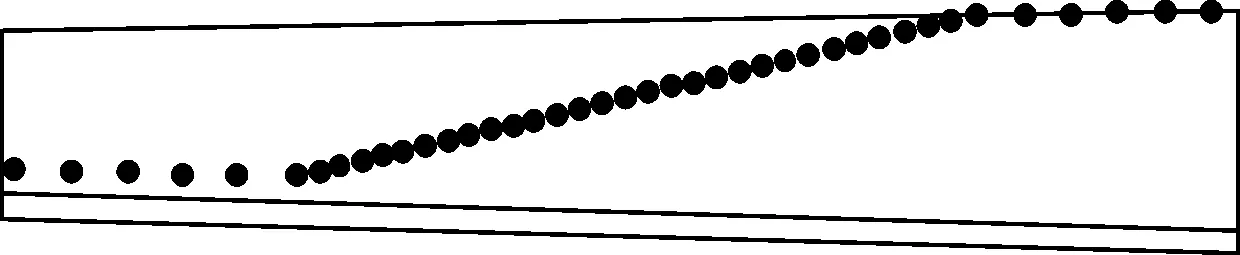
(i)3 500 N·m TCA

(j)3 500 N·m有限元仿真图7 不同载荷下的大轮齿面接触路径

从图7可以看出,有限元仿真结果所提取的接触路径与TCA结果基本一致,仅在发生边缘接触时有些差异。当载荷为1 500 N·m时,恰好发生边缘接触,且每种载荷条件下的接触路径长短及位置都有清晰的描述,表明有限元计算可以弥补TCA不能确定接触迹线的不足。

4 结 论

(1)根据啮合原理的基本理论以及有限元方法,编写了精确的有限元网格模型,根据TCA结果,将齿轮从进入啮合到退出啮合划分成多个位置,从而实现多个位置的批处理运行和后处理运算。每个位置均采用静态接触算法,串联不同装配位置的接触状态,得到齿轮从进入到退出啮合的变化过程。采用静态算法忽略了齿轮的惯性力因素,与LTCA等传统计算方法具有可比性,显示出静态模式计算速度快、计算效率高的优势。

(2)以一对弧齿锥齿轮为例,采用上述批处理方法对不同载荷条件下的啮合性能进行了定量分析,并与TCA、LTCA进行了对比。结果表明,载荷增大时会出现明显的边缘接触现象,接触路径增长,接触区域变大,齿轮退出啮合时边缘接触比进入啮合时明显。有限元计算与LTCA计算所得印痕吻合较好,有限元计算得到接触路径与TCA结果较一致,表明有限元计算可以较精确地确定使齿轮发生边缘接触现象时的载荷临界值及发生边缘接触的位置。

(3)根据有限元计算分析边缘接触的应力曲线结果可以看出,载荷增大且产生边缘接触时,接触应力会急剧增大,这是由于有限元计算中,边缘上的接触产生了应力集中现象。实际加工中,会在齿顶边缘处倒棱,从而避免应力集中现象,降低了边缘接触的应力。

本文以一对确定的弧齿锥齿轮为例进行计算分析,没有考虑加工参数对齿面的影响,未来进行齿轮边缘接触的相关工作应当考虑加工参数设计和齿面优化等内容。

[1] 高建平, 方宗德, 杨宏斌. 螺旋锥齿轮边缘接触分析 [J]. 航空动力学报, 1998, 13(3): 289-292. GAO Jianping, FANG Zongde, YANG Hongbin. Analysis of edge contact for hypoid gear and spiral bevel gears [J]. Journal of Aerospace Power, 1998, 13(3): 289-292.

[2] 方宗德, 邓效忠, 任东锋. 考虑边缘接触的弧齿锥齿轮承载接触分析 [J]. 机械工程学报, 2002, 38(9): 69-72. FANG Zongde, DENG Xiaozhong, REN Dongfeng. Loaded tooth contact analysis of spiral bevel gears considering edge contact [J]. Journal of Mechanical Engineering, 2002, 38(9): 69-72.

[3] RODA-CASANOVA V, SANCHEZ-MARIN F T, GONZALEZ-PEREZ I, et al. Determination of the ISO face load factor in spur gear drives by the finite element modeling of gears and shafts [J]. Mechanism and Machine Theory, 2013, 65: 1-13.

[4] WANG Pei-yu, FAN Sih-ci, HUANG Zi-gui. Spiral bevel gear dynamic contact and tooth impact analysis [J]. Journal of Mechanical Design, 2011, 133(8): 084501.

[5] WANG Huanmei, TANG Yingshi, GONG Yongliang. Accurately parameterization modeling and thermo-mechanical coupling analysis of spiral bevel gears of reducer [J]. Applied Mechanics and Materials, 2012, 184/185: 37-40.

[6] MERMOZ E, ASTOUL J, SARTOR M, et al. A new methodology to optimize spiral bevel gear topography [J]. CIRP Annals: Manufacturing Technology, 2013, 62(1): 119-122.

[7] 唐进元, 蒲太平. 基于有限元法的螺旋锥齿轮啮合刚度计算 [J]. 机械工程学报, 2011, 47(11): 23-29. TANG Jinyuan, PU Taiping. Spiral bevel gear meshing stiffness calculations based on the finite element method [J]. Journal of Mechanical Engineering, 2011, 47(11): 23-29.

[8] 唐进元, 彭方进. 准双曲面齿轮动态啮合性能的有限元分析研究 [J]. 振动与冲击, 2011, 30(7): 101-106. TANG Jinyuan, PENG Fangjin. Finite element analysis for dynamic meshing of a pair of hypoid gears [J]. Journal of Vibration and Shock, 2011, 30(7): 101-106.

[9] CHEN Y C, LO C C. Contact stress and transmission errors under load of a modified curvilinear gear set based on finite element analysis [J]. Proceedings of the Institution of Mechanical Engineers: Part C Journal of Mechanical Engineering Science, 2015, 229(2): 191-204.

[10]LITVIN F L, FUENTES A, HAYASAKA K. Design, manufacture, stress analysis, and experimental tests of low-noise high endurance spiral bevel gears [J]. Mechanism and Machine Theory, 2006, 41(1): 83-118.

[11]WU R Y. Analysis on contact stress after gear meshing and finite element of stiffness [J]. Applied Mechanics and Materials, 2015, 716: 670-675.

[12]FUENTES A, RUIZ-ORZAEZ R, GONZALEZ-PEREZ I. Computerized design, simulation of meshing, and finite element analysis of two types of geometry of curvilinear cylindrical gears [J]. Computer Methods in Applied Mechanics & Engineering, 2014, 272(2): 321-339.

[13]LITVIN F L, GONZALEZ-PEREZ I, FUENTES A, et al. Design, generation and stress analysis of face-gear drive with helical pinion [J]. Computer Methods in Applied Mechanics & Engineering, 2005, 194(36/37/38): 3870-3901.

[14]侯祥颖, 方宗德, 邓效忠, 等. 弧齿锥齿轮有限元建模与接触分析 [J]. 哈尔滨工程大学学报, 2015, 36(6): 826-830. HOU Xiangying, FANG Zongde, DENG Xiaozhong, et al. Contact analysis of spiral bevel gears based on finite element model [J]. Journal of Harbin Engineering University, 2015, 36(6): 826-830.

[15]方宗德. 齿轮轮齿承载接触分析(LTCA)的模型和方法 [J]. 机械传动, 1998, 22(2): 1-3. FANG Zongde. Model and approach for loaded tooth contact analysis (LTCA) of gear drives [J]. Journal of Mechanical Transmission, 1998, 22(2): 1-3.

[16]LITVIN F L, FUENTES A. Gear geometry and applied theory [M]. Cambridge, UK: Cambridge University Press, 2004: 627-676.

(编辑 苗凌)

Tooth Contact Analysis of Spiral Bevel Gears Considering Edge Contact with Finite Element Method

HOU Xiangying,FANG Zongde

(School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an 710072, China)

According to the lightweight and heavily loaded characteristics of spiral bevel gear, spiral bevel gears with tooth edge contact were analyzed by finite element processing batch, and the change regulation of tooth edge contact as load increases was quantitatively discussed. On the basis of tooth contact analysis, gear meshing processions were divided into several steps to calculate. Each step was combined to describe the gear meshing processions. Taking a pair of spiral bevel gears as an example, tooth edge contact is analyzed under different load conditions. The contact stress, contact pattern and contact trajectory were obtained by post-treatment, which well coincide with tooth contact analysis and loaded tooth contact analysis. The result shows that three tooth edge contact parameters listed above steeply rise as loads passing beyond the critical value. And the change characteristics can be obtained by quantitative calculation and parameter comparison.

spiral bevel gear; tooth edge contact; contact stress; contact pattern; finite element method

2016-04-05。 作者简介:侯祥颖(1990—),男,博士生;方宗德(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(51175423,51375384)。

时间:2016-09-08

10.7652/xjtuxb201611011

TH132.41

A

0253-987X(2016)11-0069-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160908.1103.004.html