水下滑翔机海底驻留流体动力及稳定性仿真

张宝收,宋保维,毛昭勇,姜军

(西北工业大学航海学院,710072,西安)



水下滑翔机海底驻留流体动力及稳定性仿真

张宝收,宋保维,毛昭勇,姜军

(西北工业大学航海学院,710072,西安)

为了研究水下滑翔机的稳定驻留问题进行了数值仿真,包括定义滑翔机的2种失稳状态,即流体对驻留平台的作用力大于支架与海底的摩擦阻力时发生的滑移,以及流体对驻留平台的翻转力矩大于负浮力所能提供的最大约束力矩时发生的翻转,建立临界失稳的数学模型。考虑滑翔机与流场和海床的复合影响,运用Ansys CFX软件完成了数值仿真,仿真时研究了流场速度0～2 m/s、浮心到海底距离0.15～0.5 m以及不同攻角及方位角对驻留状态的影响,由此绘制了流体对驻留平台的作用力和力矩变化曲线。研究结果表明:浮心到海底距离小于0.3 m时壁面效应明显,有利于稳定驻留;滑翔机驻留攻角将极大影响驻留平台的稳定性;方位角在150°～155°时流体扰动最大。该结果可为滑翔机的设计定型和实际驻留研究提供参考。

水下滑翔机;稳定驻留;数值仿真

水下滑翔机(Glider)是一种新型无人水下航行器,其利用质心和浮力调节机构产生滑翔驱动力,相比细长回转体型航行器,续航时间长、稳定性高。此滑翔机具有翼身融合外观,能更好地利用流体升力,实现大滑翔比运动[1]。

当航行器需要定点探测某一固定海域或定点潜伏时,需要具有稳定的驻留能力。目前,针对各种新型水下航行器驻留平台的研究已成为国内外的热点。对于锚泊型驻留平台,田文龙等进行了缆绳系泊发电的仿真研究[2]。Johanning等通过对链条离散化建模得到了外力干扰下链条的数学模型[3-4]。Mavrakos等完成了理想链条深水动力学建模[5]。水下航行器的锚泊驻留方式结构简单,但对于需要保持稳定姿态的航行器,此种驻留方式约束不足。

王晓鸣等系统研究了自主式水下航行器(AUV)水下着陆策略,确定了坐底着陆的可行性[6]。Smallwood等对航行器的驻留运动过程进行了数学建模[7]。朱信尧等对坐底型水下航行器的流体动力特性和稳定性进行了仿真研究[8]。宋保维等对无人水下航行器(UUV)海底驻留运动和关键技术进行了仿真和实验[9-10]。坐底型水下航行器需要附着物较少的平坦海底。

本文提出了翼身融合型水下滑翔机(简称水下滑翔机)的液压驻留方式,如图1所示,其采用液压支架(LG)支撑在海床上,在保持滑翔机自身稳定的基础上远离海底因素的干扰,保证更好地完成定点潜伏探测、侦查反蛙人等相关任务。此驻留方式受力特性和稳定性的相关研究,可为后续实验设计等提供有意义的参考。

图1 水下滑翔机海底驻留

1 驻留状态的数学模型

1.1 驻留失稳的定义

水下滑翔机驻留平台的稳定性是指受到流体扰动后,不发生位置和姿态的变化。驻留平台失稳形式主要有两种:流体对驻留平台的作用力大于液压支架与海底的水平摩擦阻力时发生的滑移,如图2a所示;流体对驻留平台的翻转力矩大于负浮力所能提供的最大约束力矩时发生的翻转,如图2b所示。

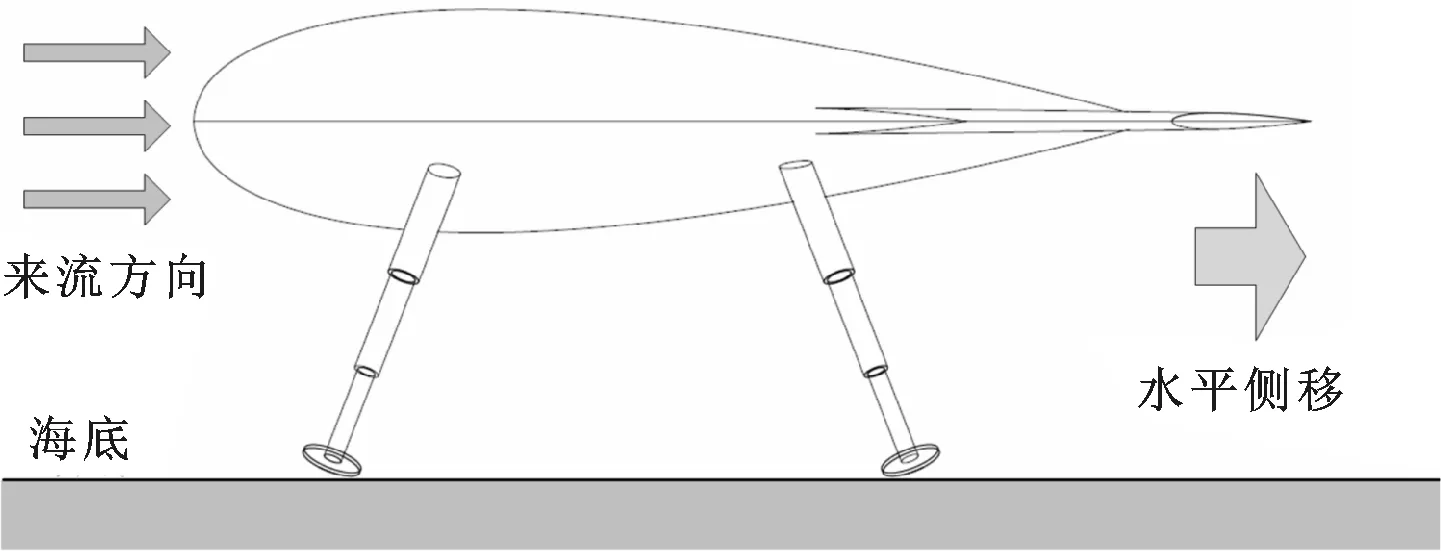
(a)滑移

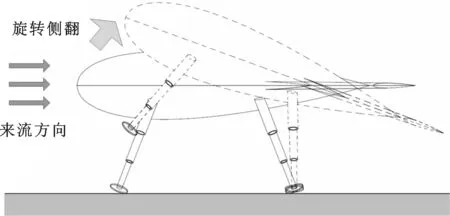
(b)翻转图2 水下滑翔机驻留时两种失稳形式

1.2 驻留失稳的数学建模

针对水下滑翔机驻留平台失稳的两种形式,分析了其受力特性。下面就两种失稳分别建立临界状态的平衡方程。

(1)滑移。液压支架与海底摩擦系数为k0,驻留平台重力为G、浮力为N,临界失稳状态的数学模型为

Fx+FLx-k0(ΔG-Fy-FLy)≥0

(1)

式中:Fx为流体对滑翔机水平方向的作用力;Fy为流体对滑翔机垂直方向的作用力;FLx为流体对液压支架水平方向的作用力;FLy为流体对液压支架垂直方向的作用力;ΔG为驻留平台受到的负浮力。

根据仿真实验,作用力系数Cx[11]是关于攻角变化的经验参考值,即Cx=0.003 09α2-0.002 19α+0.114 46,由下式确定

Fx=∫Ωt[-pcos(n,x)+τcos(t,x)]dΩt=

(2)

ΔG=G-N

(3)

式中:S为特征面积,即滑翔机在运动方向的投影面积;v∞为来流速度。

(2)翻转。当驻留平台相对于后支点PB受到的流体力矩超过负浮力对PB点的力矩时发生侧翻,此时的临界状态为前支点PA受到的海底支撑力为0。该临界失稳的数学模型为

(Fy+FLy-ΔG)L1≥0

(4)

式中:FP为在前端支点PA处受到的海底支撑力;M0为UUV对支点PB的流体力矩;ML为液压支架对支点PB的流体力矩,通过仿真可直接获得。

前、后俯仰侧翻如图3a所示,若来流方向为侧向,则翻转绕侧面支点进行,如图3b所示。

(a)侧视图

(b)正视图图3 水下滑翔机驻留受力特性

2 数值计算方法

2.1 流体计算控制方程

对流动问题的求解即是对纳维-斯托克斯(N-S)方程的求解[12]。不可压缩流动控制方程为连续方程和N-S方程

·U=0

(5)

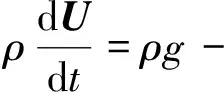
(6)

式中:U为速度矢量;μ为流体动力黏性系数。

2.2 边界条件

通过建立流场边界构成计算域,这样将外部绕流问题转变为内流问题。驻留平台流场的计算域如图4所示,其边界条件设定如下。

(1)入口:选用Inlet边界类型,速度方向与壁面垂直,湍流强度根据流速变化确定。

(2)出口:选用Outlet边界类型,出口压力为0 Pa。

(3)上壁面和左右壁面:设定为自由滑移壁面。

(4)下壁面:考虑近壁面效应,选用无滑移壁面。

(5)液压支架和滑翔机:无滑移壁面。

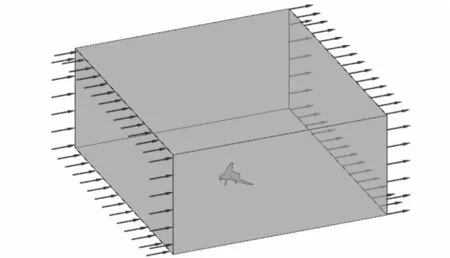
图4 流场计算域

本文假设不考虑流体对UUV和支架的作用力产生形变的影响,挡泥板与泥沙(计算域的下壁面)为刚性接触。

3 数值仿真计算

3.1 三维模型与网格划分

滑翔机整体为扁平三角形,纵平面和水平面对称[1],主要参数如表1所示。为保持滑翔机较高的灵活性,设计时不会存有较大的剩余浮力。滑翔机驻留采取4根关于中心对称布置的斜置3级液压支架,并通过挡泥板与海底接触,摩擦系数k0来自实验数据,约为0.8,即为正常无沉降条件下液压杆(钢材)与泥沙发生相对滑动时的最大摩擦系数。

表1 水下滑翔机主要参数

水下滑翔机驻留平台的外形结构复杂,为保证网格更好地贴合滑翔机表面,本文采用加密细化的非结构网格,并以Ansys ICEM软件为工具进行网格划分[13],结果如图5所示。

(a)流场整体网格 (b)滑翔机头部网格图5 驻留状态整体网格及局部表面细节网格

3.2 驻留状态的计算工况

本文数值模拟了流场速度v、滑翔机浮心到海底的距离H、滑翔机攻角α和驻留方位角φ的工作状况,如表2所示。

表2 驻留状态的计算工况

3.3 求解结果

对速度为1 m/s、浮心到海底距离为0.4 m、攻角为0°的数值仿真结果经后处理,得到的压力分布云图、流线图如图6、图7所示。可以看出,在滑翔机迎流前端和液压支架迎流面均出现了一条高压带。

图6 滑翔机表面压力分布云图

图7 滑翔机表面流线发展图

驻留平台纵平面内的压力分布云图和流线图如图8、图9所示。可以看出:滑翔机前端流场出现高压区域,流速减小,流场未出现明显分离;滑翔机后端压力明显小于前端,前后压差产生了流体阻力。

图8 纵平面内压力云图

图9 纵平面内流线图

驻留平台侧平面内压力分布云图和流线图如图10、图11所示。可以看到,滑翔机正前端出现低速高压流场,与纵平面内流场相似。

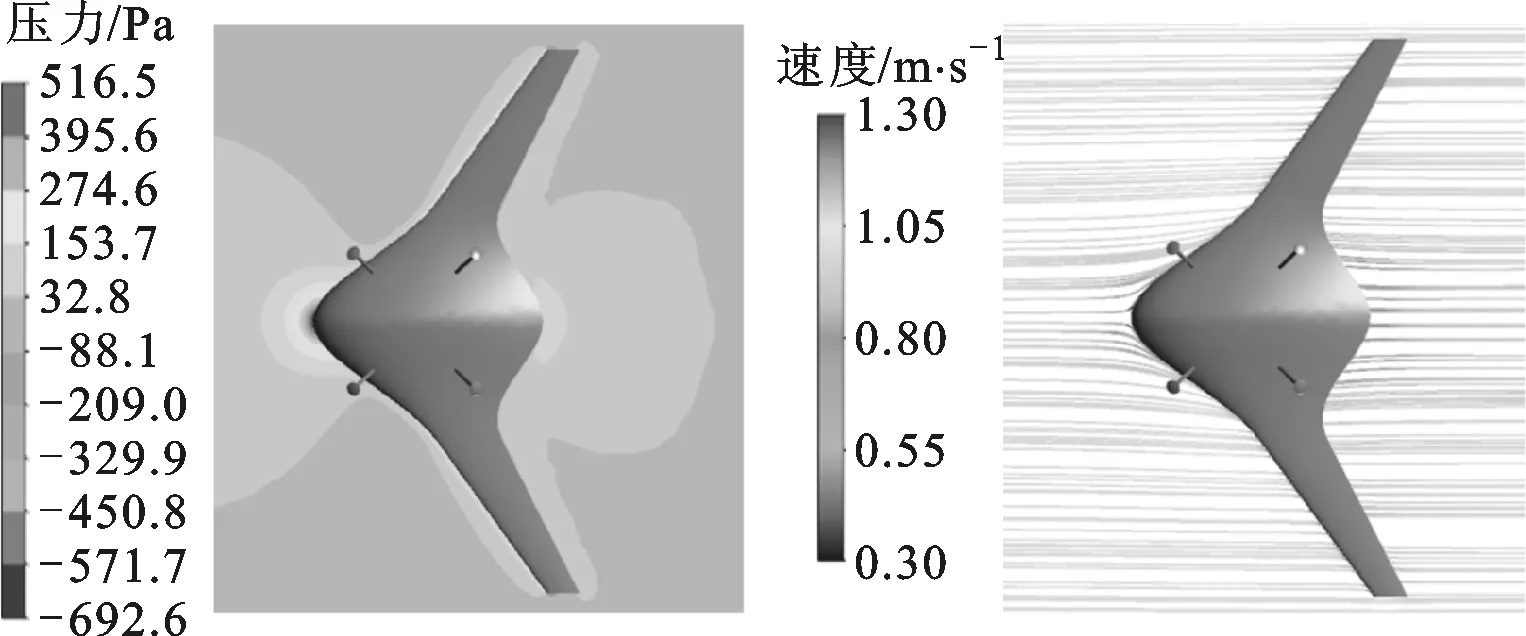
图10 侧平面内压力云图 图11 侧平面内流线图

4 结果处理与分析

4.1 流速对驻留的影响

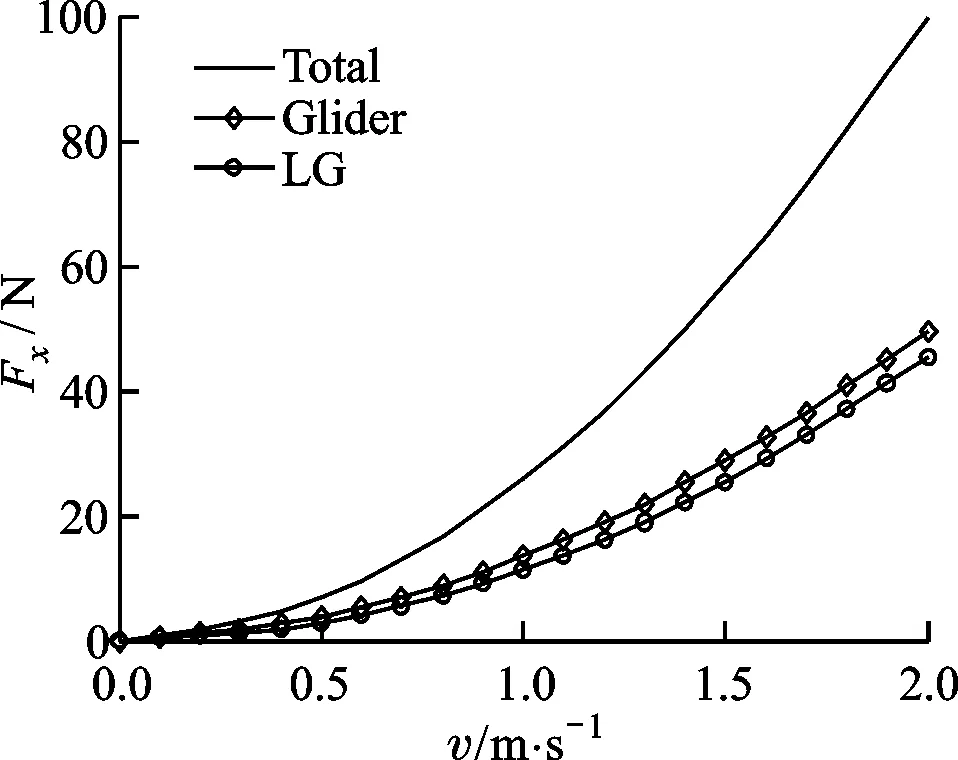
(a)Fx与速度的关系

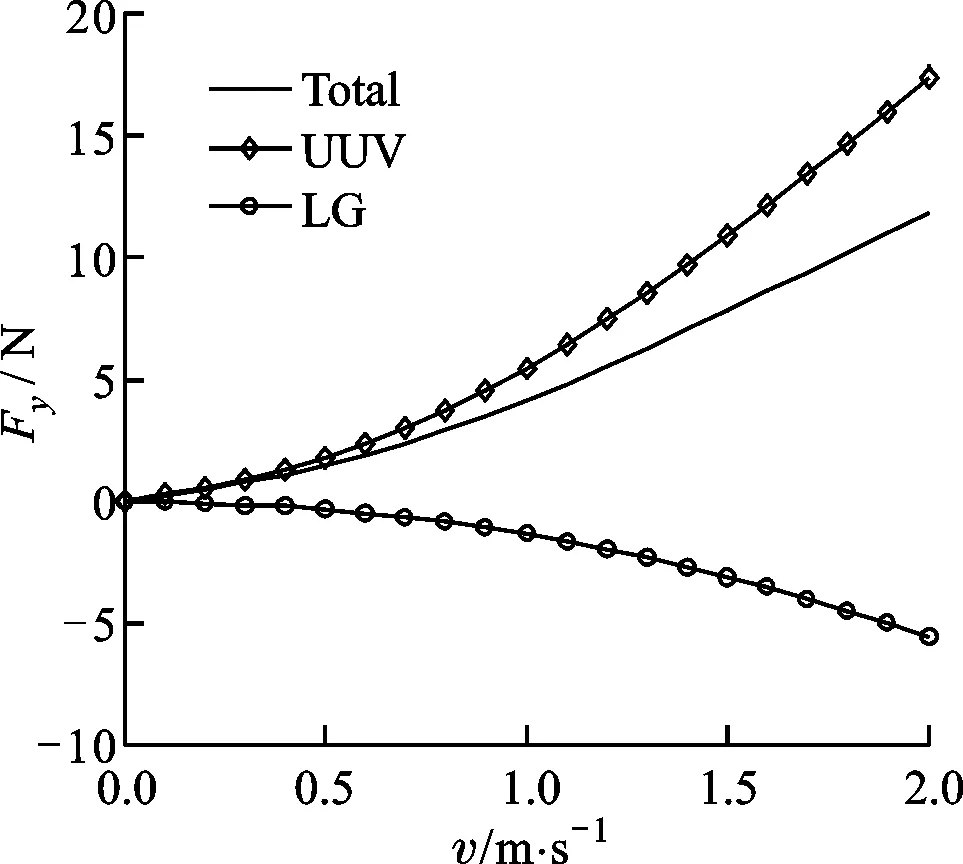
(b)Fy与速度的关系图12 流体对驻留平台的作用力与速度的变化关系

图13 流体对驻留平台的力矩与速度的变化关系

在平坦海底条件下,选定滑翔机浮心到海底距离为0.3 m,由此分析流速对驻留状态的影响。流体作用力和力矩随速度的变化如图12、图13所示。可以看出:Fx和Fy随流速的增大而增大;FLx和FLy随流速的增大而增大。显然,流体对驻留系统整体(Total)的作用力和力矩均随速度的增大而增大。竖直方向流体作用力的增大,会导致驻留系统对海底的压力减小,从而摩擦力减小。

为防止滑移失稳,需要调整负浮力,在最大速度条件下,根据式(1)得ΔG不小于137 N。为防止翻转失稳,根据式(4)得ΔG不小于98.5 N。可见,滑移失稳相比翻转更容易发生。

4.2 到海底壁面的距离对驻留的影响

(a)Fx

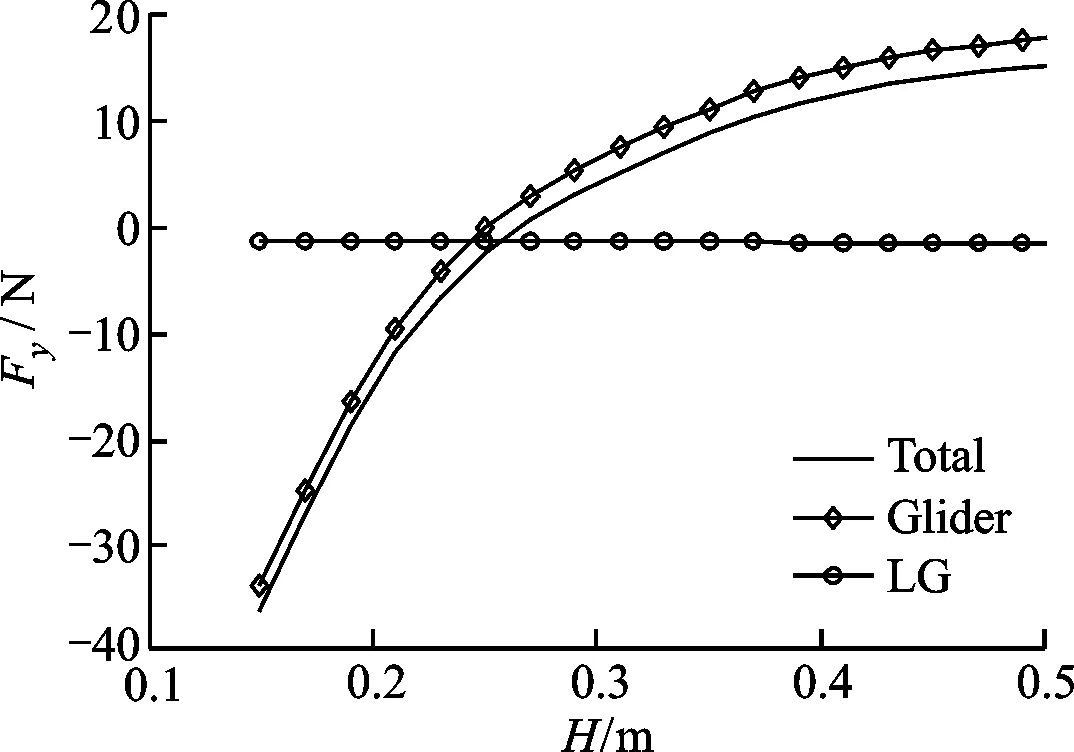
(b)Fy图14 流体对驻留平台的作用力与到海底距离的变化关系

图15 流体对驻留平台的力矩与到海底距离的变化关系

取流场v=1 m/s来分析滑翔机无攻角迎流时浮心到海底距离对驻留的影响。力和力矩随浮心到海底距离变化的拟合曲线如图14、图15所示。可以看出,随着浮心距离的增大,支架伸出的长度增加,流体作用力和力矩增大。离海底壁面越近,近壁面效应越大,滑翔机与海底壁面之间的流速越大、压强减小。流体对滑翔机竖直向下的作用力增大,将驻留平台压向海底。当离海底壁面距离超过0.3 m时,壁面效应减小,受海底壁面干扰流体存在向上的速度,滑翔机受到的升力较小。随着浮心到海底距离的增大,支点的力矩增大,驻留系统越容易倾覆。

为保持滑翔机稳定,不发生滑移,根据式(1)得ΔG不小于60.75 N。为保证不发生翻转失稳,根据式(4)得ΔG不小于47.48 N。

4.3 滑翔机攻角对驻留的影响

下面分析滑翔机攻角在-12°～+12°范围内对驻留的影响。力和力矩随攻角变化的拟合曲线如图16、图17所示。可以看出,随着攻角的增大,滑翔机受到的阻力先减小再增大,且关于零攻角对称。分析升力从-415 N增大到315 N,力矩从-81 N·m增大到69 N·m可知,当升力和力矩为负值时,滑翔机压紧在海床上。水下滑翔机驻留在不平坦的海床时受到的外力扰动较大,需要提供较大的负浮力,以克制失稳发生。

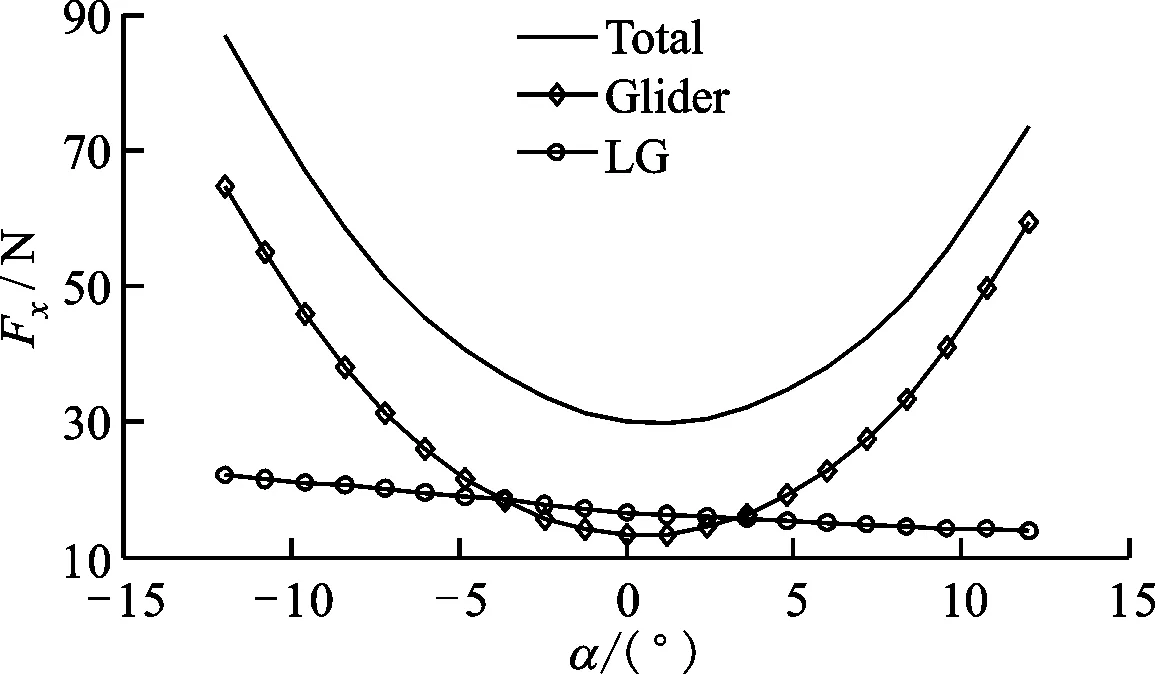
(a)Fx

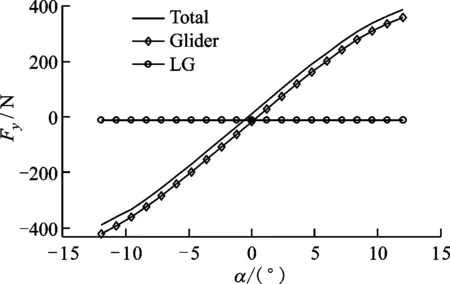
(b)Fy图16 流体对驻留平台的作用力与攻角的变化关系

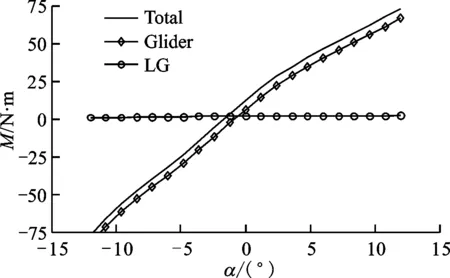
图17 流体对驻留平台的力矩与攻角的变化关系

根据式(1),在攻角为+12°时最易发生滑移,为保证不发生滑移,最小负浮力ΔG应不小于451 N。根据式(4),在攻角为+12°时最易发生翻转,为不产生失稳,最小负浮力ΔG应不小于546 N。

4.4 滑翔机驻留方位角对驻留的影响

滑翔机驻留时,其头部难以保证正向迎流,会与洋流存在夹角,其定义为方位角φ,如图18所示。

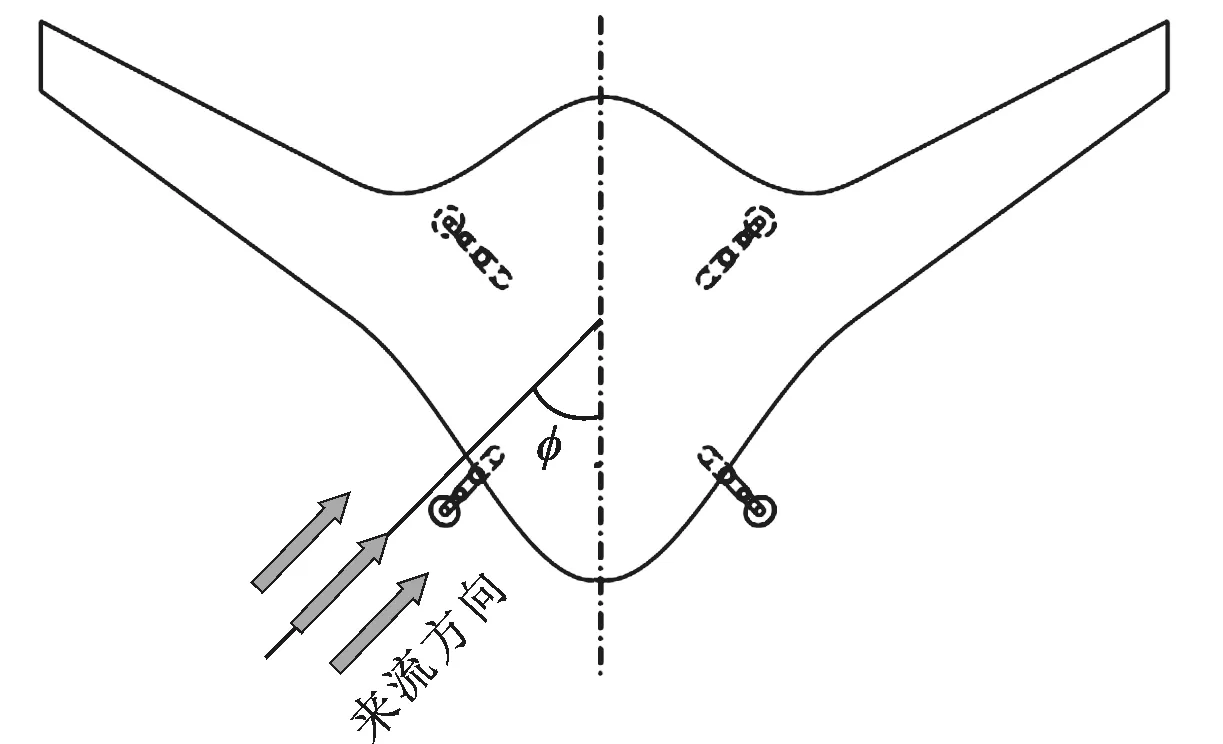
图18 滑翔机驻留方位角示意图

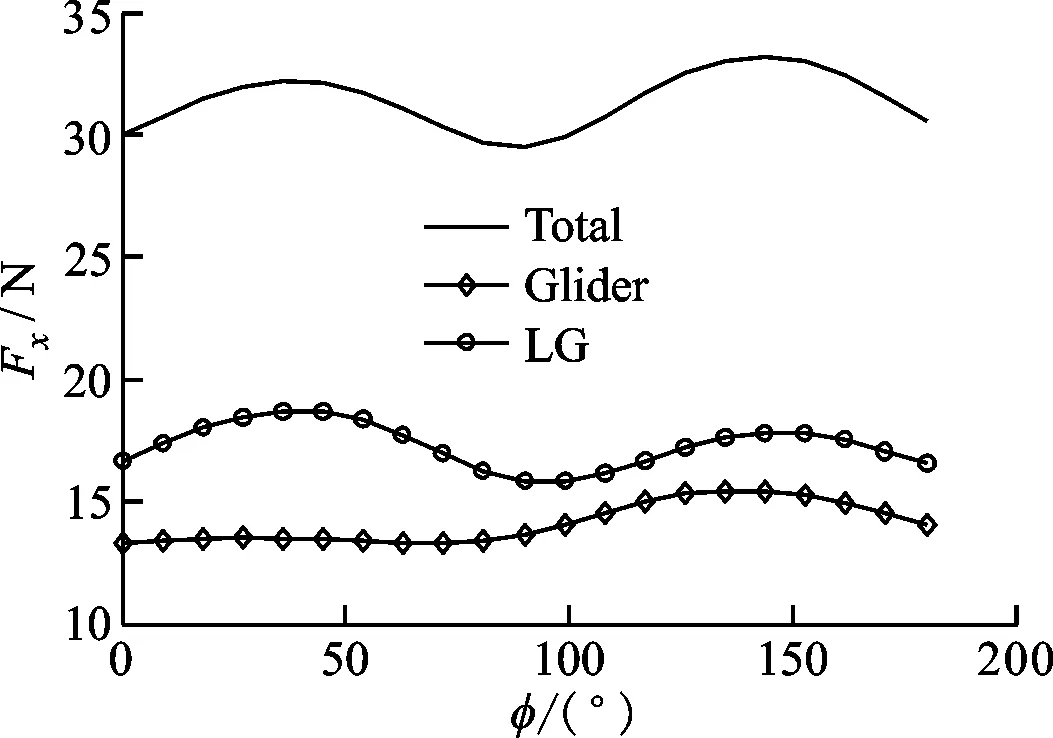
(a)Fx

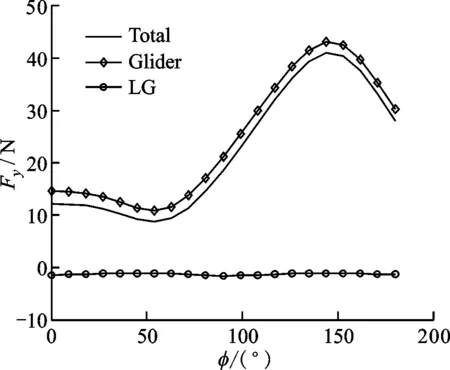
(b)Fy图19 流体对驻留平台的作用力与方位角的变化关系

在平坦海底,浮心到海底距离为0.4 m,方位角从0°增加到180°时,滑翔机的迎流截面发生复杂变化,其受力和力矩曲线变化规律复杂,如图19、图20所示。方位角在30°和150°附近,阻力最大,在150°附近升力最大。同时,因滑翔机外形在流场速度方向左右不对称,所以水平面内有相互垂直的两个作用力,其产生的力矩可被分解为使滑翔机前后俯仰翻转和左右侧翻转的两个力矩,较大的力矩易导致侧翻。可以看出,在155°附近出现了最大力矩。

图20 流体对驻留平台的力矩与方位角的变化关系

方位角为150°～155°时,为保持滑翔机稳定,不发生滑移,根据式(1)得ΔG不小于约81.4 N。

式(4)中M0和ML是关于方位角φ的函数,应根据方位角φ修正选取。当φ在0°～37°和135°～180°范围内发生前后俯仰翻转时,M0和ML应按虚线数据选取;当φ在37°～135°内发生左右侧翻时,M0和ML应按实线数据选取。可见,为保证不发生翻转失稳,根据式(4)得ΔG不小于81.8 N。

综合分析可知,方位角在150°～155°的范围内,驻留稳定性最差,实际应用时应加以考虑。

5 结 论

本文对水下滑翔机的海底定点驻留进行了数值仿真研究,推导了平台失稳状态的数学模型,完成了驻留状态受力和力矩特性的研究,分析了不同工况条件下受力特性和稳定性,由此得到如下结论。

(1)洋流流速对滑翔机稳定驻留影响较大,流体对驻留系统的作用力和力矩与速度的平方成正比。

(2)驻留平台受到壁面效应的影响,离海底越近,流体对滑翔机竖直方向的作用力越大,有利于将滑翔机压紧在海床上。但是,离海底距离过近会受海底泥沙、植被等影响,不利于起锚航行。当距海底超过0.3 m时,壁面效应的影响减小。

(3)当海底不平坦、驻留平台出现攻角时,流体对驻留系统的作用力和力矩均以较快速度增大,实际驻留时应当避免崎岖复杂的海底地形。驻留时存在方位角,迎流状况不同,在150°～155°范围内流体扰动最大,所以实际驻留时应避免此迎流角度。

本文研究可为水下滑翔机实现稳定驻留提供一种可供参考的数值模拟方法和理论依据,为开展水下滑翔机的驻留实验等提供有意义的参考。

[1] SUN Chunya, SONG Baowei, WANG Peng. Parametric geometric model and shape optimization of an underwater glider with blended-wing-body [J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7: 995-1006.

[2] 田文龙, 宋保维, 毛昭勇, 等. 水下航行器垂直轴海流发电装置叶轮特性的数值仿真 [J]. 西安交通大学学报, 2013, 11(47): 19-24. TIAN Wenglong, SONG Baowei, MAO Zhaoyong, et al. Numerical analysis on impeller behavior of vertical axis water turbine for underwater vehicles [J]. Journal of Xi’an Jiaotong University, 2013, 47(11): 19-24.

[3] JOHANNING L, SMITH G H, WOLFRAMC J. Measurement of static and dynamic mooring line damping and their importance for floating WEC devices [J]. Ocean Engineering, 2007, 34: 1918-1934.

[4] WANG Lizhong, GUO Zhen, YUAN Feng. Three-dimensional interaction between anchor chain and seabed [J]. Applied Ocean Research, 2010, 32: 404-413.

[5] MAVRAKOS S A, PAPAZOGLOU V J, TRIANTAFYLLOU M S. Deep water mooring dynamics [J]. Marine Structures, 1996, 9: 181-209.

[6] 王晓鸣, 王树新, 张宏伟. AUV水下着陆策略研究 [J]. 机器人, 2008, 30(4): 346-352. WANG Xiaoming, WANG Shuxin, ZHANG Hongwei. Research on the underwater landing strategy of AUV [J]. Robot, 2008, 30(4): 346-352.

[7] SMALLWOOD D A, WHITCOMB L L. Model-based dynamic positioning of underwater robotic vehicles: theory and experiment [J]. IEEE Journal of Oceanic Engineering, 2004, 29(1): 169-186.

[8] 朱信尧, 宋保维, 单志雄, 等. 海底定点停驻无人水下航行器流体动力特性分析 [J]. 上海交通大学学报(自然科学版), 2012, 46(4): 573-578. ZHU Xinyao, SONG Baowei, SHAN Zhixiong, et al.

Hydrodynamic characteristics analysis of UUV parking on the seabed [J]. Journal of Shanghai Jiaotong University (Natural Science Edition), 2012, 46(4): 573-578.

[9] 宋保维, 朱信尧, 曹永辉, 等. UUV海底停驻策略及其关键技术 [J]. 鱼雷技术, 2010, 18(6): 401-405. SONG Baowei, ZHU Xinyao, CAO Yonghui, et al. Strategy and key technologies of UUV parking on the seabed [J]. Torpedo Technology, 2010, 18(6): 401-405.

[10]YUH J. Design and control of autonomous underwater robots: a survey [J]. Autonomous Robots, 2000, 8(1): 7-24

[11]潘光. 鱼雷力学 [M]. 西安: 陕西师范大学出版社, 2013: 95-125.

[12]TIAN Wenlong, SONG Baowei, MAO Zhaoyong. Conceptual design and numerical simulations of a vertical axis water turbine used for underwater mooring platforms [J]. International Journal of Naval Architecture and Ocean Engineering, 2013, 5: 625-634.

[13]王海龙, 王刚, 陈曦, 等. 仿海蟹机器人游泳足水动力学分析与实验研究 [J]. 西安交通大学学报, 2015, 49(8): 75-83. WANG Hailong, WANG Gang, CHEN Xi, et al. Hydrodynamic analysis and experimental research on swimming leg of crablike robot [J]. Journal of Xi’an Jiaotong University, 2015, 49(8): 75-83.

[本刊相关文献链接]

王科燕,邓飞,张衡,等.超空泡航行器扩张尾裙流体动力特性试验研究.2016,50(1):53-58.[doi:10.7652/xjtuxb201601 009]

丁文俊,宋保维,毛昭勇,等.海洋动能发电装置在水下探测航行器的安装位置对发电性能的影响.2016,50(1):108-114.[doi:10.7652/xjtuxb201601017]

丁文俊,宋保维,毛昭勇,等.浅水域探测型无人水下航行器海洋动能发电装置特性研究.2014,48(4):73-78.[doi:10.7652/xjtuxb201404013]

田文龙,宋保维,毛昭勇,等.水下航行器垂直轴海流发电装置叶轮特性的数值仿真.2013,47(11):19-24.[doi:10.7652/xjtuxb201311004]

(编辑 苗凌)

Stability Simulation for Underwater Glider Parking on Seabed

ZHANG Baoshou,SONG Baowei,MAO Zhaoyong,JIANG Jun

(School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China)

To investigate the stability parking of an underwater glider, a numerical simulation is carried out. Two types of instability states of the underwater glider are defined, namely, “when the fluid drag exceeds the friction between the hydraulic support and the seabed, sideslip occurs” and “when the fluid torque relatively to the fulcrum exceeds the restoring torque from net gravity, side roll occurs”. The mathematical models of the instability state are established. Considering the coupling of the underwater glider between flow field and seabed, the numerical simulation is carried out with ANSYS-CFX. Under the conditions of different flow velocities (0-2 m/s), distances (0.15-0.5 m) and attitude angles, the curves of the fluid force and torque are completed. It reveals that when the distance between the buoyant and seabed is smaller than 0.3 m, wall effect is obvious, which is helpful in the stability of the glider, and attack angle of the glider greatly reduces the stability of the whole system; when azimuth angle is at 150°-155°, the disturbance of fluid is most obvious. The results can be used for practical design and parking experiment for a new underwater glider.

underwater glider; stability parking; numerical simulation

2016-03-10。 作者简介:张宝收(1991—),男,博士生;宋保维(通信作者),男,教授。 基金项目:国家自然科学基金资助项目(51179159)。

时间:2016-09-08

10.7652/xjtuxb201611008

TP242.3

A

0253-987X(2016)11-0049-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160908.1104.010.html