冲击特征受控极小化通用稀疏表示及其在机械故障诊断中的应用

贺王鹏,訾艳阳,陈彬强

(1.西安交通大学机械制造系统工程国家重点实验室, 710049, 西安;2.美国纽约大学 工程学院, 11201, 美国纽约;3.厦门大学航空航天学院, 361005, 福建厦门)



冲击特征受控极小化通用稀疏表示及其在机械故障诊断中的应用

贺王鹏1,2,訾艳阳1,陈彬强3

(1.西安交通大学机械制造系统工程国家重点实验室, 710049, 西安;2.美国纽约大学 工程学院, 11201, 美国纽约;3.厦门大学航空航天学院, 361005, 福建厦门)

针对强背景噪声下机械故障微弱暂态特征表示和有效提取的难题,提出了通用的稀疏优化特征提取算法。算法针对含噪声冲击性特征提取问题设计了稀疏优化表征函数,该函数融合了冲击特征的保真度与惩罚函数因子,考虑了正则化参数以适应不同工程背景下各分析因子的实际影响,实现处理结果稀疏性极大化。同时,引入受控极小化方法对设计的表征函数进行转化,分解成一系列凸优化分析问题。提出了针对离散信号的有限差分式数值迭代算法,验证了其快速收敛性和数值稳定性,提出的算法对机械故障诊断的数字采样信号具有普遍适用性。将所提出的算法应用于实验室环境下的轴承故障特征识别中,无论是低噪声还是低信噪比白噪声环境下,振动信号中的冲击特征都得到了显著增强,在Hilbert包络谱中的故障特征频率及其高次谐波比能量中占优。所提出的算法还应用于电力机车走行部轮对的故障诊断中,在高强度的工程有色噪声环境下精确提取了其中的冲击衰减成分,在时域和频域诊断结果中都得到了准确的验证,指导了诊断实践。

稀疏表示;凸优化问题;受控极小化;特征提取;故障诊断

我国正在大力发展高端装备制造产业,高端装备的核心价值主要体现在其运行过程。各行业中的许多重大关键机械设备长期运行在重载、腐蚀、高温等复杂恶劣的工况下,核心零部件将不可避免地发生各种程度的机械故障。信号处理和特征提取技术是机械设备状态监测和故障诊断的核心技术。部件故障的早期微弱故障特征提取的一个重要障碍是强背景噪声。

稀疏表示是近年来信号处理领域的热点之一[1],对特定信号进行稀疏表示的意义就是在给定的超完备字典中用尽可能少的原子来表示该信号,获得信号更为简洁的表示方式,以便更容易获取隐藏在信号中的有用信息[2]。工程中广泛应用的小波变换是基于内积原理的特征波形基函数信号分解,与故障特征最相似或局部最相似的小波基函数可以最佳地稀疏表征隐藏在混合信号中的故障信息[3-4],从时频分布特性的差别来说,小波变换可分为Mallat分形、Selesnick分形和Zi分形等种类[5]。目前的降噪方法往往针对信号中的高阶可导趋势项、分段光滑趋势项,以及冲击性信号出现时间的时刻特征进行了较好的处理,而在强噪声背景下较完整地提取出能量微弱的振荡衰减冲击性特征依然具有很大的挑战。

本文针对强背景噪声中微弱故障特征提取的难题,构造了新的稀疏优化目标函数,并且引入受控极小化(MM)方法进行推导求解。利用受控极小化方法对构造的机械故障特征提取优化问题进行求解,同时充分利用带状稀疏矩阵的特点,提出了具有高计算效率的迭代收敛算法流程[6]。将所提出的稀疏优化特征提取算法以滚动轴承的故障诊断为应用对象,分别分析了轴承实验台与电力机车的实际案例,稀疏有效地提取出了微弱的故障特征,验证了方法的有效性。

1 问题描述和模型构造

1.1 符号定义

本文提出的稀疏优化理论是基于l1范数正则化进行构建的,l1范数定义为

(1)

式中:s={s(n)|n=0,1,…,N-1}是定义在RN空间中的一个离散时间序列。序列s的一阶有限差分Δ(1)(s,m)和二阶有限差分Δ(2)(s,m)分别为

(2)

Δ(2)(s,m)=s(m+1)-2s(m)+s(m-1)

(3)

对于离散时间序列,定义如下两个差分矩阵

(4)

(5)

1.2 问题描述和模型构造

令w、x、y都是RN的离散时间序列,并且满足

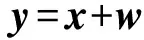
(6)

式中:w为服从高斯分布的白噪声序列;x为隐藏在背景噪声中的机械故障特征;y为观测到的含噪声信号序列。

为了从观测数据y中提取稀疏故障特征x,构造如下的凸优化问题

(7)

式中:F(x)为目标函数,由两部分组成,第1部分为数据保真度度量算子,用于度量x={x(n)}和y={y(n)}的差异,第2部分为正则项(惩罚函数);参数λ是正则化参数,用于调节组成目标函数的两部分在优化中所占的权重,其取值应满足λ>0,取值设定一般与信号中噪声的标准差成比例。式(7)中的稀疏矩阵G应该根据待提取的有用特征信号x的特点具体设定,如x的系数本身具有稀疏性,则G可取为单位矩阵,此时式(7)处理信号时相当于软阈值收缩降噪[7];如x是逐段恒定的信号,则G可取为式(4)中定义的一阶微分矩阵操作算子,此时式(7)就是经典的总变分(全变分)降噪方法[8]。

2 受控极小化方法

受控极小化适用于解决那些直接求解比较困难的优化问题。受控极小化方法并不直接极小化式(7)中的目标函数F(x),相反地,它求解一系列的优化问题,记为Qk(x,xk),k=0,1,2,…。这种思路的出发点就是求解Qk(x,xk)比直接求解F(x)要简单。受控极小化方法通过极小化Qk(x,xk)获得相应的序列值xk。

MM方法中要求Qk(x,xk)是凸函数,并且是目标函数F(x)的受控优化算子,即满足如下约束

图1所示为极小化单变量函数的MM方法的执行过程,图中x0为初始值。由图1可观察到Q0(x,x0)在x0处与F(x)在此处的取值相等,其余值大于F(x)在相应处的值。第1次迭代时,通过极小化Q0(x,x0)得到下一次迭代的初始值x1,即Q1(x,x1)在x1处与F(x)在此处的取值相等。通过类似的反复迭代,最终收敛于目标函数F(x)的最小值。以此类推,可以得到MM方法用于求解多变量函数的极小化。由于MM方法使用简单、计算高效,因此在多变量的优化求解中其作用更加突出。

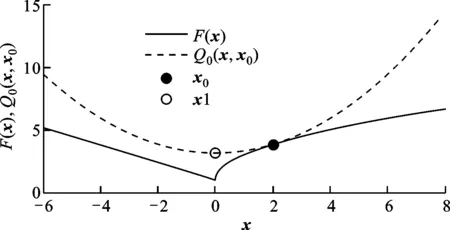
图1 极小化单变量函数的MM方法的执行过程

综上所述,利用MM方法求解目标函数F(x)可以概括为以下步骤:

(1)令k:=0,初始化x0;

(2)构造合适的Qk(x,xk)使其满足式(8)和式(9)中的约束;

(3)记Qk(x,xk)的极小值为xk+1,即

(10)

(4)令k:=k+1,转步骤(2)。

3 算法推导

采用MM方法求解式(7)中定义的优化问题,一种通用的方法是在构造便于优化的Qk(x,xk)(即受控优化算子)时利用二次函数代替式(7)中的正则项。此时,目标函数F(x)的优化问题就转化为二次项优化问题,可以通过求解一系列的线性方程组得到解决。

对于x的l1范数,构造满足式(8)和式(9)中的约束条件的函数如下

(11)

式(11)可以更简便地表示如下

(12)

式中:Λk为对角矩阵,定义为Λk:=diag(|xk|)。

由Gx代换式(12)中的变量x,得到

(13)

此时,对角矩阵Λk:=diag(|Gxk|)。

利用式(13),可以得到式(7)中目标函数F(x)的Majorizer,即

(14)

式中:对角矩阵Λk:=diag(|Gxk|)。采用受控极小化方法,通过极小化式(12)中的Qk(x,xk)得到xk+1,其解析解为

(15)

式(15)中的对角矩阵Λk里的部分元素可能会随着Gxk收缩到0而趋于无穷大。因此,需要对式(15)进行适当的改写,使其避免产生上述问题。利用矩阵求逆引理[9],式(15)等价于

(16)

式(16)中需要对线性方程组进行求解,通常这样的求解在y点数较多时计算量会比较大。然而,稀疏矩阵G通常选取为带状矩阵,则式(16)中需要求逆的部分也是带状矩阵。此时式(16)中的线性系统可以进行高效的求解。算法的具体计算步骤归纳如下。

输入:y∈RN,λ,G;

初始化:x=y;

步骤1:通过式(16)计算xk+1;

步骤2:令xk:=xk+1,转步骤1,直到收敛;

步骤3:输出x。

4 仿真验证

为了检验本文提出的稀疏优化特征提取算法在周期性冲击故障特征提取中的有效性和实用性。现模拟了一组周期性冲击信号,其中的冲击单元为

(17)

令采样频率fs=1 kHz,信号采样长度L=2 048。为了模拟工程实践中普遍存在的背景噪声,对原信号加入了高斯白噪声,信噪比为-3 dB。两信号的波形如图2所示。

(a)周期性冲击信号

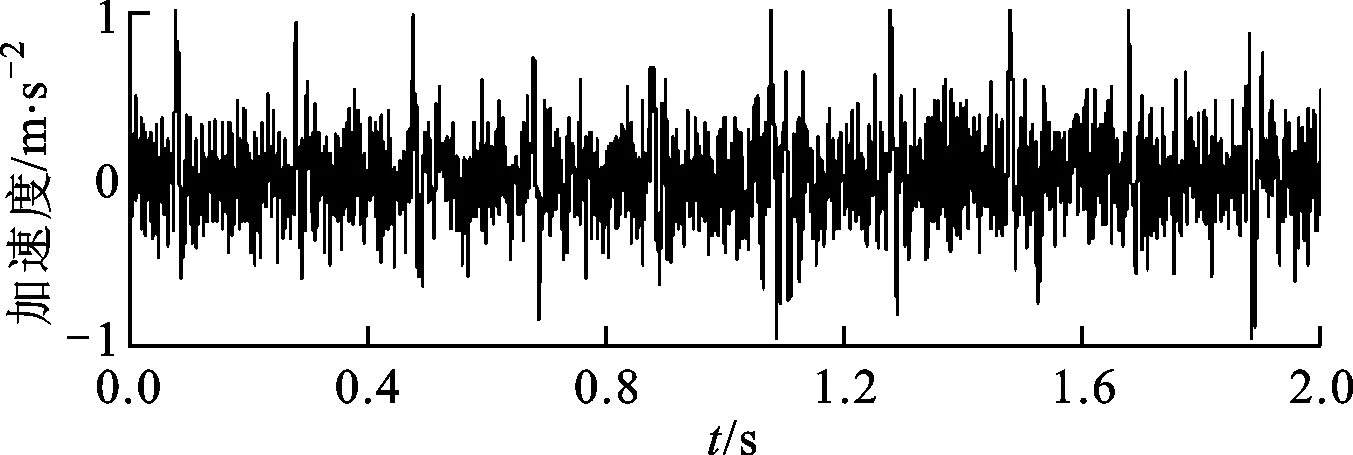
(b)含噪声的观测信号图2 仿真信号波形图

采用本文提出的稀疏优化特征提取算法对该含噪信号进行分析,其中正则化参数设置为λ=0.66,矩阵G选取为式(5)中定义的二阶差分矩阵D(2),算法迭代次数为20,分析结果及算法收敛特性分别如图3和图4所示。在图3中可以很清晰地发现,以0.2 s(对应的频率为5 Hz)为时间间隔的周期性冲击单元,与仿真冲击信号相一致。因此,本文提出的稀疏优化特征提取算法可以有效地提取微弱冲击故障特征,同时对噪声也有很强的抑制作用。从图4中可以观察到,优化的目标函数随着算法迭代次数的增加而逐步收敛于最优解。

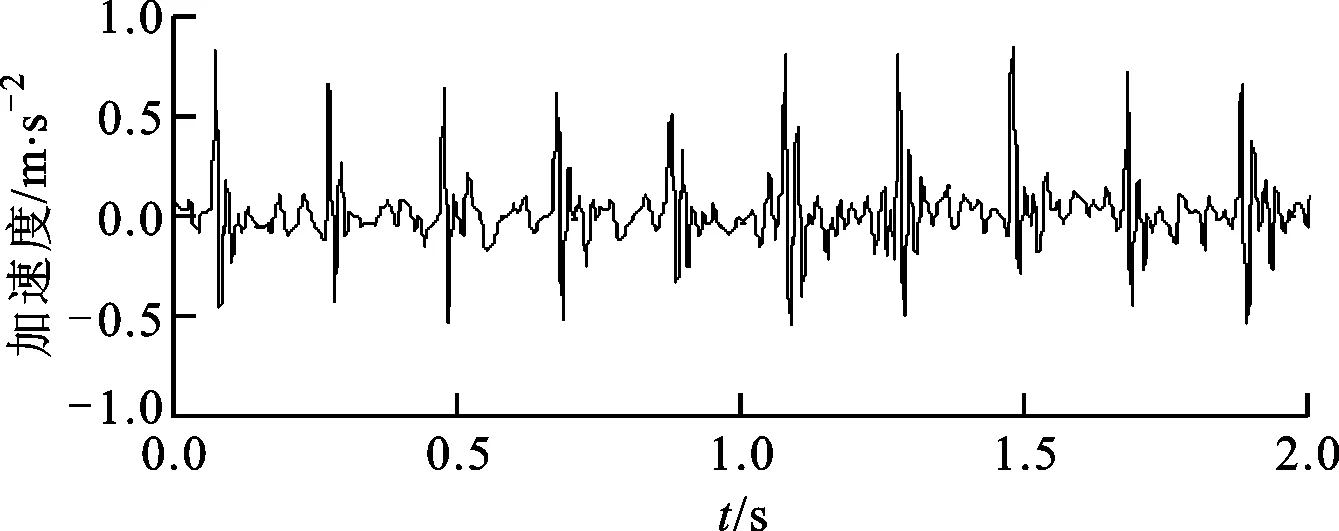
图3 提取出的波形

图4 目标函数随迭代次数的变化

5 工程应用

滚动轴承是关键设备中应用最为广泛的一种通用机械部件,同时也是一种易损部件,其一旦出现故障,不仅会影响系统的正常运行,而且严重时还会导致重大的恶性事故。因此,为了确保设备运行安全,对具有重要用途的轴承进行有效的故障诊断是非常必要的[10]。为验证所提出的稀疏优化特征提取方法在机械微弱故障特征提取中的有效性,本文将其应用于实测的轴承故障振动信号分析中。

5.1 实验背景说明

采用美国凯斯西储大学轴承数据中心的滚动轴承故障模拟实验台数据进行实验验证分析。实验平台如图5所示,包括1台电动机,1个扭矩传感器/译码器,1个功率测试计,还有电子控制器(图中没显示)。被测试轴承支承电机轴,驱动端滚动轴承型号为SKF 6205,使用电火花加工技术在轴承上布置了单点故障。实验中转速为1 730 r/min,采样频率为12 kHz。表1中列出了轴承各部件的故障频率倍数,计算得到轴承外圈故障特征频率为103.4 Hz,内圈故障特征频率为156.1 Hz。

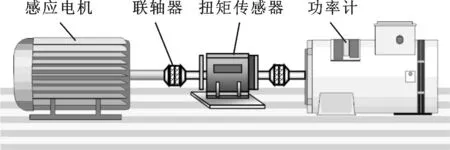
图5 轴承测试实验平台结构示意图

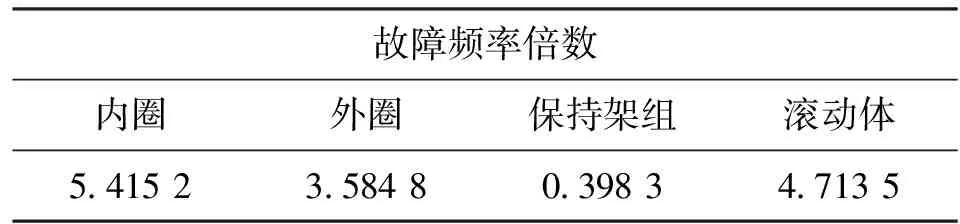
故障频率倍数内圈外圈保持架组滚动体54152358480398347135

图6所示为在电机壳体的驱动端上采集的外圈故障振动信号的时域波形图。采用本文提出的稀疏优化特征提取算法对该含噪信号进行分析,设置正则化参数λ=0.56,矩阵G选取为单位矩阵,算法迭代次数为20,分析结果如图7所示。在提取得到的特征波形图中可以很清晰地发现周期性冲击单元,与外圈故障特征频率相一致。

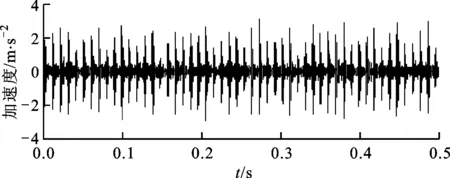
图6 外圈故障轴承振动加速度信号的时域波形

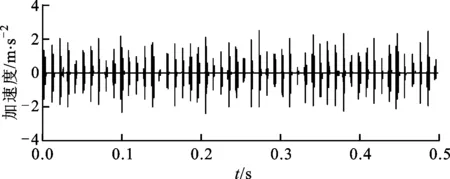
图7 外圈故障轴承振动信号特征提取波形

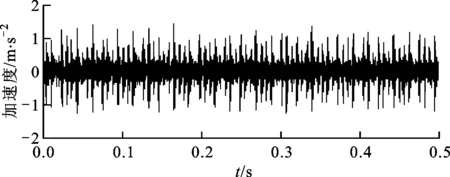
图8 内圈故障轴承振动加速度信号的时域波形

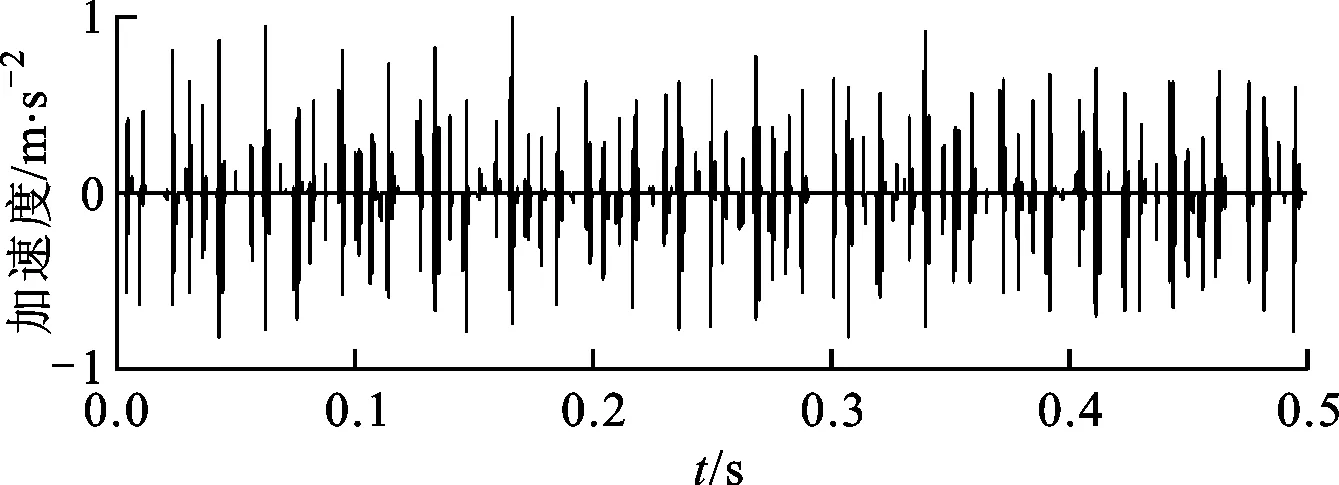
(a)提取出来的波型

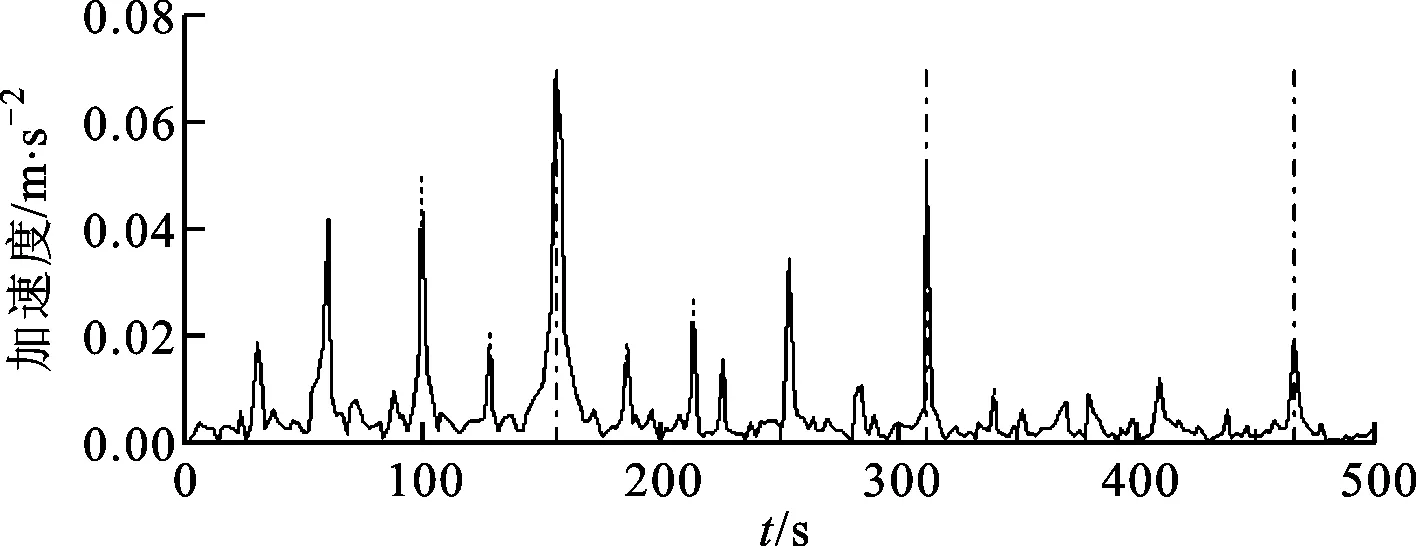
(b)包络谱图9 内圈故障轴承振动信号特征提取波形及其包络谱

图8所示为在电机壳体的驱动端上采集的内圈故障振动信号的时域波形图。采用本文提出的稀疏优化特征提取算法进行分析,设置正则化参数λ=0.46,其余参数设置与外圈故障分析一致,分析结果及其包络谱如图9所示。在图9a中可以很清晰地发现周期性冲击单元与内圈故障特征频率相一致。从图9b中可以清晰地观察到存在内圈故障特征频率及其倍频的谱峰(图中红色的点划线),同时周围还伴随着转频及其谐波成分的边频带(图中绿色的虚线)。分析结果与轴承内圈存在局部故障时的振动信号特征相一致[11]。

将本文所提出的算法应用于同型号同转速下正常滚动轴承的信号分析中,振动信号时域波形如图10所示,可以观察到正常轴承振动信号振幅明显低于故障轴承振动信号。采用本文提出的算法对该振动信号进行分析,设置正则化参数λ=0.21,矩阵G选取为单位矩阵,算法迭代次数为20,分析结果如图11所示。本文分析结果显示,所提出的算法可以将正常轴承振动信号中大量随机噪声滤除,消噪效果较好,同时还不会产生伪故障冲击特征。

图10 正常轴承振动加速度信号的时域波形

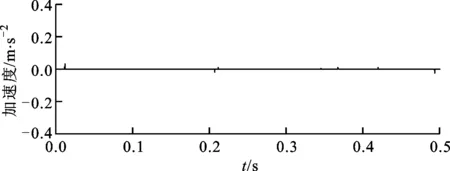
图11 正常轴承振动信号特征提取波形

5.2 稀疏分析结果与对比

将本文提出的算法应用于某电力机车的滚动轴承的外圈轻微损伤故障诊断。轴承置于测试机车轴承的某实验装置上,轴承型号为52732QT,具体参数见表2,其中接触角为0。实验中采样频率为12.8 kHz,轴承转速为481 r/min,数据长度为4 096,通过计算得到轴承外圈故障特征频率为57.8 Hz。

表2 测试滚动轴承具体参数

利用加速度传感器采集的振动数据如图12所示。时域信号中可以观察到噪声比较大,看不到明显的冲击信号。利用本文提出的算法对该含噪声信号进行分析,设置正则化参数λ=0.4,矩阵G选取为式(5)中定义的二阶差分矩阵D(2),算法迭代次数为20,提取特征波形及其包络谱如图13所示。从图13a中可以很清晰地发现间隔约为17.1 ms的周期性冲击单元,其对应的频率为58.5 Hz,与计算得到的外圈故障特征频率57.8 Hz相一致。图13b中存在很明显的外圈故障特征频率57.8 Hz及其倍频成分。

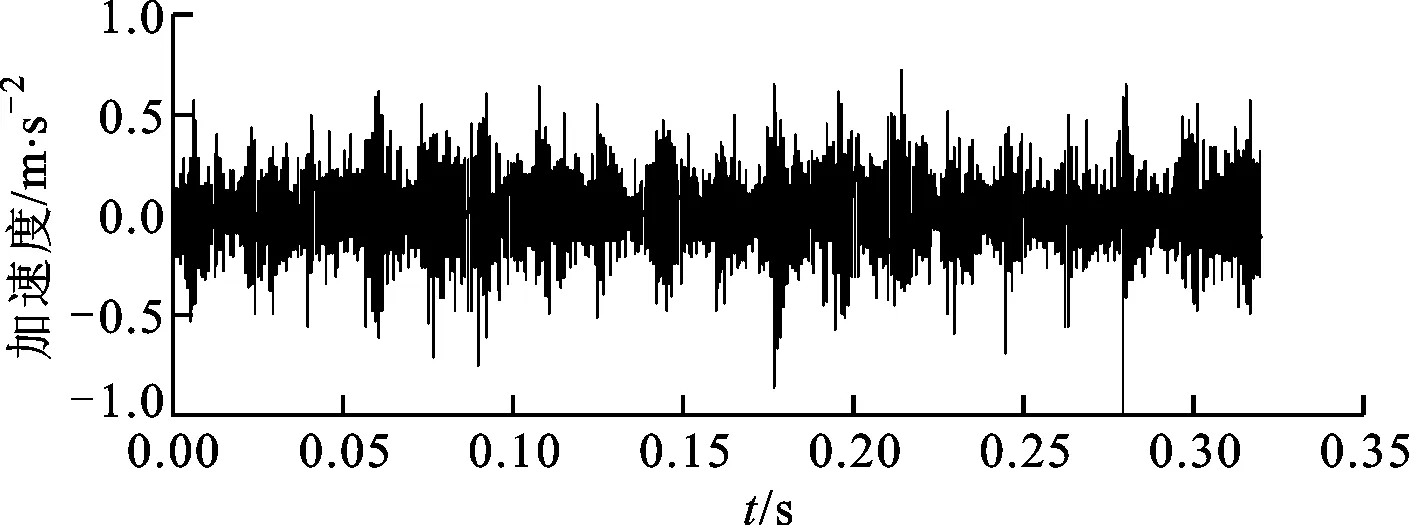
图12 故障轴承振动加速度信号的时域波形

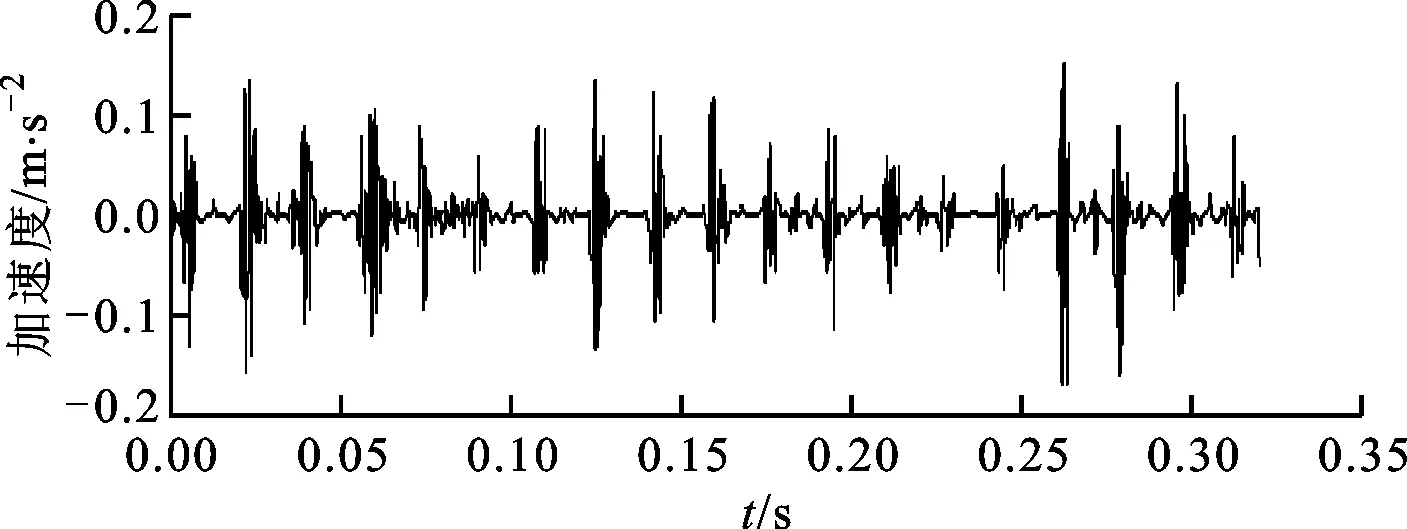
(a)提取出来的波形

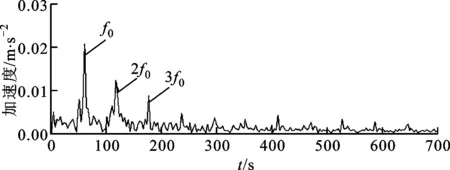
(b)包络谱图13 故障轴承振动信号特征提取波形及其包络谱

6 结 论

(1)本文针对机械故障诊断中微弱故障特征提取的难题,构造了有效的稀疏优化目标函数,该目标函数中的正则项(惩罚函数)可根据待分析信号特征灵活调节,实现分析结果的最大稀疏化。

(2)引入受控极小化方法进行求解所构造的目标函数。利用受控极小化方法对构造的机械故障特征提取优化问题进行求解,同时充分地利用带状稀疏矩阵的特点,提出了高效的迭代收敛算法,便于在工程中推广应用。

(3)本文提出的稀疏优化模型及算法可以拓展到其他变换域,处理变换得到的表征信号的系数,如短时傅里叶变换系数和小波变换系数;该稀疏优化算法也可以作为后处理工具与现有的方法进行结合,如基于小波的收缩降噪法。

(4)将所提出的稀疏优化特征提取算法以滚动轴承的故障诊断为应用对象,分别分析了轴承实验台与电力机车的实际案例,从振动信号中稀疏有效地提取出了微弱故障特征,验证了算法的有效性。

[1] LEI Y G, LIN J, ZUO M J, et al. Condition monitoring and fault diagnosis of planetary gearboxes: a review [J]. Measurement, 2014, 48: 292-305.

[2] MALLAT S. A wavelet tour of signal processing: the sparse way [M]. New York, USA: Academic Press, 2008: 292-305.

[3] HE Wangpeng, ZI Yanyang, CHEN Binqiang, et al. Automatic fault feature extraction of mechanical anomaly on induction motor bearing using ensemble super-wavelet transform [J]. Mechanical Systems and Signal Processing, 2015, 54: 457-480.

[4] HE Wangpeng, ZI Yanyang, CHEN Binqiang, et al. TunableQ-factor wavelet transform denoising with neighboring coefficients and its application to rotating machinery fault diagnosis [J]. Science China Technological Sciences, 2013, 56(8): 1956-1965.

[5] CHEN Binqiang, ZHANG Zhousuo, ZI Yanyang, et al. Detecting of transient vibration signatures using an improved fast spatial-spectral ensemble kurtosis kurtogram and its applications to mechanical signature analysis of short duration data from rotating machinery [J]. Mechanical Systems and Signal Processing, 2013, 40(1): 1-37

[6] FIGUEIREDO M A, BIOUCAS-DIAS J M, NOWAK R D. Majorization-minimization algorithms for wavelet-based image restoration [J]. IEEE Transactions on Image Processing, 2007, 16(12): 2980-2991.

[7] AFONSO M V, BIOUCAS-DIAS J M, FIGUEIREDO M A. Fast image recovery using variable splitting and constrained optimization [J]. IEEE Transactions on Image Processing, 2010, 19(9): 2345-2356.

[8] CONDAT L. A direct algorithm for 1D total variation denoising [J]. IEEE Signal Processing Letters, 2013, 20(11): 1054-1057.

[9] TYLAVSKY D J, SOHIE G R L. Generalization of the matrix inversion lemma [J]. Proceedings of the IEEE, 1986, 74(7): 1050-1052.

[10]何正嘉, 訾艳阳, 陈雪峰, 等. 内积变换原理与机械故障诊断 [J]. 振动工程学报, 2007, 20(5): 528-533. HE Zhengjia, ZI Yanyang, CHEN Xuefeng, et al, Transform principle of inner product for fault diagnosis [J]. Journal of Vibration Engineering, 2007, 20(5): 528-533.

[11]RANDALL R B, JEROME A. Rolling element bearing diagnostic: a tutorial [J]. Mechanical Systems and Signal Processing, 2011, 25(2): 485-520.

(编辑 杜秀杰)

Majorization Minimization Oriented Sparse Optimization Method for Feature Extraction Technique in Machinery Fault Diagnosis

HE Wangpeng1,2,ZI Yanyang1,CHEN Binqiang3

(1. State Key Laboratory for Manufacturing Systems Engineering, Xi’an Jiaotong University, Xi’an 710049, China; 2. Polytechnic School of Engineering, New York University, New York 11201, USA; 3. School of Aerospace Engineering, Xiamen University, Xiamen, Fujian 361005, China)

To deal with the effective representation and extraction of incipient transient features of mechanical fault, a general sparsity based identification approach is proposed. This approach designs a sparsity optimization function that integrates impulsive feature preserving factor and penalty function factor, and takes the regularization parameter into consideration such as to address the actual factor weights in different situations. The majorization minimization is introduced to simplify the designed function into a series of convex optimization problems. A finite difference based numerical iterative method is developed for the proposed approach, and its fast convergence and numerical stability are illustrated. The proposed approach is versatile to digital signal processing of mechanical fault detecting practices, and is applied to bearing fault identifications in lab. It is shown that no matter in high or low noise backgrounds, the impulsive components are significantly enhanced, which can be verified in the dominant energy ratios of characteristic frequencies in the Hilbert envelope spectrum. This approach is also utilized to conduct bearing fault diagnosis of traction part of electrical locomotive, and the impulsive features masked by heavy colored noises are effectively detected in time domain and spectral domain.

sparse representation; convex optimization; majorization minimization; feature extraction; fault diagnosis

2015-08-11。 作者简介:贺王鹏(1989—),男,博士生;訾艳阳(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(51275384);福建省重大科技项目(2014H6025);福建省高端装备制造协同创新中心资助项目。

时间:2015-12-30

10.7652/xjtuxb201604015

TH17

A

0253-987X(2016)04-0094-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20151230.1814.004.html