一种相位编码信号及其失配滤波器设计方法

徐磊磊,臧会凯,周生华,刘宏伟,严俊坤

(1.西安电子科技大学雷达信号处理国家重点实验室, 710071, 西安; 2.西安电子科技大学信息感知技术协同创新中心, 710071, 西安)



一种相位编码信号及其失配滤波器设计方法

徐磊磊1,2,臧会凯1,2,周生华1,2,刘宏伟1,2,严俊坤1,2

(1.西安电子科技大学雷达信号处理国家重点实验室, 710071, 西安; 2.西安电子科技大学信息感知技术协同创新中心, 710071, 西安)

为了解决相位编码信号脉冲压缩后峰值旁瓣电平过高的问题,提出了一种新颖的相位编码信号——宽主瓣相位编码信号及其失配滤波器的设计方法。首先,在给定相位编码信号时宽并且保持信号带宽不变的条件下,通过增加相位编码信号的码元长度来增加优化自由度进而降低其峰值旁瓣电平;然后,给出了宽主瓣相位编码信号的设计准则,并使用基于L-BFGS算法的最小p范数优化算法进行求解;最后,基于该相位编码信号提出了以最小化峰值旁瓣电平和逼近期望的主瓣为准则的失配滤波器设计方法,并使用凸优化算法进行求解。仿真结果表明:在给定相位编码信号的时宽、保持信号距离分辨力不变的条件下,与传统相位编码信号相比,主瓣展宽的相位编码信号峰值旁瓣电平可以降低4.32 dB;通过设计失配滤波器的方法,该相位编码信号脉冲压缩后的峰值旁瓣电平可以进一步降低5.94 dB。

相位编码信号;失配滤波器;峰值旁瓣电平;脉冲压缩

脉冲压缩技术解决了雷达作用距离和距离分辨力之间的矛盾,但脉冲压缩信号通常具有距离旁瓣,较高的距离旁瓣不利于雷达对目标进行有效探测,特别是多目标或强杂波背景下的弱目标检测,弱目标的主瓣极易被强目标回波的距离旁瓣淹没造成漏警[1],因此设计具有良好距离旁瓣特性的信号波形对提高雷达的探测性能具有重要意义。相位编码信号是一种常见的脉冲压缩信号,具有抗干扰性和隐蔽性良好以及测量精度高等优点,在MIMO雷达研究中获得广泛了研究,是一种非常有应用前景的雷达信号。

目前有2种抑制相位编码信号距离旁瓣的方法:一种是设计具有低距离旁瓣电平特性的相位编码信号[2-5],另一种是设计失配滤波器来降低距离旁瓣的峰值旁瓣电平[6-7]。通常,相位编码信号的时宽带宽积等于相位编码信号的码元长度,相位编码信号的带宽等于一个子脉冲宽度的倒数。通常可以通过增加相位编码信号的码元长度来进一步降低距离旁瓣电平,但对于时宽固定的相位编码信号,这将会增加其带宽。对于一个雷达系统,如果其信号处理带宽是固定的,此时无法通过单一的增加码元长度的方法来降低距离旁瓣电平。

针对此问题,本文提出了一种新颖的相位编码信号,简称宽主瓣连续相位编码信号。在给定相位编码信号时宽并且保持其带宽不变的条件下,通过增加码元长度来降低相位编码信号的距离旁瓣电平。本文设计的相位编码信号在脉冲宽度相同的情况下,具有相同的带宽,也就是说,与传统的相位编码信号相比,所对应时域中的主瓣变宽了,因此称这种信号为宽主瓣相位编码信号,该信号可以用于处于搜索阶段的宽带雷达系统。本文给出了宽主瓣相位编码信号的设计准则,并使用基于L-BFGS算法[8]的最小p范数[9]优化算法进行求解。为了进一步降低宽主瓣相位编码信号的距离旁瓣电平,本文研究了其失配滤波器的设计方法,给出了失配滤波器的设计准则,并使用凸优化算法进行优化。仿真结果表明,在保持相位编码信号的带宽不变的条件下,增加相位编码信号的码元长度,可以进一步降低相位编码信号脉冲压缩后的距离旁瓣电平,而且由宽主瓣相位编码信号设计的失配滤波器,在保持宽主瓣相位编码信号通过失配滤波器脉冲压缩后带宽不变的条件下,以一定的信噪比损失为代价,能够进一步降低脉冲压缩后的距离旁瓣电平。

1 宽主瓣相位编码信号设计

假设s∈CNs×1是一个码元长度为Ns的相位编码信号,则s在距离移位k处的匹配滤波结果[10]可以写为

(1)

式中:ρk,k≠0表示脉冲压缩后的旁瓣,对于传统的相位编码信号,ρ0表示信号脉冲压缩后的主瓣;Jk为移位矩阵,Jk的具体表达式为[11]

(2)

其中0为全零矩阵,I表示单位矩阵。

脉冲压缩后的旁瓣ρk满足

(3)

式中:(·)*表示取共轭。由式(3)可知,|ρk|=|ρ-k|,即主瓣的幅度关于零位移处对称,|·|表示取模值。对于传统的相位编码信号,其峰值旁瓣电平(peak sidelobe level, PSL)的定义为

(4)

对于现有的波形设计方法,波形设计的准则之一是抑制相位编码信号脉冲压缩后的峰值旁瓣电平。

为了展宽相位编码信号的主瓣,这里将k=0附近的旁瓣也作为主瓣区域。假设将ρk,k=0,±1,±2,…,±M作为主瓣区域,由于ρ0的取值不跟随s变化,并且ρk关于k=0共轭对称,因此在主瓣区域内只考虑ρk,k=1,2,…,M的取值即可。为了使设计的相位编码信号具有一个展宽的主瓣,需要在设计前确定一个期望的主瓣形状。期望的主瓣形状可以是矩形,sinc函数的主瓣形状,也可以是其他的主瓣形状。对主瓣形状的约束主要是保证设计后的相位编码信号带宽不变,而主瓣的3 dB宽度决定着信号的带宽,因此期望的主瓣幅度取至-3 dB幅度处即可。假设期望的主瓣形状记为p(p为M维的列向量且其元素为正实数),这里要求p的元素为正实数的原因是保证主瓣内的相位平稳,使设计得到的主瓣相位变化尽可能地小。

根据最小化相位编码信号的峰值旁瓣电平和逼近期望的主瓣形状,可得到宽主瓣相位编码信号的设计准则为

(5)

式中:s为相位编码信号;Ns为相位编码信号的长度;δ为人为设定的常数,表示最大可接受的主瓣失配。由于凸优化具有求解速度快、计算量小且求出结果为全局最优点等优点,通常优化问题首先考虑是否能使用凸优化进行求解。由于式(5)约束条件中sHs=Ns为非凸约束,所以不能使用凸优化进行求解。将式(5)目标函数进行转化

(6)

式中:φ为s的相位向量,即s=exp(jφ)。

对于式(6)中的优化问题,可以使用现有的极小极大算法如序列二次规划算法、梯度算法等进行优化求解,但是上述算法具有运算量大、速度慢等问题。为了进一步提高优化算法的性能,本文使用一种基于p范数的优化算法求解式(6)中的优化问题,下面进行详细介绍。将所有的旁瓣取模值后记为向量

(7)

并且将期望的主瓣与实际主瓣的差值取模值后记为

(8)

则式(6)中的目标函数可以写为‖ρs‖∞,其中‖·‖∞表示无穷范数。式(6)中的约束条件也可以写为‖eM‖∞≤δ。其实,最小化‖ρs‖∞可以通过最小化‖ρs‖p实现,伴随着p数值的增加,最小化一系列的‖ρs‖p可近似等价为最小化‖ρs‖∞,其中,‖·‖p表示p范数。同理,最小化‖eM‖∞通过最小化一系列的‖eM‖p得到。定义函数

(9)

式中:α是一个人为设定的正实数,用于折中旁瓣抑制的效果和主瓣匹配的效果。

根据上述的分析和符号定义,基于p范数的优化算法的简要流程如下:

(1)初始化,设置φ0和ε1的初始值,令i=1,p=2,μ=2,f0=100;

(2)使用φi-1作为初始值,通过使用L-BFGS算法求解最小化f(φ),求得优化结果φi,令fi=f(φi);

(3)如果|fi-1-fi|<ε1,则输出φi并停止循环,否则令p=μp,i=i+1,跳至步骤(2)。

在步骤(2)中,最小化f(φ)是一个无约束优化问题,可以使用现有的无约束优化算法进行求解,这里使用L-BFGS算法求解该问题。L-BFGS算法的具体流程[8]如下:

(1)初始化 设置L-BFGS算法的更新数目m,令迭代指示数i=0,选取初始值φ0并计算f1和f1的值,设置初始的搜索方向为g1=-f1;

(2)根据fi、fi和gi,使用线搜索算法确定步长λi;

(3)计算zi=λigi,φi+1=φi+λigi;

(5)令q=fi+1;

(6)forn=i,i-1,…,i-m+1

end

(8)forn=i-m+1,i-m+2,…,i

end

(9)gi+1=-r;

(10)i=i+1;

直至满足终止条件。

2 失配滤波器设计

2.1 信号模型

对于宽主瓣相位编码信号s∈CNs×1,假定失配滤波器系数向量h∈CNh×1,则宽主瓣相位编码信号s通过失配滤波器脉冲压缩后的输出结果可表示为

ηc=s⊗h/Ns=[η1,η2,…,ηi,…,ηNs+Nh-1]T

(10)

式中:⊗表示卷积;Nh表示失配滤波器的长度。为了方便公式推导,令Ns和Nh同为偶数或同为奇数。根据式(10)中的失配滤波器结果ηc,取出其距离旁瓣记为

(11)

式中:k∈[1,(Ns+Nh)/2-M-1];l∈[(Ns+Nh)/2+M+1,Ns+Nh-1]。同理,将输出的主瓣记为

(12)

式中:t∈[(Ns+Nh)/2-M,(Ns+Nh)/2+M]。由于相位编码信号经过失配滤波器脉冲压缩后主瓣左右两边不是对称的,将期望主瓣部分对应的函数值区间均匀地离散化为2×M+1维的列向量作为期望的主瓣bm的取值。

2.2 建立目标函数和构建目标函数的约束条件

首先将宽主瓣相位编码信号s首尾对称补零,扩展成长度为Nh的宽主瓣相位编码信号

(13)

(14)

根据最小化宽主瓣相位编码信号通过失配滤波器脉冲压缩后的峰值旁瓣电平和逼近期望的主瓣形状,可得到失配滤波器的设计准则为

(15)

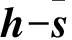
3 仿真实验及结果

仿真参数设置,设相位编码信号的时宽为15.36 μs,采样频率为100 MHz,对信号进行了采样,此时相对时延最小间隔为采样频率的倒数,即0.01 μs。为了进行对比,假设增加码元长度之前的相位编码信号码元长度N1=64,期望的主瓣为该码元长度N1=64的相位编码信号的主瓣。限于篇幅原因,现给出N1=64的相位编码信号前20位的相位值:-31.52°,-174.94°,26.29°,-155.35°,59.02°,-113.26°,165.48°,-4.52°,-21.52°,140.17°,52.85°,172.50°,-131.23°,-160.32°,-61.22°,-12.56°,26.37°,144.33°,106.58°。

3.1 设计宽主瓣相位编码信号

设计宽主瓣相位编码信号s的码元长度Ns=256,相位编码信号的主瓣宽度控制量M=4,权系数α=0.1,利用基于L-BFGS算法的最小p范数优化算法进行优化,得到码元长度为256的宽主瓣相位编码信号。通常情况下,信号脉冲压缩后主瓣3 dB的宽度决定着信号的带宽,故对比信号脉冲压缩后主瓣3 dB宽度即可。

采用本文方法设计的宽主瓣相位编码信号脉冲压缩后的主瓣区域幅值和期望的主瓣区域幅值如图1所示。由图1可知,设计的宽主瓣相位编码信号脉冲压缩后的主瓣区域幅值和期望的主瓣区域幅值基本重合,因此本文方法设计得到的宽主瓣脉冲压缩后信号带宽保持不变。

采用本文方法设计的宽主瓣相位编码信号的主瓣区域的相位和期望主瓣区域的相位如图2所示。由图2可知,设计的宽主瓣相位编码信号的主瓣区域相位变化范围为[-0.164°,0.164°],而期望主瓣区域相位变化范围为[-0.414°,0.414°],可以看出所设计的宽主瓣相位编码信号主瓣区域相位波动范围更小,更有利于雷达脉冲压缩后的相干积累。

采用本文方法设计的宽主瓣相位编码信号脉冲压缩后输出的结果和码元长度N1=64的相位编码信号脉冲压缩后输出的结果如图3所示。由图3可知,码元长度N1=64的相位编码信号脉冲压缩后输出的峰值旁瓣电平为-32.66 dB,设计的宽主瓣相位编码信号脉冲压缩后输出的峰值旁瓣电平为-36.98 dB,峰值旁瓣电平降低了4.32 dB,因此本文方法设计得到的宽主瓣相位编码信号在保证信号带宽不变的情况下,可以进一步降低脉压后的峰值旁瓣电平。限于篇幅原因,现给出Ns=256的相位编码信号前20位的相位值:-80.21°,-115.85°,-78.26°,-68.77°,-6.41°,-19.41°,-26.84°,41.80°,63.09°,78.85°,133.65°,-151.89°,-146.60°,-129.54°,177.01°,-174.24°,-170.89°,-157.62°,-119.03°,-98.50°。

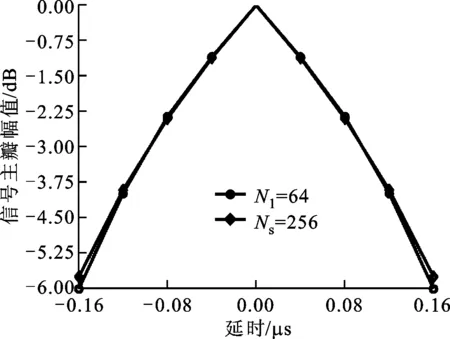
图1 匹配滤波脉冲压缩后的主瓣区域幅值曲线

图2 匹配滤波脉冲压缩后的主瓣区域相位曲线

图3 不同信号脉冲压缩输出结果

3.2 由宽主瓣相位编码信号设计失配滤波器

通常,失配滤波器的长度越长,信号经过失配滤波器脉冲压缩后的峰值旁瓣电平会越低,但信噪比损失和计算量会随着失配滤波器长度的增加而增大,因此实际应用中需要综合折中考虑这两方面的因素。本文仿真实验失配滤波器的长度Nh=512,主瓣宽度控制量M=4,权系数β=0.3,失配系数ε=2.25,利用凸优化工具箱cvx求解,得到失配滤波器系数h。

宽主瓣相位编码信号经过本文设计的失配滤波器脉冲压缩后的主瓣区域幅值和期望主瓣区域幅值如图4所示。由图4可知,宽主瓣相位编码信号经过所设计的失配滤波后的主瓣区域幅值和期望主瓣区域幅值基本重合,因此宽主瓣相位编码信号经过所设计的失配滤波器脉冲压缩后带宽保持不变。

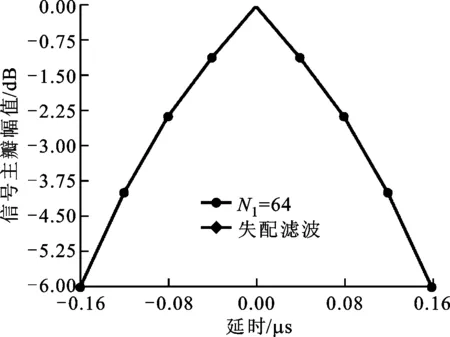
图4 失配滤波脉冲压缩后的主瓣区域幅值曲线

宽主瓣相位编码信号经过本文设计的失配滤波器脉冲压缩后的主瓣区域的相位和期望主瓣区域的相位如图5所示。由图5可知,宽主瓣相位编码信号经过本文设计的失配滤波器脉冲压缩后的主瓣区域的相位范围为[(-7.207×10-9)°,(-7.207×10-9)°],而期望主瓣区域相位变化范围为[-0.414°,0.414°],设计的宽主瓣相位编码信号的主瓣区域相位变化范围为[-0.164°,0.164°]。可以看出,宽主瓣相位编码信号经过本文设计的失配滤波器脉冲压缩后的主瓣区域的相位波动范围几乎为0,更加有利于脉冲压缩后的相干积累。

图5 失配滤波脉冲压缩后的主瓣区域相位曲线

图6为宽主瓣相位编码信号经本文设计的匹配滤波器和失配滤波器脉冲压缩后的输出结果。由图6可知,宽主瓣相位编码信号的脉冲压缩后输出的峰值旁瓣电平为-36.98 dB,宽主瓣相位编码信号经过本文设计的失配滤波器脉冲压缩后输出的峰值旁瓣电平为-42.92 dB,峰值旁瓣电平降低了5.94 dB,信噪比损失了0.085 dB。因此,宽主瓣相位编码信号经过本文设计的失配滤波器脉冲压缩后可在保证带宽不变的同时,以极小的信噪比损失为代价,进一步降低脉冲压缩后的峰值旁瓣电平。

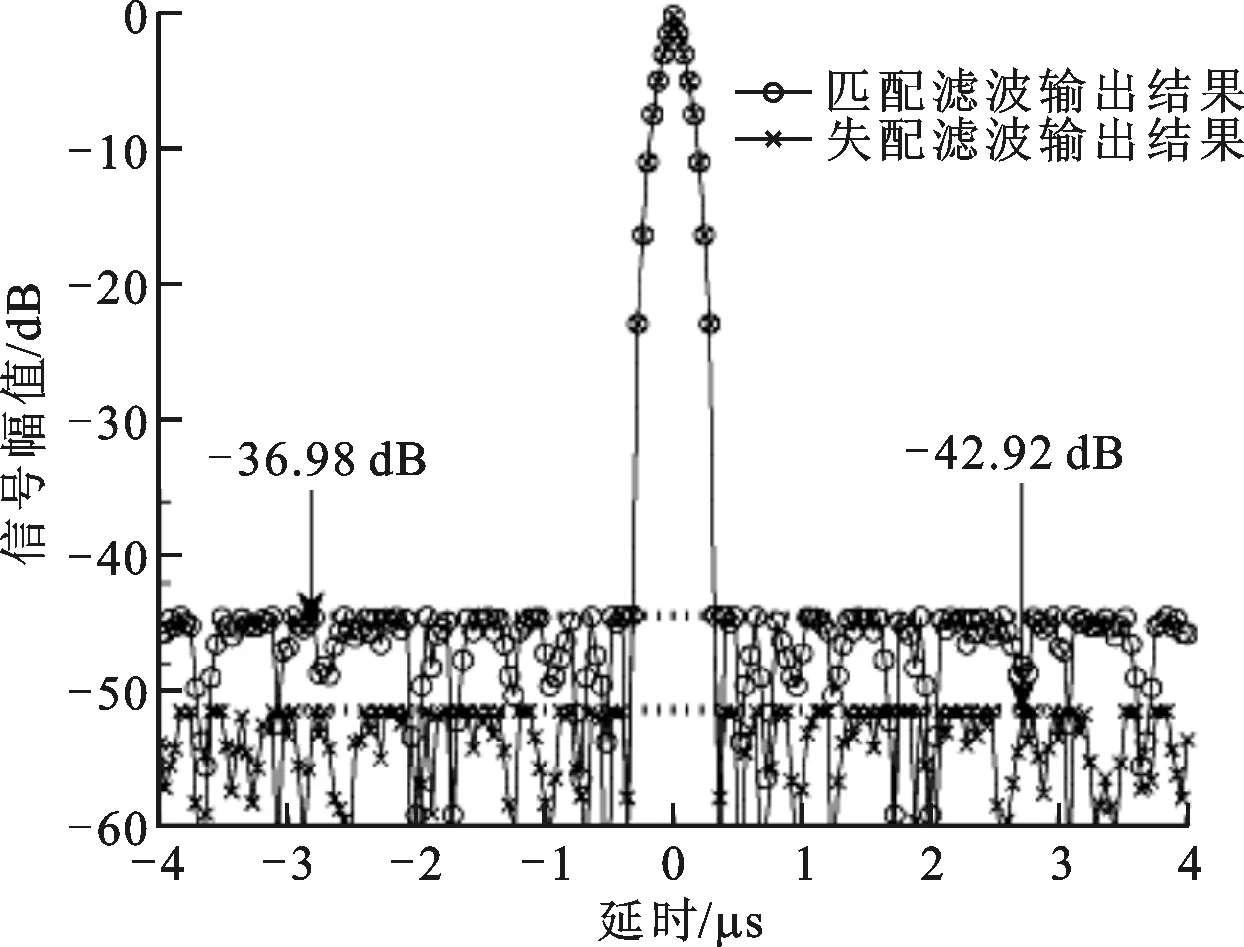
图6 不同信号脉冲压缩输出结果

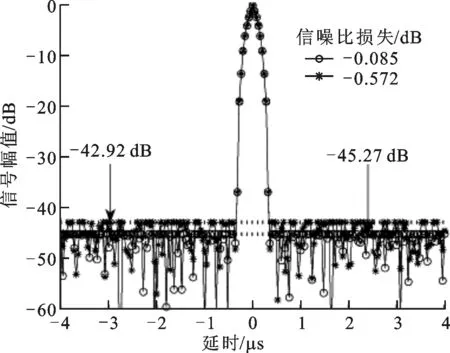
图7 不同信噪比损失脉冲压缩输出结果

图7为本文所设计的宽主瓣相位编码信号和失配滤波器在不同信噪比损失条件下脉冲压缩后输出的结果,其中信噪比损失为0.572 dB对应的宽主瓣相位编码信号的失配系数。从图7可以看出,在主瓣逼近程度相同的条件下,信噪比损失越大,脉冲压缩后的峰值旁瓣电平越低。但是,如果信噪比损失过大,会严重影响到雷达的探测以及参数估计等性能,在实际应用中应折中考虑这两方面的影响。

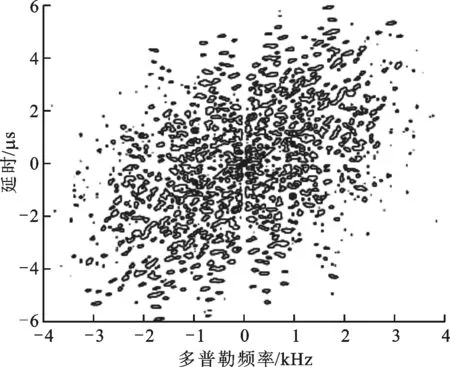
图8 失配滤波后的模糊函数图

图8为本文所设计的宽主瓣相位编码信号和失配滤波器脉冲压缩后的模糊函数图,由图8可见模糊函数图具有图钉形状,表明宽主瓣相位编码信号对速度比较敏感。因此,在存在多普勒频移的情况下,失配滤波器的性能将下降,对多普勒频移依然敏感。这是因为本文在设计宽主瓣相位编码信号及其失配滤波器时,代价函数中并未考虑多普勒敏感的问题。为了缓解多普勒敏感的问题,在实际应用中,可以采用多个失配滤波器通道对多普勒频移进行补偿。

4 结束语

本文提出了一种相位编码信号及其失配滤波器设计的方法。在给定相位编码信号时宽并且保持带宽不变的条件下,先通过增加相位编码信号的码元长度来增加优化自由度,进而降低峰值旁瓣电平,以最小化相位编码信号峰值旁瓣电平和逼近期望的主瓣形状为准则,并使用基于L-BFGS算法的最小p范数优化算法进行求解得到宽主瓣的相位编码信号;然后以最小化宽主瓣相位编码信号通过失配滤波器脉冲压缩后峰值旁瓣电平和逼近期望的主瓣形状为目标函数,以信噪比损失为约束条件,使用凸优化算法优化得到失配滤波器。仿真结果表明,与传统相位编码信号相比,在给定相位编码信号时宽并保证脉冲压缩后带宽不变的条件下,设计得到的宽主瓣相位编码信号具有低峰值旁瓣电平特性,并且由宽主瓣相位编码信号设计得到的失配滤波器在一定的信噪比损失的条件下,可以进一步降低宽主瓣相位编码信号经过失配滤波脉冲压缩后的峰值旁瓣电平。

[1] AKBARIPOUR A, BASTANI M H. Range sidelobe reduction filter design for binary coded pulse compression system [J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(1): 348-359.

[2] 杜晓林, 苏涛, 朱文涛, 等. 一种多输入多输出雷达相位编码信号的设计方法 [J]. 西安交通大学学报, 2014, 48(12): 93-99. DU Xiaolin, SU Tao, ZHU Wentao, et al. A design method for multi-Input multi-Output radar phase coding signal [J]. Journal of Xi’an Jiaotong University, 2014, 48(12): 93-99.

[3] BLUNT S D, SHACKELFORD A K, GERLACH K. Doppler compensation & single pulse imaging using adaptive pulse compression [J]. IEEE Transactions on Aerospace and Electronic Systems, 2009, 45(2): 647-659.

[4] SCHMIDT K. Binary sequences with small peak sidelobe level [J]. IEEE Transactions on Information Theory, 2012, 58(4): 2512-2515.

[5] 杜晓林, 王旭, 苏涛, 等. MIMO雷达正交相位编码信号的代数设计方法 [J]. 西安电子科技大学学报, 2014, 41(2): 64-70. DU Xiaolin, WANG Xu, SU Tao, et al. Orthogonal phase coding signal design for MIMO radar via an algebraic method [J]. Journal of Xidian University, 2014, 41(2): 64-70.

[6] NUNN C. Constrained optimization applied to pulse compression codes and filters [C]∥Proceeding of IEEE 2005 International Radar Conference. Piscataway, NJ, USA: IEEE, 2005: 190-194.

[7] CARROLL N, KRETSCHMER F F. Performance of pulse compression code and filter pairs optimized for loss and integrated sidelobe level [C]∥Proceedings of IEEE 2007 International Radar Conference. Piscataway, NJ, USA: IEEE, 2007: 110-115.

[8] WANG Yongchao, WANG Xu, LIU Hongwei, et al. On the design of constant modulus probing signals for MIMO radar [J]. IEEE Transactions on Signal Processing, 2012, 60(8): 4432-4438.

[9] ANTONIOU A, LU W S. Practical optimization: algorithm and engineering applications [M]. Berlin, Germany: Springer, 2007.

[10]ZHOU Shenghua, LIU Hongwei, WANG Xu, et al. MIMO radar range-angular-Doppler sidelobe suppression using random space-time coding [J]. IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(3): 2047-2060.

[11]SONG Xiufeng, ZHOU Shengli, WILLETT P. Reducing the waveform cross correlation of MIMO radar with space-time coding [J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4213-4224.

[12]GRANT M, BOYD S, YE Y. CVX: Matlab software for disciplined convex programming [CP/OL]. [2015-03-12]. http: ∥www.stanford.edu/～boyd/cvx.

(编辑 刘杨)

A Design Method of Phase Coded Waveform and Its Mismatched Filter

XU Leilei1,2,ZANG Huikai1,2,ZHOU Shenghua1,2,LIU Hongwei1,2,YAN Junkun1,2

(1. National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China; 2. Collaborative Innovation Center of Information Sensing and Understanding at Xidian University, Xi’an 710071, China)

A design method of phase coded waveform (called phase coded waveform with expanded mainlobe) and its mismatched filter are proposed to solve the problem that the peak sidelobe level (PSL) of phase coded waveforms after pulse compression is too high. More degrees of freedom in optimization process are obtained by increasing the code number of the phase coded waveform under a constant bandwidth at a given time width of the phase coded waveform, and then the PSL is decreased. A criterion for designing phase coded waveform with expanded mainlobe is presented, and the least-pth norm optimization algorithm with the L-BFGS is used as a sub-algorithm to solve the problem. Then, a method of designing the mismatched filter based on the designed phase coded waveform is presented to suppress the PSL and to match the desired mainlobe, and a convex optimization algorithm is used to solve the problem. Simulation results and a comparison with the traditional phase coded waveform show that under the given time width of the phase coded waveform, the PSL of the phase coded waveform with expanded mainlobe is reduced by 4.32 dB. When the method of designing the mismatched filter is used, the PSL of the phase coded waveform after pulse compression is further reduced by 5.94 dB.

phase coded waveform; mismatched filter; peak sidelobe level; pulse compression

2015-08-25。 作者简介:徐磊磊(1989—),男,博士生;刘宏伟(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61401329);国家杰出青年科学基金资助项目(61525105);中国博士后科学基金资助项目(2015 M580817)。

时间:2016-01-13

10.7652/xjtuxb201604009

TN957

A

0253-987X(2016)04-0054-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160113.1959.010.html