高超声速再入飞行器轨迹优化算法评估策略

董春云,蔡远利

(西安交通大学电子与信息工程学院, 710049, 西安)

ω=[0.091 9,0.046 0,0.165 9,0.110 0,

0.044 4,0.060 4,0.076 5,0.060 2,

0.068 9,0.068 9,0.206 9]T



高超声速再入飞行器轨迹优化算法评估策略

董春云,蔡远利

(西安交通大学电子与信息工程学院, 710049, 西安)

针对高超声速再入飞行器轨迹优化算法种类多样、决策者难以优选的问题,提出了一种轨迹优化算法综合评估策略。该策略首先对算法本身的稳定性、实时性以及优化结果的可行性、安全性、过渡性、最优性等性能进行指标建模,建立优化算法综合评估指标体系;然后基于层次分析法中的两两比较判断矩阵,以欧氏距离与违例次数为精度衡量依据,将指标权重的计算转化为一类优化问题并利用遗传算法求解;之后计算加权规范化决策矩阵,综合算法数据与理想对照组在空间距离与曲线形状两方面的贴近度,提出一种灰色逼近理想解排序加权法,最终完成评估分析过程。仿真结果表明:该策略以客观数据的形式实现了轨迹优化算法的性能量化,形成了不同算法之间统一的对比评估标准,能够帮助决策者快速遴选出适合任务需求的最优算法,避免了过程中的盲目性与主观性。

高超声速再入;轨迹优化;算法评估

飞行轨迹设计是高超声速飞行器制导与控制领域中的核心问题,也是滑翔再入飞行器总体概念设计阶段的一项重要工作,关系到飞行任务的成败[1]。为了尽可能地提高飞行器的性能,需要通过一定的优化方法设计出一条或一组安全可行的方案飞行轨迹,在真实飞行环境中由制导控制系统实时跟踪最优轨迹。由于高超声速再入飞行固有的多状态、时变、非线性和强约束等复杂特性,因此其轨迹优化过程一般只能得到近似的数值最优解。对于该类轨迹优化问题,其求解算法多种多样,性能也各有千秋。设计人员选用不同的算法,往往会得到一组不同的“最优”飞行轨迹,如何对它们进行合理的评价进而选择出最佳飞行方案及相应的轨迹优化算法,是一个值得深入研究的问题。

近年来,飞行器制导控制领域的性能评估问题已逐渐成为新的热点[2],国内外研究多集中在制导律和控制算法的性能评估问题上,如在可重复使用飞行器、载人探索飞行器等设计验证过程中均采用一定的评估策略来确定其制导系统性能[3],为制导算法的改进与选择提供理论和数据支撑[4-5]。然而,目前对于轨迹优化算法的评估问题还处于起步阶段,至今仍没有形成公认、统一的理论方法。传统方法对飞行器轨迹的评估多采用系统仿真和蒙特卡洛随机打靶等策略,通常都是针对一种轨迹优化设计算法进行评估,没有对多种可能的优化设计展开研究[6];在轨迹优化设计相关文献中,设计算例通常局限于特定算法的比较,有失公正和客观。

针对上述高超声速飞行器再入轨迹优化算法的评估问题,本文从算法本身及其优化结果两方面建立综合评估指标体系,利用遗传算法将层次分析法的指标计算过程转化为一类优化求解问题,并综合算法数据在空间距离与曲线形状两方面与对照组的贴近度,提出一种灰色逼近理想解排序(technique for order preference similarity to ideal solution, TOPSIS)加权法,形成完整的轨迹优化算法综合评估闭环流程,为算法优选及改进提供充分的数据支撑。利用Chebyshev伪谱法与粒子群法进行实例仿真,实验结果验证了本文评估策略的有效性。

1 轨迹优化算法综合评估指标体系

再入轨迹优化算法的评估是一个典型的多目标决策问题,本文主要从算法本身特性以及对应方案轨迹的可行性、安全性、过渡性及最优性等方面进行分析,以建立全面的综合评估指标体系。

1.1 算法特性

轨迹优化算法自身的品质特性是影响其工程应用的重要因素,本文主要从稳定性(稳定度)和实时性(实时度)两方面进行量化考核。

(1)稳定度。对同一算法在考虑随机因素的情况下进行多次测试,分析其优化结果的统计特性,以协方差矩阵的迹作为衡量其稳定性的标准。文献[7]提出了一种基于正交试验设计的测试思路,本文作为设计参考,则算法稳定度计算公式为

(1)

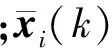
(2)实时度。对相同的轨迹优化任务,可利用平台的硬件执行速度来比较不同算法的实时性,实时度的计算公式为

(2)

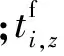
1.2 可行性

可行性是再入轨迹优化需要满足的基本条件。

(1)积分吻合度。在获得最优控制律后,可以利用数值积分近似理想开环飞行试验,通过积分轨迹与设计轨迹的偏差大小评价轨迹优化结果的控制精度,本文将该指标定义为积分吻合度,即

(3)

式中:I3(i)为算法i的积分吻合度;xi,L(k)为算法i第k时刻的积分状态向量;xi(k)为算法i第k时刻的状态向量,通常考察高度、经度及纬度等状态。

(2)控制指令平滑度。控制指令的剧烈变化会给系统造成实现上的困难,其平滑度是衡量轨迹性能的重要指标。相邻时刻控制指令的差分代表了控制指令的平滑度,其计算公式为

(4)

式中:I4(i)为算法i的控制指令平滑度;ui(k)为算法i第k时刻的控制指令向量,通常包括攻角及倾侧角。

1.3 安全性

(1)最大过载值。限于飞行器结构和弹载设备的承载能力,需对最大过载进行评估,最大过载值为

(5)

式中:ni(k)为算法i第k时刻的过载。

(2)最大动压值。动压若超过一定范围,飞行器结构会受到严重影响,需要对其进行限制,最大动压值为

(6)

式中:qi(k)为算法i第k时刻的动压。

(3)最大热流值。为了保证飞行器热防护系统正常工作,需要对最大热流密度进行评估,最大热流值为

(7)

(4)总吸热量。较小的吸热量可以有效减轻热防护系统的质量,从而提高有效载荷的设计裕量。总吸热量为

(8)

1.4 过渡性

过渡性即飞行器的初始再入点和目标终点约束,意味着再入段和前后阶段的衔接。

(1)再入点约束满足度。再入点约束通常包括飞行器位置、速度等约束,再入点约束满足度为

(9)

式中:xi,C(k)为k=1时算法i的初始状态约束向量,I9(i)为再入点约束满足度。

(2)终端约束满足度。终端约束通常包括飞行器位置、速度等状态,终端约束满足度为

I10(i)=∑|xi,C(k)-xi(k)|,k=Ki

(10)

式中:k=Ki时xi,C(k)为算法i的终端状态约束向量,I10(i)为终端约束满足度。

1.5 最优性

最优性是轨迹优化问题关注的焦点,同时也是评估轨迹优化效果的直观依据。

(1)再入飞行时间。较短的飞行时间可以降低吸热量,有效提高突防能力。再入飞行时间指标为

(11)

(2)优化目标。目标函数的最优性是判断轨迹最优性最直接的依据,同时也是判断优化算法性能的重要指标。算法i的优化目标为

(12)

1.6 层次化综合评估指标体系

本文指标体系如图1所示,包括目标层、准则层及指标层,其中准则层元素为C=(Ci),i=1,…,5,指标层元素为I=(Ii),i=1,…,12。当同时参与评估的优化算法为A={A1,A2,…,Am}时,根据评估指标集可获得原始指标数据矩阵,即原始决策矩阵

(13)

式中:bij为算法i的第j个指标值;m由使用者决定,本文中n=12。

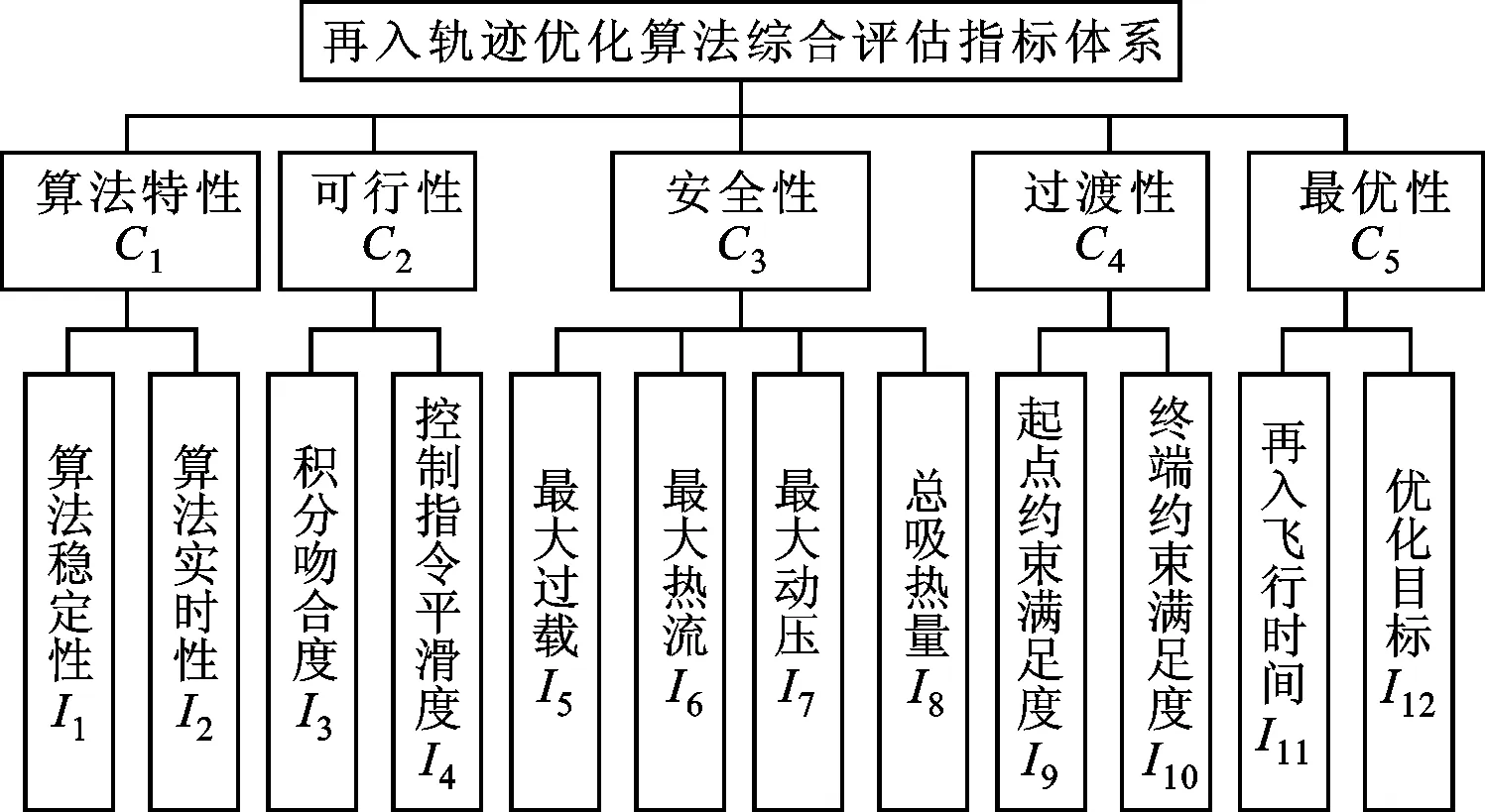
图1 层次化综合评估指标体系

为了避免指标类型与量纲差异对评估结果产生不利影响[8],同时方便决策者比较,本文通过规范化处理将式(13)原始决策矩阵映射到[0,100]区间,即

(14)

(15)

2 基于层次分析法的指标权重计算

对于多指标综合评估,需要根据指标的重要程度为其赋予相应的权重。目前,权重的确定方法主要有主观赋权法、客观赋权法及组合赋权法等[8]。考虑到高超声速飞行器的模型复杂性与数据保密性等问题,利用客观赋权法计算指标权重其合理性往往难以保证。因此,本文依据专家经验,基于层次分析法(analytic hierarchy process, AHP)[9]计算指标权重,并利用遗传算法改进其权重计算过程。

以AHP法中建立的两两比较判断矩阵为依据,综合考虑最小欧氏距离与最少违例准则,可将指标权重的计算问题转化为一类多目标优化问题[10]。

设S={aij|j>i}为判断矩阵的上三角阵元素,指标权重向量ω=[ω1,…,ωn]T的可行解集Q可表示为

(16)

利用权重比值与判断矩阵上三角阵对应元素的欧氏距离来衡量权重向量的近似精度,即

(17)

另一方面,为了保证权重优先级与判断矩阵信息保持一致,采用最少违例准则对权重进行约束

(18)

式中

(19)

权衡2种衡量标准,给定相应的权重系数,可将该多目标优化问题变换为单目标优化问题,即

(20)

式中:系数α∈[0,1],本文中α取为0.5。

采用遗传算法求解式(20),即可获得评估所需要的指标权重向量。通过权重逐层相乘,最终获得底层指标对于评估目标的重要性排序,即综合权重

(21)

3 灰色TOPSIS加权算法

3.1 加权规范化决策矩阵

利用式(15)规范化决策矩阵与式(21)底层指标综合权重,即可构造评估所需要的加权规范化决策矩阵

(22)

在此基础上,基于AHP法的评估可直接给出算法i的综合评估值

(23)

AHP评估结果仅基于指标数值与对应权重的乘积求和,它并未从全局角度进行考察,只能得到优化算法的抽象排序,无法说明再入轨迹的整体特征。针对这一不足,本节在式(22)加权规范化决策矩阵基础上展开讨论,综合TOPSIS法[11]与灰色关联分析(grey relational analysis, GRA)法[12]这2种算法的特点,提出了一种综合排序方法。

3.2 灰色TOPSIS加权法

TOPSIS是一种逼近理想解的排序方法,依据被评估方案与正、负理想方案在空间距离上的远近进行排序,TOPSIS一个明显的缺点在于:当备选解与理想点欧氏距离更近时,可能与负理想点的欧氏距离也更近[13]。GRA基于灰色关联度,侧重分析数据序列的几何关系和曲线形状,将曲线之间的相似程度大小作为数据序列关联程度的衡量标准。

本文综合被评估方案在空间距离与曲线形状上与理想方案的贴近度,提出一种新的多目标决策方法——灰色TOPSIS加权法(weighted grey TOPSIS, WGT),计算步骤如下。

(24)

(25)

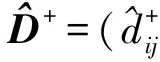
(5)计算加权复合偏差矩阵

式中:γ∈(0,1)为加权系数,由设计者决定,体现了决策者对2种算法的偏好,本文取γ=0.5。

(6)计算各算法方案与正负理想解的综合偏差

(28)

(29)

(7)计算各算法方案的综合相对贴近度

(30)

(8)根据相对贴近度Ti对优化算法进行排序,Ti越大对应的优化算法性能越好,反之则越差。

WGT法从相对贴近度的构造角度对TOPSIS法进行了改进,在一定程度上弥补了TOPSIS法本身的不足。此外,由于评估指标的绝对正理想解与绝对负理想解不会受到参评数据的影响而产生变化,避免了逆序现象,从而降低了不确定性。

3.3 优化算法综合评估策略

本文综合评估策略的原理流程如图2所示,包括再入轨迹优化、飞行仿真验证、评估指标提取和算法性能评估4部分,形成了完整的闭环评估过程,具有良好的封装性与通用性,评估输出结果可以对不同的轨迹优化算法进行综合评价,同时也能为优化算法自身的改进提供量化反馈信息。

4 仿真分析

为了验证本文综合评估策略的有效性,以Chebyshev伪谱法(Chebyshev pseudospectral method, CPM)[14]与粒子群法(particle swarm optimization,PSO)[15]为对象,在通用航空飞行器[16]三自由度动力学模型基础上进行再入轨迹优化实例仿真与评估分析。

4.1 仿真实验条件

仿真平台采用2.33 GB主频CPU、2 GB内存的PC机,软件环境为Matlab 2009。以再入飞行时间最短为轨迹优化目标;初始状态为高度100 km,速度7 200 m/s,经度160°,纬度25°,航迹角-2°,航向角58°;终端状态约束为高度20 km,经度232°,纬度37°,速度1 km/s;过程约束中最大热流密度为1 MW/m2,最大动压为400 kPa,最大过载为6。

为了简化计算过程,根据1.1节关于稳定性的描述,以CPM与PSO分别产生5组弹道数据为例进行统计分析,以弹道数据协方差的迹作为稳定性指标数据,以均值作为算法典型轨迹数据。经计算,2种算法的典型方案轨迹如图3所示。

4.2 指标数据提取

获得方案数据后,根据1.6节建立的评估指标数学模型进行计算处理,获得的CPM与PSO算法评估指标数据如表1所示。需要指出,本例中优化目标与最短飞行时间指标为同一指标。

4.3 指标权重计算

在AHP判断矩阵基础上基于遗传算法计算指标权重,采用10位二进制编码,种群数为500,迭代次数为200, 交叉概率为0.65, 变异概率为0.1,用轮盘算法进行选择操作。指标层元素对于评估目标的综合权重通过指标层权重与对应准则层权重相乘获得。

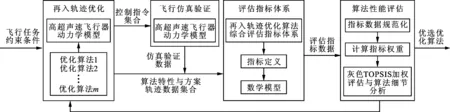
图2 轨迹优化算法综合评估策略流程图

算法I1I2/sI3I4I5I6/kW·m-2I7/kPaI8/MJI9I10I11/sCPM43251275505239472539699138993133045421487PSO75401352396785261551544337483266034981485

图3 CPM与PSO算法再入方案轨迹3D图

本例中指标I11与I12相同,最终指标层元素综合权重向量为

ω=[0.091 9,0.046 0,0.165 9,0.110 0,

0.044 4,0.060 4,0.076 5,0.060 2,

0.068 9,0.068 9,0.206 9]T

4.4 评估结果分析

利用式(14)对表1中的评估指标数据进行归一化处理,并分别采用TOPSIS、GRA与本文提出的WGP方法对算例进行评估,结果如表2所示,评分越高算法性能越好,排序越靠前。

表2 轨迹优化算法综合评分结果

从表2可看出:3种算法给出的评估结果中,CPM算法的综合性能评分均高于PSO算法;本文WGT方法与TOPSIS及GRA方法的评估结论保持了良好的一致性,说明本文WGT方法是合理的,能够对不同优化算法进行综合排序;由于WGT方法对TOPSIS与GRA进行了融合,考察内容同时包含了算法数据在曲线形状及空间距离上与理想最优解的差距信息,评估角度更加全面,评估得分更为合理。

WGT方法步骤中式(27)为加权复合偏差矩阵,代表了被评估算法与负理想组的空间偏差以及与正理想组的关联程度,其元素值越大说明评估指标与负理想组距离越远且与正理想组关联越强,亦即性能越好。分析其矩阵数据,可获得符合常规评估习惯的算法细节信息,为算法的改进提供事实依据。本例中WGT方法的加权复合偏差矩阵折线图如图4所示。

从图4可以看出,2种优化算法的表现各有千秋。在算法稳定性I1与实时性I2方面,PSO算法明显落后于CPM算法,分析原因在于PSO算法是一种全局性的随机搜索算法,需要大量的数据样本和迭代计算,而CPM将问题转化为参数的非线性规划问题,并基于梯度信息寻优,求解效率更高。随着弹载计算机硬件执行速度的提升,加之以算法改进和代码优化等措施,CPM更有望发展成为一种在线轨迹优化求解算法。

图4 本文WGT方法加权复合偏差折线图

CPM算法的积分吻合度指标I3不如PSO算法,原因在于CPM算法只在离散的配点处满足动力学方程约束,而PSO算法在求解过程中将节点处的控制变量代入动力学方程并通过数值积分获得状态量,一定程度上使其满足了积分轨迹与优化轨迹的一致性。另一方面,CPM获得的控制律平滑度I4明显优于PSO算法,更易于工程实现,这得益于CPM优化算法在控制量变化率约束计算上的精度控制。

此外,由于均以起点状态为求解基础,2种算法的起点状态偏差I9均得到了严格控制;CPM的终端状态偏差I10虽略大于PSO,但仍在制导控制系统可调整范围内。在最优性方面,CPM与PSO算法获得的最短再入飞行时间相差无几,说明对于高超声速飞行器最短再入时间轨迹优化问题,2种算法均具有良好的寻优性能。

综合来看,CPM算法总体性能表现更出色,但其在可行性与过程约束控制上仍有改进的空间,而PSO算法的实时性是制约其实际应用的最大瓶颈,当不考虑求解效率时,仍不失为一种有效的轨迹优化算法。

5 结 论

针对高超声速再入飞行器轨迹优化算法优选的工程问题,建立了一套兼顾优化算法特性和飞行轨迹质量的评估指标体系,利用遗传算法与AHP法计算指标权重,提出了一种灰色TOPSIS加权排序法,建立了完整的再入轨迹优化—飞行仿真验证—算法性能评估闭环设计流程。对CPM算法和PSO算法的仿真实验表明,本文评估策略实现了算法性能的量化过程,指标体系和评估方法科学有效,能够为决策者快速遴选出适合任务需求的最优算法,同时也为被评估算法的改进提供了具体的数据参考。

[1] ZHAO J, ZHOU R, JIN X. Progress in reentry trajectory planning for hypersonic vehicle [J]. Journal of Systems Engineering and Electronics, 2014, 25(4): 627-639.

[2] TANCREDI U, GRASSI M, CORRARO F, et al. Robustness analysis for terminal phases of reentry flight [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(5): 1679-1683.

[3] HANSON J, JONES R, KRUPP D. Advanced guidance and control methods for reusable launch vehicles: test results [C]∥Proceedings of AIAA Guidance Navigation and Control Conference. Reston, VA, USA: AIAA, 2002: 4561-4569.

[4] BRUNNER C W, LU P. Comparison of fully numerical predictor-corrector and Apollo skip entry guidance algorithms [J]. The Journal of the Astronautical Sciences, 2012, 59(3): 517-540.

[5] 马卫华. 高超声速飞行器制导与控制性能评估方法 [J]. 航天控制, 2012, 30(4): 7-12. MA Weihua. Research on evaluation method of guidance and control performance for hypersonic vehicle [J]. Aerospace Control, 2012, 30(4): 7-12.

[6] RINAT K, BEN-ASHER J Z. Worst-case distributions for performance evaluation of proportionally guided missiles [J]. Journal of Guidance, Control, and Dynamics, 2000, 23(5): 895-898.

[7] 董春云, 蔡远利. 基于正交试验设计的弹道优化算法评估研究 [C]∥第32届中国控制会议论文集. 北京: 中国自动化学会控制理论专业委员会, 2013: 8542-8545. DONG Chunyun, CAI Yuanli. Orthogonal design based evaluation for trajectory optimization algorithms [C]∥The 32nd Chinese Control Conference. Beijing: Technical Committee on Control Theory, Chinese Association of Automation, 2013: 8542-8545.

[8] 张杰, 唐宏, 苏凯, 等. 效能评估方法研究 [M]. 北京: 国防工业出版社, 2009: 8-26.

[9] SAATY T L. Decision making with the analytic hierarchy process [J]. International Journal of Services Sciences, 2008, 1(1): 83-98.

[10]SIRAJ S, MIKHAILOV L, KEANE J A. Preference elicitation from inconsistent judgments using multi-objective optimization [J]. European Journal of Operational Research, 2012, 220(2): 461-471.

[11]OLSON D L. Comparison of weights in TOPSIS models [J]. Mathematical and Computer Modelling, 2004, 40(7): 721-727.

[12]WU H H. A comparative study of using grey relational analysis in multiple attribute decision making problems [J]. Quality Engineering, 2002, 15(2): 209-217.

[13]华小义, 谭景信. 基于“垂面”距离的TOPSIS法: 正交投影法 [J]. 系统工程理论与实践, 2004, 24(1): 114-119. HUA Xiaoyi, TAN Jingxin. Revised TOPSIS method based on vertical projection distance: vertical projection method [J]. Systems Engineering: Theory & Practice, 2004, 24(1): 114-119.

[14]FAHROO F, ROSS I M. Direct trajectory optimization by a Chebyshev pseudospectral method [J]. Journal of Guidance, Control, and Dynamics, 2002, 25(1): 160-166.

[15]RAHIMI A, DEV KUMAR K, ALIGHANBARI H. Particle swarm optimization applied to spacecraft reentry trajectory [J]. Journal of Guidance, Control, and Dynamics, 2012, 36(1): 307-310.

[16]PHILLIPS T H. A common aero vehicle model, description and employment guide [R]. New York, USA: Schafer Corporation for AFRL and AFSPC, 2003.

(编辑 刘杨)

An Evaluation Strategy of Trajectory Optimization Algorithms for Hypersonic Reentry Vehicle

DONG Chunyun,CAI Yuanli

(School of Electronic and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

A comprehensive evaluation strategy is proposed to deal with the evaluation of various trajectory optimization algorithms for the hypersonic reentry vehicle. An integrated index system is established by taking the stability and real-time performance of each algorithm itself as well as the feasibility, security, transitivity and optimality of its optimization result into account. And the calculation of index weights is transformed into an optimization problem based on the pairwise judgement matrix of the analytic hierarchy process, and the Euclidean distance and the number of violations are used as precision measures. The genetic algorithm is used to solve the optimization problem. Then, the normalized decision matrix is obtained, and a weighted grey technique for order preference by similarity to ideal solution (TOPSIS) is proposed by synthesizing the nearness degree in both the space and curve between the algorithm data and the ideal control groups to achieve the final evaluation results. Simulation results show that the proposed strategy uses objective data to quantify the performance of trajectory optimization algorithms, and forms a comparative evaluation standard for various algorithms. The strategy can help designers quickly select an optimal algorithm according to different mission requirements and avoid blindness and subjectivity.

hypersonic reentry; trajectory optimization; algorithm evaluation

2015-08-08。 作者简介:董春云(1989—),女,博士生;蔡远利(通信作者),男,教授,博士生导师。 基金项目:国家自然科学基金资助项目(61463029,61308120,61202128);宇航动力学国家重点实验室开放基金资助项目(2011ADL-JD0202)。

时间:2016-01-13

10.7652/xjtuxb201604005

TP29

A

0253-987X(2016)04-0028-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160113.2000.012.html