铣刨机旋转多刀铣削阻力的数值计算

汪学斌,胡永彪

(长安大学道路施工技术与装备教育部重点实验室,710064,西安)



铣刨机旋转多刀铣削阻力的数值计算

汪学斌,胡永彪

(长安大学道路施工技术与装备教育部重点实验室,710064,西安)

为计算沥青路面冷铣刨机的旋转多刀铣削阻力,将单把刀具旋转变厚度铣削的任一瞬时近似为等厚度平移切削,平移速度为刀具刀尖点轨迹的切线速度,以剪切破坏建立了单刀铣削阻力计算模型;将任一时刻各刀具铣削阻力的向量叠加作为该时刻铣削转子的旋转多刀铣削阻力,得到了旋转多刀铣削阻力切向分力的数值计算方法。结合试验数据,以铣削接触面截面积为自变量修正了单刀铣削阻力计算公式,并对比了冷铣刨机试验样机旋转多刀铣削阻力切向分力的实测值与理论计算值,结果表明二者线性相关,相关系数R2=0.9;进而修正了旋转多刀铣削阻力切向分力的计算公式,分析了理论计算值的误差来源。所提出的单刀铣削阻力和多刀铣削阻力计算模型可为旋转类多刀具切削阻力数值计算提供参考。

沥青路面铣刨机;铣削阻力;多刀铣削;数值计算

铣刨是现代沥青路面破除的主要方式,是按一定规律排布多把子弹头型铣刀的铣削转子在旋转过程中各刀具逐次切入和切出,使被铣削路面材料在刀具的高速冲击挤压下产生变形破坏而被切除。针对沥青路面铣削阻力的计算问题,文献[1-2]中借鉴了金属切削理论,但将多刀旋转铣削过程看成是等同铣削宽度和深度的楔形刀具平移切削,忽视了刀具逐次切入切出的过程及刀具的动态冲击作用。将多刀旋转渐进铣削简单平移化与实际的铣削过程并不相符。文献[3-4]中铣削阻力的计算需要通过试验确定切削比阻,而文中主要采用的是试取值。沥青路面冷铣刨机滚筒上各刀具的运动轨迹为水平方向上的进给运动和圆周运动的合成,旋转多刀铣削阻力是瞬时同时参与铣削的各刀具铣削阻力的向量叠加。单刀铣削阻力计算是沥青路面冷铣刨机多刀铣削阻力研究的基础,铣削转子直径、铣削作业速度、转子转速、铣削宽度、铣削深度和刀具排布参数决定了各刀具实时铣削状态及同时参与铣削的刀具数目,进而决定了任意瞬时多刀具联合作用下的铣削阻力和铣削阻力矩。本文将在分析刀具冲击挤压下沥青混凝土铣削变形破坏过程的基础上,建立单刀和旋转多刀铣削阻力数值计算模型,参考试验数据进行单刀铣削阻力计算公式和旋转多刀铣削阻力切向分力理论计算公式的修正,并对旋转多刀铣削阻力数值计算的误差来源进行分析。

1 单刀具铣削阻力计算模型

沥青混凝土主要是由沥青胶结料与一定粒径分布的集料经搅拌、摊铺、压实形成的具有一定孔隙的路面结构层。常温铣削状态下沥青混凝土是非均质各向异性的弹、塑、脆性材料[5],温度越低其脆性越显著,且沥青混凝土中的矿质集料属脆性材料。铣削时刀具以一定角度和速度锲入沥青混凝土,刀具前刀面的沥青混凝土受到冲击挤压而产生变形破坏,由于沥青的黏结强度比集料的破坏强度小,铣削过程主要是沥青混凝土沿黏结面的剥离并伴随少量集料的破碎,主要为剪切破坏[6-7]。

单刀铣削作业过程与铣削厚度变化如图1所示。以铣刨转子滚筒中心O点为原点建立坐标系(这里只讨论周向截面刀具数量为1的铣削转子),R为刀尖圆半径,ω为铣削转子旋转角速度,v为铣削作业速度,φ为铣削转子实时转角,δ为刀具铣削作用角(δ=φe-φs),φs为刀具切入角,φe为切出角,θ为剪切角,d为铣削深度,h为实时铣削厚度,l为铣屑长度,F为刀具所受铣削阻力,Fm为单刀沿铣削轨迹切线方向的铣削阻力切向分力,Fn为铣削阻力法向分力,φ为F与Fm的夹角,β为铣削阻力F与铣削水平分力Fx的夹角,Fy为铣削阻力竖直分力。铣刨机采用的子弹头型铣刨刀具可简化为刀尖角为κ的圆锥形刀具,且可以用点作用力代表整个刀具的受力[8]。刀具刀尖顶部与沥青混凝土近似为球形接触,以刀尖顶点A的运动轨迹表示刀尖点的铣削轨迹,A点的线速度vL=ωR,A点轨迹的切线速度为A点进给速度v和线速度vL的合速度vT。刀尖由A″点切入,当刀尖在铣削轨迹A″E上的A点时,刀尖点A的瞬时铣削厚度t即为AA′,A′点为刀尖点A的前一铣削循环轨迹线与曲率半径O′A的交点,当铣削转子转角为φ时,A点的坐标为(vφ/ω+Rsinφ,-Rcosφ)。铣削厚度tAA′=[(xA-xA′)2+(yA-yA′)2]1/2;刀尖越过E点后,铣削厚度tFF′=[(xF-xF′)2+(yF-yF′)2]1/2;tEE′为最大铣削厚度。铣削厚度值由R、v、φ、ω确定,采用MATLAB编程可求得任意精度的铣削厚度值。

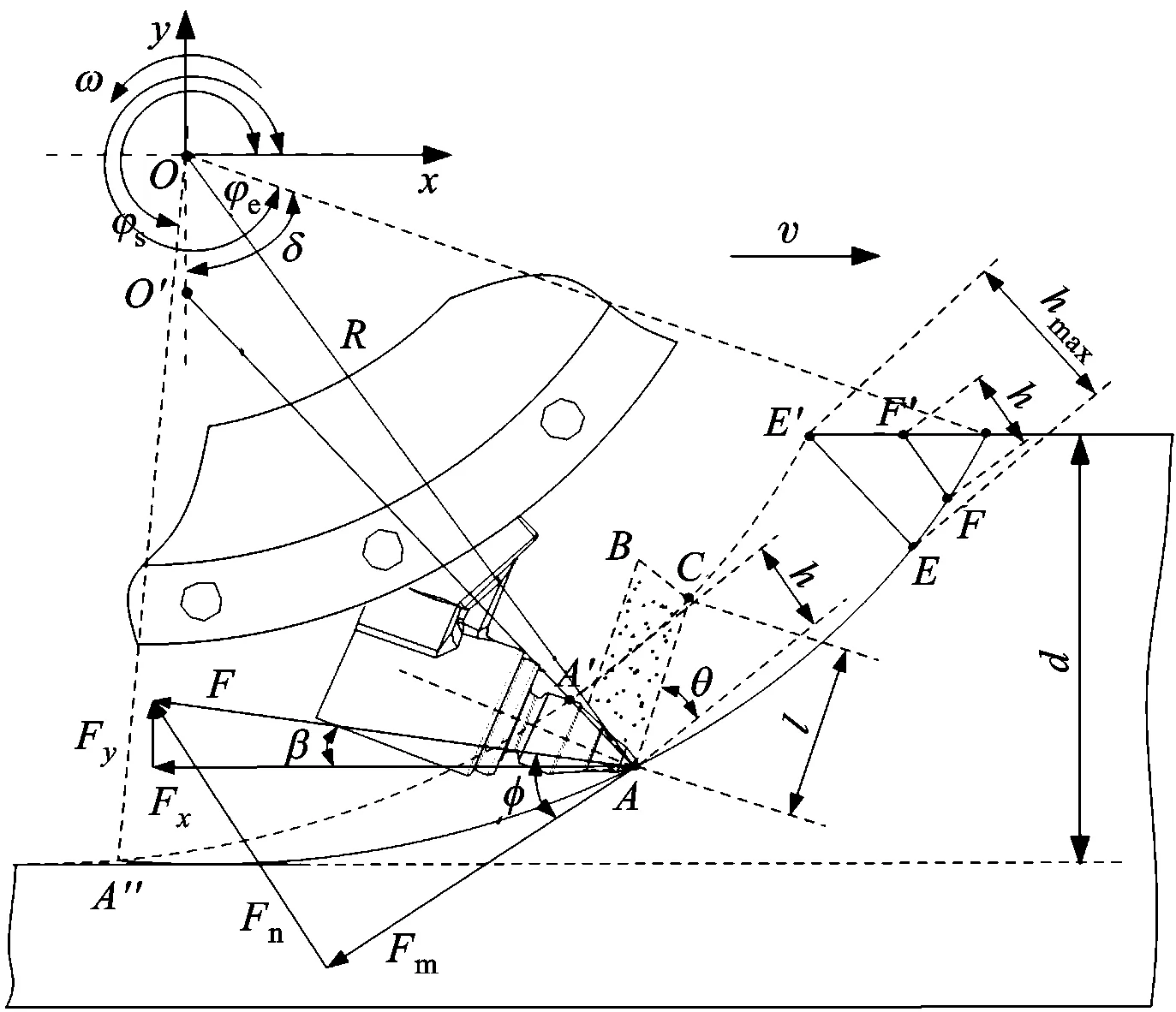
图1 单刀铣削作业过程与铣削厚度变化示意图

单把刀具在完成一个铣削循环后,与其相邻的刀具也将完成一次铣削动作。设刀具间距为a,考虑相邻刀具间的相互作用,单把刀具与被铣削材料接触面的截面积S具有下述特征:当铣削厚度小于0.5acot(κ/2)时,接触面截面近似为三角形,三角形的高等于铣削厚度;当铣削厚度大于0.5acot(κ/2)时,由于相邻刀具的相互作用,三角形上部的截面积可近似为矩形,如图2所示。

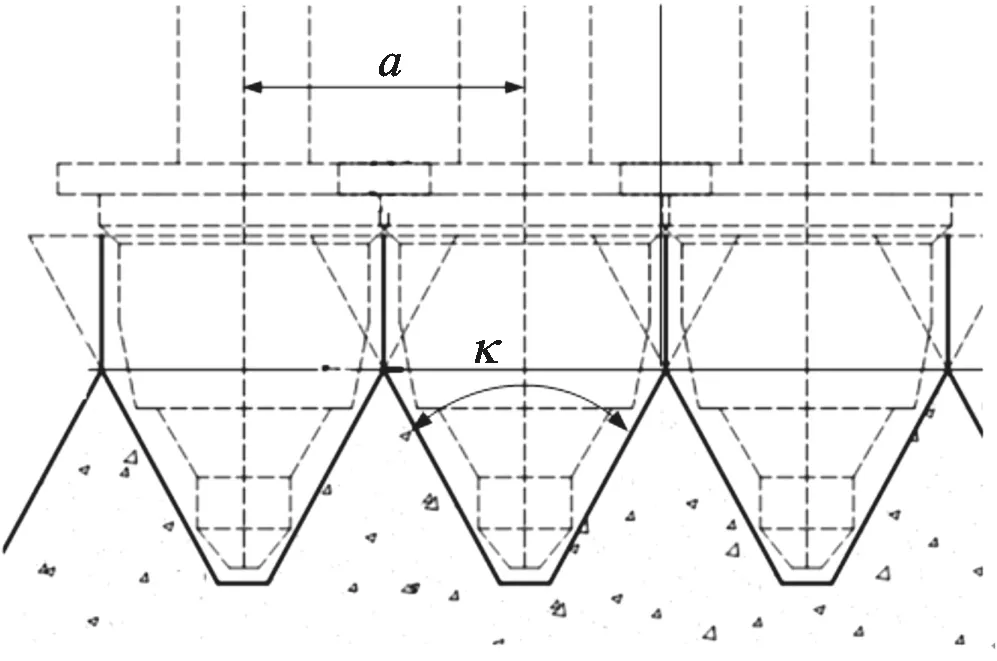
图2 相邻各刀具与被铣削材料接触面积计算示意图

S的计算公式为

(1)

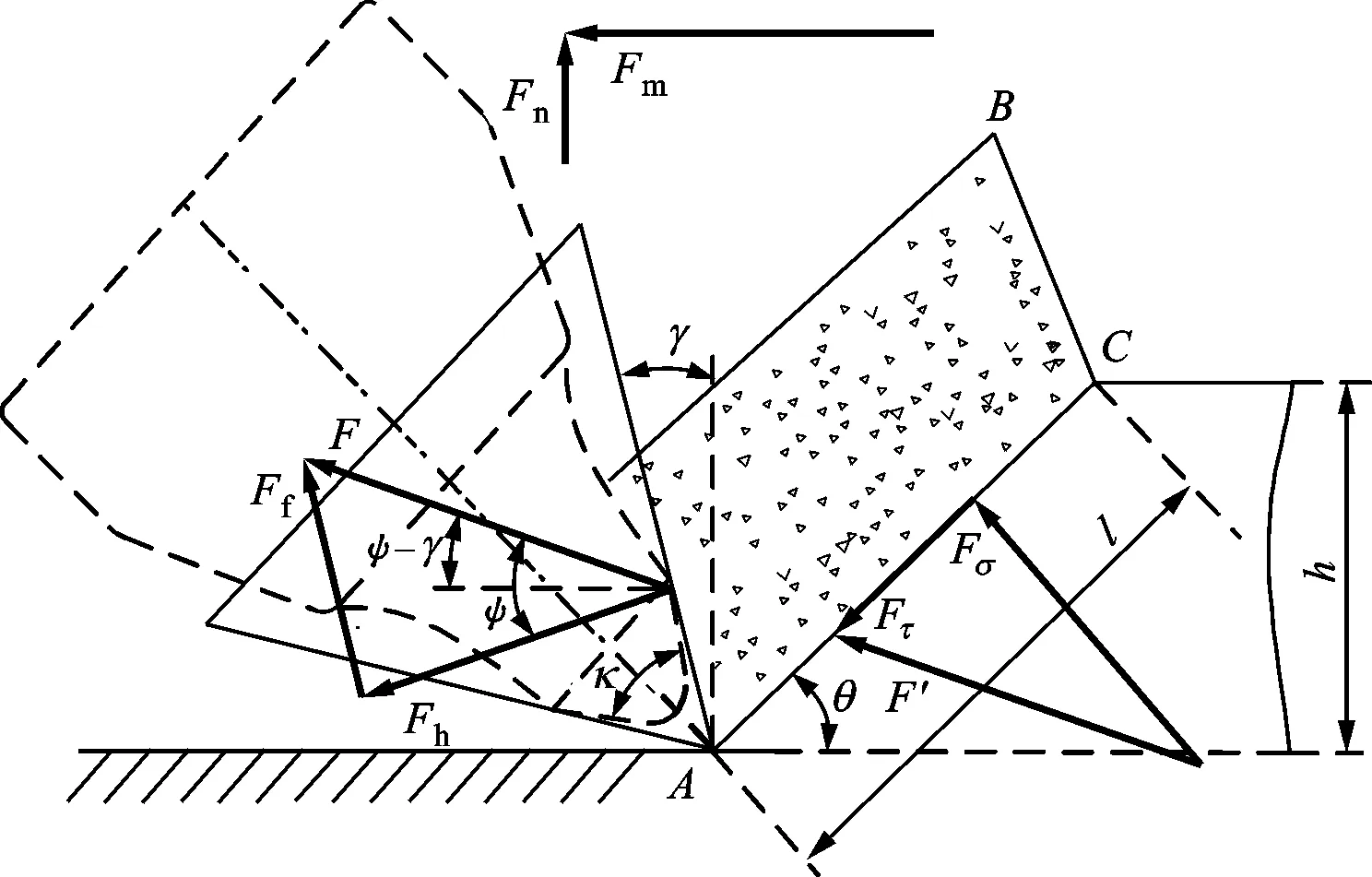
图3 单刀旋转铣削过程的瞬时受力模型

单刀旋转变厚度铣削在任意瞬时可近似为等厚度平移切削,平移速度为刀具刀尖点轨迹的切线速度vT,铣削厚度和接触面截面积随铣削过程不断变化。单刀旋转铣削沥青混凝土的瞬时受力模型如图3所示,与刀具前刀面接触的沥青混凝土受到冲击挤压后沿剪切面AC断裂[9-11]。忽略铣削废料的重力,作用在剪切面上的正压力为Fσ,剪切力为Fτ,合力为F′;前刀面的法向压力为Fh,摩擦力为Ff,二者的合力即为刀具所受的铣削阻力F,F和F′相等;铣削阻力F可分解为铣削阻力切向分力Fm和铣削阻力法向分力Fn,Fn垂直于铣削转子中心,不消耗铣削功率;ψ是F和Fh的夹角,即刀具前刀面与铣削阻力的夹角,又称摩擦角;γ为刀具铣削前角,φ=ψ-γ,β=φ-φ。

(2)

式中:As为剪切面积,即S沿剪切面的投影,As=S/sinθ。

(3)

剪切破坏发生在沿变形阻力最小的方向,即

所以,当cosθcos(θ+ψ-γ)-sinθsin(θ+ψ-γ)=0,即cos(2θ+ψ-γ)=0、剪切角θ=π/4-(ψ-γ)/2时,可使铣削阻力F取最小值[12]。单刀铣削阻力的切向分力和法向分力分别为

(4)

(5)

铣削阻力的水平分力和竖直分力分别为

(6)

(7)

以上各式中:τ为沥青混凝土的剪切强度。铣削前角γ由刀具的安装角确定,并随转子转角而变化,γ=γ0-ϑ,其中γ0为刀尖点A在轨迹最低点时的切削前角,亦即初始切削前角,ϑ为刀尖点的线速度vL与刀尖点轨迹的切线速度vT的夹角,由下式计算

(8)

2 多刀铣削阻力计算模型

图4 典型铣削转子的结构及作业过程示意图(未包含边刀和侧刀)

典型的铣削转子刀具布置如图4所示。随铣削转子的转动,滚筒上的各刀具逐次切入沥青混凝土,而后逐次切出路面,各刀具均经历相同的铣削过程。在任一时刻,同时参与铣削的各刀具处于不同的铣削深度和铣削轨迹线上,对应不同转角和铣削厚度,如图5所示。铣削转子旋转多刀铣削的阻力为同时参与铣削各刀具铣削阻力的向量叠加,多刀铣削阻力可以看成是一个大的直流分量与一个小幅值交流分量的叠加。

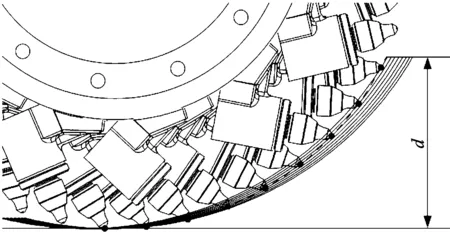
图5 任一时刻同时参与铣削的各刀具的铣削状态

主刀总数记为N(因侧刀主要产生轴向力,边刀刀间距相对主刀刀间距较小,且周向截面边刀数较多,边刀每一铣削循环铣削阻力较小,只记主刀的铣削阻力对铣削转子总铣削阻力的计算影响较小,也简化了计算),铣削转子下至规定铣削深度后,任一时刻ti各刀具的转角

φij=ωti+2π(j-1)/N,j=1,2,…,N

(9)

各刀具刀尖点的坐标为

(vφij+Rsinφij,-Rcosφij),j=1,2,…,N

(10)

在任一时刻ti,刀具转角在2πn+φs<φij<2πn+φe(n=0,1,2,…)范围内各刀具的铣削阻力切向分力之和即为旋转多刀铣削阻力的切向分力;当刀具转角在切入角和切出角之外时,其铣削厚度和铣削阻力为0。任一时刻多刀铣削阻力的水平(x向)分力和竖直(y向)分力为

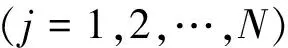
(11)

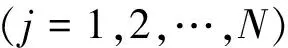
(12)

当各刀具铣削阻力的x、y向分力向多刀铣削阻力合力的作用点平移时,平移力偶相互抵消。任一时刻旋转多刀铣削阻力为

∑F=((∑Fxi)2+(∑Fyi)2)1/2=

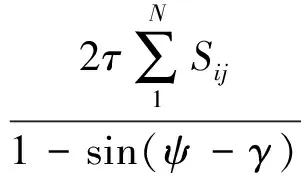
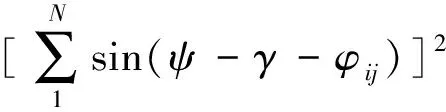
(13)

∑Fxi与∑F的夹角

(14)

多刀铣削阻力合力的作用点对应的转角(方向角)φ=ψ-γ-β,沿作用点切线方向的分力即为多刀铣削阻力切向分力。作用点到铣削最低点的纵向距离w=R(1-cosφ)。多刀铣削阻力的切向分力

(15)

3 单刀铣削阻力计算公式的修正

为验证单刀铣削阻力的理论计算公式,对铣削作业速度、铣削转子直径和转速取不同数值进行铣削阻力的理论计算,并与试验结果[13]进行比较。采用某市政道路用AC-20沥青混凝土,剪切强度τ=1.6 MPa;刀具简化后的刀尖角κ=75°,刀具与混凝土的摩擦角ψ=31°,初始切削前角γ0结合刀具安装角(安装角取45°)及简化模型取5.5°,刀间距a=15 mm,铣削转子的旋转角速度ω=2πn/60,其中n为铣削转子转速。单把刀具由于其边界条件限制(非多刀具共同作用),不能实现大深度铣削,故取d=25 mm。单刀铣削厚度和铣削阻力的理论计算采用MATLAB程序实现,单刀铣削阻力切向分力的实测值由安装于转子驱动轴上的扭矩传感器检测数据换算得出。计算结果表明:单刀铣削阻力切向分力的计算值随铣削转子转角的变化特征与实测值一致;单刀铣削循环中的铣削阻力峰值在最大铣削厚度处;用铣削阻力峰值和实测值峰值进行误差分析与模型修正是可行的。刀具与被铣削材料接触面的截面积S可表征实时刀具接触面积、铣削作业速度、铣削转子直径和转速对单刀铣削阻力的影响,因此以S为自变量进行单刀铣削阻力切向分力计算公式的修正,修正的过程数据见表1。

单刀铣削阻力切向分力的修正系数k=29.42S-0.67,修正系数计算曲线如图6所示,相关系数为0.988。修正后单刀铣削阻力切向分力的计算公式为

(16)

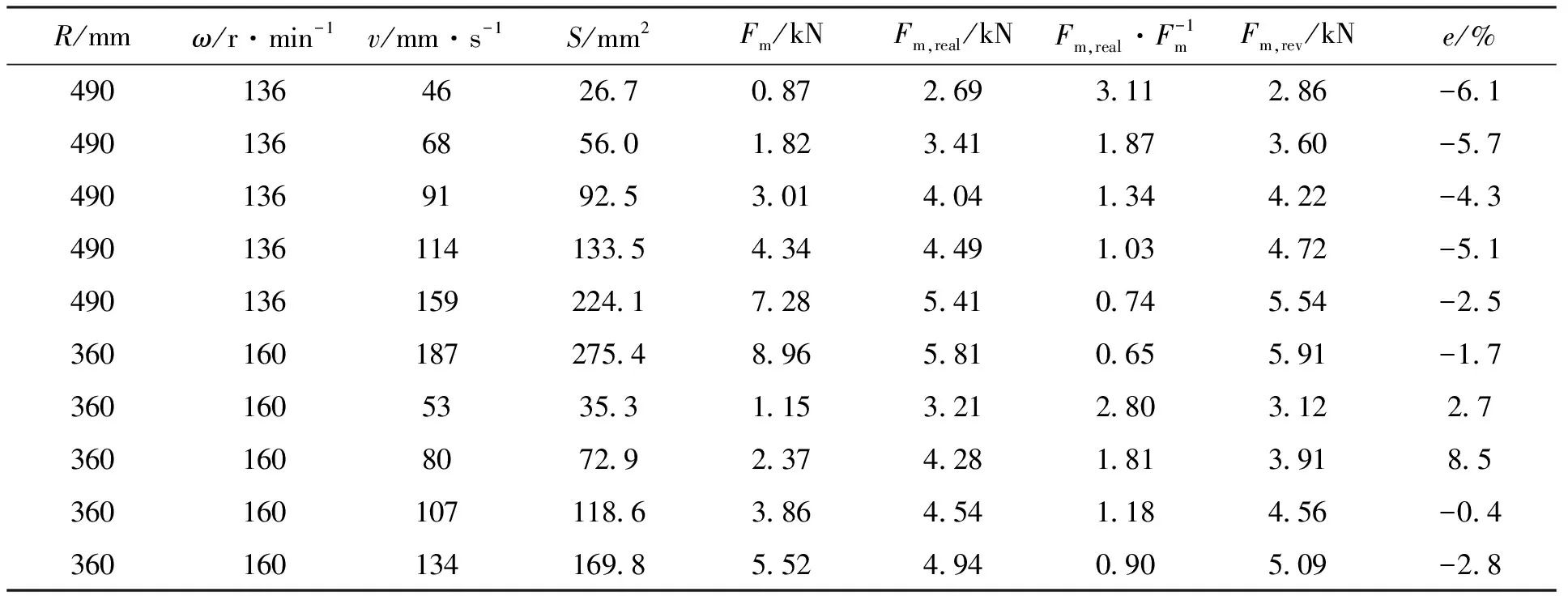
Fm,real:单刀铣削阻力切向分力实测值;Fm,rev:修正后的单刀铣削阻力切向分力计算值;e:Fm,rev与Fm,real的相对误差。

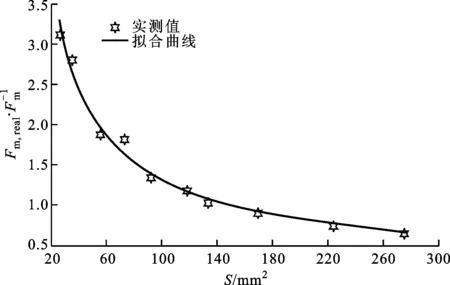
图6 单刀铣削阻力切向分力计算公式修正曲线

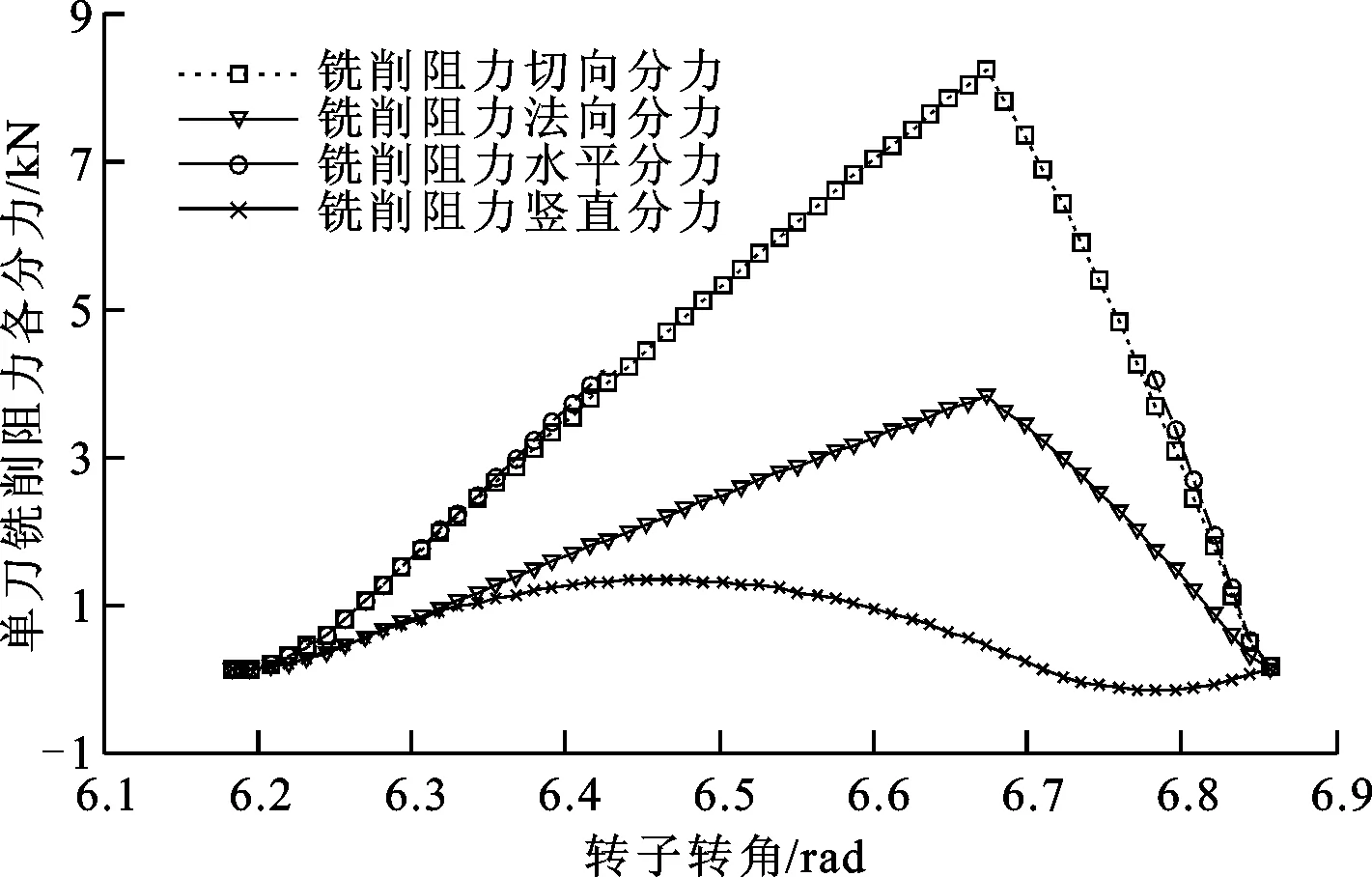
图7 单刀铣削阻力各分力随转子转角的变化

取R=490 mm,vT=6 m/s,v=200 mm/s,d=80 mm,修正后单刀铣削阻力的水平分力、竖直分力、切向分力和法向分力随转子转角的变化过程如图7所示(图中铣削转子转角从刀具旋转第二周开始计)。在刀具未达到最低点(图7中最低点转角为2π)时刀具已切入,切入后铣削厚度和铣削阻力切向分力均随转子转角的增大而增大,至最大铣削厚度处达到最大,而后减小,随后切出路面,单刀一个旋转周期只有部分时间(作用角δ范围内)在切削,其余时间铣削阻力为0。

4 旋转多刀铣削阻力数值计算及修正

为验证上述多刀铣削阻力计算方法的可行性,采用某铣刨机在不同工况下多刀铣削阻力切向分力和驱动扭矩的实测数据[4,14]与多刀铣削阻力切向分力的理论计算值进行对比。该样机的铣削宽度为1 000 mm,刀尖圆半径R=430 mm,主刀数N=60,刀间距a=15 mm,发动机额定转速时的铣削转子转速n=130 r/min。当取R=430 mm、n=130 r/min、v=10 m/min、d=100 mm时,旋转多刀铣削阻力的计算过程如图8、图9所示。

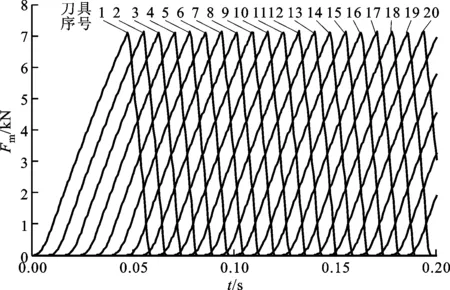
图8 各刀具铣削阻力切向分力计算值随时间的变化

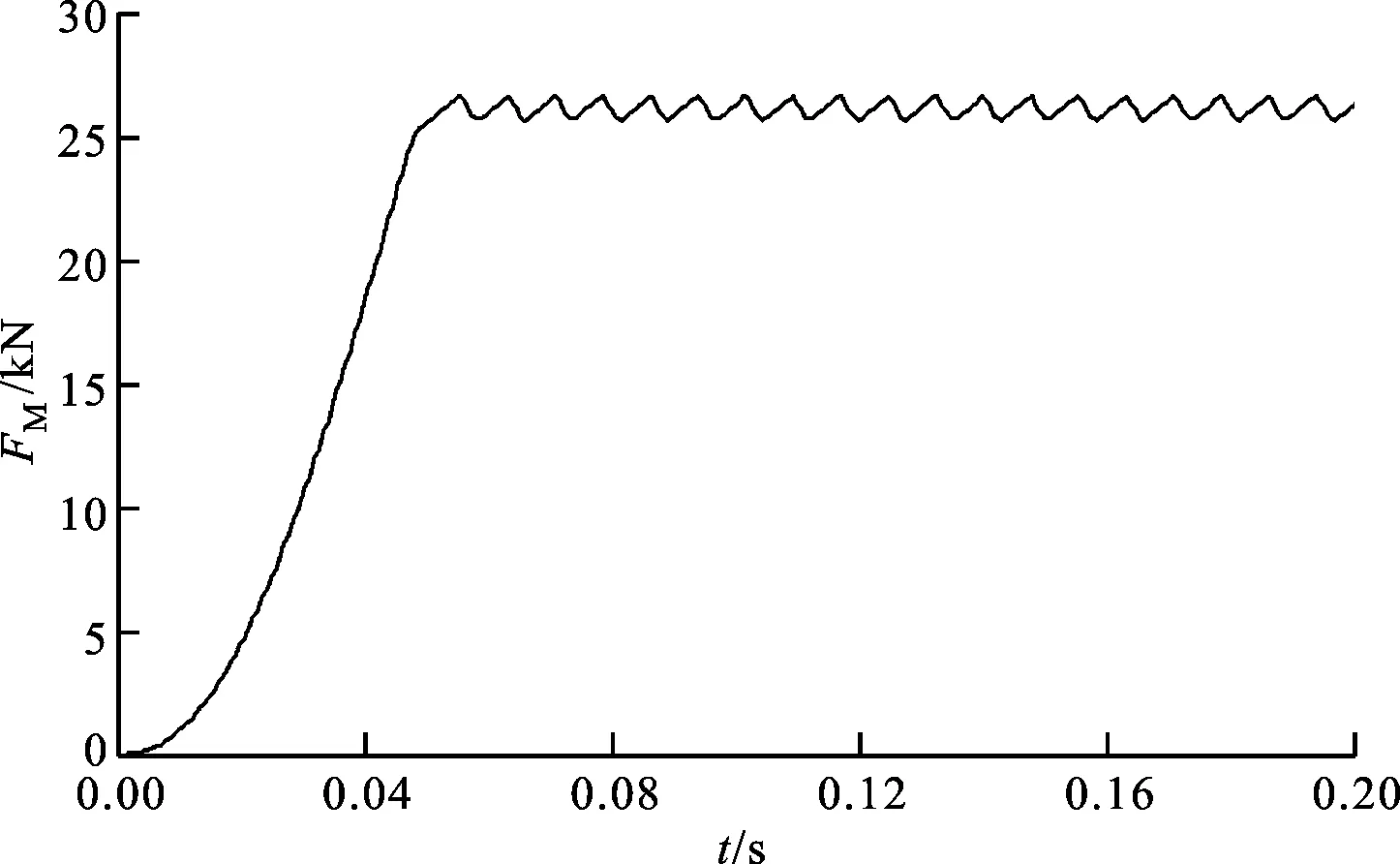
图9 多刀铣削阻力切向分力计算值随时间的变化

从刀具1切入开始计,随铣削转子旋转,刀具2、3、4……逐次切入,各刀具的铣削厚度和铣削阻力切向分力均从0增至最大,而后减小为0切出路面,至0.05 s时进入稳定铣削状态,同时参与铣削的刀具数量保持稳定,如图8所示。0～0.2 s内任一时刻旋转多刀铣削阻力切向分力的计算结果如图9所示,0.05 s之后多刀铣削阻力计算值的波动主要是由于任一时刻参与铣削的刀具数量和各刀具铣削阻力切向分力有所不同所致。

样机铣削转子的驱动采用定量泵-定量马达闭式系统,液压泵排量为250 mL/r,液压马达排量为1 000 mL/r。在不同工况下,对驱动马达高低压腔的压力、铣刨机两侧立柱高低压腔的压力、转子转速、发动机转速等参数进行检测,结果均取平稳工作一段时间的平均值。多刀铣削驱动扭矩Mreal等于铣削作业时的驱动扭矩M1减去空转时的驱动扭矩M2,即

(17)

多刀铣削阻力切向分力实测值由下式计算

(18)

式中:Δpm1为铣刨机铣削沥青混凝土时转子驱动马达高低压腔的压力差,MPa;Δpm2为铣刨机铣削转子空转时驱动马达高低压腔的压力差,MPa;qm为铣削转子驱动马达的排量,mL/r;η为液压系统的传动效率,随压力和转速而变化,取η=0.7。

让样机在不同工况(铣削深度和铣削作业速度的不同组合)下进行铣削作业,测量铣削转子驱动扭矩的平均值。铣削深度分别取30、90、150和190 mm,铣削作业速度分别取5、10、15和20 m/min,计算旋转多刀铣削阻力切向分力,并将计算结果与实测值列于表2进行比较。

铣削转子多刀铣削阻力切向分力计算结果与实测值的对比如图10所示。

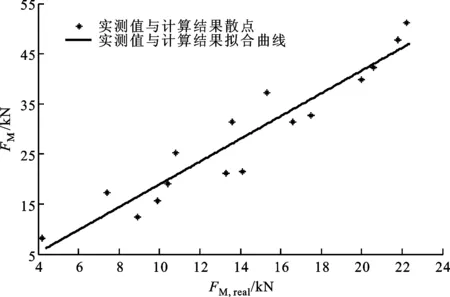
图10 多刀铣削阻力切向分力的计算结果与实测值

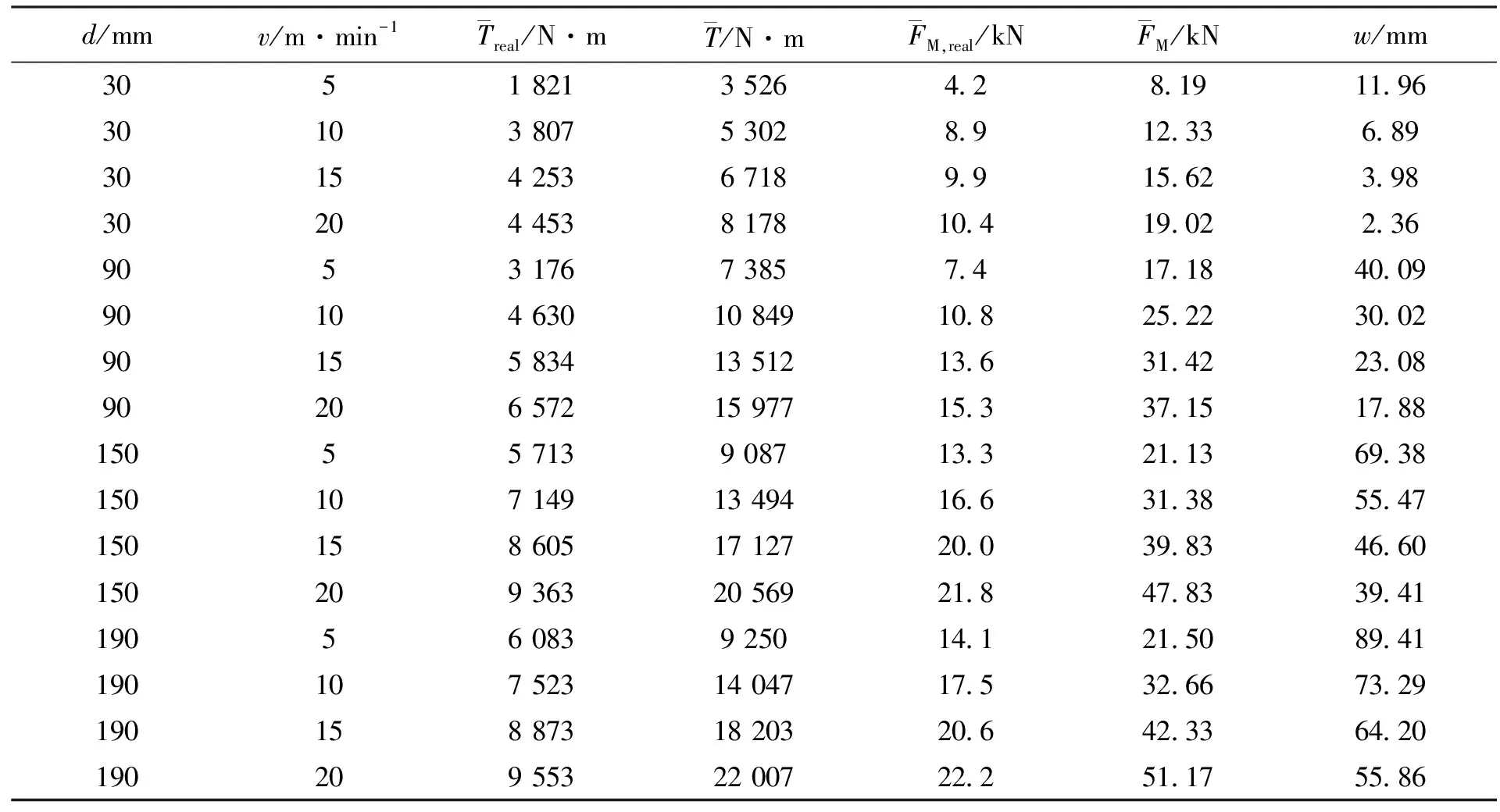
d/mmv/m·min-1Treal/N·mT/N·mFM，real/kNFM/kNw/mm3051821352642819119630103807530289123368930154253671899156239830204453817810419022369053176738574171840099010463010849108252230029015583413512136314223089020657215977153371517881505571390871332113693815010714913494166313855471501586051712720039834660150209363205692184783394119056083925014121508941190107523140471753266732919015887318203206423364201902095532200722251175586

由图10可知,旋转多刀铣削阻力切向分力的实测值FM,real与计算值FM线性相关,相关系数为0.90,线性回归方程为

FM,real=0.396FM+2.912

(19)

理论计算能够反映铣刨机实际作业过程中不同铣削深度和工作速度下多刀铣削阻力切向分力的变化,但是理论计算值大于同工况下的实测值。参照式(16)、式(19)进行修正后,旋转多刀铣削阻力切向分力的计算公式变为

FM=0.396cos(φ+β)∑F+2.912=

(20)

编制程序确定各参数后,可按式(20)进行旋转多刀铣削阻力切向分力的计算。

旋转多刀铣削阻力切向分力实测值与计算值之间的误差来源于:①多刀铣削阻力计算模型中未考虑到多刀具联合铣削作用时大块径废料比例增大、单刀实际铣削阻力减小;②刀具在铣削厚度较大时计入的接触面截面积S偏大,而实际刀具与沥青混凝土的接触面为碳化钨刀尖区域,主要是铣屑长度l的变化,但l无法量化;③单刀铣削由于边界条件限制,不能实现与多刀铣削等深度的铣削,因此采用单刀铣削阻力修正公式计算多刀铣削阻力会带来误差;④刀具排布的简化以及路面材料破坏强度不同会带来误差;⑤多刀铣削转子驱动扭矩实测中不计空转驱动扭矩、忽略转子惯性对铣削过程的作用以及铣削转子传动效率取固定值也会带来误差。以上原因导致多刀铣削阻力的计算值大于同工况下的实测值,因此,单刀铣削阻力的理论计算方法还需通过进一步试验以实现与多刀铣削等同深度的铣削,并通过加入更详细的刀具排布参数、直接在铣削转子传动轴测量扭矩以得到更准确的驱动扭矩数据、确定旋转多刀铣削阻力计算公式修正系数等方法,以提高旋转多刀铣削阻力计算的准确性和适用范围。

5 结 论

(1)将单刀旋转变厚度铣削在任意瞬时近似为以刀尖点切线速度为进给速度的等厚度平移切削,以剪切变形破坏得到了单刀铣削阻力计算方法,并以铣削接触面截面积为自变量进行了单刀铣削阻力计算公式的修正;将任一时刻处于不同铣削位置的各刀具的铣削阻力向量叠加作为旋转多刀铣削阻力,得到了旋转多刀铣削阻力切向分力和驱动扭矩的计算公式。

(2)某1 m铣刨机在不同工况下的旋转多刀铣削阻力切向分力的理论计算值与实测值线性相关,理论计算能够反映铣刨机实际作业过程中的铣削阻力变化,但计算值大于同工况下的实测值。

(3)沥青混凝土旋转多刀铣削阻力的数值计算方法为旋转类多刀具切削阻力计算提供了思路。要使理论计算值更加接近实测数据,需考虑刀具作用过程中的实际接触长度、实际接触面与理论计算中的差异,以及单刀具长弧段铣削轨迹中刀具的渐进冲击破坏特性与理论计算中连续铣屑的差异,还必须考虑多刀具同时参与铣削时刀具间的相互作用和刀具排布参数,以便能更准确地反映铣削载荷的波动。需进行单刀与多刀等同铣削深度试验,以便更准确地修正单刀铣削阻力计算公式,并扩大试验范围,对沥青混凝土材料、刀具结构、刀具排布、铣削作业速度、铣削转子转速、铣削圆半径、铣削深度、铣削宽度等因素选取不同水平进行单因素、多因素试验,从而修正多刀铣削阻力计算模型。在数值计算的基础上,进一步简化模型,得到多刀旋转铣削阻力的解析计算方法,以便应用于工程实际。

[1] 曾卫兵, 赵敏, 何挺继. 沥青路面铣刨机作业性能分析与验证 [J]. 长安大学学报(自然科学版), 2004, 24(3): 58-61. ZENG Wei-bing, ZHAO Min, HE Ting-ji. Working performance for asphalt road plane milling machine [J]. Journal of Chang’an University (Natural Science Edition), 2004, 24(3): 58-61.

[2] 顾海荣, 焦生杰, 肖翀宇, 等. 路面铣刨机铣削载荷特性分析与试验 [J]. 中国公路学报, 2012, 25(3): 154-158. GU Hai-rong, JIAO Sheng-jie, XIAO Chong-yu, et al. Analysis and test on asphalt milling machine cutting load characteristic [J]. China Journal of Highway & Transport, 2012, 25(3): 154-158.

[3] 田晋跃, 向华荣. 路面铣刨机铣削阻力及其参数影响规律分析 [J]. 江苏大学学报(自然科学版), 2004, 25(5): 380-384. TIAN Jin-yue, XIANG Hua-rong. Analysis on parameter influence laws and milling resistances of pavement miller [J]. Journal of Jiangsu University (Natural Science Edition), 2004, 25(5): 380-384.

[4] 吕聪正. 路面铣刨机铣刨系统分析与优化设计 [D]. 西安: 长安大学, 2014.

[5] DAVE E V, BEHNIA B, AHMED S, et al. Low temperature fracture evaluation of asphalt mixtures using mechanical testing and acoustic emissions techniques [J]. Journal of the Association of Asphalt Paving Technologists, 2011, 80(4): 193-226.

[6] HAKIMZADEH S, BUTTLAR W, SANTARROMANA R. Shear- and tension-type tests to evaluate bonding of hot-mix asphalt layers with different tack coat application rates [J]. Journal of the Transportation Research Board, 2012, 10(2295): 54-62.

[7] TOZZO C, D’ANDREA A, COZZANI D, et al. Fatigue Investigation of the interface shear performance in asphalt pavement [J]. Modern Applied Science, 2014, 8(2): 1-11.

[8] 高相斌, 赵伟民, 胡长胜, 等. 点式冲击刀具的理论与实验分析 [J]. 哈尔滨工业大学学报, 2003, 35(6): 755-760. GAO Xiang-bin, ZHAO Wei-min, HU Chang-sheng, et al. Theoretical and test analysis of point attach bit [J]. Journal of Harbin Institute of Technology, 2003, 35(6): 755-760.

[9] DOGRUOZ C, BOLUKBASI N, ROSTAMI J, et al. An experimental study of cutting performances of worn picks [J]. Rock Mechanics and Rock Engineering, 2016, 49(1): 213-224.

[10]CHEREPANOV G P. Theory of rock cutting [J]. Strength of Materials, 1986, 18(8): 1103-1114.

[11]SU O, AKCIN N A. Numerical simulation of rock cutting using the discrete element method [J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48(3): 434-442.

[12]NISHIMATSU Y. The mechanics of rock cutting [J]. International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts, 1972, 9(2): 261-270.

[13]魏春景. 沥青路面冷铣刨机工作过程的动力学研究 [D]. 西安: 长安大学, 1995: 58-59.

[14]吕聪正, 冯忠绪, 李耀, 等. 铣刨机行驶作业阻力特性分析 [J]. 山东交通学院学报, 2013, 21(2): 74-76. LÜ Cong-zheng, FENG Zhong-xu, LI Yao, et al. Study on running resistance characteristics of asphalt milling machine [J]. Journal of Shandong Jiaotong University, 2013, 21(2): 74-76.

[本刊相关文献链接]

高羡明,洪军,甄宜超.机床多体系统空间刚度场约束下的加工误差预测.2016,50(6):90-96.[doi:10.7652/xjtuxb201606 014]

潘俊浩,卓勇,连云崧,等.硬质合金内冷钻头三维参数化建模研究.2015,49(10):48-53.[doi:10.7652/xjtuxb201510 008]

朱爱斌,胡浩强,何大勇,等.采用频域融合方法的砂轮刀具磨损三维重构技术.2015,49(5):82-86.[doi:10.7652/xjtuxb 201505013]

耿麒,魏正英,孟昊,等.TBM的平面刀盘与两级刀盘的力学性能对比分析.2015,49(3):121-128.[doi:10.7652/xjtuxb 201503019]

周光辉,苗发祥,李彦广.数控加工中心任务与刀具集成调度模型及改进自适应遗传算法.2014,48(12):1-7.[doi:10. 7652/xjtuxb201412001]

耿麒,魏正英,杜军.全断面岩石掘进机滚刀布置的优化方法.2013,47(9):100-105.[doi:10.7652/xjtuxb201309017]

王建录,成冰,赵万华,等.汽轮机长叶片型面双刀加工刀位轨迹优化算法.2013,47(9):65-71.[doi:10.7652/xjtuxb 201309011]

章云,梅雪松,胡振邦,等.注液式高速切削主轴动平衡装置设计及其性能研究.2013,47(3):13-17.[doi:10.7652/xjtuxb 201303003]

黄泽华,李建勇,樊文刚,等.复杂曲面薄壁叶片点铣加工弹性变形预测.2012,46(5):67-72.[doi:10.7652/xjtuxb2012 05012]

樊文刚,李建勇,黄泽华,等.多点切触加工在复杂凸曲面中的应用.2012,46(3):53-57.[doi:10.7652/xjtuxb201203 010]

赵鹏,楼佩煌,刘明灯,等.实轴空间综合约束下的数控加工速度前瞻策略.2012,46(2):64-69.[doi:10.7652/xjtuxb 201202011]

樊文刚,李建勇,蔡永林,等.复杂曲面多点切触加工特征参数线刀轨规划.2012,46(1):81-85.[doi:10.7652/xjtuxb 201201015]

吕凯波,景敏卿,张永强,等.一种切削颤振监测技术的研究与实现.2011,45(11):95-99.[doi:10.7652/xjtuxb201111 018]

孙殿柱,康新才,李延瑞,等.三角Bézier曲面粗加工刀轨生成算法.2011,45(3):70-74.[doi:10.7652/xjtuxb201103013]

樊文刚,王小椿,姜虹,等.一种开阔自由凹曲面五坐标加工多点刀位算法.2010,44(9):69-73.[doi:10.7652/xjtuxb 201009014]

邱昕洋,张光辉,秦大同.平面蜗轮连续分度飞削加工及工艺试验研究.2010,44(7):95-99.[doi:10.7652/xjtuxb201007 021]

张润理,鲍崇高.系列α-Al2O3结构陶瓷的耐冲蚀磨损性能.2010,44(5):71-74.[doi:10.7652/xjtuxb201005015]

(编辑 葛赵青)

Numerical Calculation on Multi-Tool Milling Resistance of Asphalt Pavement Milling Machine

WANG Xuebin,HU Yongbiao

(Key Laboratory for Highway Construction Technology and Equipment of Ministry of Education,Chang’an University, Xi’an 710064, China)

To calculate the multi-tool milling resistance of asphalt pavement milling machine and transform any instantaneous milling process of rotating single tool into a uniform-thickness translation cutting with the tangential velocity of tool nose, a calculation model of single-tool milling resistance is established based on shear failure. Multi-tool milling resistance is the vector sum of each tool’s milling resistance at any given time, and the numerical calculation method of the tangential component force of multi-tool milling resistance is obtained. The calculation formula for single-tool milling resistance is modified with the sectional area of milling contact as the independent variable. The theoretical value and measured data of an experimental prototype milling machine are compared, and the results show that their linear correlation coefficientR2is 0.9. The calculation formula for tangential component force of multi-tool milling resistance is modified based on the measured data, and the error source is analyzed. The calculation model may provide a reference for calculation of single- and multi-tool cutting resistances.

asphalt pavement milling machine; milling resistance; multi-tool milling; numerical calculation

2015-12-01。 作者简介:汪学斌(1986—),男,博士生;胡永彪(通信作者),男,教授。 基金项目:中央高校基本科研业务费专项资金资助项目(CHD2011TD016,310825153313);国家科技支撑计划资助项目(2011BAE28B03)。

时间:2016-04-28

10.7652/xjtuxb201607015

U415.5

A

0253-987X(2016)07-0096-08

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20160428.2222.006.html